三、动态最优（I）拉格朗日方法

樊潇彦 复旦大学经济学院 数量经济学

0. 准备工作

setwd("D:\\...")   # 设定工作目录
rm(list=ls())      # 清内存
# "Ctrl"+"L" 清除命令窗口

1. 生命周期储蓄问题：射击方法求解

T=10; 
k0=kT=0
w=1
beta=0.95
R=1/beta+c(0.1,0,-0.1)                 # 比较三种beta*R的情况，利率 R=1+r
dim1=c("c","k")                        # 把结果存为3维数组x，行为变量名 c,k
dim2=c(1:T)                            # 列为时间 1,2...T
dim3=paste("beta*R=",round(beta*R,2))  # 高为 beta*R 的三种情况
x=array(rep(NaN,2*T*length(R)),
        c(2,T,length(R)),
        dimnames=list(dim1,dim2,dim3)) 
tol=0.00001;                           # 循环的参数设置
maxloop=100; 
par(mfrow=c(length(R),1))              # 做图窗口，3张图
for (case in 1:length(R)){             # 分情况搜索的循环  
  Phi = matrix(c(beta*R[case],-1,0,R[case]),2,2)
  c_max=w/(1/beta-1)                   # 猜测区间。c_max > w 允许负债 k<0
  c_min=0.01                           # c_min > 0
  error=2*tol; loop=0
  while (error>tol & loop<maxloop){   
    c_guess=(c_min+c_max)/2              # c 的初始猜测                    
    c=rep(c_guess,T)                     # 初始化路径
    k=rep(k0,T) 
    x[,,case]=rbind(c,k)
    for (t in 2:T){                      # 更新路径
      x[,t,case]=Phi %*% matrix(x[,t-1,case]) +c(0,w)
    }
    if (x[2,T,case]<kT){                 # 判断初始猜测是否过高 
      c_max=c_guess                      # 调低上限
    } else
    {
      c_min=c_guess                      # 调高下限
    }  
    error= abs(x[2,T,case]-kT)           # 用于决断是否收敛
    loop=loop+1   
  }
  matplot(t(x[,,case]),col=c("red","blue"),type="l", ylim=range(-2,2), main=dim3[case], ylab="")
}

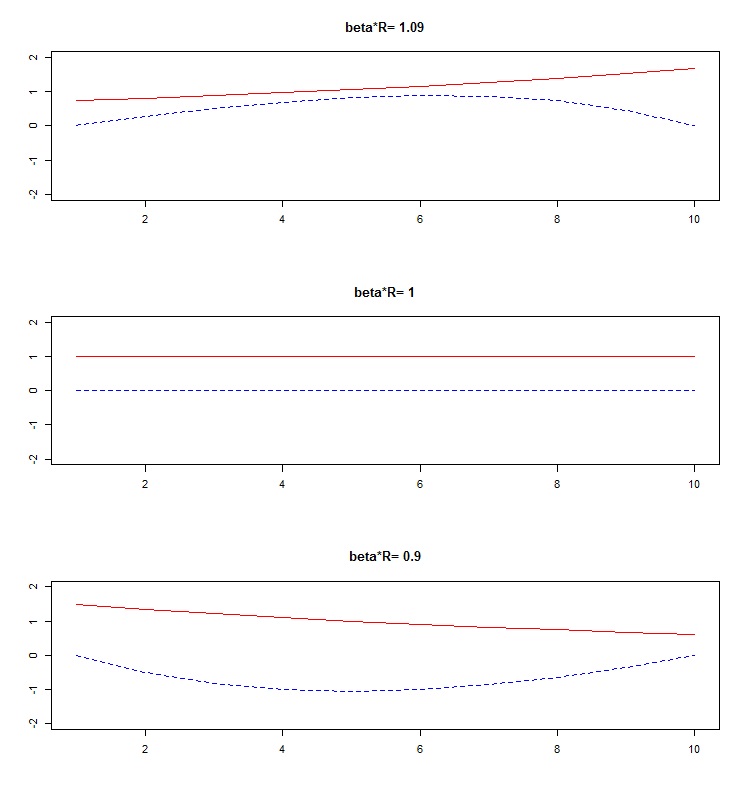
2. 最优增长问题

2.1 设置参数

T=20
beta=0.95; gamma=1
z=5; alpha=0.4; delta=1
kstar=(alpha*z/(1/beta+delta-1))^(1/(1-alpha))       # 稳态
cstar=((1/beta+delta-1)/alpha-delta)*kstar
casetype=c(0.5,1.5)
k0vector=kstar*casetype                              # 两种初始k0
tol=0.0001;                                          # 循环的参数设置
maxloop=100; 
datax=data.frame()                                   # 准备存放数据

2.2 搜索最优路径

for (case in 1:length(k0vector)){
  k0=k0vector[case]
  c_max=z*k0^alpha+(1-delta)*k0-0.01             # 生产函数要求 k_t+1 > 0，构成c的上限
  c_min=0.01                                     # c > 0
  error=2*tol; loop=0
  while (error>tol & loop<maxloop){   
    c_guess=(c_min+c_max)/2                      # c 的初始猜测                    
    c=rep(c_guess,T)                             # 初始化路径
    k=rep(k0,T) 
    for (t in 2:T){                              # 更新路径
      c[t]=c[t-1]*(beta*(alpha*z*k[t-1]^(alpha-1)+1-delta))^(1/gamma)
      k[t]=z*k[t-1]^alpha+(1-delta)*k[t-1]-c[t]
      if (c[t]>c[t-1]& k[t]<k[t-1]){             # 判断初始猜测是否过高 
        c_max=c_guess                            # 落入左上区域，调低上限
        break}                                   # 中止循环
      else if (c[t]<c[t-1] & k[t]>k[t-1]){
        c_min=c_guess                            # 落入右下区域，调高下限
        break                                    # 中止循环
      }          
    }
    if (t==T & k[T]<kstar){                      # 判断初始猜测是否过高 
      c_max=c_guess                              # 调低上限
      error= abs(k[T]-kstar)                     # 用于决断是否收敛
    } else if (t==T & k[T]>kstar){
      c_min=c_guess                              # 调高下限
      error= abs(k[T]-kstar)                     # 用于决断是否收敛
    } # end of for()
    loop=loop+1   
  } # end of while() for shooting
  x=data.frame(c,k,rep(cstar,T),rep(kstar,T))
  datax=rbind(datax,x)
  matplot(as.matrix(x), type="l",col=c("red","blue","pink","green"),main=paste("c_t and k_t with k0=",casetype[case],"*kstar"))
  legend("bottomright",c("c_t","k_t","cstar","kstar"),col=c("red","blue","pink","green"),lty=1)
} # end of grid of k0vector

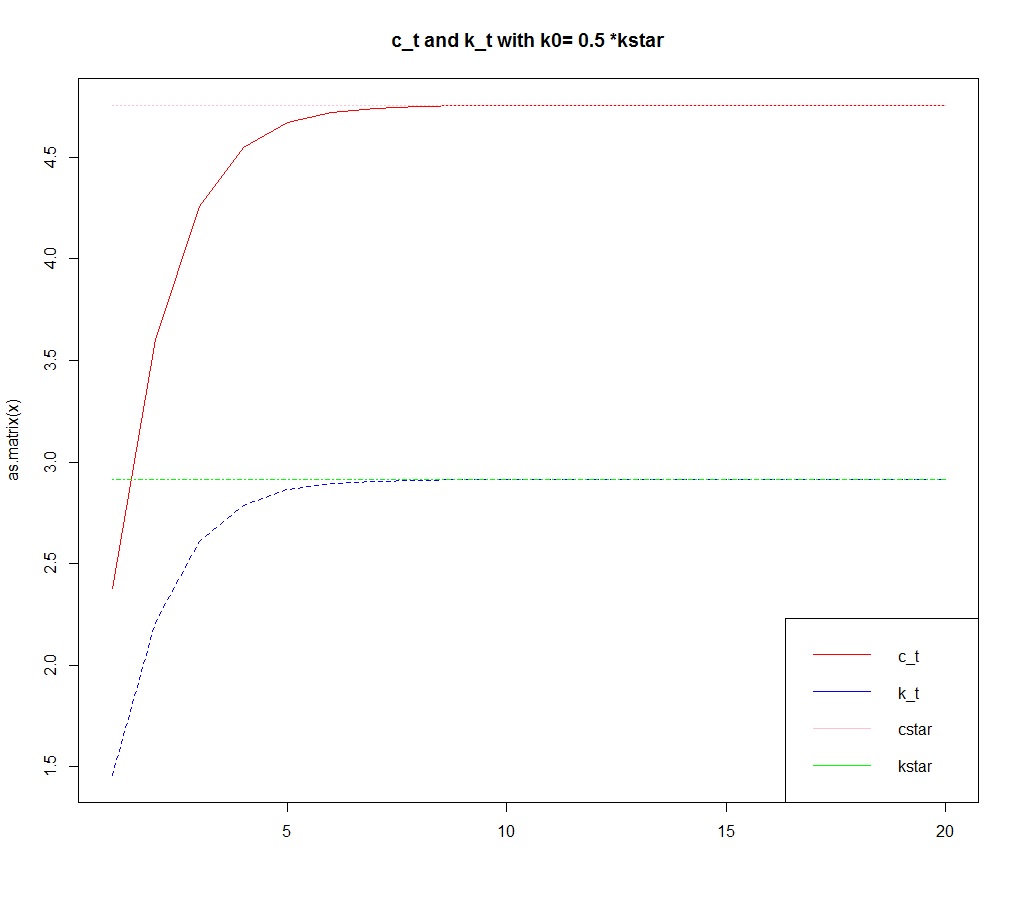
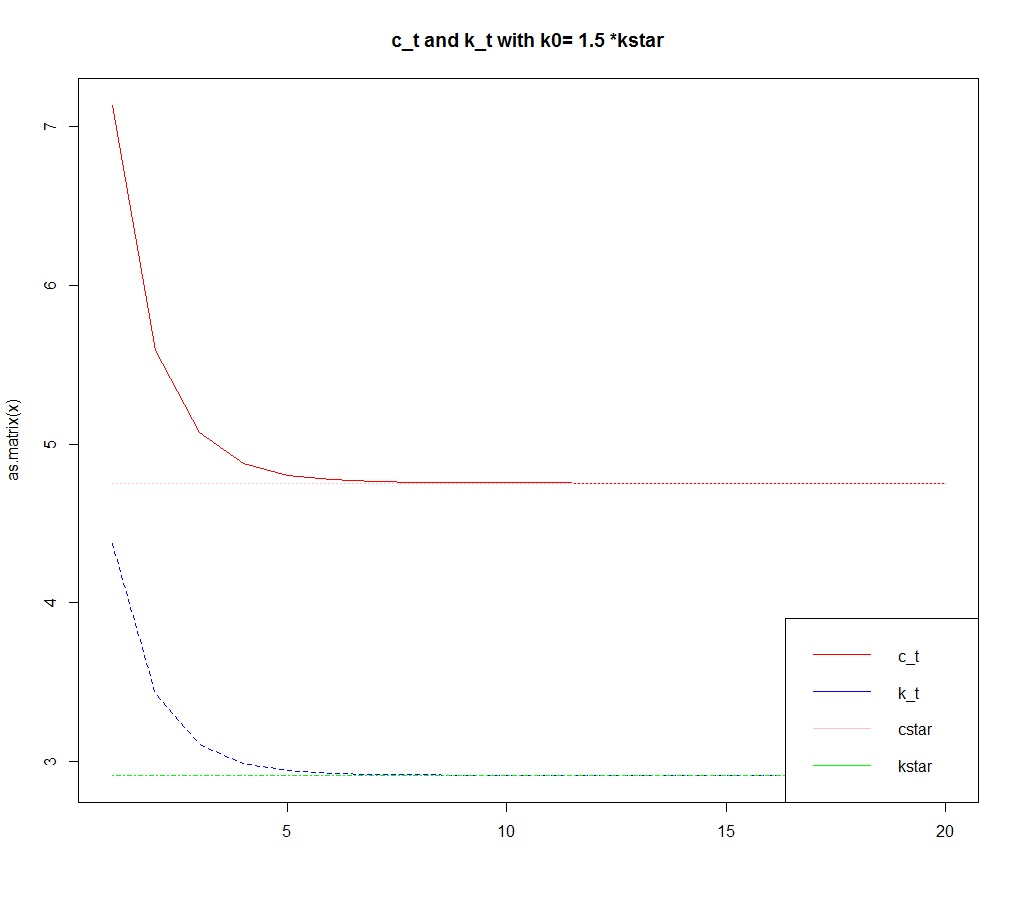
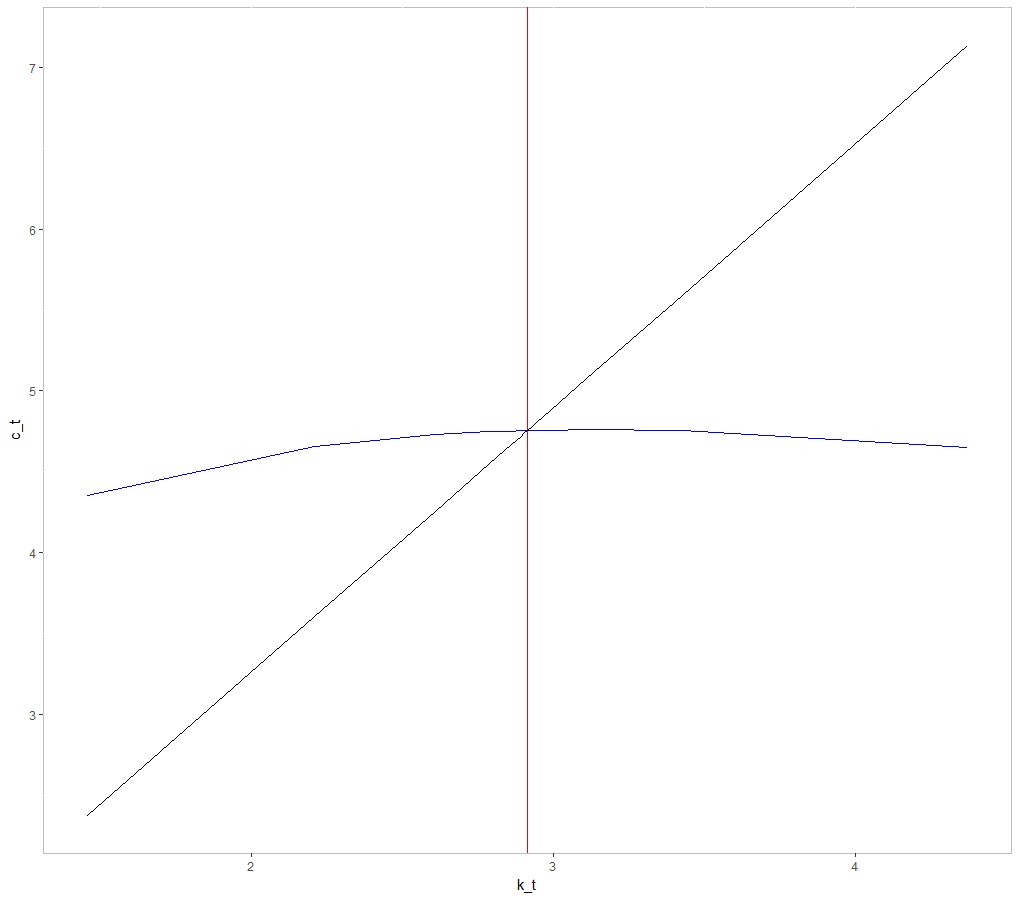
2.3 绘制相图

datax$kss=z*datax$k^alpha-delta*datax$k
library(ggplot2)
ggplot(data=datax,legend=TRUE) +
  geom_vline(xintercept=kstar,colour="red") +
  geom_line(aes(x=k,y=kss),colour="blue") +
  geom_line(aes(x=k,y=c),colour="black") +
  ylab("c_t") + xlab("k_t") +  xlim(k0vector) + 
  theme(panel.background=element_rect(fill='transparent', color='gray'))