第九讲 非平稳时间序列线性模型

樊潇彦 复旦大学经济学院 金融数据

---

Ch09_Data.rar412.8kB

# 准备工作
setwd("D:\\...\\Ch09")
install.packages("fracdiff")
library(tidyverse)
library(readxl)
library(ggplot2)
library(tseries)
library(zoo)
library(forecast)

1. 随机游走

1.1 定义与数值模拟

• 单位根非平稳时间序列（以股票的对数价格为例）：
  $$p_t = p_{t-1} + \varepsilon_t$$
• 带漂移的随机游走过程（截距项为序列的时间斜率）：
  $${p_t} = \mu + {p_{t - 1}} + {\varepsilon _t} = t\mu + {p_0} + \sum\limits_{s = 1}^t {{\varepsilon _s}}$$

source("Ch09_myfun.R")                              # 调用函数
set.seed(2)                                         # 设定随机种子
simu_random(mu=0, sigma=1, T=100, N=50)             # 运行
# mu: shift;    sigma: sd(epsilon)
# T：模拟T期;   N: 模拟N次

1.2 标普500指数建模

sp=read.table("d-sp5008.txt",header=T)                    # 读取SP500数据
head(sp)
lnp=ts(log(sp$close),start=c(1950,1,3))                   # 取收盘价对数，转换为ts对象
adf.test(lnp)                                             # ADF检验，H0:有单位根
regsp=auto.arima(lnp,stationary = F, seasonal = F, ic="aic") 
regsp
par(mfcol=c(1,1))
plot(regsp$x,lty = 1, main = "拟合S&P500指数", ylab = "", xlab = "")
lines(fitted(regsp), lty = 2,lwd = 2, col = "red")
head(data.frame(regsp$x,fitted(regsp)))                   # 比较真实数据和拟合结果

2. 季节模型

2.1 直接用auto.arima()命令建模分析

下面以可口可乐公司的财务数据为例，展示如何用auto.arima()命令进行建模分析。

da=read.table("q-ko-earns8309.txt",header=T)$value        # 读取数据
koeps=ts(log(da),frequency=4,start=c(1983,1))             # 将对数值转换为ts对象
par(mfcol=c(1,1))  
plot(koeps,type='l')                                      # 作图
points(koeps,pch=c("1","2","3","4"),cex=0.6)              # 标记季度
adf.test(koeps)                                           # ADF检验，H0:有单位根
regkoeps = auto.arima(koeps,stationary = F, seasonal = T, ic="aic")
regkoeps
tsdiag(regkoeps)
par(mfcol=c(2,1))  
plot(regkoeps$x,lty = 1, main = "盈利拟合", ylab = "", xlab = "")
lines(fitted(regkoeps), lty = 2,lwd = 2, col = "red")
plot(forecast(regkoeps), main = "盈利预测")
predict(regkoeps, n.ahead=4)                              

2.2 数据分解和季节调整后建模分析

有的数据用auto.arima()回归后残差仍存在自相关，或存在明显的季节性波动，回归结果不理想。以1992Q1-2016Q4的中国季度GDP数据为例：

load("ydata.RData")                                       # 读取数据
head(ydata)
reglny=auto.arima(ydata$lny, stationary = F, seasonal = T, ic="aic")
reglny
tsdiag(reglny)                                            # 作图观察
Box.test(reglny$residuals,lag=4,type='Ljung')             # 序列自相关检验

对于这种情况，可以用基础stats包中的decompose()命令先对原始数据进行分解，生成经季节调整的数据后再建模。

lny=ts(ydata$lny,frequency=4, start=c(1992,1))            # 转换为ts对象
lny_dec=stats::decompose(lny)                             # 分解为趋势、季节和随机因素
plot(lny_dec)                                             # 分解结果作图
lny_adj=seasadj(lny_dec)                                  # 生成经季节调整的数据
par(mfcol=c(1,1))  
plot(lny)                                                 # 比较季节调整前后的数据
lines(lny_adj, col="red")
reglny_adj=auto.arima(lny_adj, stationary =F, seasonal = F,  ic="aic")
reglny_adj
tsdiag(reglny_adj)
Box.test(reglny_adj$residuals,lag=4,type='Ljung')  
par(mfcol=c(2,1))  
plot(reglny_adj$x,lty = 1, main = "lny_adj拟合", ylab = "", xlab = "")
lines(fitted(reglny_adj), lty = 2,lwd = 2, col = "red")
predict(reglny_adj, n.ahead=4)
plot(forecast(reglny_adj), main = "lny_adj预测")

课堂讨论：改用上一讲1992Q1-2019Q4的中国季度GDP数据（CME_Qqgdp.xls）重新分析，结果是否有变化？

3. 协整检验与误差修正模型

3.1 协整（cointegration）检验

• 定义：如果两个（或多个）非平稳的时间序列通过线性组合，可以得到平稳的时间序列，则称其存在协整关系。

• 恩格尔-格兰杰两步检验法（Engle–Granger two-step method）：

  • OLS回归：
    $$y_t = \beta_0 + \beta_1 x_t + \varepsilon_t$$
  • 检验 $\hat \varepsilon_t = y_t -\hat \beta_0 -\hat \beta_1 x_t$ 的平稳性。平稳说明 $y_t,~x_t$ 之间存在协整关系。

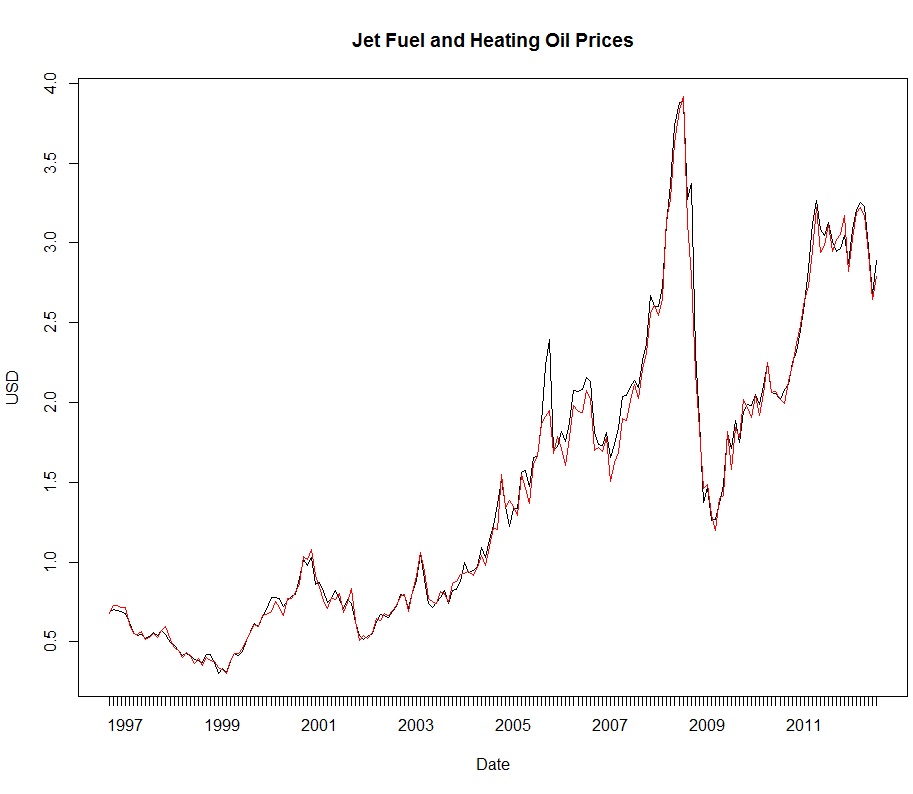
• 示例：两种油价的协整关系

# 数据读入并作图
oil <- read.zoo("JetFuelHedging.csv", sep = ",", FUN = as.yearmon, format = "%Y-%m", header = TRUE)    
par(mfcol=c(1,1))
plot(oil$JetFuel, main = "Jet Fuel and Heating Oil Prices")    
lines(oil$HeatingOil, col = "red")
legend("topleft", c("-- Jet Fuel","-- HeatingOil"), 
       bty="n", text.col = c("black","red"))
# OLS回归，残差平稳
lmoil <- lm(oil$JetFuel ~ oil$HeatingOil)
summary(lmoil) 
par(mfcol=c(2,1))
plot(lmoil$residuals)
acf(lmoil$residuals,lag=12)
adf.test(lmoil$residuals)

3.2 误差修正模型（Error correction model，ECM）

Engle and Granger(1987) 指出如果非平稳变量 $y_t,~x_t$ 是协整的，则存在下述误差修正模型：

$$A(L) \Delta y_t = \alpha + B(L)\Delta x_t + \gamma \hat \varepsilon_t + \Theta(L) u_t$$

以美国1年期和3年期两种国债的收益率为例，直接回归下述方程得到的残差 $\varepsilon_t$ 是非平稳的：

$$r_{3t} = \beta_0 + \beta_1 r_{1t} + \varepsilon_t$$

# 数据读入并作图
r1=read.table("w-gs1yr.txt",header=T)
r3=read.table("w-gs3yr.txt",header=T)
time=paste(r1$year,r1$mon,r1$day,sep="-")
r=data.frame(time=as.Date(time,format="%Y-%m-%d"),
             r1=r1[,4],r3=r3[,4])
head(r)
r$yymm=as.yearmon(r$time)
matplot(x=r$yymm,r[,2:3],type="l",xlab="",ylab="",main="1年期和3年期美国国债利率（%）")
legend(x=1990, y=15, horiz = F, legend=c("1年期","3年期"), lty=1:2, bty="n",
       box.lty=0, col=c("black","red"))
# P85, (2-46)式OLS回归，残差非平稳
m1=lm(r3~r1,data=r)
summary(m1)
acf(m1$residuals,lag=12)

根据Tsay(2015)，回归下述EMC模型得到平稳残差，表明两种利率之间存在协整关系：

$$\Delta r_{3t} = \Delta r_{1t} + u_t - \theta_1 u_{t-1}$$

# P88, (2-49)式回归
c1=diff(r$r1)
c3=diff(r$r3)
m3=arima(c3,order=c(0,0,1),xreg=c1,include.mean=F)
m3
tsdiag(m3)
# 与下面的命令结果一致
auto.arima(r$r3,stationary=F, seasonal=F, xreg=r$r1, ic="bic")

3.3 应用：配对交易策略

如果两支股票的对数价格存在以下协整关系：

$$p^y_t = \alpha + \gamma p^x_t + \varepsilon_t$$

则通过构造一个线性资产组合 $z = y-\gamma x$ 就可以获得平稳收益 $\Delta \varepsilon_t$：

$$r^z_t = r^y_t - \gamma r^x_t = \Delta p^y_t - \gamma \Delta p^x_t = \Delta \varepsilon_t$$

一个简单的交易策略为：
1. 假定 $t$ 期 $p^y_t - \gamma p^x_t = \delta >0$，说明 $y$ 的价格相对于 $x$ 被高估，可以在远期市场卖出1单位 $y$ 的同时买入 $\gamma$ 单位 $x$，资产组合的潜在价值为 $\delta$；
2. 假定 $s>t$ 期$p^y_s - \gamma p^x_s =0$，即 $y$ 相对于 $x$ 出现价格回落，此时从市场上买入1单位 $y$ 、同时卖出 $\gamma$ 单位 $x$，完成远期合约交割后得到收益 $\delta$。

只要 $\delta$ 大于交易费用和风险因素等构成的交易成本，就可以通过上述策略获得稳定收益。

课堂讨论：澳大利亚的BHP和巴西的VALE是两家自然资源行业的公司，请以其2002年7月1日到2006年3月31日的数据为例，构造交易策略。

# 读入数据并作图
da=read.table("d-bhp0206.txt",header=T)
da1=read.table("d-vale0206.txt",header=T)
bhp=log(da$adjclose)
vale=log(da1$adjclose)
matplot(data.frame(bhp,vale),type='l')
# OLS估计
regols=lm(bhp~vale)
summary(regols)
acf(regols$residuals)                        # 残差自相关
# EMC模型
regemc=auto.arima(bhp,stationary=F, seasonal=F, xreg=vale, ic="aic")
regemc                                        
tsdiag(regemc)                               # 回归结果理想，存在协整关系

4. 其他常用模型

4.1 指数平滑

假设时间序列$x_t$的序列相关性以指数衰减，其中$\omega \in \left(0,1\right)$是贴现因子：

$$\hat x_{t+1} \propto \omega x_t + \omega^2 x_{t-1} + ... = \sum_{s=1}^{+\infty}{\omega^sx_{t+1-s}}$$
这种预测方法叫做指数平滑法（exponential smoothing method），是ARIMA(0,1,1)模型的特殊情形（详见Tsay(2015)第2.8节）。

# P73-74：
da=read.table("d-vix0810.txt",header=T)
vix=log(da$Close)
m1=arima(vix,order=c(0,1,1))
m1
# stats包中命令回归，结果一样：
vix_holt=HoltWinters(vix, beta=F, gamma=F)
vix_holt$alpha-1

4.2 长记忆（AFRIMA）模型

如果一个时间序列的样本ACF在数值上不大，但衰减得很慢，则该序列可能有长记忆。考虑估计以下模型：

$$(1-L)^d y_t =\varepsilon_t,~~-0.5<d<0.5$$

library(fracdiff)
da=read.table("d-ibm3dx7008.txt",header=T)
ew=abs(da$vwretd)
fdGPH(ew)$d                            # Geweke-Port-Hudak方法估计d
summary(fracdiff(ew,nar=1,nma=1))      # 估计AFRIMA(1,d,1)模型

4.3 模型选择

在auto.arima()等命令中，可以选择常用的模型选择标准ic=c("aicc", "aic", "bic")。此外还可以通过forecast::accuracy()命令报告的指标，比较不同模型的回归精度，如：
- ME: Mean Error
- RMSE: Root Mean Squared Error
- MAE: Mean Absolute Error
- MPE: Mean Percentage Error
- MAPE: Mean Absolute Percentage Error
- MASE: Mean Absolute Scaled Error
- ACF1: Autocorrelation of errors at lag 1.

accuracy(reglny)

参考文献

• Daroczi, C. et al. 2013: Introduction to R for Quantitative Finance, Packt Publishing Ltd.
• Tsay, R.S. 2013：《金融时间序列分析（第3版）》，王远林、王辉、潘家柱译，人民邮电出版社