@fanxy 2020-03-12T10:34:34.000000Z 字数 5439 阅读 4368

一、静态最优数学基础

樊潇彦 复旦大学经济学院 数量经济学

一、静态最优数学基础
准备工作
1. 微积分
- 1.1 最优投资组合
- 1.2 消费者最优
2. 线性代数
3. 统计与计量
- 3.1 《定价未来》
- 3.2 用 lm() 做OLS回归
4. 数据与软件
- 4.1 数据来源
- 4.2 软件资料

准备工作

setwd("D:\\...")               # 设定工作目录
rm(list=ls())
# 安装程序包
install.packages("Rsolnp")     # 非线性最优
install.packages("ggplot2")    # 作图

# 调用
library(Rsolnp)
library(ggplot2)

1. 微积分

1.1 最优投资组合

$\mathop {Max}\limits_\theta U = \theta\mu + (1-\theta)r_f - \frac{1}{2}A{\theta^2}\sigma^2\\ \Rightarrow \theta=\frac{\mu -r_f}{A\sigma^2}$

# 作图
mu=0.1; r_f = 0.02; A =10; sigma=0.2
theta= seq(0,1, by=0.05)
U = theta*mu + (1-theta)*r_f - A*theta^2*sigma^2/2
data=data.frame(theta, U)
ggplot(data) +
  geom_line(aes(x=theta, y=U)) +
  geom_vline(xintercept=(mu-r_f)/A/sigma^2, color="red") +
  labs(x="风险资产占比", y="效用") +
  theme_bw()
# 求解
theta0=0.01; LB=0; UB=1                    # 参数初始值、下限和上限
U_fun=function(theta){                     # 目标函数
  U=theta*mu + (1-theta)*r_f - A*theta^2*sigma^2/2
  return(-U)                               # 默认为最小化，加负号改为最大化
}
-U_fun(0.2)                                # 当theta=0.2时，计算效用值                  
UMP=solnp(theta0, fun=U_fun, LB=LB, UB=UB) # 求解消费者最优化问题   
result=data.frame(theta=UMP$pars,maxU=-tail(UMP$values,1),SOC=UMP$hessian)
round(result,3)                            # 保留小数点后3位，显示最优化结果

1.2 消费者最优

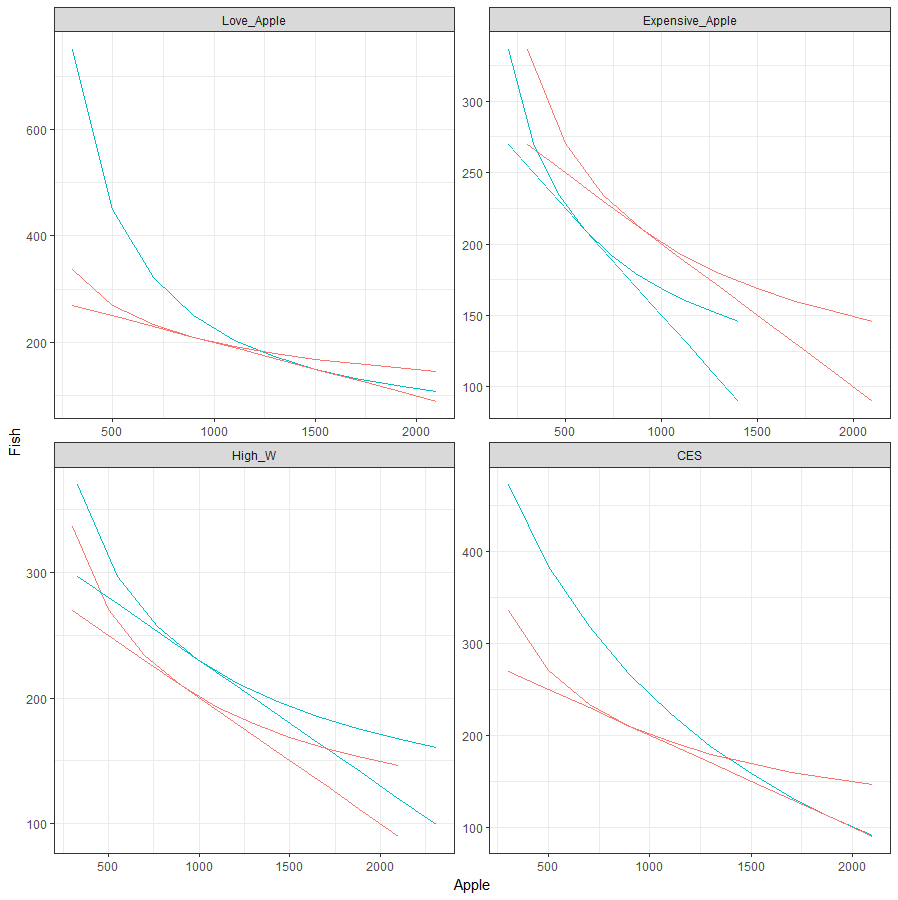
## 第1步：函数设定
U_fun=function(c){
  if (rho==0) {U=(c[1])^alpha*(c[2])^(1-alpha)}else{
    U=(alpha*(c[1])^rho+(1-alpha)*(c[2])^rho)^(1/rho)    # 最大化效用
  }
  return(-U)   # min_(-U)                                # 默认为最小化目标函数
}
budget=function(c){p1*c[1]+p2*c[2]}                      # 预算约束方程
c2_u0=function(c2,alpha,rho,c1,maxU0){                   # 给定U0和c1求c2，用于画无差异曲线
  if (rho==0){log(maxU0)-( alpha*log(c1)+(1-alpha)*log(c2) )}else log(maxU0)-1/rho*log(alpha*c1^rho+(1-alpha)*c2^rho)
} 
## 第2步：分不同情况求解
fig_data=result=data.frame()                                    # 准备存放作图的数据
for (case in c("Basic","Love_Apple","Expensive_Apple","High_W","CES")){ # 分四种情况 
  p1=0.1; p2=1; w=300;                                                  # 外生变量
  alpha=0.3; sigma=1; rho=1-1/sigma                                     # 模型参数
  switch(case,
         "Love_Apple"={
           alpha=0.5      
         },
         "Expensive_Apple"={
           p1=0.15
         },
         "High_W"={
           w=330
         },
         "CES"={
           sigma=2; rho=1-1/sigma       
         })
  maxc1=w/p1; maxc2=w/p2 
  # 给定预算约束，求解消费者最优化问题
  find_cstar=solnp(c(maxc1/2,maxc2/2),                # 初始猜测
              fun=U_fun,                              # 目标函数
              eqfun=budget, eqB=w,                    # 预算约束方程和收入
              LB=c(0.001,0.001), UB=c(maxc1,maxc2))   # 搜索下界和上界
  cstar=find_cstar$pars                               # 最优化结果
  maxU0=-U_fun(cstar)                                 # 实际的最大化效用，用于后面画无差异曲线
  result=rbind(result,data.frame(case=case,c1=cstar[1],c2=cstar[2],maxU0=maxU0))
  c1vector=seq(0.1*maxc1,0.7*maxc1,length.out=10);
  c2vector=data.frame()
  for (c1 in c1vector){
    c2= uniroot(c2_u0,                                # 求无差异曲线上的c2
                c(0.001,1000),                        # 求解范围
                alpha=alpha,rho=rho,c1=c1,maxU0=maxU0,tol=0.0001)         
    c2vector=rbind(c2vector,c2$root)
  }
  data=data.frame(case=case, U0=maxU0, c1=c1vector, c2=c2vector,
                  c2_budget=(w-p1*c1vector)/p2)         # 加上预期约束方程
  colnames(data)=c("case","U0","c1","c2","c2_budget")   # 指标名称
  if (case=="Basic"){
    Basicdata=data[,3:5]
    colnames(Basicdata)=c("B_c1","B_c2","B_c2_budget")  # 基准情况
  }else{
    fig_data=rbind(fig_data,cbind(Basicdata,data))
  }
}
# 报告最优化结果
print(result)                                              
# 作图
ggplot(fig_data,aes(c1,c2,color="red"))+geom_line()+geom_line(aes(c1,c2_budget,color="red"))+
  geom_line(aes(B_c1,B_c2,color="blue"))+geom_line(aes(B_c1,B_c2_budget,color="blue"))+
  facet_wrap(~case,scales="free")+ xlab("Apple")+ylab("Fish")+
  guides(color = guide_legend(title = NULL)) + theme_bw() +
  theme(legend.position = "non")

image_1ca2qc7vpu6i1d761g0gnoi1ukj9.png-47.9kB

2. 线性代数

2.1 矩阵运算的基本命令

A=matrix(c(3,1,2,4),nrow=2)  # 建立矩阵
rowSums(A)                   # 行加总
colSums(A)                   # 列加总
a=A[,1]; t(a)%*%a            # 第1列向量的欧氏范数
I=diag(2)                    # 2维单位阵
A_T = t(A)                   # 转置
B=A+I                        # 加法
solve(B)                     # 求逆
A%*%B                        # 矩阵乘法

对应于矩阵的特征值 $\lambda_i$ 的列特征向量记为 $P_i$ ， $\Lambda$ 为特征矩阵（以特征值为主对角线），则：

$AP=[AP_1, AP_2,...AP_N] = [\lambda_1P_1, \lambda_2P_2,...\lambda_NP_N]=P\Lambda$
对应于矩阵的特征值

$\lambda_i$ 的行特征向量记为

$\tilde P_i$ ，相应地有：

$\tilde PA=[\tilde P_1A, \tilde P_2A,...\tilde P_NA] = [\lambda_1\tilde P_1, \lambda_2\tilde P_2,...\lambda_N\tilde P_N]=\Lambda\tilde P$
由于

$A^T\tilde P^T=\tilde P^T\Lambda$ ，因此

$\tilde P$ 是

$A^T$ 的列特征向量矩阵的转置矩阵。

lambda=eigen(A)$value        # 特征值
colP=eigen(A)$vectors        # 特征向量，默认为列向量  
A%*%colP                     # 检验 AP=PB
colP%*%diag(lambda)
rowP=t(eigen(t(A))$vectors)  # 特征行向量, 等于t(A)的特征列向量的转置
rowP%*%A                     # 检验 rowP*A=B*rowP
diag(lambda)%*%rowP

2.2 剑桥食谱

A=matrix(c(36,51,13,
           52,34,74,
           0,7,1.1),nrow=3,byrow=T)
b=c(33,45,3)
solve(A,b)

2.3 两部门宏观经济模型

c=0.9; beta=0.5
K=matrix(c(1-c, -c,
           beta*(1-c),   1-beta*c),nrow=2,byrow=T)
C0=100; I0=1000
v=c(C0,I0+beta*C0)
solve(K)%*%v

2.4 投入-产出表

M=matrix(c(15,20,30,
           30,10,45,
           20,60,0),nrow=3,byrow=T)  # 中间投入矩阵
d=c(35,115,70)                       # 最终需求
x=c(100,200,150)                     # 总产出
A=M/matrix(rep(x,each=3),nrow=3)     # 直接消耗系数矩阵
solve(diag(3)-A)%*%d                 # 检验最终产出公式
solve(diag(3)-A)%*%c(100,200,300)    # 给定新的最终需求，求总产出

3. 统计与计量

3.1 《定价未来》

1834年生于贝当古的法国人朱尔斯 $\cdot$ 雷格纳特(Jules Regnault)是我们故事中的一个被遗忘的英雄。...... 他的父亲是一位海关关员，在他12岁时就在穷困潦倒中去世，接着他家搬到了布鲁塞尔。作为穷人家的孩子，19岁的朱尔斯被免除了兵役，以当抄写员的收入来维持家用。与此同时，他旁听了布鲁塞尔自由大学的高级数学课程，同样被免除了学费，但他并没有拿到毕业证。

当朱尔斯28岁时，他和他的弟弟奥迪朗搬到了巴黎。他俩合租了一个很小的公寓，这个公寓面积很小并且处于顶楼，因此他们不需缴税。他们的陋室还有个优点，就是非常靠近巴黎交易所。巴黎交易所成立于1862年，两兄弟都在交易所里给经纪人助理。当他们到来时，市场已经经过了一些年的平稳增长，即将进入一个高波动的时期，这将为投资者带来风险的同时创造机遇。

当时的不稳定局面引起了金融界、法律界和经济学界的专家以及政府官员的争论，焦点集中于如何才能避免市场波动，实现可持续增长并回避灾难。......如何才能阻止投机者对金融市场功能有序发挥的破坏、促进经济持续增长呢？雷格纳特正是为了回答这个问题而完成了他的专著。

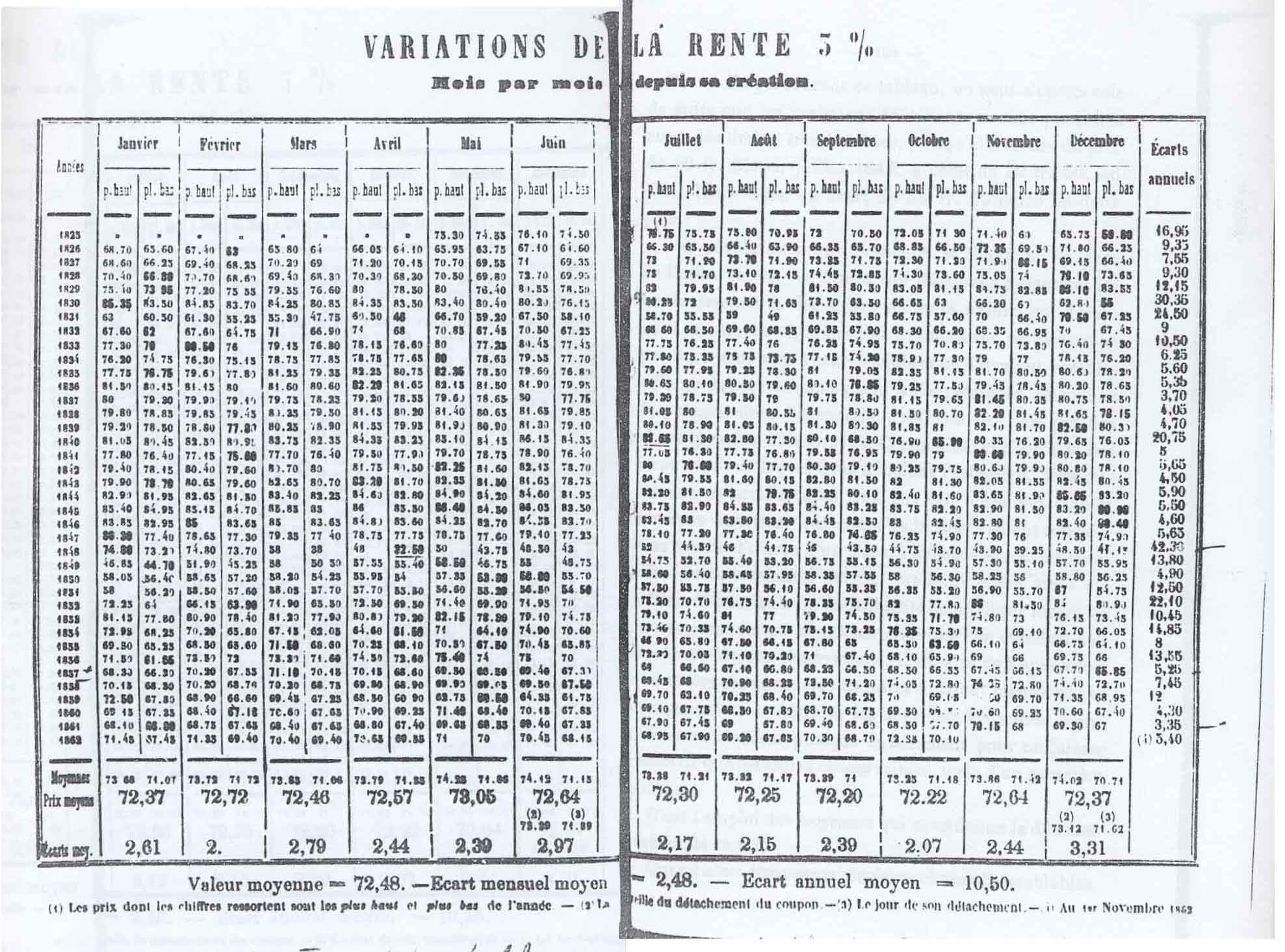
Jules Regnault(1834-1894)是第一位用数学术语来解释股票交易所运作机制的人。他用1825-1862年间法国面息3%的永续债券日频数据（超过11000个数据点）发现了：
- 证券价格的差值与所考察的时间周期的平方根成正比。（The deviation of prices is directly proportional to the squre root of time.）
- 永续债券的定价公式和交易策略。

3.2 用 lm() 做OLS回归

我们假定真实参数 $\beta=[1,~0.5,~0.1]^T$ ，并模拟出 $x$ 和 $y$ ：

$y=1+0.5x_1+0.1x_2+\epsilon$

# 生成模拟数据
N=200                                  # 样本数 
beta=c(1, 0.5, 0.1, 1)                 # 参数
K=length(beta)
x=matrix(rep(NaN,N*K),nrow=N)          # N*K 空矩阵
mu_x=c(1,0,0,0); sd_x=c(0,1,2,3)       # 均值和标准差
set.seed(1)                            # 设定随机种子使模拟结果可复制
for (k in 1:K) {                       # 模拟生成x和y
  x[,k]=rnorm(N,mu_x[k],sd_x[k])
}
y=x%*%beta
colnames(x)=c("con","x1","x2","epsilon")
mydata=data.frame(y, x)
# 估计
x=x[,1:3]
beta_bar=solve(t(x)%*%x)%*%t(x)%*%y    # 线性最小二乘估计量
myOLS=lm(y~x1+x2, data=mydata)         # OLS 回归
summary(myOLS)                         # 报告OLS回归结果

如果某个解释变量是离散变量（如年龄组），想把它设为哑变量，就用factor()。此外Kabacoff（2013）列出了 lm() 的其他常用设定，可以用来在解释变量中加入二次项、交互项，以及去掉某些解释变量：
lm.jpg-183.8kB

4. 数据与软件

4.1 数据来源

学校电子图书馆：搜数网、国泰安
公开数据：联合国、世界银行、IMF
应用数据接口(API)：Quandl、Wind
在线数据：我们的世界

4.2 软件资料

下载安装：R 和 Rstudio
补充课件：《金融数据处理与分析》（金融专业硕士课程网站）
参考教材：R.I. Kabacoff著：《R语言实战（第2版）》，王小宁、刘撷芯、黄俊文译，人民邮电出版社，2016