第六讲 计量回归基础与应用（I）

樊潇彦 复旦大学经济学院 金融数据

---

[TOC]
Ch06_Data.RData153.4kB

setwd("D:\\...\\Ch06")
rm(list=ls()) 
install.packages(c("sandwich","lmtest"))     # OLS检验
install.packages(c("gvlma","car"))           # 异方差和自相关残差调整
load("Ch06_Data.RData")

1. 计量回归模型分类

• 根据数据类型分类（括号中为适用问题的例子）：

  	$x$ 连续	$x$ 离散
  $y$ 连续	线性回归（CAPM模型等）和非线性回归	方差分析（如行业、地区、股权结构等因素对资产收益的影响）
  $y$ 离散	广义线性模型（如分红、配股、并购等决策的影响因素）

• 根据数据性质分类：

  • 截面数据（cross-section）：如上
  • 面板数据（panel）：固定/随机效应模型（Fixed/Random effect model）
  • 时序数据（time series）

2. 线性与非线性回归

2.1 古典线性回归模型：OLS估计

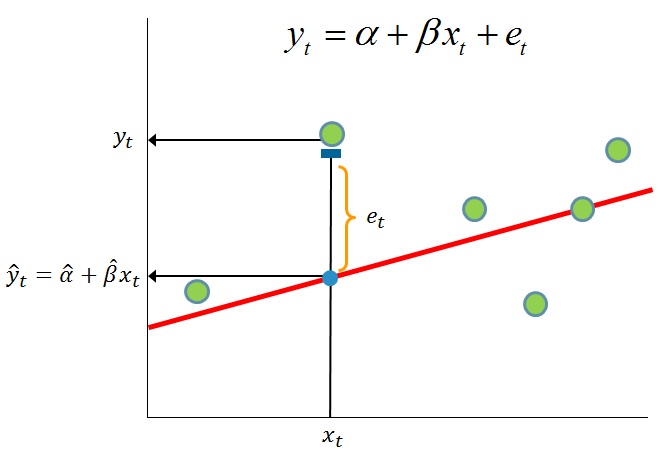
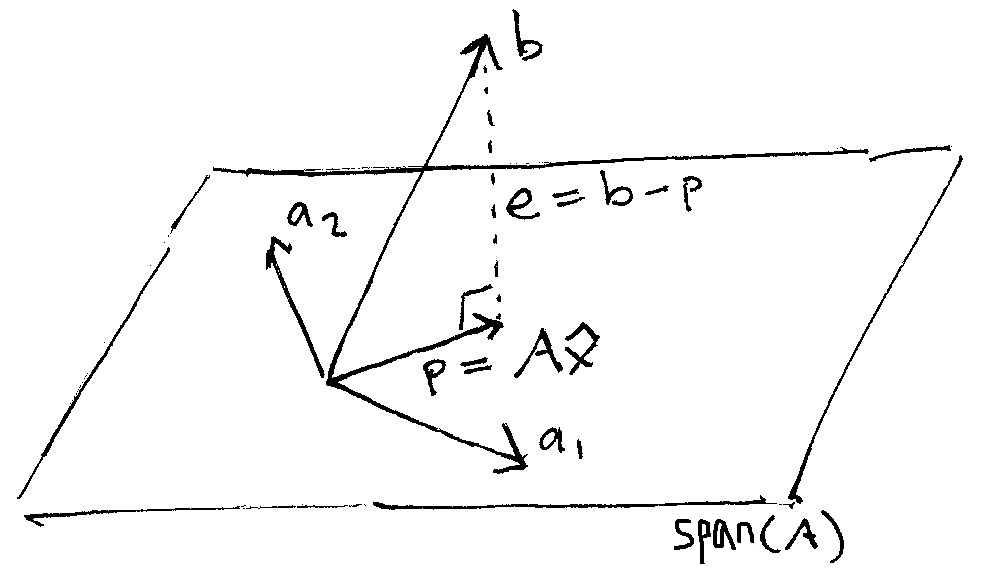
1. 模型假定
(1) 自变量 $y$ 与因变量 $X=\left(x_1,x_2...x_K\right)$ 之间存在线性关系：

$$y=X\beta + \varepsilon$$
(2) 给定数据样本，$N\times K$ 维矩阵 $X$ 满秩：
$$rank\left(X\right)=K<N,~~\text{或}~X^TX\text{可逆}$$
(3) 随机误差与 $X$ 相互独立且期望为零：
$$E\left(\varepsilon | X\right)=E\left(\varepsilon\right)=0,~~\text{或}~E\left(X^T\varepsilon\right)=0$$
(4) 随机误差之间相互独立（$E\left(\varepsilon_i\varepsilon_j\right)=0,~i\ne j$），且服从同样的正态分布（$\varepsilon_i\text{～}N\left(0,\sigma^2\right),~i=1,2...N$），用矩阵形式表示如下（其中 $\text{I}_N$ 为 $N$ 维单位方阵）：
$$\varepsilon \text{～} N\left(0,\sigma ^2 \text{I}_N\right),~~\text{或}~E\left(\varepsilon\varepsilon^T\right)=\sigma ^2 \text{I}_N$$

2. 普通最小二乘（OLS）估计

$$\begin{array}{l} {{\hat \beta }^{OLS}} = \mathop {\arg \min }\limits_\beta {\varepsilon ^T}\varepsilon = \mathop {\arg \min }\limits_\beta \left\| {y - X\beta } \right\|\\ \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{{\hat \beta }^{OLS}} = {{\left( {{X^T}X} \right)}^{ - 1}}{X^T}y}\\ {Var\left( {{{\hat \beta }^{OLS}}} \right) = {{\hat \sigma }^2}{{\left( {{X^T}X} \right)}^{ - 1}}}\\ {{{\hat \sigma }^2} = \frac{{{{\hat \varepsilon }^T}\hat \varepsilon }}{{N - K}}} \end{array}} \right. \end{array}$$

3. OLS估计量的性质

• 无偏性:
  $$E\left({\hat \beta}^{OLS}\right) = \beta,~~E\left({\hat\sigma}^2\right) = \sigma^2$$
• 有效性：
  ${\hat \beta}^{OLS}$ 是最佳线性无偏估计量（BLUE），$Var\left({\hat \beta}^{OLS}\right)$ 在所有无偏估计量的方差中最小（Gauss-Markov定理）。
• 一致性：
  $${\hat \beta}^{OLS} \mathop \to \limits^p \beta,~~{\hat\sigma}^2\mathop \to \limits^p \sigma^2，~\left(N \to \infty\right)$$
• 渐进分布：
  $${\hat \beta}^{OLS} \text{～} N\left( {\beta ,{\hat \sigma^2}{{\left( {{X^T}X} \right)}^{ - 1}}} \right)，~\left(N \to \infty\right)$$

4. 程序实现

• lm()命令和常用设定

head(olsdata)
x=as.matrix(olsdata[,2:4])
y=as.matrix(olsdata$y)
beta_bar=solve(t(x)%*%x)%*%t(x)%*%y               # 线性最小二乘估计
myOLS=lm(y~x1+x2, data=olsdata)                   # OLS 回归
summary(myOLS)                                    # 报告OLS回归结果
round(data.frame(betaOLS=myOLS$coefficients, beta=beta_bar),3)  # 结果比较

如果某个解释变量是离散变量（如年龄组），想把它设为哑变量，就用factor()。此外Kabacoff（2013）列出了 lm() 的其他常用设定，可以用来在解释变量中加入二次项、交互项，以及去掉某些解释变量：

5. 回归诊断
所谓回归诊断，就是判断回归模型是否符合古典线性回归的各项假定。用 gvlma 包中的 gvlma() 函数可以对模型假定进行综合检验，另外car包则提供了对多重共线性vif()、残差自相关durbinWatsonTest()和异方差ncvTest()等问题的检验命令。

library(gvlma)
gvlma(myOLS)                # 模型假定是否可接受
library(car)
vif(myOLS)>4                # 检验多重共线性问题
durbinWatsonTest(myOLS)     # 检验残差自相关问题
ncvTest(myOLS)              # 检验异方差问题

当古典线性回归模型的假定不成立时，需要改进估计方法。当假定(3)不成立，解释变量存在内生性问题时，可以通过寻找工具变量的方法解决。由于这种情况在金融数据分析中并不多见，因此不再赘述，下面我们依次介绍违反同方差假定(4)、解释变量线性无性假定(2)，以及线性方程关系假定(1)时的处理方法。

2.2 存在异方差和残差自相关时的拓展：GLS估计

古典线性回归模型的假定(4)不成立，存在异方差和残差自相关问题，将影响参数估计的有效性，使置信区间估计和统计检验有误：

$$\varepsilon \text{～} N\left(0,\sigma^2\Omega\right),~~~\Omega \ne \rm{I_N}$$
广义最小二乘（Generalized least squares, GLS）估计：
$$\begin{array}{*{20}{l}} {{{\hat \beta }^{GLS}} = {{\left( {{X^T}{\Omega ^{ - 1}}X} \right)}^{ - 1}}{X^T}{\Omega ^{ - 1}}y}\\ {Var\left( {{{\hat \beta }^{GLS}}} \right) = {{\hat \sigma }^2}{{\left( {{X^T}{\Omega ^{ - 1}}X} \right)}^{ - 1}}}\\ {{{\hat \sigma }^2} = \frac{{{{\hat \varepsilon }^T}\hat \varepsilon }}{{N - K}}} \end{array}$$
由于我们不可能根据 $N$ 个样本估计出对称矩阵 $\Omega$ 中的 $N(N+1)/2$ 个元素，因此在实际应用中，一般先做OLS估计，再根据方差检验结果对 $\Omega$ 的具体形式做简化假定（如只考虑异方差、自相关，或直接假定 $\omega_{ij}$ 的函数形式），最后用简化的 $\hat\Omega$ 作为 $\Omega$ 的一致估计，得到FGLS（Feasible GLS）估计量。
以前面对olsdata的myOLS估计为例，检验结果表明在8%的显著性水平上存在异方差问题，这种情况下对 $\beta$ 的估计无偏，但不再有效，因此要对估计出的参数标准差做相应调整：

library(sandwich)
sd=sqrt(diag(vcov(myOLS)))
sd_adjust=sqrt(diag(vcovHC(myOLS)))        # 如果不仅有异方差，还有残差的自相关，用 vcovHAC() 代替
round(data.frame(sd, sd_adjust),3)         # 比较 beta 的标准差
library(lmtest)
coeftest(myOLS,vcov=vcovHC)                # 报告调整标准差后的结果

2.3 多重共线性与模型选择

如果解释变量很多，就很容易出现变量之间存在共线性，或者有的回归系数不显著的情况，此时我们需要对解释变量做出取舍，以决定最终的回归方程，这就是模型选择问题。具体可以通过anova()和AIC()命令来实现：

ols1=lm(y~x1+x2, data=olsdata)             # 两个待比较的模型
ols2=lm(y~x1, data=olsdata)       
anova(ols1,ols2)                           # 两个模型是否显著不同
AIC(ols1,ols2)                             # 两个模型的AIC值，选择AIC较小的模型

2.4 非线性回归模型：NLS估计

放弃古典线性回归模型的假定(1)，允许自变量和因变量之间存在非线性关系：

$$y = f\left(X;\theta \right) + \varepsilon$$
如经济学问题中的CES生产函数估计等。相应的非线性最小二乘（NLS）估计为：
$${\hat \theta}^{NLS} = \mathop {\arg \min }\limits_\theta \varepsilon^T\varepsilon = \mathop {\arg \min }\limits_\theta \left\| {y - f\left( {X;\theta } \right)} \right\|$$
假定待估方程为：
$$y=a+\left(0.49-a\right)e^{-b(x-8)}+\epsilon$$

nls.sol<-nls(Y~a+(0.49-a)*exp(-b*(X-8)),            # 设定方程
             start = list( a= 0.1, b = 0.01 ),      # 参数初始值
             data=nlsdata)                          # 数据
summary(nls.sol)                                    # 报告NLS回归结果

3. 应用：检验CAPM模型

# 1. 加载数据
class(casestudy1.data0.00)
head(casestudy1.data0.00)
time=index(casestudy1.data0.00, format ='%Y-%m-%d')
data=data.frame(time,coredata(casestudy1.data0.00))
names(data)
# 2. 选取部分数据作图
# GE          | GE stock
# SP500       | S&P500 Index
# DGS3MO      | 3-Month Treasury, constant maturity rate
# DGS1        | 1-Year Treasury, constant maturity rate
# DGS5        | 5-Year Treasury, constant maturity rate
# DGS10       | 10-Year Treasury, constant maturity rate#
# DAAA        | Moody's Seasoned Aaa Corporate Bond Yield 
# DBAA        | Moody's Seasoned Baa Corporate Bond Yield #
# DCOILWTICO  | Crude Oil Prices: West Text Intermediate (WTI) - Cushing, Oklahoma
## GE、SP500和油价
stockdata=data[,c("GE","SP500","DCOILWTICO")]
mapstock=scale(stockdata,center=T)                # Scaling and Centering of Matrix-like Objects
mapstock=data.frame(time, mapstock)%>%
  gather(stock, p, -time)
Lehman=min(which(mapstock$time ==as.Date("2008/9/15",tz="CST")))
ggplot(mapstock,aes(x=time, y=p, color=stock)) +
  geom_line() +  
  geom_vline(aes(xintercept = as.numeric(time[Lehman]))) +
  theme_bw()
## 3个月、1年、5年、10年期国债，及AAA和BAA企业债
bonddata=data[,c(1,7:12)]
mapbond=gather(bonddata, bond, r, -time)
ggplot(mapbond,aes(x=time, y=r, color=bond)) +
  geom_line() +  
  geom_vline(aes(xintercept = as.numeric(time[Lehman]))) +
  theme_bw()

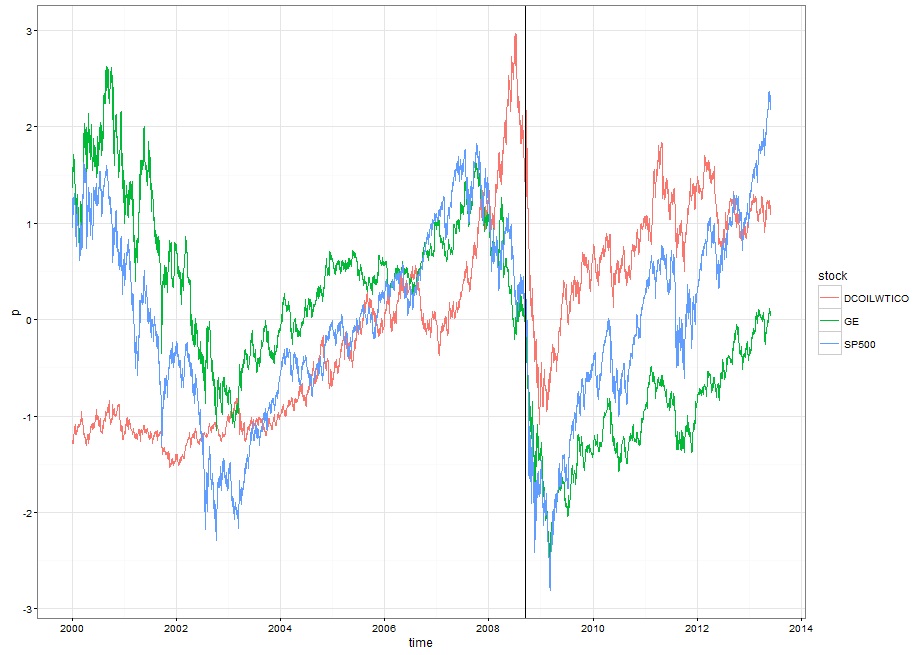
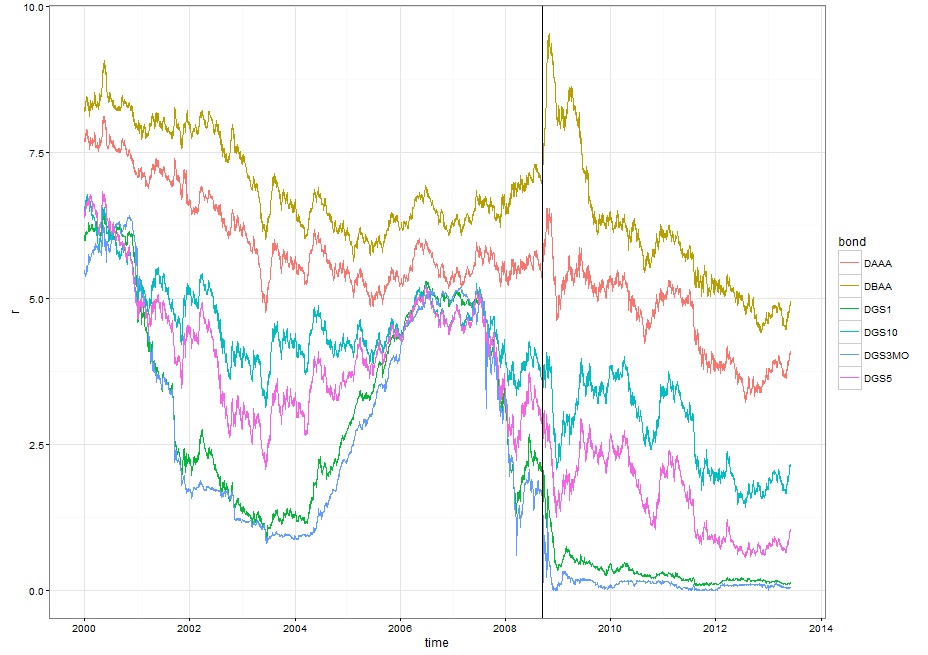
# 3. 计算指标
# （1）日收益率
r=diff(log(casestudy1.data0.00[,c("GE","SP500","DCOILWTICO")]))
time=index(r)
r=data.frame(time,coredata(r))
# 注意：计算无风险债券的日收益率，需要将年化收益率转化为按360个交易日计算的日收益率
rf<-log(1 + .01*coredata(casestudy1.data0.00[-1,"DGS3MO"]) *
                        diff(as.numeric(time(casestudy1.data0.00)))/360)
dimnames(rf)[[2]]="rf"
# (2) 计算超额收益并作图
erGE=r$GE-rf
dimnames(erGE)[[2]]="erGE"
erSP500=r$SP500 - rf
dimnames(erSP500)[[2]]="erSP500"
erOIL=r$DCOILWTICO - rf
dimnames(erOIL)[[2]]="erOIL"
capmdata<-data.frame(time, erGE, erSP500, erOIL)
dim(capmdata)
ggplot(capmdata,aes(x=erSP500,y=erGE,color=time)) +
  geom_smooth(method="lm") +
  geom_point() + geom_vline(xintercept = 0) + geom_hline(yintercept = 0) +
  theme_bw()

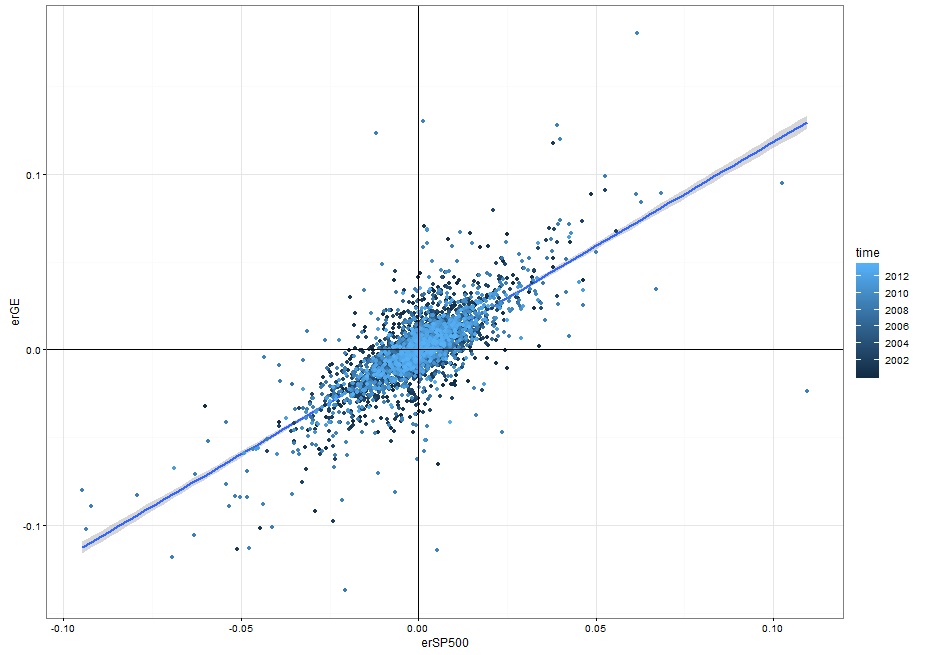
# (3) OLS回归检验CAPM模型
lmfit0<-lm(erGE ~ erSP500, data=capmdata)           # 回归结果存为 lmfit0 对象
names(lmfit0)                                       # 查看对象中的内容
summary(lmfit0)
lmfit1<-lm( erGE ~ erSP500 + erOIL, data=capmdata)  # 用油价做为宏观因子
summary.lm(lmfit1)

课后练习

1. 将企业债也视为一种风险资产，用1年期国债作为债券市场指数，计算两种企业债（AAA和BAA）的 $\beta$ 系数，并检验CAPM模型。

2. 先用下面的命令将日数据转换为月度数据，再用GE数据检验CAPM模型

library(xts)
data.monthly <- casestudy1.data0.00[endpoints(casestudy1.data0.00, on="months", k=1), ]
time.monthly=format(index(data.monthly),'%Y%m')
data.monthly=data.frame(time=time.monthly,coredata(data.monthly))
head(data.monthly)

参考资料

1. MIT Open Course Topics in Mathematics with Applications in Finance (18.S096), Case studies 1
2. Kleiber, C. and A. Zeileis 2008: Applied Econometrics with R (Use R!), Springer
3. R.I. Kabacoff著：《R语言实战（第2版）》，王小宁、刘撷芯、黄俊文译，人民邮电出版社，2016
4. 薛毅、陈立萍编著，2012：《统计建模与R软件》，清华大学出版社