第八讲 平稳时间序列线性模型

樊潇彦 复旦大学经济学院 金融数据

---

0. 准备工作

下载数据：Ch08.rar

setwd("D:\\...\\Ch08")
rm(list=ls())
install.packages("forecast","timeDate","timeSeries","fBasics","tseries")
## 调用
library(tidyverse)
library(readxl)
library(ggplot2)
library(forecast)
library(timeDate)
library(timeSeries)
library(fBasics)
library(tseries)

1. 随机过程和时间序列基本概念

1.1 定义和数字特征

随机过程（stochastic process）是随机变量按时间编排的集合。设对每个参数 $t\in T$，$Y\left(t,\omega\right)$ 都是一个随机变量，则称下面的随机变量族为随机过程：

$$Y_T=\left\{Y\left(t,\omega\right)|Y:T\times\Omega\to\mathbb{R}\right\}$$

根据时间参数 $t$ 是否连续，可分为：

• 随机过程（process）：$t \in \left(-\infty,\infty\right)$ 为不可列的连续变量。
• 时间序列（series）：$t \in \left\{...-2,-1,0,1,2...\right\}$ 为可列的离散变量。
  平稳时间序列的常用数字特征有：

数字特征	公式
均值	$\mu=E\left( {{Y_t}} \right)$
方差	$\gamma_0 = Var\left( {{Y_t}} \right)=E\left[ {{{\left( {{Y_t} - \mu} \right)}^2}} \right]$
协方差	$\gamma_k =Cov({Y_t,Y_{t-k}})=E\left[ {\left( {{Y_t} - \mu} \right)\left( {{Y_{t-k}} - \mu} \right)} \right]$
自相关系数（ACF）	${\rho _k} = \gamma_k/\gamma_0$
偏自相关系数（PACF）	$\phi_{kk}$：在 AR(k-1) 模型基础上添加 $x_{t-k}$ 对解释 $x_t$ 的贡献

# Tsay(2015)：P33，例2.1
d10=read.table("m-dec12910.txt",header=T)$dec10
dec10=ts(d10,frequency=12,start=c(1967,1))  # 转换为ts对象
par(mfcol=c(3,1))                           # 设定绘图窗口3*1
plot(dec10,xlab='year',ylab='returns')     
title(main='(a): Simple returns')
f1=acf(d10,lag=24,plot=T)                   # 计算acf并作图
pacf(d10, lag=24, plot=T)                   # 计算pacf并作图
f1$acf[13]                                  # 显示gamma_13 > 0
f1$acf[13]*sqrt(length(d10))                # 检验1月效应(P33-34,例2.1)，H0:gamma_13=0
Box.test(d10,lag=24,type='Ljung')           # Ljung-Box Q检验，H0: gamma_1=gamma_2=...=gamma_24=0
# CAPM理论假定收益率不可预测、无自相关性，因此Ljung-Box Q检验可以用来检验有效市场假说。

1.2 随机过程分类

• 严格平稳（strict stationary）： $\forall t_1,t_2...t_N\in T$ 和 $s>0$，如果 $Y_{t_1+s},Y_{t_2+s}...Y_{t_N+s}$ 和 $Y_{t_1},Y_{t_2}...Y_{t_N}$ 有相同的联合分布，则 $Y_T$ 严平稳。
  我们把具有有限均值、有限方差的独立同分布随机变量序列称为白噪声序列（white noise），常用的有 $\varepsilon_t \text{~} N(0,\sigma^2)$。显然，白噪声序列严格平稳。
• 弱平稳（week stationary）：$\forall t\in T$，均值 $E\left(X\right)=\mu$ 和协方差 $Cov\left(Y_t,Y_{t-k}\right)=\gamma_k$ 不随时间 $t$ 而变化，则 $Y_T$ 弱平稳（或宽平稳、协方差平稳）；
• 非平稳（non-stationary）：不满足上述两种定义的随机过程，是非平稳的。
  很多时间序列数据都有时间趋势（trend）和季节性变化（seasonality）的特征，根据 Fan and Yao(2015)，包含时间趋势和季节性因素的时序数据经处理后可能变为平稳的时间序列，单位根等非平稳时序也可以通过差分的方法转换为平稳时序。

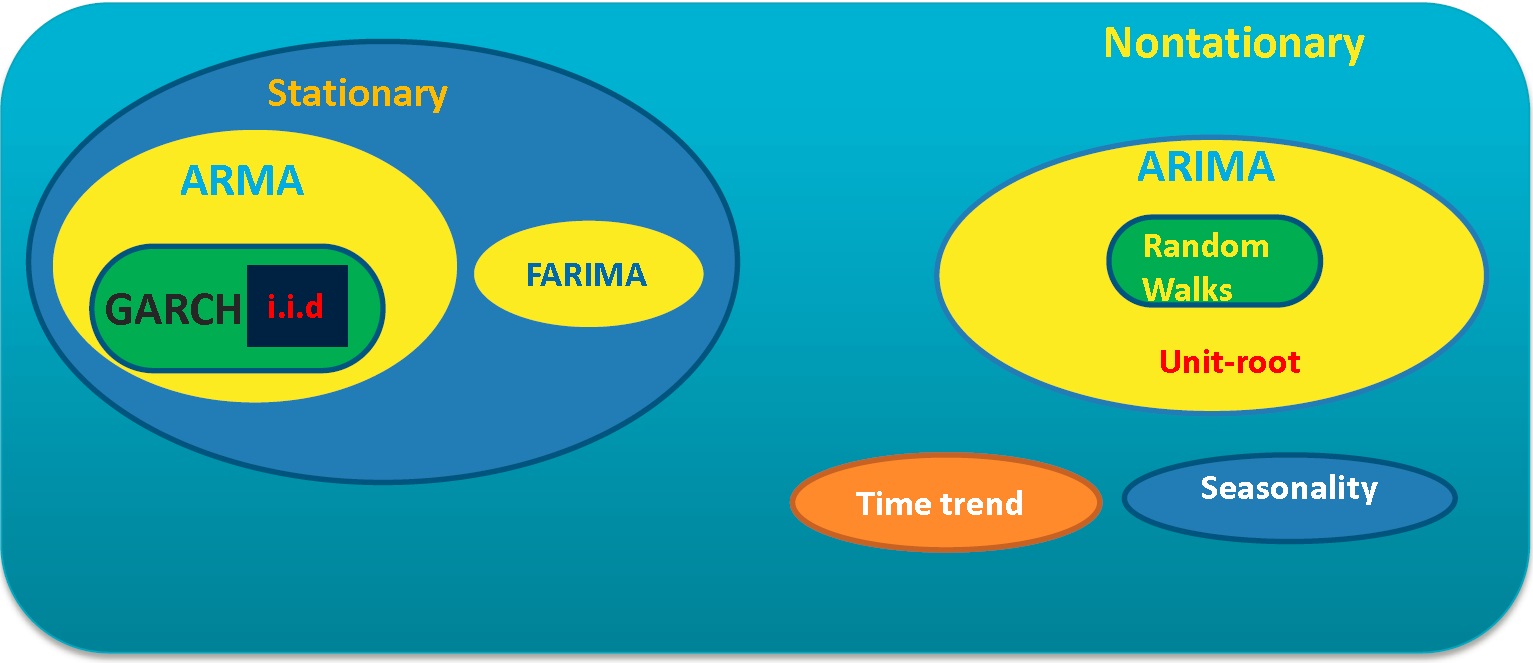
1.3 常用平稳和非平稳时序数据模型与转换关系

• 平稳（stationary）：
  
  • $AR\left(p\right)$：$p$ 阶自回归（autoregressive）
    $$y_t=\phi_0 +\phi_1y_{t-1}+...+\phi_py_{t-p}+\varepsilon_t$$
  • $MA\left(q\right)$：$q$ 阶移动平均（moving average）
    $$y_t=\mu+\varepsilon_t-\theta_1\varepsilon_{t-1}...-\theta_q\varepsilon_{t-q}$$
  • $ARMA\left(p,q\right)$：$\left(p,q\right)$ 阶自回归移动平均（autoregressive moving average）
    $${y_t} = \phi_0 + {\phi _1}{y_{t - 1}} + ... + {\phi _p}{y_{t - p}}\\ ~~+ {\varepsilon _t} - {\theta _1}{\varepsilon _{t - 1}}... - {\theta _q}\varepsilon _{t - q}$$
• 非平稳（non-stationary）：
  
  • 不带漂移的随机游走（random walk）或单位根（unit-root）过程：
    $$y_t=y_{t-1}+\varepsilon_t$$
  • 带漂移的随机游走（random walk with drift）：
    $$y_t=\delta+y_{t-1}+\varepsilon_t$$
  • 带趋势的随机游走（random walk with trend）
    $$y_t=\beta t+y_{t-1}+\varepsilon_t$$

通过积分和差分，可以实现平稳与非平稳数据之间的转换：

• 平稳序列经过 $d$ 阶积分后可以变为非平稳序列。
  例如：白噪声过程的一阶积分为 ${y_t} = \sum\limits_{s = 0}^t {{\varepsilon _0}}$，其方差 $Var\left( {{y_t}} \right) = t{\sigma ^2}$ 将随着 $t$ 的增加而增加，不存在稳态分布。由平稳序列经过 $d$ 阶积分得到的非平稳序列称为 $d$ 阶单积（integrated of order d）序列，记为 $y_t\text{～}I\left(d\right)$。
• 非平稳序列 $y_t$ 经过 $d$ 阶差分后可变为平稳序列。
  例如：单位根过程经一阶差分后变为白噪声过程：$\Delta {y_t} = {y_t} - {y_{t - 1}} = {\varepsilon _t}$。一般地，如果 $y_t$ 经过 $d$ 阶差分后变为 $ARMA\left(p,q\right)$ 过程，则称为 $ARIMA\left(p,d,q\right)$ 过程。

1.4 平稳和非平稳数据检验

一、数据示例：

1 上证综指与收益率

library(quantmod) 
# 下载上证综指无法下载可直接 load("ssec.RData")    
ssec<-getSymbols("000001.SS",from = "1991-07-15",to = Sys.time(),
                 src = "yahoo",auto.assign=FALSE)            
ssec.m<-to.monthly(ssec)                                     # 转换成月度数据
chartSeries(ssec.m,type="candlesticks",theme="white", name = "上证综指月线图",
            time.scale = "",up.col="red",dn.col="green")

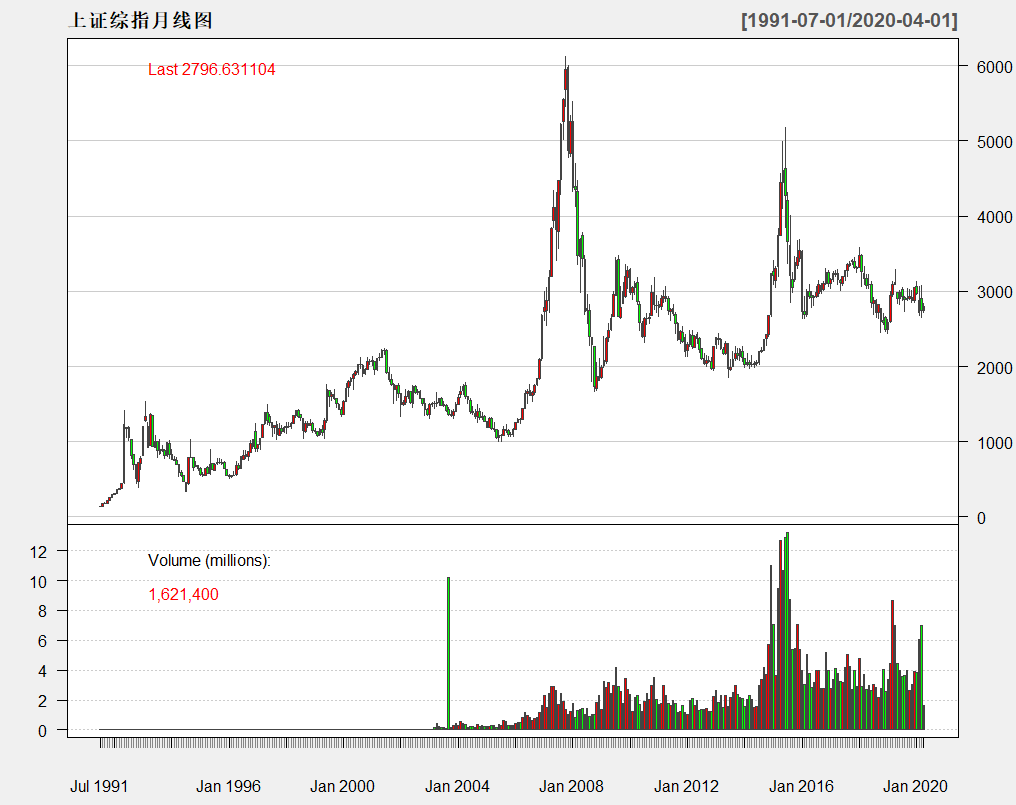
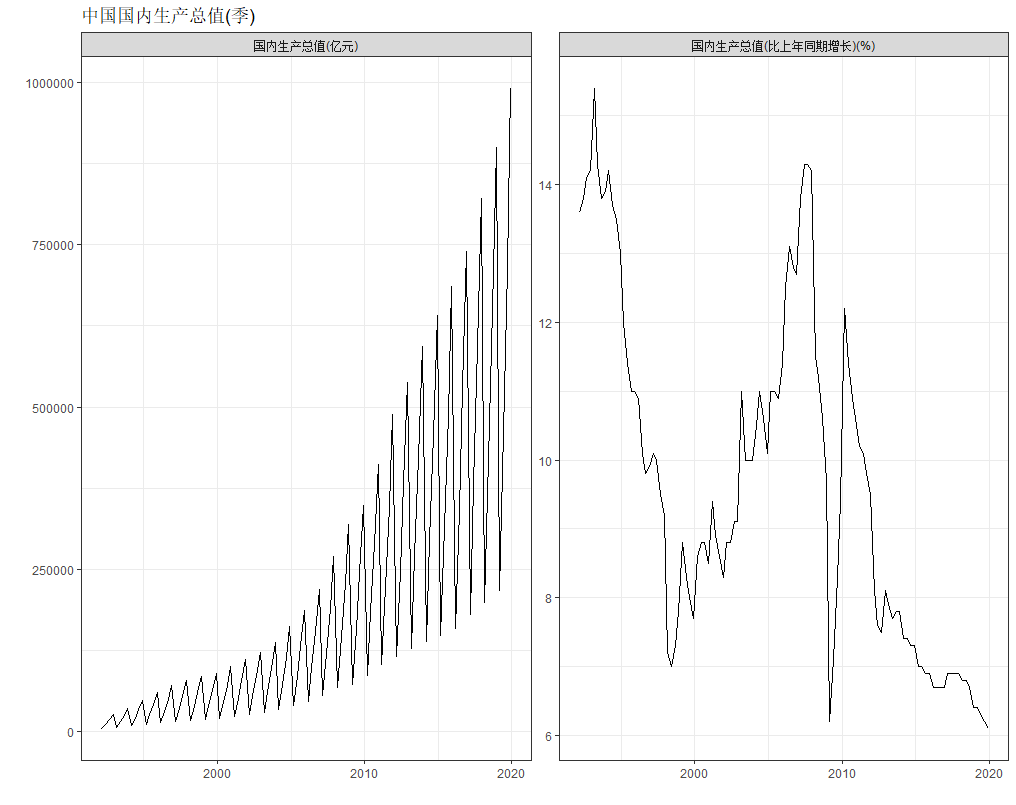
2 季度GDP与名义增长率
学校电子图书馆有很多中文数据库，下面以国泰安中季度国内生产总值为例，说明宏观经济数据的特征。

library(readxl)
Qgdp=read_excel("CME_Qqgdp.xlsx", skip=3, col_names =F)
colnames(Qgdp)=colnames(read_excel("CME_Qqgdp.xlsx"))        # 更改指标名
str(Qgdp)                                                    # 查看数据结构
library(zoo)
Qgdp=Qgdp%>%mutate(time=as.yearmon(Quarter))%>%
  rename('国内生产总值(亿元)'=Gdp,
         '国内生产总值（比上年同期增长）(%)'=Gdpcurrperiod)%>%
  select(time,'国内生产总值(亿元)','国内生产总值（比上年同期增长）(%)')
ggplot(Qgdp%>%gather(var,value,-time),aes(time,value))+
  geom_line()+facet_wrap(~var,scales="free")+
  labs(title="中国国内生产总值（季）",x="",y="")+theme_bw()

二、平稳性检验：

ssec.m97=ssec.m[index(ssec.m)>as.yearmon("1997-01"),]  # 1996年12月16日开始有10%涨跌幅度限制
ln_ssec=log(ssec.m97$ssec.Adjusted)                    
plot(ln_ssec, main="上证综指对数值")
# 计算月收益率，由于月收益率可能较大，不用diff(log(x))
ssec.m97$ret=diff(ssec.m97$ssec.Adjusted) / lag(ssec.m97$ssec.Adjusted) * 100   
ret=ssec.m97$ret[-1,]                                  # 去掉第一行缺失值
plot(ret, main="上证综指月收益率（%）")
library(tseries)
pp.test(ln_ssec)                                       # DF检验，H0：非平稳
pp.test(ret)                                       
adf.test(ln_ssec)                                      # ADF检验，H0：非平稳
adf.test(ret)                                      
kpss.test(ln_ssec)                                     # KPSS检验，H0：平稳
kpss.test(ret)  

2. 常用平稳时序线性模型

2.1 简单自回归模型 AR(p)

1. 定义和常用统计量：
   $${y_t} = {\phi _0} + {\phi _1}{y_{t - 1}} + ... + {\phi _p}{y_{t - p}} + {\varepsilon _t}$$
   记 $\phi \left( L \right) = 1 - \sum\limits_{i = 1}^p {{\phi _i}{L^i}}$ 为滞后算子的多项式，上式也可以写为：
   $$\phi \left( L \right){y_t} = {\phi _0} + {\varepsilon _t}$$

常用统计量	以 AR(1) 过程为例
均值	$\mu=\frac{\phi_0}{1-\phi_1}$
方差	$\gamma_0=\frac{\sigma^2}{1-\phi^2_1}$
自相关系数（ACF）	$\rho_k=\phi^k_1$
偏自相关系数（PACF）	$\phi_{kk}= \phi_1 (k=1), ~\phi_k=0 (k>1)$

2. 平稳性条件：

• AR(1)过程等价于一元一阶差分方程：
  $$\begin{array}{l} {y_t} = \phi_0 + \phi_1 {y_{t - 1}} + {\varepsilon _t}\\ ~~~= \phi_0 + \phi_1 (\phi_0 + \phi_1 {y_{t - 2}} + {\varepsilon _{t - 1}}) + {\varepsilon _t} = ...\\ ~~~= \phi_0 \sum\limits_{s = 0}^t {{\phi ^s_1}} + \sum\limits_{s = 0}^t {{\phi ^s_1}{\varepsilon _{t - s}}} \end{array}$$
  由于 $\frac{\partial {y_t}}{\partial {\varepsilon _0}} = {\phi ^t_1}$，当时间 $t\to \infty$ 时，$y_t$ 的平稳性意味着当期的随机冲击影响有限，这等价于 $|\phi_1|<1$。 否则 $\phi_1>1$ 时 $y_t$ 会单调发散，$\phi_1<-1$ 时会震荡发散。
• AR(p) 过程等价于一元高阶差分方程： $$y_t=\phi_0+\phi_1y_{t-1}+\phi_2y_{t-2}...+\phi_py_{t-p}+\varepsilon_t$$ 可以用降阶增元的方法改写为 多元一阶差分方程组 $Y_t= \mathbf{\mu} + \Phi {Y_{t - 1}} + \mathbf{\varepsilon_t}$：
  $$\left[ {\begin{array}{*{20}{c}} {{y_t}}\\ {{y_{t - 1}}}\\ \vdots \\ {{y_{t - p+1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \phi_0 \\ 0\\ \vdots \\ 0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\phi _1}}&{{\phi _2}}& \cdots &{{\phi _p}}\\ 1&0& \cdots &0\\ \vdots & \ddots & \ddots & \vdots \\ 0& \cdots &1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{y_{t - 1}}}\\ {{y_{t - 2}}}\\ \vdots \\ {{y_{t - p}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\varepsilon _t}}\\ 0\\ \vdots \\ 0 \end{array}} \right]$$
  上述方程组也可以写为 $\left( {I - \Phi L} \right){Y_t} = \mathbf{\mu + \varepsilon_t}$，根据汉密尔顿(1999)，$\Phi$ 的特征根是下述特征方程的解 $z$ 的倒数：
  $$1-\phi_1z-\phi_2z^2-...\phi_pz^p=0$$
  当 $\left||z_i\right||>1,~(i=1,2...p)$ 时，$\Phi$ 的所有特征根的模都小于1 （$\left||\lambda_i\right|| < 1$）时，有平稳解：
  $${Y_t} = {\left( {I - \Phi L} \right)^{ - 1}}\left(\mathbf{\mu + \varepsilon_t}\right)$$
  其中 ${\left( {I - \Phi L} \right)^{ - 1}} = I + \Phi L + {\left( {\Phi L} \right)^2} + ... = \sum\limits_{j = 0}^{ + \infty } {{{\left( {\Phi L} \right)}^j}}$。

2.2 移动平均模型 MA(q)

1. 定义和常用统计量：
   $$\begin{array}{l} {y_t} = \mu + {\varepsilon _t} - {\theta _1}{\varepsilon _{t - 1}}... - {\theta _q}{\varepsilon _{t - q}}\\ ~~~ = \mu + \theta \left( L \right){\varepsilon _t} \end{array}$$
   其中：$\theta \left( L \right) = 1 - \sum\limits_{i = 1}^q {{\theta _i}{L^i}}$

常用统计量	以 MA(1) 过程为例
均值	$\mu$
方差	$\gamma_0=(1+\theta^2_1)\sigma^2$
自相关系数（ACF）	$\rho_k=\frac{-\theta_1}{1+\theta^2_1}(k=1), ~\rho_k=0 (k>1)$
偏自相关系数（PACF）	$\phi_{kk}= \theta^k_1$

2. 平稳性条件：
移动平均过程总是平稳的。当 $|\theta_1|<1$ 时，$MA(1)$ 过程可逆，即可以转换为 $AR(\infty)$ 过程：

$$\begin{array}{l} {y_t} = \mu + {\varepsilon _t} - {\theta _1}{\varepsilon _{t - 1}}\\ \;\;\;\; = \mu + {\varepsilon _t} - {\theta _1}\left( {{y_{t - 1}} - \mu {\rm{ + }}{\theta _1}{\varepsilon _{t - 2}}} \right)\\ \;\;\;\; = - {\theta _1}{y_{t - 1}} + \left( {1 + {\theta _1}} \right)\mu + {\varepsilon _t} - \theta _1^2\left( {{y_{t - 2}} - \mu + {\theta _1}{\varepsilon _{t - 3}}} \right)\\ \;\;\;\; = ... = \frac{\mu}{{1 - {\theta _1}}} + \sum\limits_{s = 1}^\infty {\theta _1^s{y_{t - s}}} + {\varepsilon _t} \end{array}$$

2.3 自回归移动平均模型 ARMA(p,q)

1. 定义和常用统计量：
   $${y_t} = \phi_0 + {\phi _1}{y_{t - 1}} + ... + {\phi _p}{y_{t - p}}\\ ~~~~~+ {\varepsilon _t} - {\theta _1}{\varepsilon _{t - 1}}... - {\theta _q}{\varepsilon _{t - q}}$$
   也可以表示为：
   $$\phi \left( L \right){y_t} = {\phi _0} + \theta \left( L \right){\varepsilon _t}$$

常用统计量	以 ARMA(1,1) 过程为例
均值	$\mu=\frac{\phi_0}{1-\phi_1}$
方差	$\gamma_0=\frac{(1-2\phi_1\theta_1+\theta^2_1)\sigma^2}{1-\phi^2_1}$
自相关系数（ACF）	$\rho_k=\phi_1-\frac{\theta_1\sigma^2}{\gamma_0}(k=1), ~\rho_k=\phi_1\rho_{k-1} (k>1)$
偏自相关系数（PACF）	$\phi_{kk}= \phi_k + \theta^k_1$

2. 平稳性条件：
与 AR(p) 模型类似，ARMA(p,q) 模型的平稳性要求矩阵 $\Phi$ 的所有特征根的模均小于1。

3. 应用：模型回归与预测

模型回归的第一步是在 AR、MA 和 ARMA模型中做出选择，做 ACF 和 PACF 图将很有帮助。

-	AR(p)	MA(q)	ARMA(p,q)
ACF	衰减	$q$ 阶截尾	衰减
PACF	$p$ 阶截尾	衰减	衰减

实际应用中，forcast 包中的 auto.arima() 命令，可以自动识别 ARIMA(p,d,q) 中各个阶数，非常方便。

3.1 上证综指月度收益率

library(fBasics) 
basicStats(ret)                                       # 对月度收益率的基本统计描述
t.test(ret)                                           # 均值检验 H0: x=0 
normalTest(ret,method='jb',na.rm=T)                   # 正态分布检验，JB-test
par(mfcol=c(1,1))  
acf(ret, lag=12, plot=T)                              # 自相关系数作图
Box.test(ret,lag=6,type='Ljung')                      # m阶自相关系数为零的检验
library(forecast)
regssecm=auto.arima(ret,stationary = TRUE, seasonal = FALSE, 
              ic="aic")  
regssecm                                              # 回归结果：ARIMA(2,0,1)
# 拟合与预测
par(mfcol=c(2,1))                                     # 设作图窗口2行1例
plot(regssecm$x, lty = 1, main = "上证综指收益率(%)")
lines(fitted(regssecm), lty = 2,lwd = 2, col = "red")
predict(regssecm, n.ahead=3)
plot(forecast(regssecm))

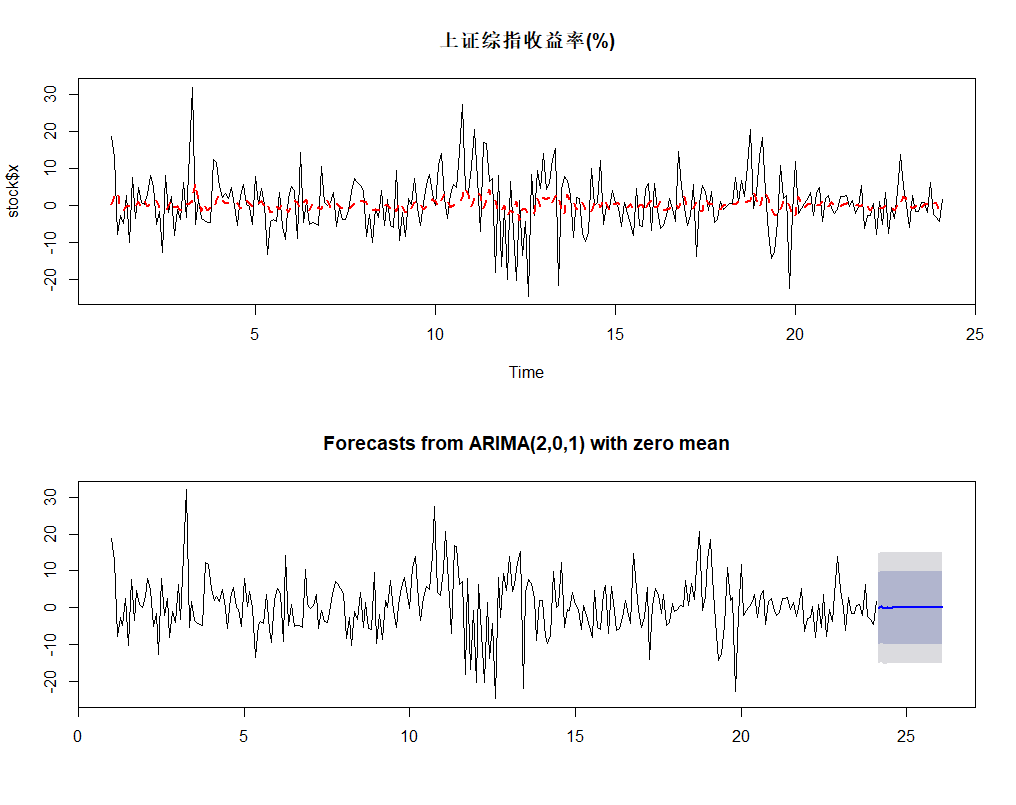
3.2 美国GNP

# Tsay(2015)：P41，例2.3
G=read.table("q-gnp4710.txt",header=T)$VALUE              # 读取GNP数据
gnp=diff(log(G))                                          # 增长率
pp.test(gnp)                                              # DF检验，H0:有单位根
adf.test(gnp)                                             # ADF检验，H0:有单位根
tdx=c(1:253)/4+1947                                       # 时间指标
par(mfcol=c(2,1))                                         # 设定作图窗口
plot(tdx,G,xlab='year',ylab='GNP',type='l')               # GNP
plot(tdx[2:253],gnp,type='l',xlab='year',ylab='growth')   # 增长率
acf(gnp,lag=12)                                           # ACF
pacf(gnp,lag=12)                                          # PACF
m1=arima(gnp,order=c(3,0,0))                              # 回归AR(3)
m1
library(forecast)
m2=auto.arima(gnp,stationary = TRUE, seasonal = FALSE, 
              ic="aic")                                   # 自动回归命令，结果一样
m2
# 模型检验，作图检验残差应满足三个标准：（1）不存在波动集聚；（2）ACF图没有自相关；（3）Ljung-Box检验所有自相关系数均为零
tsdiag(m1, gof=12)    
# 拟合与预测
par(mfcol=c(2,1))
plot(m2$x,lty = 1, main = "美国GNP增长率", 
     ylab = "Return in percent", xlab = "Date")
lines(fitted(m2), lty = 2,lwd = 2, col = "red")
predict(m2, n.ahead=3)
plot(forecast(m2))
# 周期分析
phi=c(1,-m1$coef[1:3]); z=polyroot(phi)     # 设定和求解多项式
z                                           # 两个共轭复数、一个小于零的实数
Mod(z)                                      # 检验：z的模>1，对应特征根的模<1
2*pi/acos(Re(z)/Mod(z))[1]                  # 计算经济周期平均持续时间

作业

1. 下载美国实际GDP增长率数据，检验平稳性、用ARIMA模型预测美国未来一年的实际经济增长率。
2. 分析中国季度GDP名义增长率数据，检验平稳性、做ARIMA模型分析并预测未来一年的名义经济增长率。

参考文献

1. Daroczi, C. et al. 2013: Introduction to R for Quantitative Finance, Packt Publishing Ltd.
2. Tsay, R.S. 2013：《金融时间序列分析（第3版）》，王远林、王辉、潘家柱译，人民邮电出版社