约瑟夫问题与成套方法

数学

---

这篇学习笔记探讨约瑟夫问题以及由该问题衍生的求解递归式的成套方法，来源于《具体数学》第一章。

问题介绍

约瑟夫问题的来源是这样的：在犹太罗马战争期间，41名犹太反抗者困在了罗马人包围的洞穴中。这些反抗者宁愿自杀也不愿被活捉，于是决定围成一个圈，并沿着圆圈每隔两人杀死一人，直到剩下最后两人为止。但是约瑟夫和一个未被告发的同谋者不希望无谓地自杀，于是他迅速计算出他和其朋友在这个圆圈中应该站的位置。

现在我们把问题抽象一下：从围成标有几号 1 到 n 的圆圈的 n 个数开始，每隔一个数就删去一个数，直到剩下最后一个数，要求解剩余数的一般表达式 J(n)。

这是 n 为 10 的情况，删除的顺序是 2 4 6 8 10 3 7 1 9，留下的数为 5。

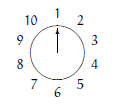
现在，我们来考虑一般情况，假设一开始有 2n 个数，经过第一轮删除后只剩下奇数：

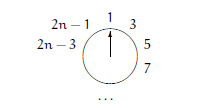
而 3 是下一个要被删除的数。除每个数加倍然后减 1 以外，这正像是对应 n 个人开始时的情况。也就是说：

$$J(2n) = 2J(n) - 1, n ≥ 1.$$
对于一开始有 2n+1 个数，经过第一轮删除，情况是这样的：

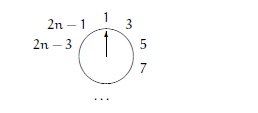
不难看出，这一次可以推出下面的递推式：

$$J(2n) = 2J(n) + 1, n ≥ 1.$$
把这两个方程与 J(1) = 1 组合起来，就可以给出所有情况下定义 J 的递归式：
$$\left\{ \begin{array}{c} J(1) = 1 \\ J(2n) = 2J(n) - 1, n ≥ 1\\ J(2n) = 2J(n) + 1, n ≥ 1 \end{array} \right.$$

递归式地求解

有了递归式，我们可以计算出前几个解，看看能不能发现什么规律：

很容易注意到，可以按照 2 的幂将表中的数据分组，在每一组的开始 J(n) 都为 1，且组内数据每次递增 2。因此，递归式地解似乎可以写成这样：

$$J(2^m+l) = 2l + 1, m ≥ 0，n ≤ l ≤ 2^m \\ $$
$（注意，如果 2^m ≤ n < 2^{m+1}，则余下来的数 l = n - 2^m 满足 0 ≤ l < 2^{m+1} - 2^m = 2^m.)$

对于上式的证明，可以使用数学归纳法：当 m 为 0 时必然有 l = 0，于是 J(1)=1；下一步证明需要分奇偶分别讨论.
如果 m > 0 并且 $2^m + l = 2n$，那么 l 是偶数，故有

$$J(2^m + l) = 2J(2^{m-1} + \frac{l}{2}) - 1 = 2(2\frac{l}{2} + 1) - 1 = 2l + 1$$
这就证明了该公式在 $2^m + l = 2n$ 时是成立的。同理可证另一种情况也是成立的。

解的二进制表示

问题的每一个解都可以加以推广，使得它能运用于更加一般的问题，这是一件很有启发意义的事情。接下来，我们将对上诉递归式以及递归式地解进行推广，揭示所有这类问题背后所隐藏的结构。

在求解过程中，我们注意到 2 的幂起到了重要作用。一个很自然的想法就是研究 n 和 J(n) 的以 2 为基数的表示。假设 n 的二进制表示为：

$$n = (b_m b_{m-1} ... b_1 b_0)_2$$
也就是说，
$$n = b_m2^m + b_{m-1}2^{m-1} + · · · + b_12 + b_0$$
其中首位数字$b_m$为 1，注意到 $n = 2^m + l$，于是依次有：
$$n = (1 b_{m-1} b_{m-2} ... b_1 b_0)_2 \\ l = (0 b_{m-1} b_{m-2} ... b_1 b_0)_2 \\ 2l = (b_{m-1} b_{m-2} ... b_1 b_0 0)_2 \\ 2l + 1 = (b_{m-1} b_{m-2} ... b_1 b_0 1)_2 \\ J(n) = 2l + 1 = (b_{m-1} b_{m-2} ... b_1 b_0 b_m)_2$$
于是我们证明了
$$J(b_m b_{m-1} ... b_1 b_0)_2 = (b_{m-1} ... b_1 b_0 b_m)_2$$
用程序语言来说就是，n 左循环移动一位就得到了 J(n)！这真是不可思议！

另一个值得注意的现象是，如果重复进行循环左移，即重复运用 J 函数，会出现首位数字为 0 的情况，这种情况下数的位数将会减少，即首位 0 将会被丢弃。重复运用 J 会得到一列递减的值，它们最终会到达一个不动点。利用循环左移的性质不难发现，最后的不动点全由 1 组成，它的值为 $2^{v(n)} - 1$，其中 v(n) 是二进制表示中 1 的个数。
于是由于 v(13) = 3，有

$$\underbrace{J(J(...J}_{\text{2 or more}}(13)...)) = 2^3 - 1 = 7$$
类似地有
$$\underbrace{J(J(...J}_{\text{8 or more}}(101101101101011)_2...)) = 2^10 - 1 = 7$$
结果令人称奇，但准确无误。

成套方法

下一步我们要推广的递归式 J，看看在一般情况下形如递归式 J 的函数该如何求出一个封闭形式的解。
首先我们来构造一般情况下的 J 表达式，引入常数 α、β、γ

$$\left\{ \begin{array}{c} J(1) = α \\ J(2n) = 2J(n) - β, n ≥ 1\\ J(2n) = 2J(n) + γ, n ≥ 1 \end{array} \right.$$
类似约瑟夫问题的求解，我们首先对小的 n 值构造出如下的一般性的表：

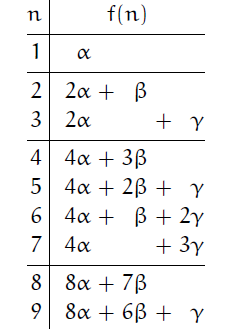
很容易发现这其中的规律。
如果把 f(n) 对 α、β、γ 的依赖关系分离出来，表示成如下形式：

$$f(n) = A(n)α + B(n)β + C(n)γ$$

根据一般性表我们可以猜测：

$$A(n) = 2^m \\ B(n) = 2^{m - 1} - l \\ C(n) = l$$
这里也有$n = 2^m + l$以及$0≤ l < 2^m (n ≥ 1)$
用归纳法证明上述猜想并不困难，但是计算起来比较复杂，这里介绍一个更好的方法，通过取特殊值，然后将它们组合起来。
考虑 α = 1、β=γ=0 这一特殊情况，此时递归式变为：
$$\left\{ \begin{array}{c} J(1) = 1 \\ J(2n) = 2J(n), n ≥ 1\\ J(2n) = 2J(n), n ≥ 1 \end{array} \right.$$
可知，$f(2^m+l) = 2^m$为真（对m进行归纳法）。
接下来，反过来使用一般递归式以及其一般解，从一个简单的函数 f(n)出发，研究是否有任何常数（α，β，γ）能定义它。
比如，将函数 f(n) = 1 代入有：
$$J(1) = α \\ 1 = 2*1 - β, n ≥ 1\\ 1 = 2*1 + γ, n ≥ 1$$
于是得到满足这些方程的值（α，β，γ）= （1，-1，-1）， 将给出 A(n) - B(n) - C(n) = f(n) = 1。类似的，也可以代入 f(n) = n 也能得到为一个（α，β，γ） = （1,0,1），于是有 A(n) + C(n) = n。这样一般递归式对每个 n 值都唯一的定义了 f(n)。
现在，我们证明了在一般情况解该一般递归式时，所得到的解中函数 A(n)、B(n)、C(n)满足方程：
$$A(n) = 2^m ; 当 n = 2^m + l 且 0 ≤ l < 2m\\ A(n) - B(n) - C(n) = 1 \\ A(n) + C(n) = n$$
于是解得
$$C(n) = n - A(n) = l\\ B(n) = A(n) - 1 - C(n) = 2m - 1 - l$$
这就证明了猜想
$$A(n) = 2^m \\ B(n) = 2^{m - 1} - l \\ C(n) = l$$
这一解题方法称为成套方法。成套方法的一般步骤是：寻求一组已知其解的通用参数，然后将特殊情况组合起来得到一般的情形，有多少个独立的参数就需要多少个独立的特解。

解的推广

上文以及证明了对于约瑟夫问题，可以用二进制表示巧妙的解决，那么对于推广的约瑟夫问题是否也存在相应的奇妙解法呢？
令 $β_0 = β，β_1 = γ$，推广的递归式就可以改写成：

$$f(1) = α \\ f(2n + j) = 2f(n) + β_j ( j = 0,1 ; n ≥ 1)$$
这个递归式按照二进制展开就是
$$f((b_m b_{m-1} ... b_1 b_0)_2) = 2f((b_m b_{m-1} ... b_1)_2)+ β_{b_0} \\ = 4f((b_m b_{m-1} ... b_2)_2)+ 2β_{b_1} + β_{b_0} \\ ...\\ = 2^mf((b_m)_2)+2^{m-1}β_{b_{m-1}}+· · ·+2β_{b_1} + β_{b_0}\\ = 2^mα+2^{m-1}β_{b_{m-1}}+· · ·+2β_{b_1} + β_{b_0}$$
如果解除二进制表示，允许使用任何数字，而不仅仅是0和1，则有
$$f((b_m b_{m-1} ... b_1 b_0)_2) = (αβ_{b_{m-1}}β_{b_{m-2}}· · ·β_{b_1}β_{b_0})_2$$
例如，当n = 100 = (1100100)2，原来的约瑟夫问题中 α = 1, β = -1, γ = 1，于是有

由于在n的二进制表示中每一块二进制数字(100...00)2 都被变换成

$(1-1...-1-1)2 = (0 0 ... 0 1)_2$
因而这就推出了循环移位的性质。
所以，改变表示法可以给出一般递归式更紧凑的解。
如果再进一步推广，对于更一般的递归式

$$f(j) = α_j ； 1 ≤ j < d\\ f(dn + j) = cf(n) + β_j ； 0 ≤ j < d ， n ≥ 1,$$
这里从基数为 d 的数着手，而产生的值用基数 c 来表示，它有变动基数的解：
$$f((b_m b_{m-1} ... b_1 b_0)_d) = (αβ_{b_{m-1}}β_{b_{m-2}}· · ·β_{b_1}β_{b_0})_c$$
这就是对该类递归式地通解。

感悟

① 改变进制看问题有时候会收获奇效。我们总是习惯于十进制，而现实中很多问题在十进制下很难看出规律，这个时候不妨转换一下进制，说不定规律会脱颖而出。
② 从一个普通的问题到一类问题，这是问题的抽象。对于解决抽象问题，它涉及到的方法一般都源于它的某一个具体问题。而从具体问题上升到抽象问题，然后寻找这类问题的通解，这往往能够揭示问题的本源。