推荐系统入门

数据挖掘

---

网络世界中，推荐系统应用很广泛，比如亚马逊的“看过这件商品的顾客还购买过”板块，还有网易云音乐的音乐推荐系统，这些都是对大数据的应用。这些算法的实现原理其实很简单，和数学的线性回归非常类似。

推荐系统的首要任务是要找到相似的用户，可以用简单的二维模型来实现，其中X,Y轴可以选取用户对某两件商品的评价（星级），通过计算用户之间的“距离”来表征相似度。

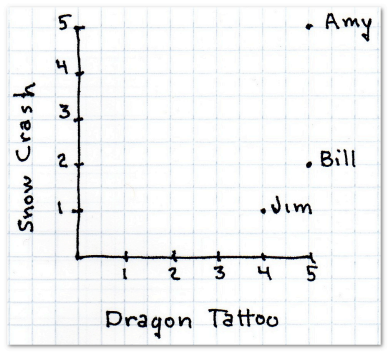
曼哈顿距离

这是最简单的距离计算算法。

$$d = |x_1 - x_2| + |y_1 - y_2|$$

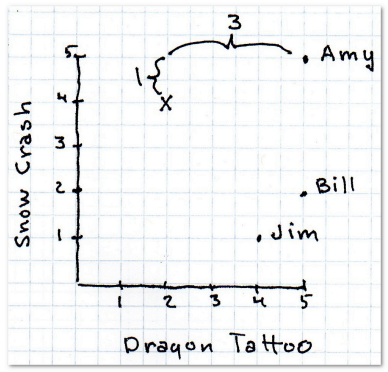
找到与该用户距离最近的用户，则认为这两个用户相似。

曼哈顿距离的优点之一是计算速度快，对于Facebook这样需要计算百万用户之间的相似度时就非常有利。

曼哈顿距离的python实现：

def manhattan(rating1, rating2):
    """计算曼哈顿距离。rating1和rating2参数中存储的数据格式均为
    {'The Strokes': 3.0, 'Slightly Stoopid': 2.5}"""
    distance = 0
    for key in rating1:
        if key in rating2:
            distance += abs(rating1[key] - rating2[key])
    return distance

欧几里得距离

$$d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$$
简单来说，就是利用勾股定理。

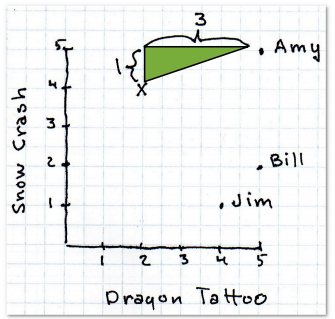
当然，这只是二维的，对于一个N维模型，可以利用以下公式：

$$d = (\sum_{k=1}^{n}{|x_k - y_k|^r})^{\frac{1}{r}}$$
这个距离又叫做闵可夫斯基距离
其中：

• r = 1 该公式即曼哈顿距离
• r = 2 该公式即欧几里得距离
• r = ∞ 极大距离

曼哈顿距离和欧几里得距离在数据完整的情况下效果最好，但是现实中缺失数据很常见，这样就会造成距离计算权重不同的偏差。

并且对于闵可夫斯基距离，有一个结论：
r值越大，单个维度的差值大小会对整体距离有更大的影响。

闵可夫斯基距离的算法实现：

def minkowski(rating1, rating2, r):
    distance = 0
    for key in rating1:
        if key in rating2:
            distance += pow(abs(rating1[key] - rating2[key]), r)
    return pow(distance, 1.0 / r)
# 修改computeNearestNeighbor函数中的一行
distance = minkowski(users[user], users[username], 2)
# 这里2表示使用欧几里得距离

皮尔逊相关系数

但是这里有一个问题，对于评分，不同用户有不同的标准，有人打分不会极端，都在2-4之间，有人打分都在4-5之间，而有人不是1就是4……
对于这种情况，解决办法之一是使用皮尔逊相关系数。
皮尔逊相关系数用于衡量两个变量之间的相关性，它的值在-1至1之间，1表示完全吻合，-1表示完全相悖。

皮尔逊相关系数的计算公式是：

$$r = \frac{\sum_{i=1}^{n}{x_iy_i} -\frac{\sum_{i=1}^{n}{x_i}\sum_{i=1}^{n}{y_i}}{n}}{\sqrt{\sum_{i=1}^{n}{x_i^2}-\frac{(\sum_{i=1}^{n}{x_i})^2}{n}}\sqrt{\sum_{i=1}^{n}{y_i^2}-\frac{(\sum_{i=1}^{n}{y_i})^2}{n}}}$$

计算皮尔逊相关系数的代码:

from math import sqrt
def pearson(rating1, rating2):
    sum_xy = 0
    sum_x = 0
    sum_y = 0
    sum_x2 = 0
    sum_y2 = 0
    n = 0
    for key in rating1:
        if key in rating2:
            n += 1
            x = rating1[key]
            y = rating2[key]
            sum_xy += x * y
            sum_x += x
            sum_y += y
            sum_x2 += pow(x, 2)
            sum_y2 += pow(y, 2)
    # 计算分母
    denominator = sqrt(sum_x2 - pow(sum_x, 2) / n) * sqrt(sum_y2 - pow(sum_y, 2) / n)
    if denominator == 0:
        return 0
    else:
        return (sum_xy - (sum_x * sum_y) / n) / denominator

余弦相似度

余弦相似度在文本挖掘中应用得较多，在协同过滤中也会使用到。
以iTunes为例，iTunes上有1500万首音乐，而对于一般人可能只听过几千首。所以说单个用户的数据是 稀疏 的，因为非零值较总体要少得多。当用1500万首歌曲来比较两个用户时，很有可能他们之间没有任何交集，这样一来就无从计算他们之间的距离了。
类似的情况是在计算两篇文章的相似度时。比如说想找一本和《The Space Pioneers》相类似的书，方法之一是利用单词出现的频率，即统计每个单词在书中出现的次数占全书单词的比例，如“the”出现频率为6.13%，“Tom” 0.89%，“space” 0.25%。可以用这些数据来寻找一本相近的书。但是，这里同样有数据的稀疏性问题。《The Space Pioneers》中有6629个不同的单词，但英语语言中有超过100万个单词，这样一来非零值就很稀少了，也就不能计算两本书之间的距离。
余弦相似度的计算中会略过这些非零值。它的计算公式是：

$$cos(x,y) = \frac{x·y}{|x||y|}$$
这个公式就是余弦公式。

选择何种相似度？

• 如果数据存在“分数膨胀”问题，就使用皮尔逊相关系数。
• 如果数据比较“密集”，变量之间基本都存在公有值，且这些距离数据是非常重要的，那就使用欧几里得或曼哈顿距离。
• 如果数据是稀疏的，则使用余弦相似度。

K最邻近算法

对于多个用户会推荐结果的贡献，可以使用相关系数确定他们的比重，通过加权得到最终的推荐占有比例。