基于隐变量的推荐模型

推荐系统

---

矩阵分解

上一篇介绍了协同过滤，其重点就是在人-物品矩阵上，其中心思想是去对人或者物品进行聚类，从而找到相似人或者相似物品，用群体的智慧为个人进行推荐，但是，这种近邻模型也存在好多问题：

1. 随着人和物品的增加，系统的推荐效果并不是线性增加的
2. 矩阵中元素稀疏，在计算过程中，随机的增减一个维度，对结果影响很大

为了解决上面的问题，于是就有人发明了矩阵分解的方法，矩阵分解简单讲看下面图：

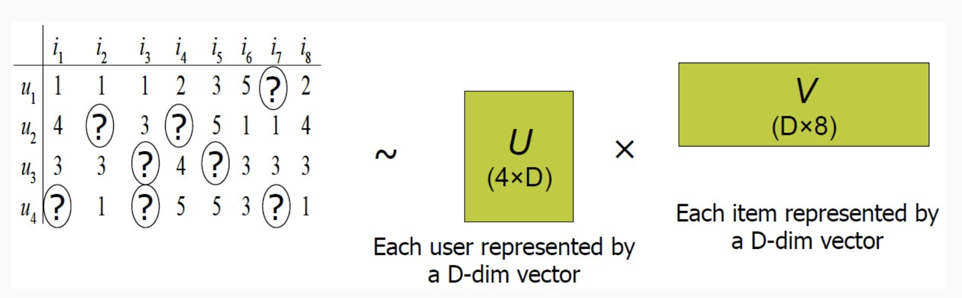
假设用户物品的评分矩阵 A 是 m 乘以 n 维，即一共有 m 个用户，n 个物品。我们选一个相对 m 和 n 很小的数 k，通过一套算法得到两个矩阵 U 和 V，矩阵 U 的维度是 m 乘以 k，矩阵 V 的维度是 n 乘以 k。

我们现在对上面的整个过程进行解释。

刚开始我们有用户-物品的矩阵，但是呢，整个矩阵中元素非常稀疏，也就是说我们所能得到的有效信息非常好，现在我们希望通过一定的方法来补全信息。

补全的方法呢就是模拟矩阵中元素的生成过程，此处我们假设矩阵中i,j位置处的元素是由一个用户向量 $u_i$ 和物品向量 $item_j$ 相乘得到，此处 $u_i$ 和 $item_j$ 有相同的维度， 我们称作用户和物品的隐向量，用数学描述就是：

$$r_{ij}=u_i item^T_j$$

矩阵分解求解方法

现在我们知道了分解原理，下一步就是如何去求解了，介绍两种方法，一种是梯度下降，另一种是交替最小二乘法 ALS。

我们先来看“梯度下降”（Gradient Descent）的方法，要用梯度下降来优化的话，我们需要先定义损失函数：

$$\underset{u_i,i_j}{min}\sum_{i,j}{(r_{ij}-u_iI_j^T)^2+\lambda (\left \| u_i \right \|^2+\left \| I_j \right \|^2)}$$
这个损失函数由两部分构成，加号前一部分控制着模型的偏差，加号后一部分控制着模型的方差。

接着我们来看交替最小二乘法 ALS，其原理是：先假设user矩阵的特征值，通过梯度下降求解item的特征值；再假定item的特征值，求解user的特征值，

上面我们对于用户的评分只建模了用户和物品的隐向量，但是实际中有一些用户会给出偏高的评分；有一些物品也会收到偏高的评分，甚至整个平台所有的物品的评分都会有个偏置，基于此，我们修正下我们的损失函数：

$$\underset{u_i,i_j}{min}\sum_{i,j}{(r_{ij}-u_iI_j^T-\mu - b_i - b_j)^2+\lambda (\left \| u_i \right \|^2+\left \| I_j \right \|^2 + b_i^2 + b_j^2)}$$

在加入了偏置信息的基础上，我们在加入引入用户的一些隐性行为，将这种隐反馈考虑进来，特别适合一直浏览，但是不怎么进行评价的用户。此时我们建模得到下面的式子：

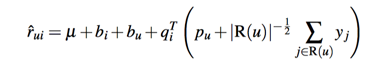
其中R(u)是用户u有隐性行为的item集合，y则是对item隐性行为的向量建模，如果用户有多个隐性行为，我们同样可以再加上一个隐向量：

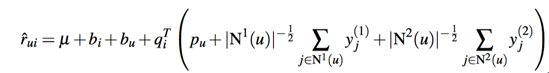
更多的关于这svd相关的，可以参考我之前的文章推荐系统算法之surprise实战，理解结合了代码，分析了不同的算法实现。

负采样

下面我们来讨论一个关于隐式反馈的问题，我们以浏览举例子，我们在收集用户浏览数据的时候，一般只有用户明确浏览了哪个物品的记录，一般没有用户明确不浏览哪个文档的记录，这就导致我们的训练样本中数据只有1个类别，因此我们需要一些负采样的手段，可行的方法有两个：

• 随机均匀采样，和正样本保持 1：1
• 按照物品热点采样，理论上这个物品很热门，用户都没有看，这个用户更加有可能是对这个物品真不感兴趣

现在我们已经通过负采样的方式得到了负样本了，下一步是我们在正样本的基础上加入置信度，这个置信度是通过统计用户浏览物品的次数得到，用户如果反复浏览，说明用户对这个物品就越感兴趣，所以我们假设

1. 用户没有浏览，分数为0（负采样得到）
2. 浏览一次，得分为1，随着浏览次数增加，得分提高

此时我们的损失函数为：

$$\underset{u_i,i_j}{min}\sum_{i,j}{c_{ij}(r_{ij}-u_iI_j^T)^2+\lambda (\left \| u_i \right \|^2+\left \| I_j \right \|^2)}$$
其中 $c_{ij} = 1+\alpha C$，是置信度，表示如果浏览次数越高，表示用户越感兴趣，其权重就越高。

现在假设我们已经计算出用户和物品的隐向量了，接下去我们就要去计算用户对所有物品的评分了，从中选择topk的做推荐，这在工程上就会面临一个计算量问题，在上一篇文章深入浅出推荐系统之简单推荐模型中，讨论协同过滤的时候就有讲过如何进行计算的问题，可以去查看下，其主要思想就是将计算用户对所有物品的评分拆分成了MapReduce任务，非常精妙，其大致原理如下：

现在总结下上面讲的隐向量模型，隐向量模型尝试建立从隐藏变量到最终预测值之间的关系，在前面介绍的矩阵分解中，我们的输入是用户id和物品id，然后通过矩阵分解的方法，我们得到了用户的隐藏向量和物品的隐藏向量。

分解机

上面这种方法的问题是：我们无法对用户和物品显性特征的建模，譬如我们已经得到了用户的用户画像，或者物品的物品画像，但是我们不能融合进入我们的模型，我们如果要对这些显性特征进行建模的话，一个可行的方案就是逻辑回归，于是有人就对矩阵分解和逻辑回归进行了结合，提出了"分解机"的模型.

分解机FM的基本原理是：不仅对显性变量建模，而且对显性变量之间的关系进行建模，在对显性变量关系建模的过程中使用了隐变量的方法。

另外分解机的一个优势是可以部分解决冷启动问题，因为即使没有用户的反馈数据，我们也能够通过显性变量来预测出一个评分来,更多的关于FM的资料可以看我之前的文章CTR 预估之 FM。

下面我讲下 "CTR 预估之 FM" 文章没有讲的内容，FM是如何能够融合协同过滤、矩阵分解和线性模型的优点的。

以下内容主要来自论文Factorization Machines with libFM.

先来看一张训练数据的图：

上面x是特征向量，y是用户的评分，我们可以看到用户向量中，对用户id和电影id都进行了one-hot编码，然后还加入了用户的历史行为和时间特征，此时的预测公式是：

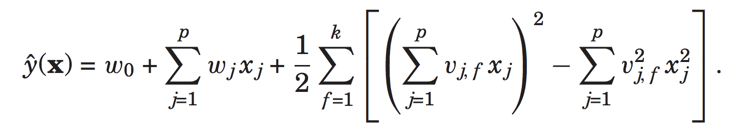
现在假设我们只有用户id和电影id这两个特征，则输入特征是：

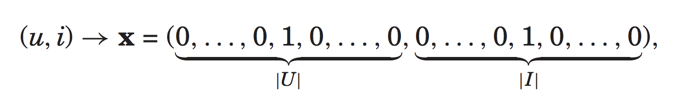
预测公式变为：

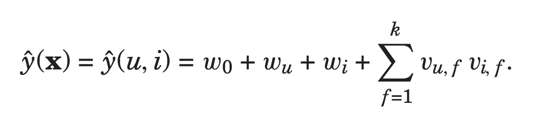
这不就是我们上面介绍的了加入了偏置信息的矩阵分解svd。

现在我们加入时间特征，则输入特征为：

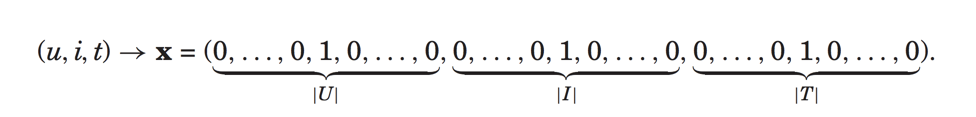
预测为：

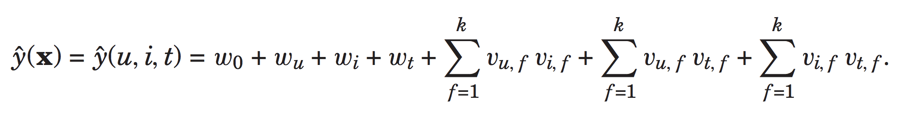
此时就变为了pairwise interaction tensor factorization model (PITF).

我们继续看一个复杂点的例子，我们有用户id和电影id，此时加入用户之前有过评分的电影 m
个，并且设置每个电影的权重为1/m，则此时有输入特征为：

预测为：

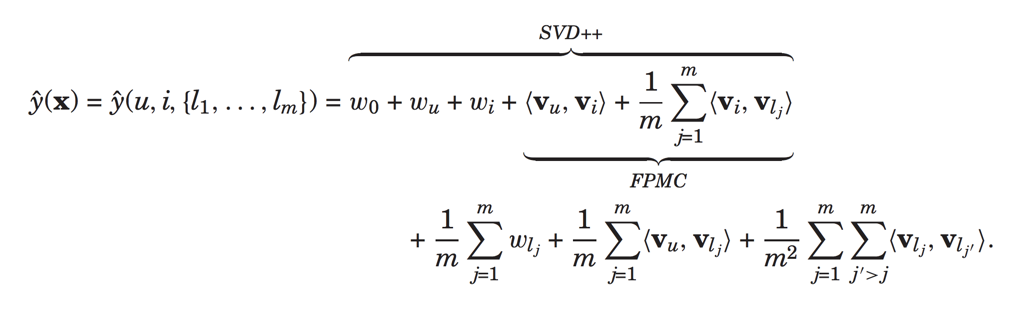
接着我们再来看不仅将用户的有过行为的电影建模进来，并且还将其对每个电影的评分特征加入，此时输入可以表示为：

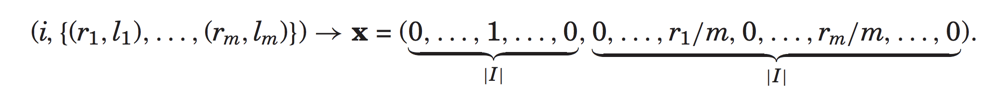
上面表示对于物品i，用户已经对于(l1,l2,...lm)的评分分别为(r1,r2,..rm)，
此时预测部分的物品相关为：

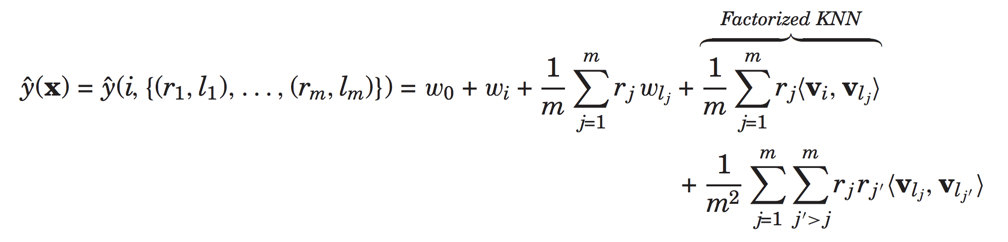
最后介绍一个对于用户属性特征的建模，输入特征为：

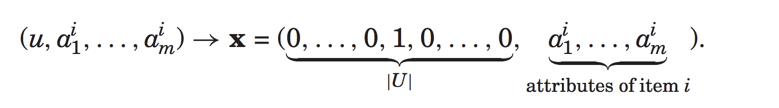
预测为：

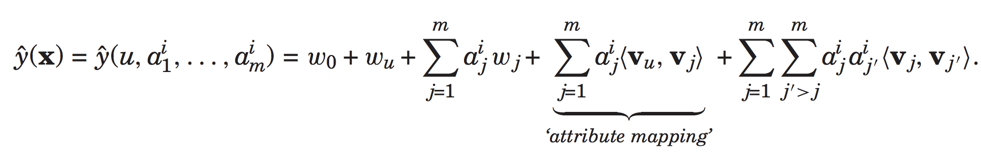
所以我们可以看到分解机FM真的是非常强大，能够通过一个模型融合协同过滤、矩阵分解和线性模型。

总结

本文介绍了基于隐变量原理两种算法：矩阵分解svd和分解机FM，其求解方法有：梯度下降和交替最小二乘法；在介绍完求解方法后，我们讨论svd的一些变种，以及集大成者FM是如何进行多模型融合的。

关于本文介绍的算法，我将会在GitHub上在腾讯的ad数据集上进行实现，欢迎持续关注。

你的鼓励是我继续写下去的动力，期待我们共同进步。