algorithms-on-graphs：graph basics 笔记三

algorithms-on-graphs

本文是学习 Algorithms on Graphs 的笔记第3篇。

Minimum spanning tree (MST)

最小生成树算法

树的特点

两种最小生成树算法

• Kruskal’s algorithm
• Prim’s algorithm

Kruskal’s algorithm 实现

Prim’s algorithm 实现

最短路径加速：Bidirectional Dijkstra

思路是我们如果单向搜索，其搜索面积显然大于双向搜索。
看下面的例子：

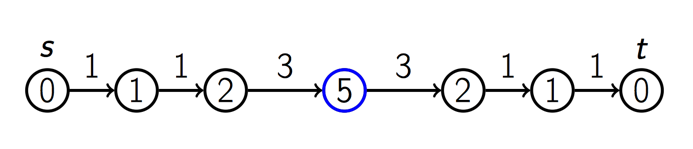
我们能够找到一个meeting vetex，但是我们可以说这是最短路径嘛？

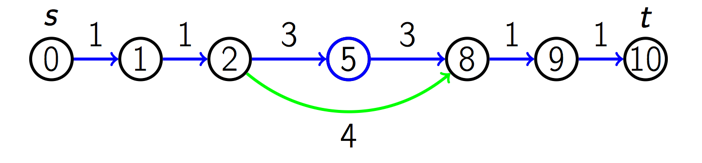
上面我们就发现了一条更短的路径。

那当我们找到一个交汇点后，怎么去寻找最短路径呢？看下面的定理：

上面定理说我们最短路径经过的点u，要么在forward和backward都处理过，要么只在其中一个处理过。

下面是证明不会出现在forward和backward都没处理的点中。

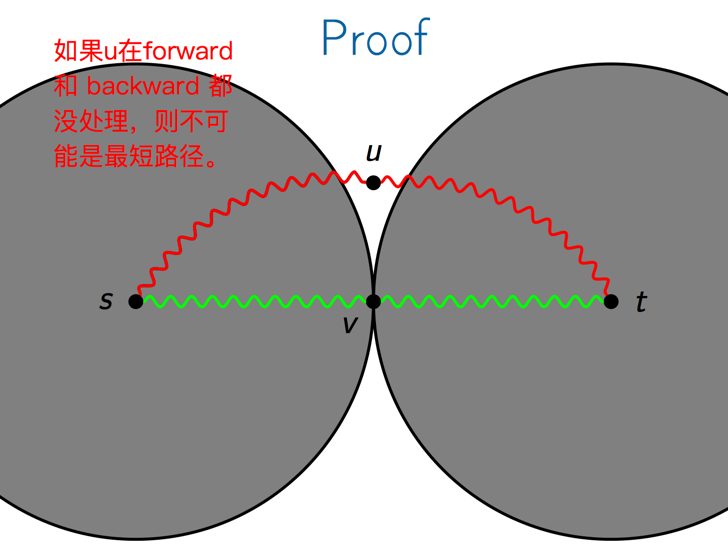
接着我们看如果点出现在forward中，会怎么样？

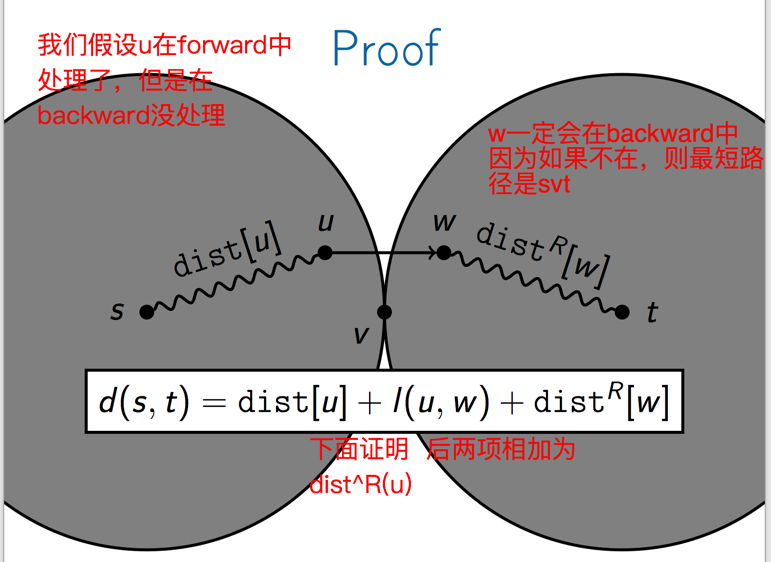
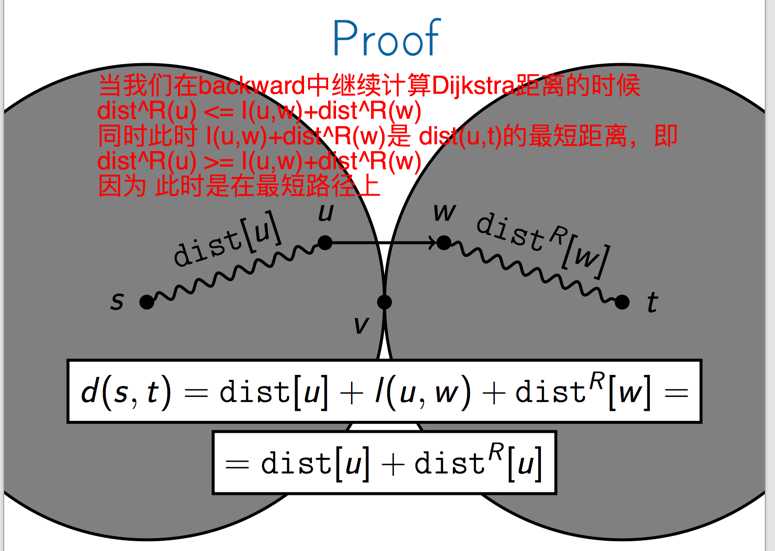
当我们在backward中继续计算Dijkstra距离的时候dist^R(u) <= I(u,w)+dist^R(w)
同时此时 I(u,w)+dist^R(w)是 dist(u,t)的最短距离，即 dist^R(u) >= I(u,w)+dist^R(w)
因为 此时是在最短路径上

下面是具体的算法描述：

A-star Algorithm (A * )

下面介绍另一种最短路径算法：A-star Algorithm。

A-star 的一个思想是：如果我们知道了一个搜索方向，能够帮助我们更快的找到最优路径，看对比图：
双向搜索：

有方向搜索：

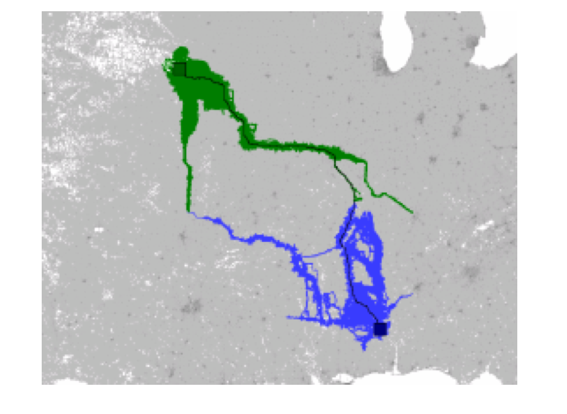
先给出一个定义：

根据新的边的weights定义，我们有下面的定理：


上面这个定理的意义是：如果我们在原空间中找到最短路径，在新的空间(对边权重重新通过函数pi定义）中也是短路径。

下面我们具体介绍下A*算法：A* ≡ Dijkstra

Bidirectional A *

Lower Bounds

Euclidean Potential

总结

本文是对 Algorithms on Graphs 第5-6周 课程的一个记录，笔记更多的是给自己复习时快速查阅用。

你的鼓励是我继续写下去的动力，期待我们共同进步。