Cyclical Learning Rates for Training Neural Networks

论文笔记 lr

增加lr短期可能会让loss增大，但是长期来看对loss减少是有帮助的。基于上面的观察，我们有别于传统的lr指数下降，我们采用周期性调整的策略，一种最简单的方式叫Triangular learning rate policy：

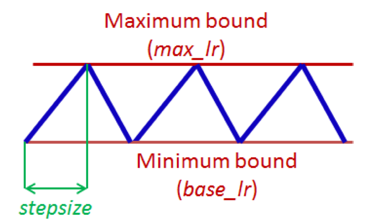
为什么这种周期性变化的lr策略有效呢？
我们可以见知乎的一个问答有哪些学术界都搞错了，忽然间有人发现问题所在的事情？

长期以来，人们普遍认为，的神经网络中包含很多局部极小值（local minima），使得算法容易陷入到其中某些点，这是造成神经网络很难优化的原因，但是到 2014 年，一篇论文《Identifying and attacking the saddle point problem in
high-dimensional non-convex optimization》指出高维优化问题中根本没有那么多局部极值。作者依据统计物理，随机矩阵理论和神经网络理论的分析，以及一些经验分析提出高维非凸优化问题之所以困难，是因为存在大量的鞍点（梯度为零并且 Hessian 矩阵特征值有正有负）而不是局部极值。

因此在鞍点附近增加lr，能够让我们快速跳出鞍点。有篇中文博客SGD，Adagrad，Adadelta，Adam 等优化方法总结和比较描述了现在各种方法在鞍点附近的优化，看图：

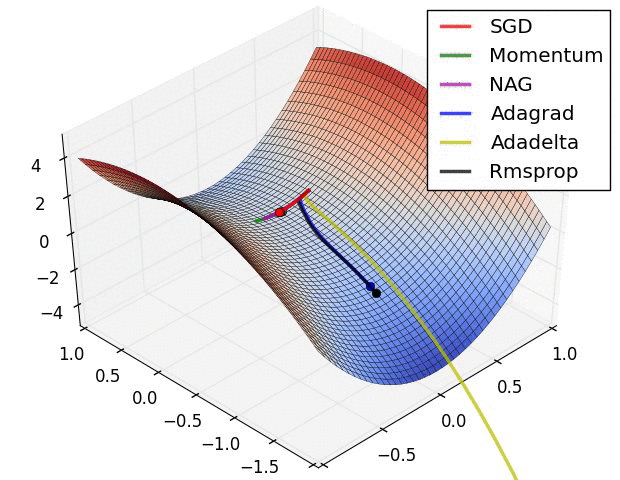
下面回到论文，前面论文介绍了一种方法叫：triangular，

里面需要我们确定的参数有：stepsize，base_lr,max_lr，下面我们来看step_size怎么选取？

假设有5w个训练样本，batchsize=100，则每个epoch有500次迭代，实验结果表明stepsize设置为2~8倍的迭代次数比较合适。

使用 triangular 策略还给我们带来的一个好处是我们可以知道什么时候停止训练：我们可以采用周期性的lr进行训练3回，然后再继续训练4次甚至更多，能够达到很好的效果。

下一步我们需要回答的是怎么去选择 base_lr,max_lr 两个参数。

方案：设置 stepsize 和 max_iter 为一个 epoch 中迭代次数，然后 lr 从 base_lr 增大到 max_lr ，然后画出 accuracy 在此过程中的变化曲线。

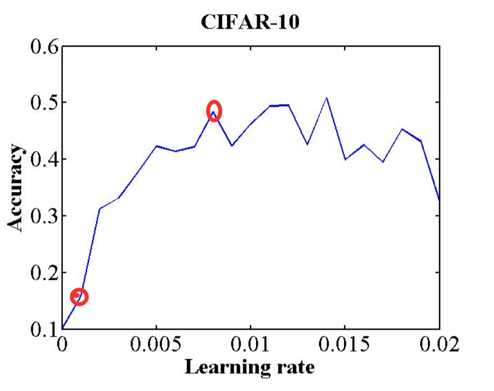
如上图，我们找寻base_lr和max_lr的方式是：accuacy 开始剧升的时候是一个点，accuacy 开始下坡的时候是一个点。

下面来看一个GitHub上对于此论文的实现.

triangular

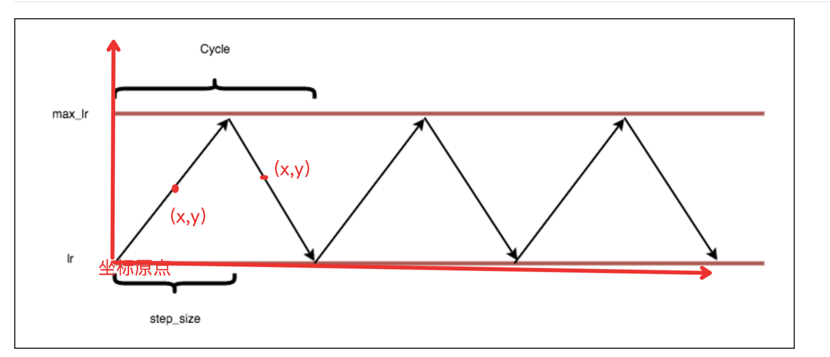
当前迭代次数属于哪个 cycle 中：

cycle = np.floor(1+iterations/(2*step_size))

下面是想计算上图中每个点其具体的lr值是多少，建立坐标后，开始计算点(x,y)，我们知道了当前cycle，每个cycle的iter是 2*cycle*step_size，然后再用当前 iterations 减去这个值：

x = np.abs(iterations/step_size - 2*cycle + 1)

y要区分是上升还是下降阶段：

lr = base_lr + (max_lr-base_lr)*np.maximum(0, (1-x))

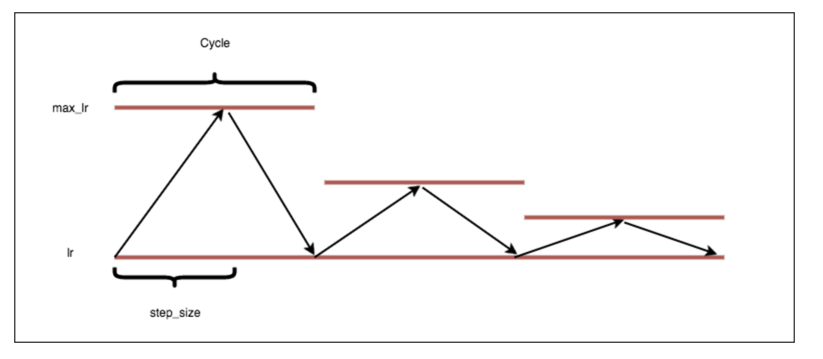
triangular2

这个策略是每个新的cycle，新的max_lr都减半：

exp_range

这个策略是每个新的cycle，新的max_lr指数下降：

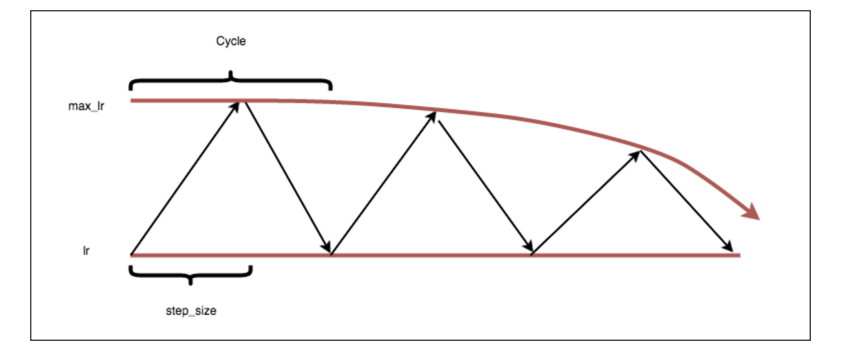
几个相关资料：
深度学习论文 - Cyclical Learning Rates for Training Neural Networks

手把手教你估算深度神经网络的最优学习率（附代码 & 教程）

bckenstler/CLR keras实现