algorithms-on-graphs：graph basics 笔记二

algorithms-on-graphs

本文是学习 Algorithms on Graphs 的笔记第2篇。

Paths && lengths

路径长度

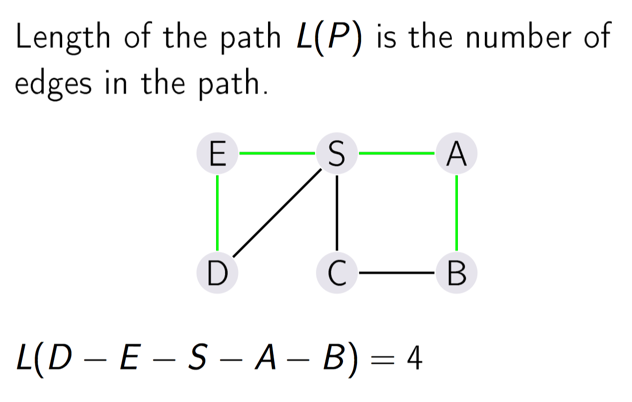
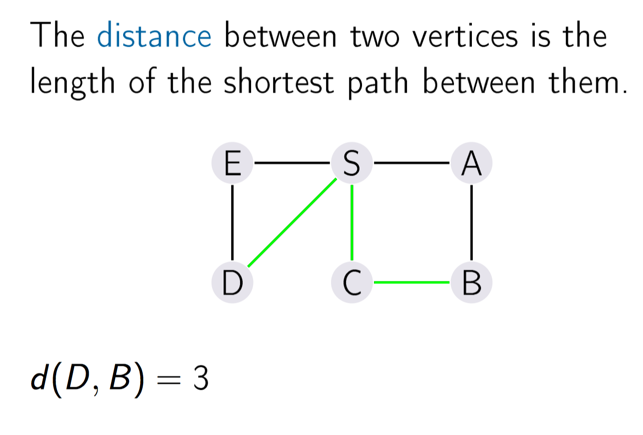
无向图两点距离

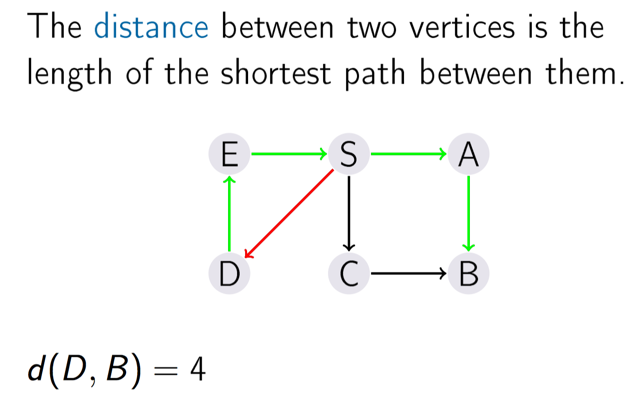
有向图两点距离

下面定义 distance level

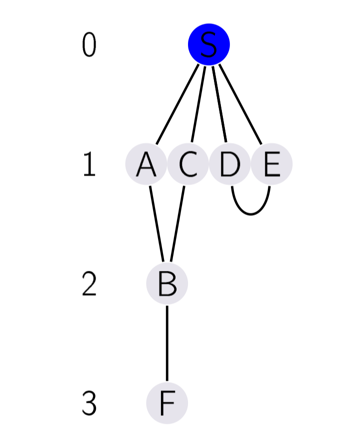
以s为起点，根据距离s不同分level。
下面是有向图的 distance level

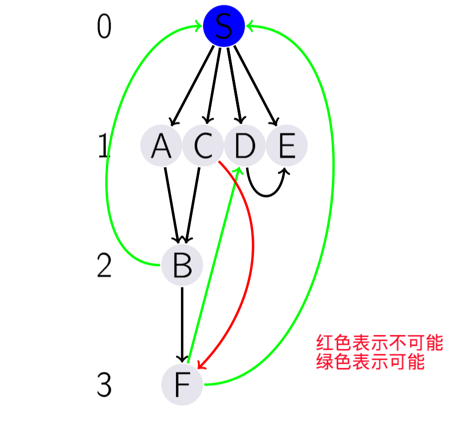
Breadth-first Search

时间复杂度

最短路径树-shortest-path tree

Fastest Route

上面介绍了无权重图中任意两点的最短路径，下面介绍有向图中任意两点的最短距离。
我们先给出一个观察：

最优路径上的子路径也是最优的，因为如果子路径不是最优的，就能将子路径替换为另一条最优子路径，此时就不满足最优子路径的假设了。

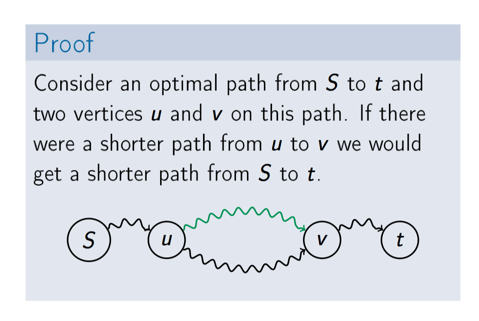
因此我们就有下面的结论：

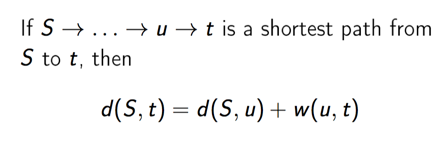
下面定义 Relax 操作：

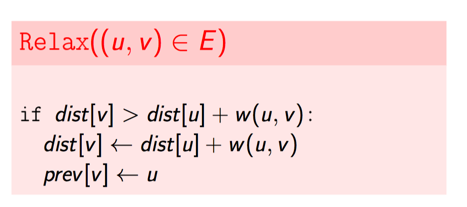
意义是检查边(u,v)是否会缩短到达v的最短距离。

下面我们定义

通过Naive操作，所有的最短路径就都算好了。

上面描述中，怎么能高效的relax all edges就是关键，下面介绍 Dijkstra's 算法。

Dijkstra's Algorithm

Dijkstra's 算法主要思想：

算法流程

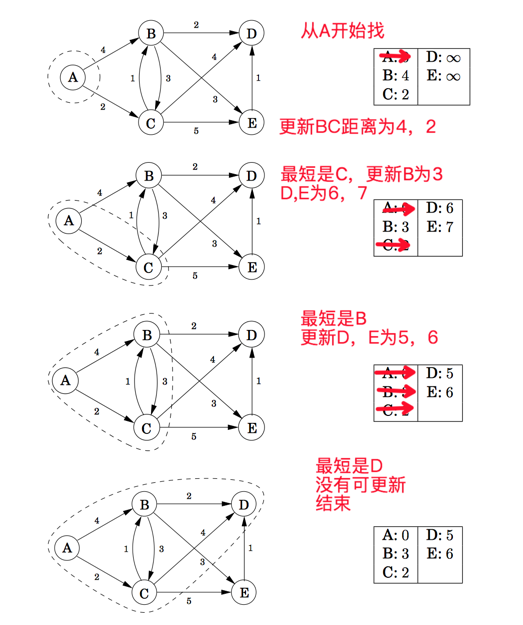
一个案例

最短乘积问题

问题描述:有5种货币，彼此之间的汇率如下，我们希望最大化转换：

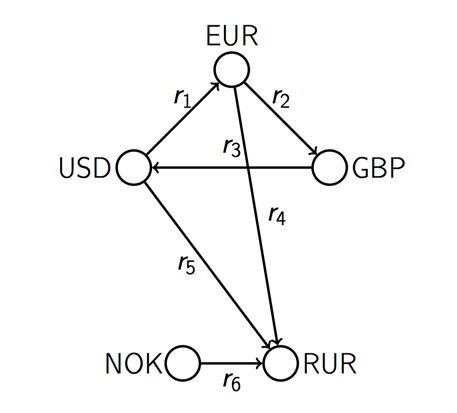
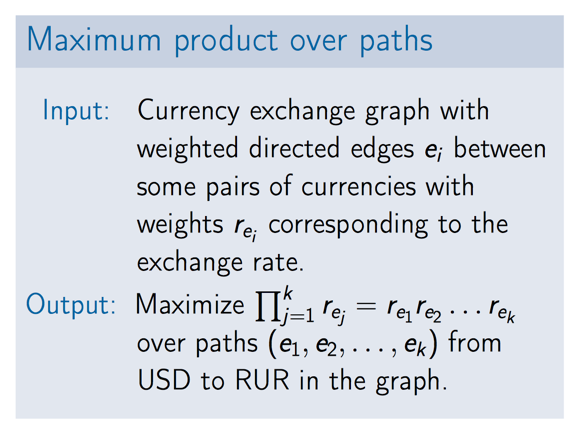
思路

• 将乘积通过log转换为加
• 通过加负号将max变为min

but上面的一个问题是，我们如果用 Dijkstra 算法，其要求权值为正，此处log后会出现负数，所以不满足Dijkstra算法的要求了。
下面是出现负环的时候问题

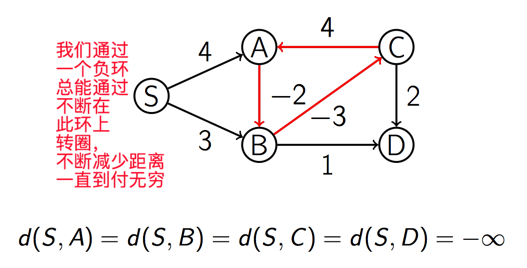
那怎么办？我们回到之前的Naive算法，通过不断relax edge的方式，于是就有了下面的方法：

举个例子来说明上面的过程

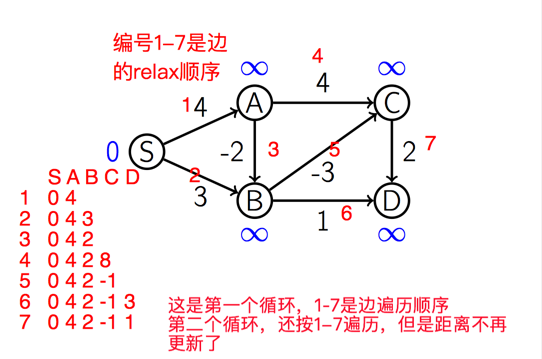
为了证明上面方法的正确性：为什么循环V-1次后，我们就能找到所有的最短路径了？
我们先给出一个引理：

在第K个循环relax后，最短路径至多包含k条边。

采用数学归纳法：

• k=0时，dis[S]=0，最短路径只有0条边
• 假设k次循环后，最多包含k条边，对于S->u的最短路径，我们能找到另一条边(v,u)，我们此时来对 (v,u)做 relax操作，则如果dis[u] > dis[v] + w(v,u)，则我们将边(v,u)加入到 S->v中，此时S->v最多有k条边，加上 (v,u) 后，最多就k+1条边，所以定理成立。

于是我们有下面的两个推论：

总结

本文是对 Algorithms on Graphs 第3-4周 课程的一个记录，笔记更多的是给自己复习时快速查阅用。

你的鼓励是我继续写下去的动力，期待我们共同进步。