algorithms-on-graphs：graph basics 笔记一

algorithms-on-graphs

本文是学习 Algorithms on Graphs 的笔记。

图表示

邻接矩阵

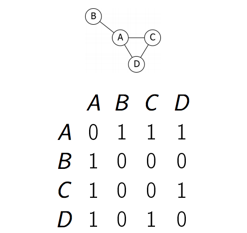
邻接表

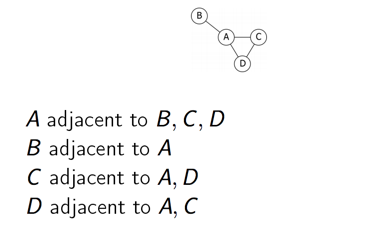
边链表

不同的表示方式决定了不同操作的时间复杂度。

图遍历

问题：我们怎么能够找到A能够达到的所有顶点？

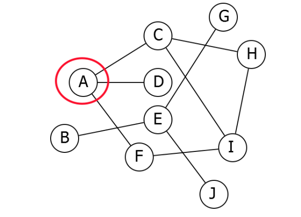
算法描述：

上面的算法还需要解决两个问题：

1. 怎么记录哪些边/顶点已经访问过了？
2. 以什么顺序来访问新加进来的顶点？

我们可以通过一个map来记录顶点是否访问过，而对于新增的顶点，我们采样深度优先的方案，一直访问下去。

DFS
如果我们要访问图中所有的点，方法如下：

Previsit and Postvisit Functions

我们在explore节点的时候，加上 Previsit 和 Postvisit 功能：

根据这个功能我们就可以实现一个时钟:

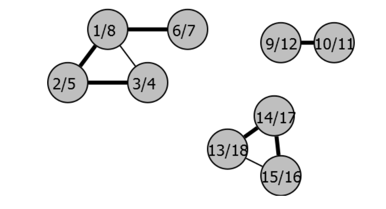
连通性

问题

我们可以通过修改DFS来做

可视化dfs地址

Directed Acyclic Graphs 有向非循环图

定义：

A source is a vertex with no incoming edges.
A sink is a vertex with no outgoing edges.

现在我们的目标是找到一个 Linear Ordering，什么叫 Linear Ordering，看下图：

怎么找呢？根据 sink 的概念，我们先去找 sink

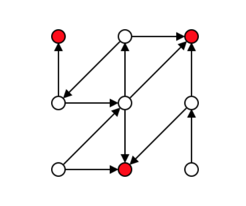
整个过程如下：

• Find sink.
• Put at end of order.
• Remove from graph.
• Repeat.

整个算法如下：

具体来说就是先按 DFS 访问图，然后再根据 Postvisit clock 排序从大到小就是我们需要求的值。
因为 DFS 总是一直走到最深处，即先找到 sink 为0的节点。

Strongly Connected Components

在无向图中有联通一说，在有向图中会更复杂点

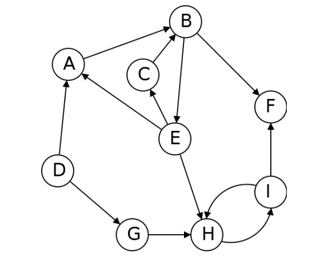
定义



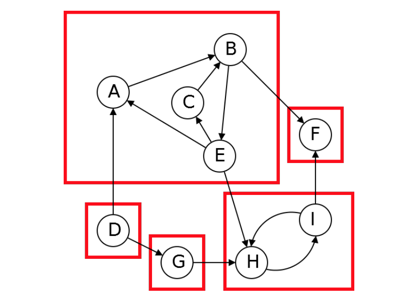
在有向图中，联通意味着集合里的点都能互相到达，画到一起就是下面这样子：

叫做 metagraph ，也是一个 DAG。

下面我们来描述如何计算一个SCC（Strongly Connected Components）。

SCC计算

简单算法

另一种思路是跟找 sink 节点一样，此时我们找一个聚合的 sink。
，但是怎么找到呢?

在无向图中，我们对 postOrder 进行排序，postOrder 小的就是 sink，在有向图中，我们有下面的理论：

因此有大的 postOrder 的是 source ，但是我们需要的是 sink，因此我们可以做如下操作：

下面我们开始给出具体的算法。

基本算法

上面做法就是不断通过DFS遍历，然后找到postOrder最大的顶点，从他开始找到所有能达到的点，然后删除，不断重复。

下面是一个改进算法，不用每次都dfs：

总结

本文是对 Algorithms on Graphs 第1-2周 课程的一个记录，笔记更多的是给自己复习时快速查阅用。

你的鼓励是我继续写下去的动力，期待我们共同进步。