神经网络基础知识

dnn

神经元

神经元的基础---线性分类器形式如下，

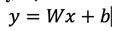
我们可以调整参数/权重W，使得映射的结果和实际类别吻合，而损失函数用来来衡量吻合度。

来看最简单的感知器：

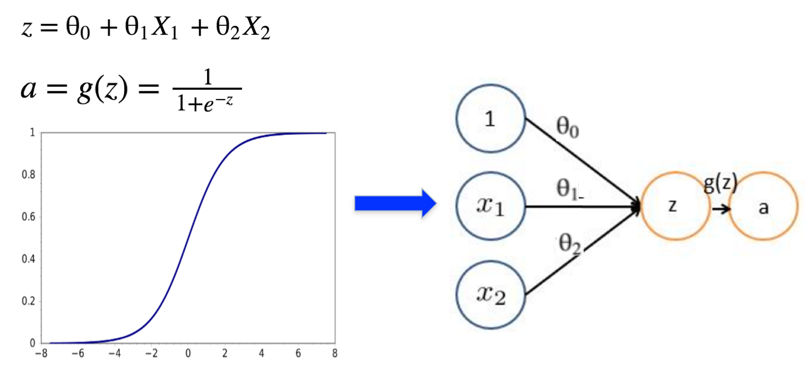
此处激活函数用sigmod。

简单的逻辑操作：and 和 or

我们可以用简单的感知器来完成逻辑与操作：

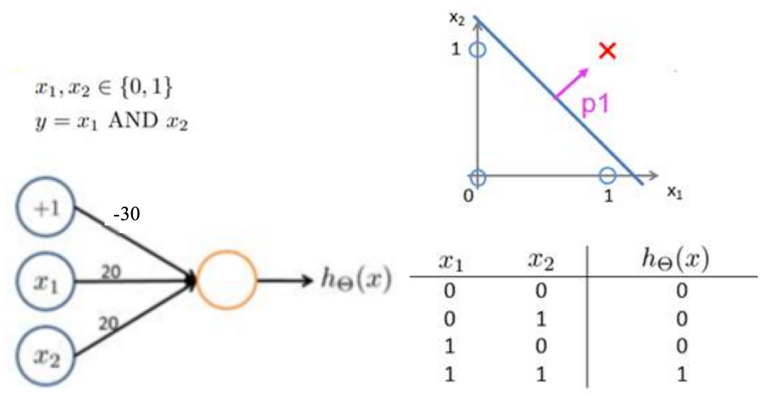
也可以完成逻辑或操作：

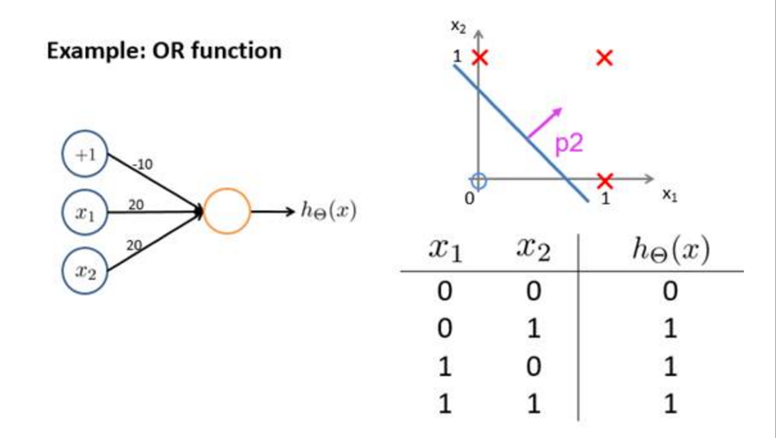
上面两个操作其数据集合都是线性可分的，有了上面两个操作后，我们就能进行一些逻辑组合了，看下面的and组合：

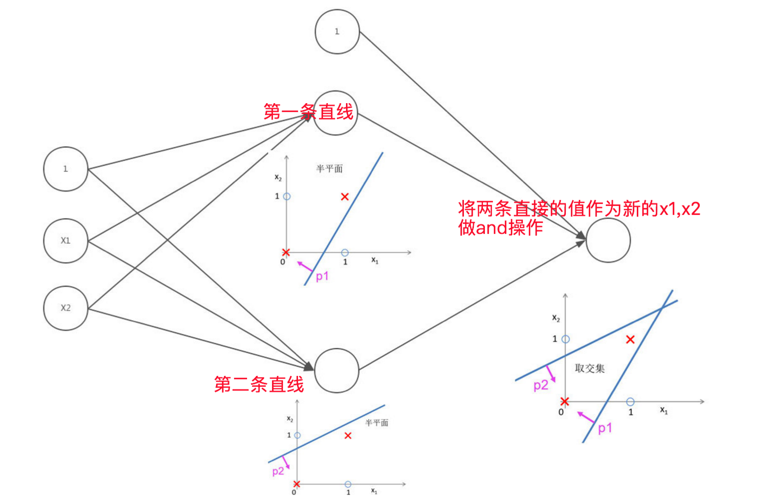
再来一个复杂的例子：

所以神经网络的能力是非常强大的。

有了上面介绍的and和or的能力后，我们来看下常见的简单神经网络，其能力极限在哪？

最简单感知器，可以将平面一分为2，如下图：

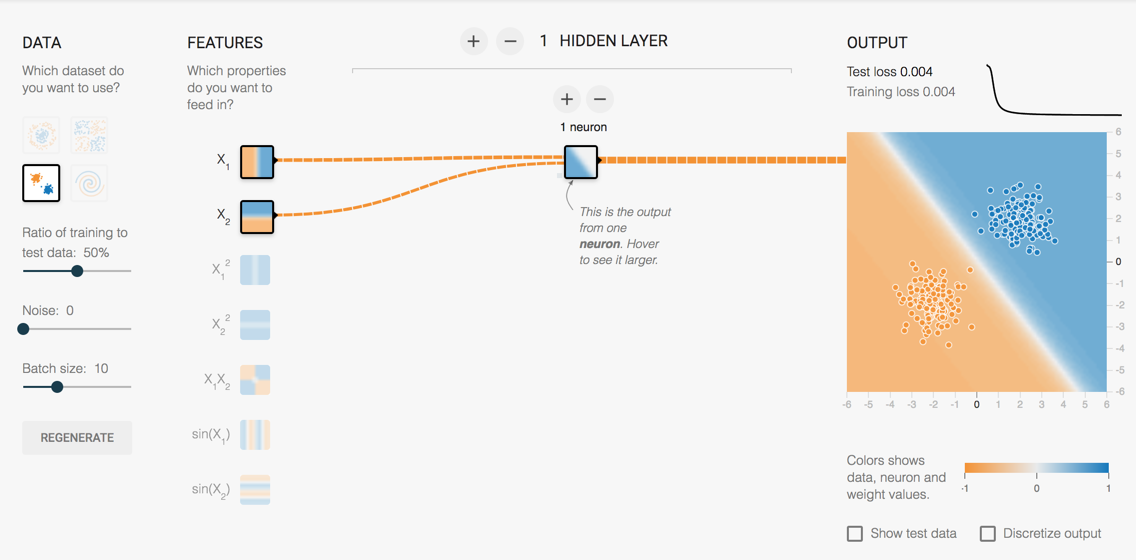
单隐层，其相当于做两条曲线的与操作，极限如下图：

此时如果我们增加中间隐层节点的个数，其实是可以画更多的曲线，从而达到任意的曲线性状，如下图：

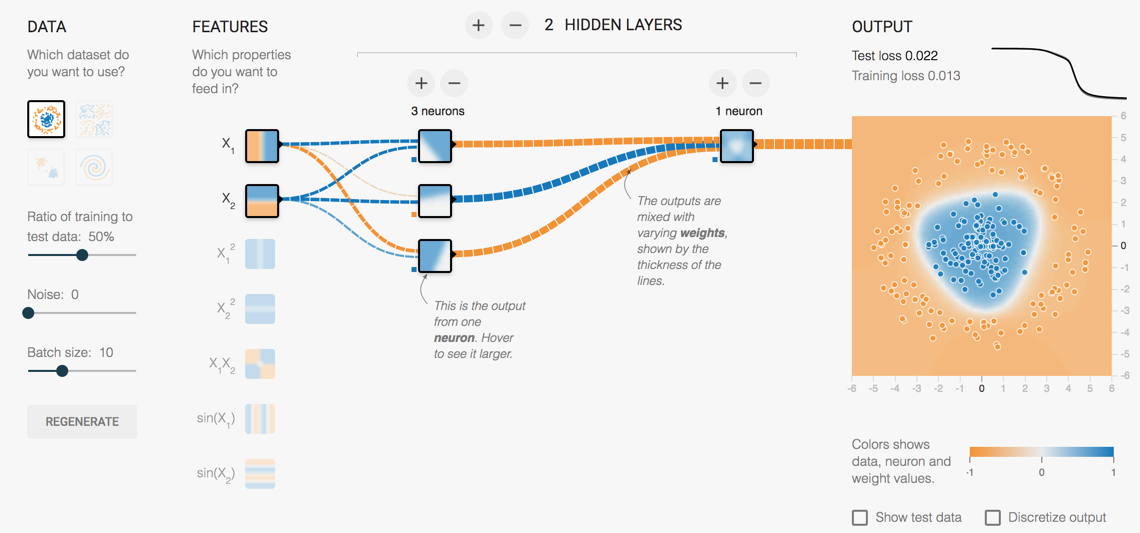
基本通过3个隐层神经元，3条直线就能达到要求了。
注：以上3张图片来自 http://playground.tensorflow.org/

下面总结下神经网络的表达能力：

• 理论上dnn可以逼近任何的连续函数
• 虽然只要隐层的神经元个数足够多也能达到和多隐层一样的数学效果，但是工程上还是多隐层好
• 对于一些分类数据（比如CTR预估里），3层神经网络效果优于2层神经网络，但是如果把层数再不断增加(4,5,6层)，对最后结果的帮助就没有那么大的跳变了
• 图像和音频处理比较特殊，需要更深的网络，这样子能更准确的提取图像、音频信息

BP算法

我们定义目标函数f和损失函数J：

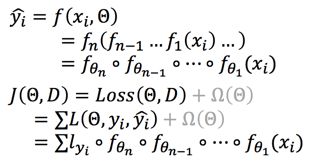
我们的目标是优化J，使得J最小，对J求每个theta的导数：

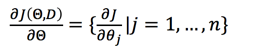
下面我们对上面式子展开：

于是整个计算过程如下：

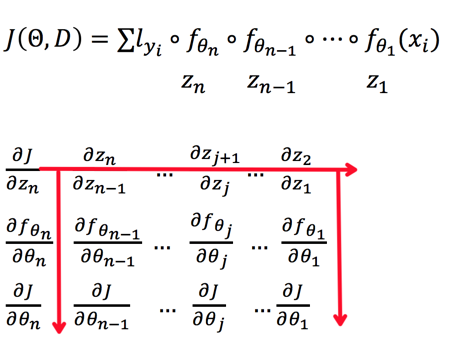
下面是常见函数的一些导数:

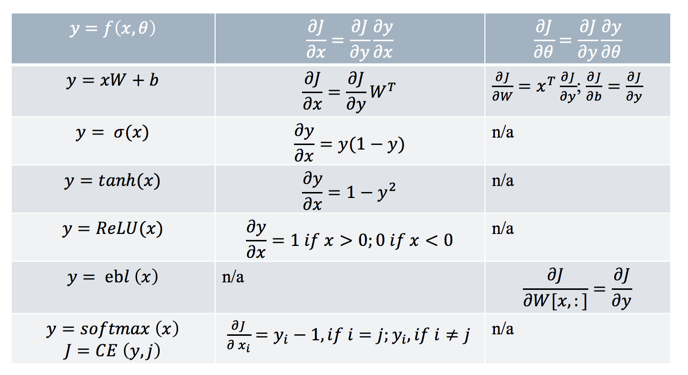
上面第二列是我们的输出对输入的导数，而第3列是输出对参数的导数。

ps:此处有个特别不好理解是embedding层的工作原理。
embed层在实现上其实就是通过lookup操作完成，怎么讲呢？
假设embed层是一个5*5的矩阵，则输入是index，0-4之间，输出则是一个行向量，代码实现：

def lookup(w,i):
    return w[i]

那更新梯度的时候怎么算呢？可以看代码:

def d_lookup(djdy,w,i): #此处djdy y是embed的输出
    djdw = np.zeros_like(w)
    djdw[i] = djdy
    return djdw

来看一个具体网络更新例子，网络结构如下：

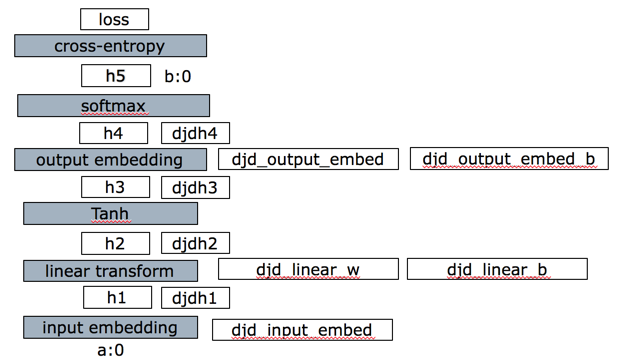
代码github地址

总结

本文介绍了神经网络的入门知识，从逻辑运算的角度去理解神经元，知道了其实复杂的函数都可以通过简单的逻辑与和或完成，接着介绍了基础的反向传播（BP）算法。

这是 深度学习系列 的第一篇，你的鼓励是我继续写下去的动力，期待我们共同进步。