如何手推“支持向量机”

机器学习 svm

---

0.前言

本文只讲述支持向量机（svm）的基础，不涉及任何高深东西。

1. 支持向量机 作用

先看一图：

我们第一直觉就是在两堆点中间画一根线，分开两类点。

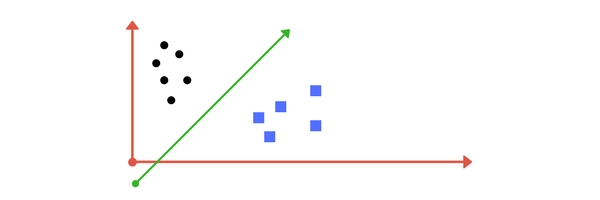
2. 如何判断好坏

下面问题来了，能够区分两堆点的线有好多，怎么区分哪个好？
这就引出了街宽(margin)的概念:

上面两条曲线，我们可以用下面的两个公式表达：

此处我们为什么选择常数1？因为如果假设是常数k，我们总可以通过两边同时除以k，对w和b进行缩放，让等式右边变为1.

上面两个式子可以统一为：

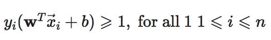
下面我们来计算街宽：

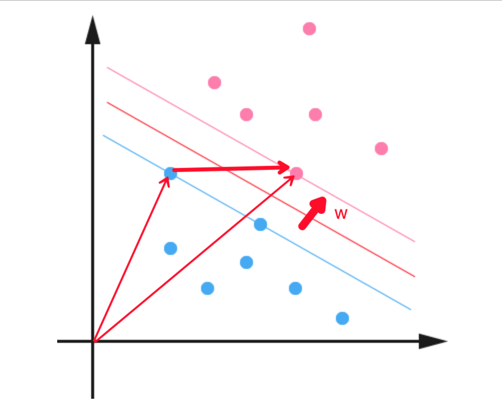
我们通过下面公式来计算街宽。

$$(x_+ - x_-)* \frac{w}{||w||} = (wx_+-wx_-)* \frac{w}{||w||} =(1-b- (-1-b)) * \frac{w}{||w||} = 2 * \frac{1}{||w||}$$

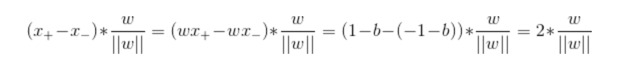
3. 优化街宽

我们现在知道街宽只和w相关，下面是我们的优化目标：

$$max \frac{1}{||w||} => min \frac{1}{2} ||w||^2$$
此时所有(x,y)满足：

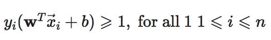
4. 最优解

总结下目前的优化目标：

我们通过拉格朗日可以将其转换为下面的求极值问题：


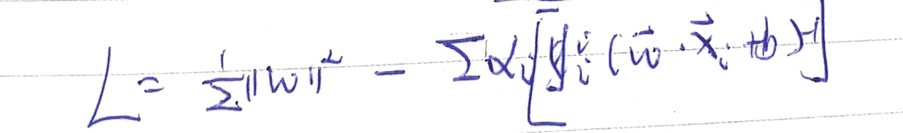
推导到这里，我们可以通过一些数学的工具包解出$\alpha_i$来。
当我们求出$\alpha_i$后，我么就能将w,b带回原来的式子，得到：

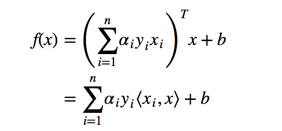
5. 支持向量

支持向量机中中一个很重要的概念就是支持向量，让我们来看上面推导中的式子：

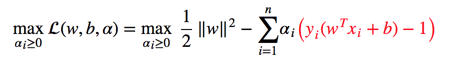
上面红色部分，对于那些不在“站街”上的点，其值肯定是大于0的，因此为了取得最大值，最好的方式就是让$\alpha_i=0$，因此我们在判断式子中，只需要计算$\alpha_i!=0$的那些$x_i$和新加入点x的点积即可。

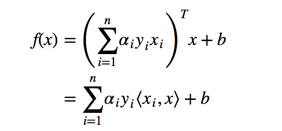
一个形象说明：

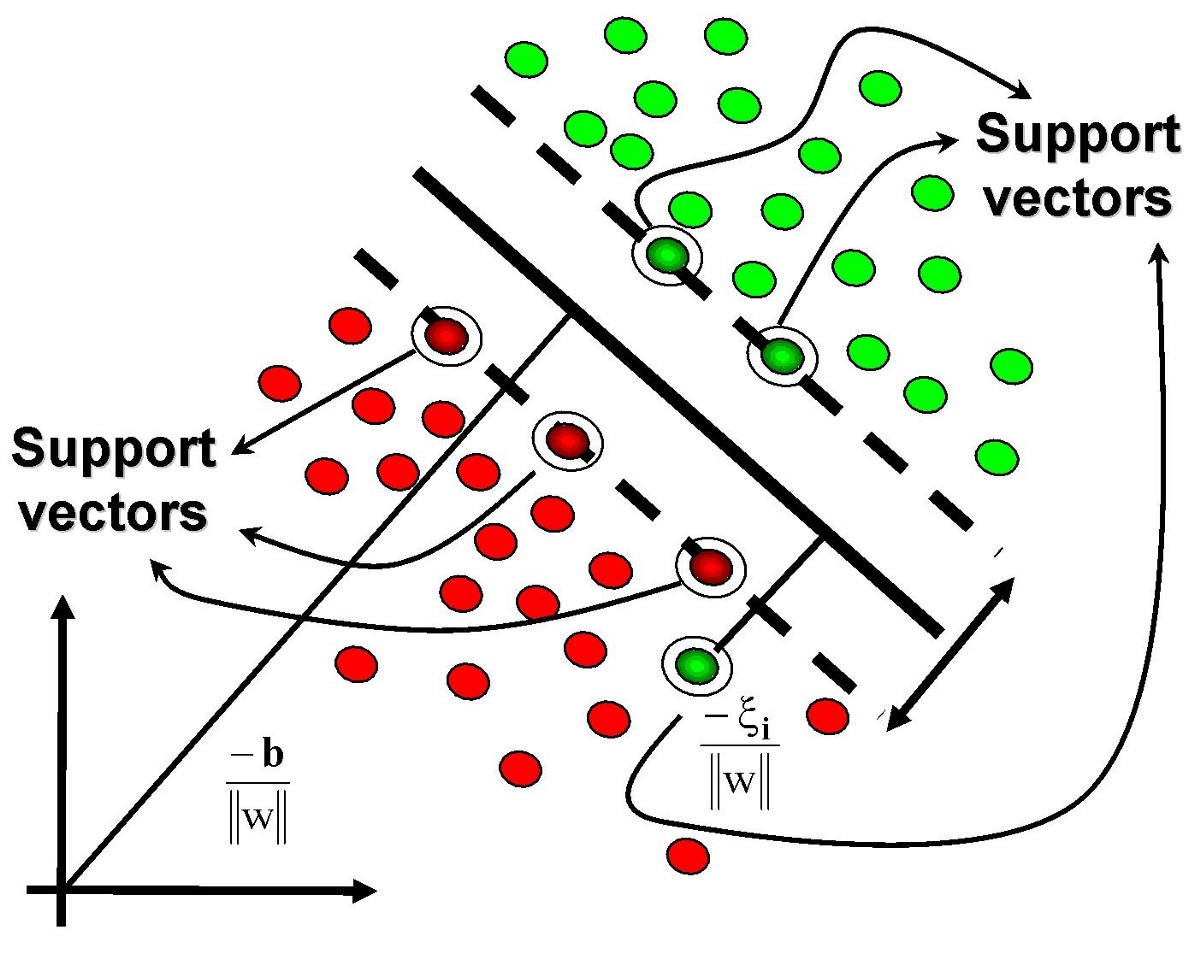
6. 核函数

线性空间到非线性空间变化，从而使得数据线性可分：


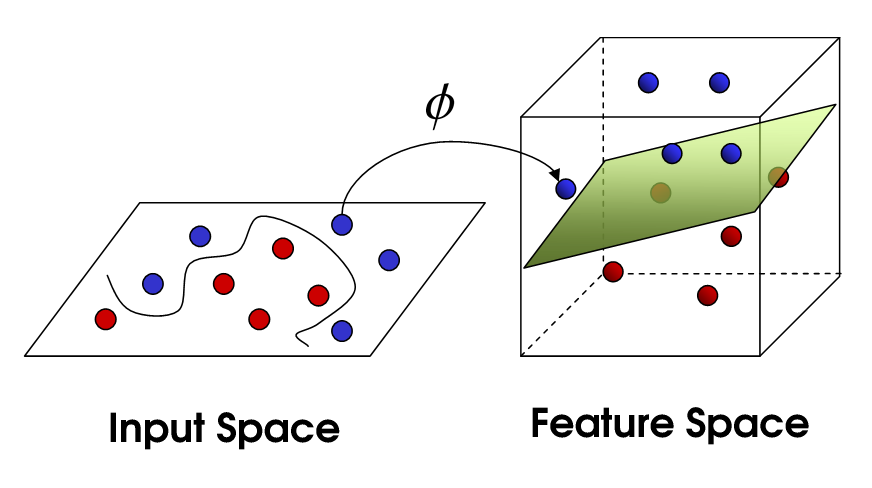
核函数的意义在于：我们不需要知道具体的映射函数是什么[由于太复杂我们也求不出😢]，我们只需要知道在新的空间中两个点之间的点乘形式即可😊。

7. 离群点处理

在前面的讨论中我们都假设数据是线性可分的，对于在原空间中不可分的点，我们通过核函数变化，也能在新空间中进行区分，但是由于噪声存在的原因，总会有些点偏离正常的点，我们称之为离群点，下面我们来定义下处理离群点的方案：

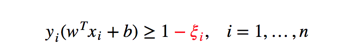
即在每个点的街宽上强制的留点余地：

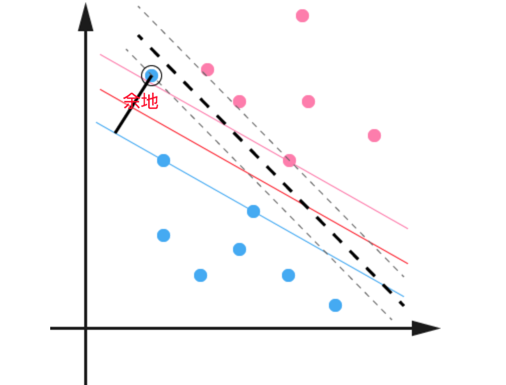
加上余地有优化目标变为：

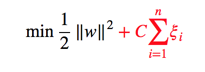
然后通过和上面一样的方法，我么能最终转换为下面的问题：

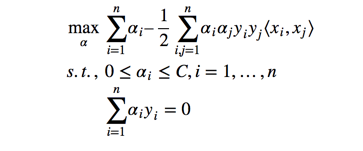
和之前的结果对比一下，可以看到唯一的区别就在每个 α 多了一个上限 C 。

8. 总结

本文介绍了支持向量机的作用，一步一步推导了支持向量机的求解过程了，接着给出了“支持向量” 的概念，最后介绍了核方法和离群点处理方法来解决非线性可分数据的分类问题。

9. 参考

支持向量机系列

你的鼓励是我继续写下去的动力，期待我们共同进步。