主题模型：LDA 数学基础

文本挖掘 机器学习

本文是我介绍Gibbs采样在LDA中运用的数学基础，关于LDA的Gibbs采样可以看文章贝叶斯推断：Gibbs sampling

数学基础

这些数学知识知道就好，我也不去深究里面的具体的推导、过程。

推荐一个特别好的数学文章，一克镭头条号，里面生活中的概率论写的真好。

Γ函数


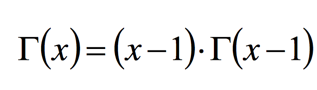
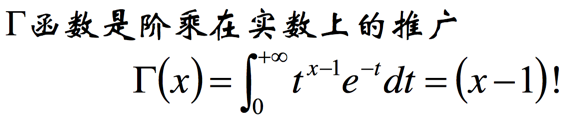
Beta分布

Beta分布的期望

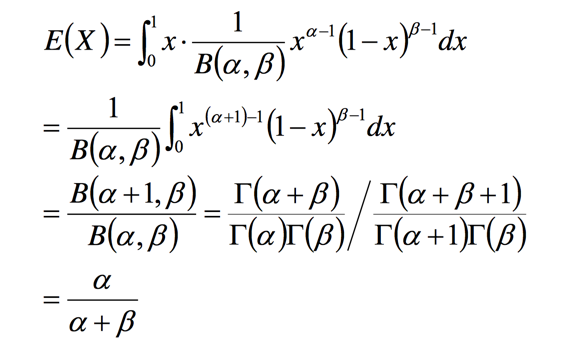
此处举个例子 alpha = beta = 2，则f(x)=(x-x^2)/6

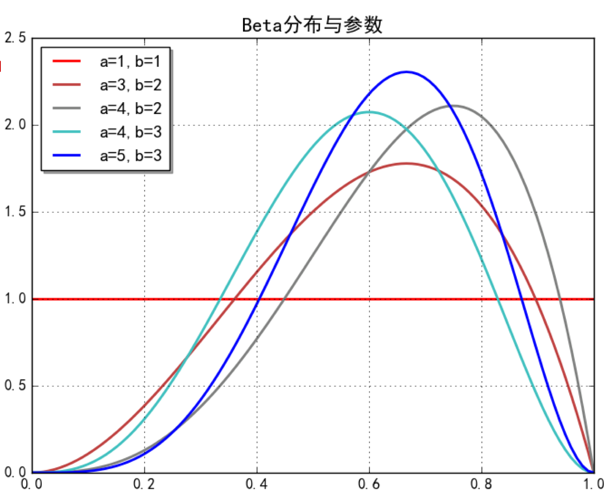
此处需要有的一个认识是：alpha 和 beta 越大，则整个曲线越高窄。

二项分布
投硬币实验，投掷n次，其中k次朝上，n-k次朝下，假定朝上的概率为theta，则此时概率为：

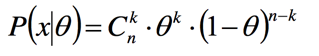
现在我们在观测到N次投掷的结果后，可以更新朝上的概率theata：

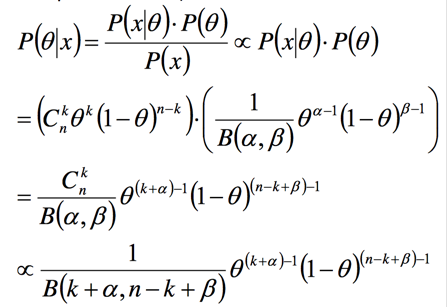
从上面的公式我们可以看到参数的先验概率和参数的后验概率都是beta分布。
解释

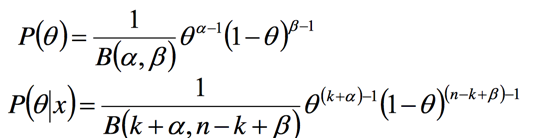
此处我们可以看到先验概率的含义是：正面朝上的概率，此处概率由参数 alpha 和 beta 决定，就是这个概率本身也是一个分布，我们能够知道这个正面朝上概率的期望是：

当我们观察到实验数据后，此时正面朝上的概率期望是：
$\frac{k+\alpha}{n+\alpha+\beta}$

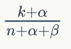
此处我们将 alpha 和 beta 看做是在没有任何假设的情况下，我们对朝上和朝下的一个先验计数。

多项分布

Dirichlet分布

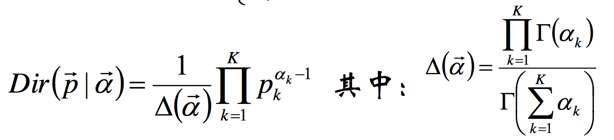
数学期望

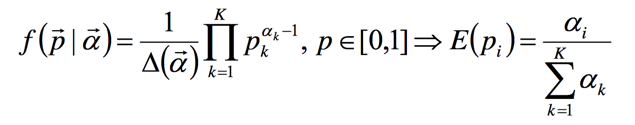
概率密度函数的数学期望是一个真实的概率。
对称 Dirichlet 分布
针对不同 alpha 时，曲线的形状，根据之前在看 beta 分布时候的一个直觉，应该是 alpha 值越大，曲线越陡峭。

我们假设我们有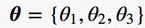，并且满足相加为1，则我们可以画出图：

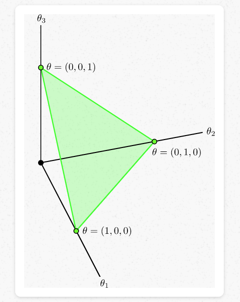
此三角形平面是所有可能的取值，而 Dirichlet 分布则是用来描述这个平面上哪些区域取值可能高，即概率密度。

下面是取不同的 alpha 值时候概率图，越深表示越大：

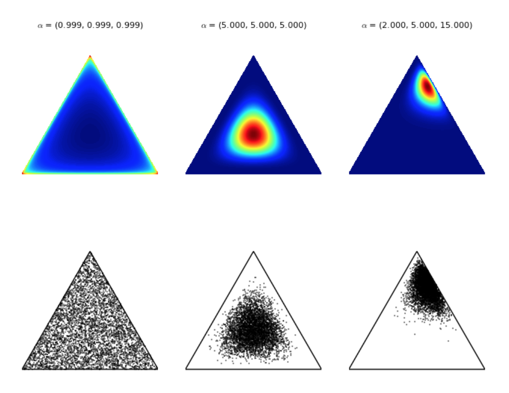
所以我们可以知道 alpha > 1的时候，越是趋向于取均值，而 alpha < 1 的时候，趋向于取角上的值。

Visualizing Dirichlet Distributions with Matplotlib

我们可以通过伪计数的方式来理解下： 当 alpha 的值越大，越表明其先验概率大。

共轭
多项分布 Multinomial distribution

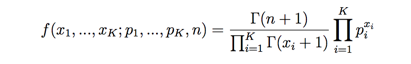
狄利克雷分布 Dirichlet distribution

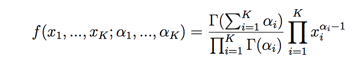
现在我们假设有：

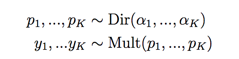
则后验也服从Dir分布

更具体推导可以看dirichlet-conjugate-prior