贝叶斯统计：初学指南

贝叶斯

什么是Bayesian Statistics？

Bayesian statistics is a particular approach to applying probability to statistical problems。

在statistical inference上，主要有两派：频率学派和贝叶斯学派。

Frequentist statistics tries to eliminate uncertainty by providing estimates. Bayesian statistics tries to preserve and refine uncertainty by adjusting individual beliefs in light of new evidence.

贝叶斯推理的目标？

produce quantitative trading strategies based on Bayesian models.

在使用贝叶斯理论过程中，我们最基本的公式如下：

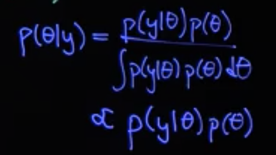
为了方便的计算后验概率，我们会采用共轭先验的方法来简化后验的计算。
举个简单例子，假设我们投掷一枚硬币，我们刚开始认为正面朝上的概率是服从一个Beta分布的，Beta分布能产生一个0-1之间的随机数。

我们刚开始假设α = β = 1，则Beta分布退化为一个均匀分布，接着我们不断的投掷硬币，记录好每次投掷的结果，然后根据结果再来计算此时正面朝上的概率。
此时我们可以计算出n次中k次朝上的概率值为：

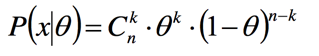
我们再来计算后验概率：

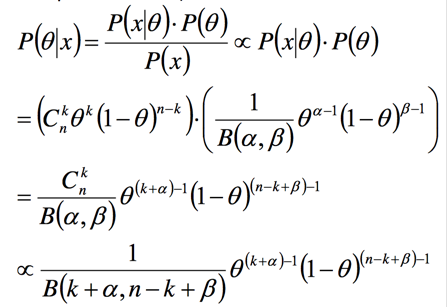
可以看到后验概率也是Beta分布，我们通过假设先验概率为Beta分布，能非常方便的计算出后验概率。

下面是一段实验代码：

产生的图如下：

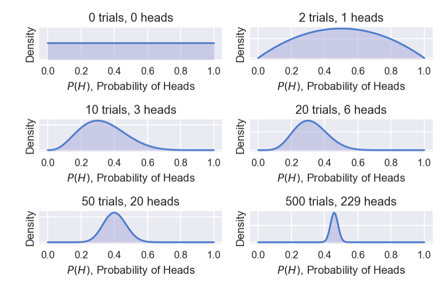
随着实验结果的增加，我们越来越确信正面朝上概率为0.5。

以上是一个简单的后验问题，如果遇到一些复杂的后验概率，我们就要使用mcmc来做了.

MCMC is a means of computing the posterior distribution when conjugate priors are not applicable.

我们再来看后验的计算公式：

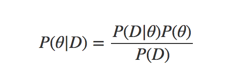
此处要想计算出解析解，就必须知道evidence P(D)，其计算公式如下：

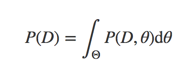
这里的问题就是我们一般很难求联合概率的积分，所以我们要通过数值逼近的方法来求P(D)。其中有一大类算法是：Markov Chain Monte Carlo Algorithms，有 Metropolis Algorithm, Metropolis-Hastings, the Gibbs Sampler, Hamiltonian MCMC and the No-U-Turn Sampler (NUTS).

注：此处为什么积分困难，可以看为什么要使用 MCMC 方法？

MCMC 的应用是和 "维数灾难" 有关的。考虑一个 R 上的分布，如果我们要计算它的数学期望，采用题主所描述的 "等距计算"，那么取 100 个点大致可以保证精度。然而考虑一个 R^50 的分布，这时候要采用 "等距计算" 就要在每个维度上取 100 个点，这样一来就要取 10^100 个点。作为对比，已知宇宙的基本粒子大约有 10^87 个。如果仔细观察 "等距计算" 的结果，就会发现绝大多数点算出的概率都很小，而少部分点的概率非常大。而如果我们忽略大多数概率小的点，只计算概率大的那小部分点，对最后数学期望的结果影响非常小。这是 MCMC 思路的直观部分。MCMC 应用的概率模型，其参数维数往往巨大，但每个参数的支撑集非常小。比如一些 NLP 问题的参数只取 {0,1}，但维数往往达到几千甚至上万左右，这正说明了 MCMC 更适用这些问题。

下面介绍第一个算法：Metropolis 算法。

先介绍 mcmc 算法的一般套路：

1. 先在参数空间$\theta$中选择一个$\theta_{current}$
2. 在参数空间中提议一个新的位置$\theta_{new}$
3. 根据先验信息和观测数据决定接收或者拒绝$\theta_{new}$
4. 如果接收跳跃，则跳转到新的位置，并且返回到step1
5. 如果拒绝，则保持当前位置并返回到step1
6. 连续采用一系列点，最后返回接受的点集合

不同的mcmc算法的区别就在于：

how you jump as well as how you decide whether to jump.

Metropolis 使用正态分布来进行跳跃，正态分布的μ为当前位置的$\theta_{current}$，然后σ是需要决定的。σ 是 Metropolis 算法的参数，不同的 σ 值决定了算法的收敛速度。如果 σ 值大，意味着 proposal width 宽，能够跳的更远，并且搜索更多的后验参数空间，但是容易跳过高概率的地方，但是过小的σ 值，又会使得proposal width过小，导致收敛过慢。

一旦新的位置被提议出来，下一步就是要决定是否要跳转了，我们计算两个位置的概率比值：

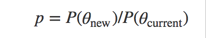
然后我们从[0,1]的均匀分布中采出一个值，如果在[0,p]之间就接受，否则拒绝。

下面我们来对上面过程举个例子来说明。
假设我们有一组观测数据，来自一个正态分布，我们假设参数μ的先验分布也是一个正态分布，公式描述如下：

μ∼Normal(0,1) # 参数先验概率

x|μ∼Normal(x;μ,1) # 似然

我们通过代码采样如下:


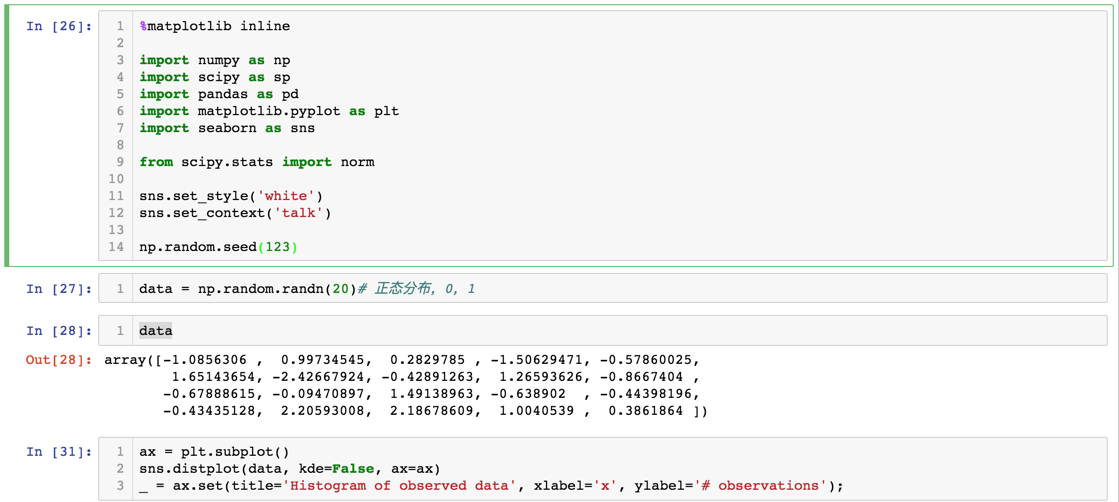
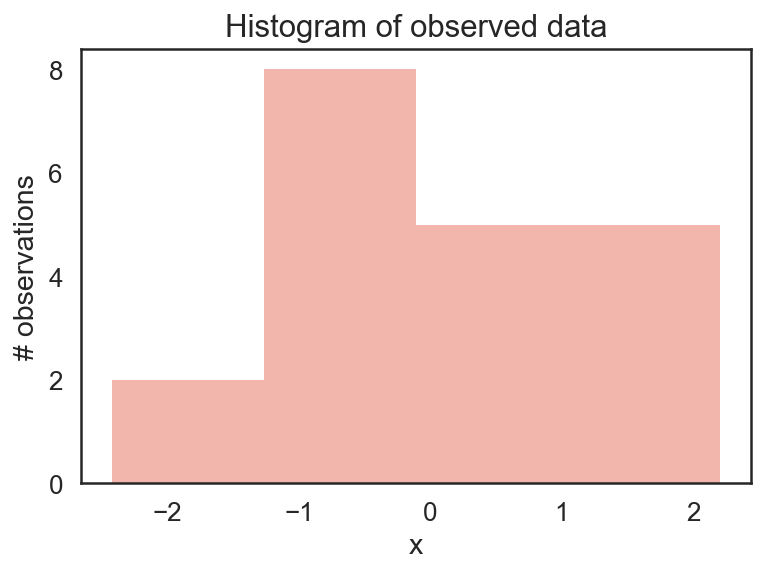
对于这个问题，我们为了对比mcmc的结果，该后验概率我们是可以直接计算出来的，具体的数学推导见:note

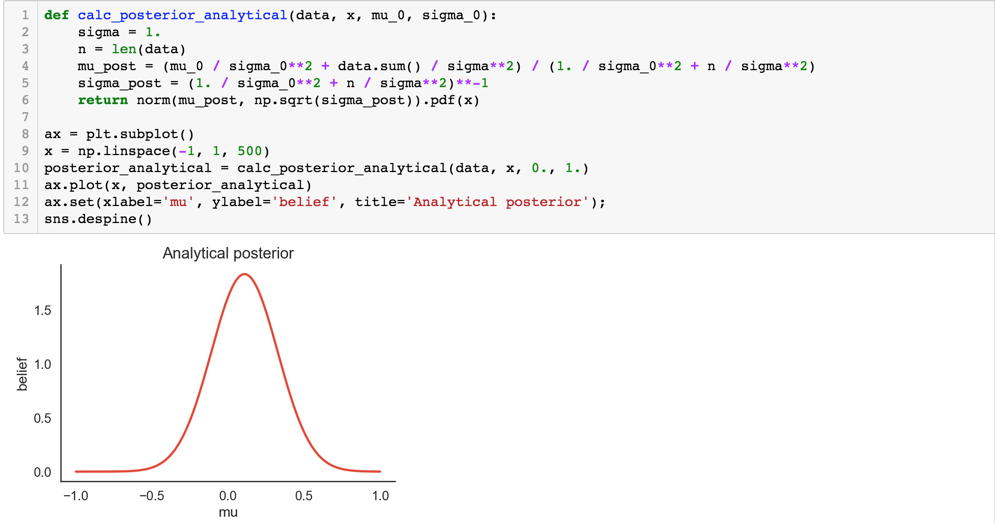
我们对照上面说的 mcmc 算法的一般套路，先采样：

挑选出新的值后，我们下一步就是要去衡量新的参数好不好，怎么定义好不好呢？就是看新的参数是否能更好的解释数据。
怎么去定义更好的解释数据呢？
可以用下面的公式

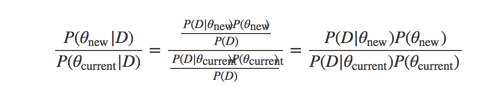
解释起来就是基于当前观测数据，哪个参数概率更大。
下面就是决定是否要接收新参数了：

然后不断重复上面的过程，我们就有了一系列的$\theta$了。
完整的代码可以见mcmc。

总结

本文主要介绍mcmc，其解决了当后验概率太复杂时候，用采用的方法去近似后验分布，本文介绍了最简单的 Metropolis 算法，后面会继续学习其他算法，欢迎关注。

参考

Markov Chain Monte Carlo for Bayesian Inference - The Metropolis Algorithm
MCMC sampling for dummies
Bayesian Inference with PyMC3 - Part 1

你的鼓励是我继续写下去的动力，期待我们共同进步。