群和旋转

Barfoot

---

群

合成法则

所谓合成发着，即一个二元运算，或者说有一个两个变量的映射或者函数:

$$S \times S \rightarrow S$$
此处$S \times S$表示集合的积集，他的元素是S中的元素对
合成法则作用在元素$a$,$b$上所得到的元素通常用类似乘法或者加法的记号表示：
$$p = ab, a \times b, a \circ b, a+ b$$

元素p可以叫做$a$, $b$的和或者积，这取决于符号是加还是乘。大多数情况采用乘法，记为$ab$
若用乘法作为记号
结合律为： $(ab)c = a(bc)$
交换律为：$ab = ba$
值得注意的是，结合律比交换律更为基础，大量运算满足结合律而不满足交换律，一般满足交换律的群叫做阿贝尔群。
一般矩阵乘法和函数的复合都满足结合律，不满足交换律

---

群和子群

定义

满足下列性质的合成法则的集合G称为群：

• 结合律： $(ab)c = a(bc)$，对G中任意$a,b,c$成立
• G中有单位元$1$,即$1a = a1 = a$
• G中任意元素$a$有逆，即存在$b$，使得$ab = ba = 1$（注意左逆右逆都存在才可逆）

两个特殊的群

1. $n \times n$一般线性群是由所有$n\times n$可逆矩阵构成的群，记为：
   

   $$GL_n = \left \{ n \times n 可逆矩阵A \right \}$$

2. 指标集合$\left \{ 1, 2, \ ... \ , n \right \}$的置换群成为对称群，记作$S_n$（n个元素的置换群中一共有n!个置换，所以对称群$S_n$是n!阶的有限群）

子群

若群G的子集合H成为群G的一个子群，那么H满足下列性质：
- 封闭性： 若$a \in H, b \in H$，则$ab \in H$
- H中有单位元$1$,即$1a = a1 = a$
- H中任意元素$a$有逆，即存在$b$，使得$ab = ba = 1$

两个特殊的子群

1. 模为1的复数的集合，是乘法群$\left (C, \times \right )$的子群，称为圆群
2. 所有行列式为1的$n \times n$实矩阵构成的一般线性群$GL_n$的子群，称为特殊线性群,记作$SL_n$

---

同态

同态定义

假设G和G'为两个群，若映射$\varphi: G \rightarrow G'$是一个同态，则对G中任意元素$a,b$有:

$$\varphi(ab) = \varphi(a)\varphi(b)$$
直观上，一个同态就是与两个群中合成法则相容的映射
值得注意的是，如果等号左边为加法群，等号右边为乘法群，一般将同态条件记为:
$$\varphi(a+b) = \varphi(a)\varphi(b)$$
例如对于映射：$exp: \left (R, + \right ) \rightarrow \left( R, \times \right )$定义为:$x \leadsto e^x$,显然有$e^{a + b} = e^a e^b$

一些命题和定义

命题:若$\varphi: G \rightarrow G'$是群同态，则
1. 若$a_1, a_2,\ ... \ , a_k \in G$，则$\varphi(a_1\cdots a_k) = \varphi(a_1)\cdots \varphi(a_k)$
2. $\varphi(1_G)=1_{G'}$
3. $\varphi(a^{-1}) = \varphi(a)^{-1}$

定义：同态$\varphi:G\rightarrow G'$的像记作$im \varphi$或者$\varphi(G)$，它代表下面定义的集合:

$$im\varphi = \left \{ x \in G' | x = \varphi(a), a \in G \right \}$$

定义: 同态$\varphi$的核记为:$ker\varphi$，是指G中所有映射到G'恒等元的那些集合的元素的集合，即:

$$ker\varphi = \left \{ a \in G | \varphi(a) = 1 \right \}$$

值得注意的是，$im\varphi$是G'的子群，$ker\varphi$是G的子群

定义： 如果对于群G的子群N中任意元素$a$和G中任意元素$g$，$gag^{-1} \in N$，称N是G的正规子群

同构

定义： 如果$\varphi: G\rightarrow G'$是同构，那么$\varphi$是双射，且满足：$\forall a,b \in G$,有

$$\varphi(ab) = \varphi(a)\varphi(b)$$
同时，如果存在从G到G'的同构映射$\varphi$，那么我们称G和G'是同构的，记作:$G \approx G'$
值得注意的是，存在群G到自身的同构$\varphi$，这样的同构我们称为自同构，显然恒等映射是一个自同构，当然也存在其它的自同构，其中有一种重要的自同构是共轭：
令$g \in G$，由$g$得到的共轭是$G$到自身的映射，定义为：$\varphi(x) = gxg^{-1}$，此时元素$gxg^{-1}$成为x关于$g$的共轭
若$\exists g \in G$,使得,G中的$x, x'$满足$x' = gxg^{-1}$，我们称$x,x'$是共轭的

同胚

定义： 两个拓扑空间$\left \{ X,T_X \right \}$ 和 $\left \{Y,T_Y \right \}$ 之间的函数$f : X \rightarrow Y$ 称为同胚，如果它具有下列性质：
1. f是双射（单射和满射）
2. f是连续的
3. 反函数f−1也是连续的（f是开映射）

同胚是拓扑空间范畴中的同构。大致地说，拓扑空间是一个几何物体，同胚就是把物体连续延展和弯曲，使其成为一个新的物体。正方形和圆是同胚的，但球面和环面就不是。

商群

陪集

如果$H$是群$G$的子群，且$a \in G$，那么子集

$$aH = \left \{ ah | h \in H \right \}$$
称为左陪集，其中子群H是一个特殊的左陪集，因为H = 1H
实际上G中H的陪集类似于同余关系，实际上群G的子群H的左陪集将群G划分成了等价类

类似的可以有右陪集

$$Ha = \left \{ ha | h \in H \right \}$$
实际上这个是(右同余)的等价类，他们也构成了一个划分
可以发现，实际上正规子群的每一个左陪集都是右陪集

商群

我们在群G的正规子群N的陪集上定义合成法则，这个运算发证使得正规子群的陪集称为一个群，这个群称为商群
由于正规子群的每一个左陪集都是右陪集，所以正规子群的陪集通常用$G/N$表示，一般地我们用$G/N$表示正规子群N在G中的陪集的集合，这个集合记为$\bar{G}$

定理
令N是G的正规子群，$\bar{G}$为N在G中陪集的集合，那么存在$\bar{G}$上的一个合成法则使其称为一个群，使得定义为$\pi(a) = \bar{a}$的映射$\pi: G \rightarrow \bar{G}$是一个核为N的满同态
第一同构定理
设$\varphi: G\rightarrow G'$是一个满群同态，核$N = ker\varphi$，则商群$\bar{G} = G/ N$与像$G'$同构

---

线性群

首先定义一些线性群：

1. $n \times n$一般线性群是由所有$n\times n$可逆矩阵构成的群，记为：
   $$GL_n = \left \{ n \times n 可逆矩阵A \right \}$$
2. 实特殊线性群$SL_n$:
   $$SL_n = \left \{ P \in GL_n(R) | detP = 1 \right \}$$
3. 正交群$O_n$:
   $$O_n = \left \{ P \in GL_n(R) | P^tP = I \right \}$$
4. 酉群$U_n$:
   $$U_n = \left \{ P \in GL_n(C) | P^HP = I \right \}$$
5. 特殊正交群$SO_n$:
   $$SO_n = \left \{ P \in O_n | detP = 1 \right \}$$

---

然后说明我们熟悉一些线性群的图形，例如单位圆

$$x_0^2 + x_1^2 = 1$$
有几个群的体现，他们都是同构的。记$\left ( x_0, x_1 \right ) = \left ( \cos\theta, \sin \theta \right )$,即把圆周与角度的加法群等同起来，或者通过$e^{i\theta}$,把它看成复平面的单位圆，他就变成了乘法群($1\times 1$酉矩阵的群)：
$$U_1 = \left \{ p \in \{ C,+ \} | \bar{p}p = 1 \right \}$$

单位圆也可以通过映射

$$\left ( \cos\theta, \sin\theta \right ) \leadsto \left [ \begin{array} 0 \cos \theta & -\sin\theta \\ \sin \theta &\ \ \ \cos\theta \end{array} \right ]$$
嵌入到$R^{2 \times 2}$中，他与特殊正交群$SO_2$（平面旋转群）同构，这些本质上都是同一个群的三种不同的描述，即圆周群

---

球面

与$R^3$中单位球面类似，定义轨迹

$$\left \{ x_0^2 + x_1^2 + \cdots + x_n^2 = 1 \right \}$$
为在$R^{n+1}$中的n维单位球面，简称n-球面,记为$S^n$，因此，$R^3$中的单位球面是2-球面，$R^2$中的圆周为1-球面
在$\left (x_0, x_1, x_2 \right )$-空间$R^3$中，我们把$x_0$看作竖直轴，球面的北极为$p = (1, 0, 0)$
同时，将$\left \{ x_0 = 0\right \}$的轨迹与称为V的平面等同起来，若把V中坐标记为$v_1, v_2$，那么V中的点$(v_1, v_2)$对应于$R^3$中的$(0, v_1, v_2)$
定义球极平面射影$\pi: S^2 \rightarrow V$如图所示

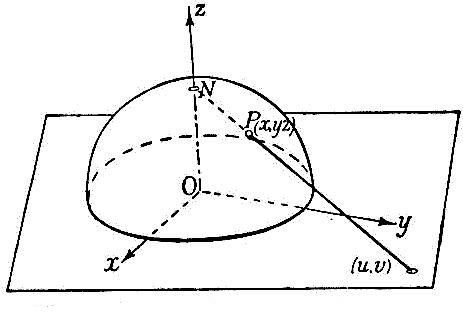
拓扑学上构造球面的方法是将一个球面作为平面V和北极这个单点的并
另一方面，由于北极把北半球双射到单位圆盘外，而南极的球极平面双射到单位圆盘内，二两个半球都和单位圆盘一一映射，所以这提供了第二种构造球的方法，即将它看成两个单位圆盘的并，这两个圆盘边缘粘在一起，然后像吹气球一样，吹大之后就可以成为一个真正的球。
我们感兴趣的是3-球面$S^3$(它总是和R^3可以一一映射)，实际上只需要构造为3-空间V和某个单点的并，或者在$R^3$中两个单位球$\left \{ v_1^2 + v_2^2 + v_3^2 \leq 1 \right\}$的并。

3-球面的经纬度

2-球面$\left \{ x_0^2 + x_1 ^2 + x_2^2 = 1 \right \}$上的常纬度曲线是水平圆周$x_0 = c$，而常经度曲线是通过极点的竖直大圆，经度曲线可以描述为2-球面和$R^3$中包含点$\left \{1, 0, 0 \right \}$的2维子空间的交集
3-球面和2-球面类似，我们取“水平”的曲面，即$x_0$为常数的曲面，我们称这个轨迹为纬，他们是由

$$x_0 = c, \ \ x_1^2 + x_2^2 + x_3^2 = (1 - c^2)$$
嵌入$R^4$的2-球面，当$x_0=0$时，这个特殊的纬成为赤道，记为$E$
作为经度曲线的类似，我们取通过北极$\left \{ 1, 0 ,0 ,0 \right \}$的大圆，他们是由3-球面与$R^4$的包含极点的2维子空间W的交集，交集$L=W \cap S^3$是W里的单位圆，我们称L为经。如果选取空间W的标准正交基$\left (p, v \right )$,则第一向量是北极，经由参数方程
$$L:l(\theta) = \cos\theta p + \sin\theta v$$

特殊酉群$SU_2$

$SU_2$的元素是形如

$$p = \left [ \begin{array} 0 \ \ a & b \\ -\bar{b}& \bar{a}\end{array} \right ] , \qquad 其中\bar{a}a + \bar{b}b = 1$$
的$2\times 2$的复矩阵，对于这个矩阵，$a = x_0 + x_1i, b = x_2 + x_3i$定义了$SU_2$与$R^4$中3-球面$\left \{ x_0^2 + x_1^2 + x_2^2 + x_3^2 = 1\right \}$的一一映射
$$p = \left [ \begin{array} 0\ \ x_0 + x_1i & x_2 + x_3i \\ -x_2+x_3i & x_0 -x_1i \end{array} \right ] \leftrightarrow \left (x_0,x_1,x_2,x_3 \right )$$
对于球面上北极$e_0 = (1, 0, 0,0)$显然对应与单位矩阵$I$，其他标准基向量是定义四元数群的矩阵，如下
$$\vec{i} = \left [ \begin{array} 0 i & \ \ 0 \\ 0 & -i \end{array} \right ] \quad \vec{j} = \left [ \begin{array} 0 \ \ 0 & 1 \\ -1 & 0 \end{array} \right ] \quad \vec{k} = \left [ \begin{array} 0 0 & i \\ i & 0 \end{array} \right ] \qquad \leftrightarrow \qquad e_1, e_2,e_3$$

这些矩阵满足诸如$ij=k$这样的关系，我们把具有基$\left (I, \vec{i}, \vec{j}, \vec{k} \right )$的实向量的空间叫做四元数空间，所以$SU_2$可以看成四元数代数里面单位向量的集合

实际上，除了两种特殊矩阵$\pm I$以外，$P$的特征值是模为1的共轭复数，在$SU_2$中，纬是共轭类，对于区间$-1 < c < 1$中给定的c，纬有$SU_2$中使得traceP = 2c的矩阵$P$组成，剩下的共轭类为${I}和{-I}$，他们构成了$SU_2$的中心(因为总能找到矩阵$Q$，使得$Q^TPQ = \Lambda$,所以对于特征值相同的矩阵，是共轭的)，而当$x_0=0$时，显然有

$$A = \left [ \begin{array}0 \quad \ x_1i & x_2 + x_3i \\ -x_2 + x_3i & \quad -x_1i \end{array} \right ] = x_1\vec{i} + x_2\vec{j} + x_3 \vec{k}$$

这样的A，我们成为赤道$E$，它对应的矩阵的迹traceP=0，值得注意的是A是斜埃尔米特矩阵
实际上对于，迹为0的$2\times 2$斜埃尔米特矩阵构成的3维度实向量空间V是一个与I正交的空间，他有基$\left ( \vec{i}, \vec{j}, \vec{k} \right )$,E正好是这个空间中的2-球面

令W是$R^4$的包含极点$I$的2维子空间，且设L是W里单位向量的经，那么
1. L交赤道E于两个点，如果A是其中一个点，那么另一个点是-A，而且，(I,A)是W的标准正交基
2. L的元素可以写成$P_{\theta} = (\cos\theta)I+(\sin\theta)A$，其中A在E上
3. 除了$\pm I$以外，$SU_2$的每个元素都位于唯一的经上，元素$\pm I$位于每个经上
4. 经是$SU_2$的共轭子群

下面我们说明特殊酉群$SU_2$的元素$P$确定个共轭作用(记为$\gamma_P)$旋转这个球面，也就是说我们可以用特殊酉群$SU_2$描述3维旋转群$SO_3$

---

旋转群$SO_3$

旋转

定义: $R^3$的关于原点的旋转是一个具有如下性质的线性算子$\rho$:
1. $\rho$固定单位向量$u$，称为$\rho$的极点
2. $\rho$旋转与$u$正交的2维子空间W
我们也称恒等算子为一个旋转，尽管它的轴是不确定的，而非恒等旋转用对偶$\left ( u, \theta \right )$描述，称为自旋，由极点$u$和非零旋转角$\theta$组成，这样的旋转记为$\rho_{(u, \theta)}$

欧拉定理
$3 \times 3$旋转矩阵是行列式为1的正交矩阵，它是特殊正交群$SO_3$中的元素

定理的推论
1. 绕任意两个轴的旋转的合成是绕某个其他轴的一次旋转
2. 若$M \in SO_3$表示具有自旋$(u, \alpha)$的旋转$\rho_{(u, \alpha)}$，那么有
$\quad$ 1) $M$的迹为$1 + 2\cos\alpha$(可以考虑不同基矩阵的迹不变)
$\quad$ 2) 令$B \in SO_3$，且$u' = Bu$,那么M的共轭$M'= BMB^t$表示带有自旋$(u', \alpha)$的旋转$\rho_{(u', \alpha)}$ (考虑转轴是旋转矩阵的特征值1所对应的特征向量)

$SO_3$

1. 规则$P \leadsto \gamma_P$定义满同态$\gamma : SU_2 \rightarrow SO_3$，即自旋同态，它的核是$SU_2$的中心$\{ \pm I \}$
2. 设$P=\cos\theta I + \sin \theta A$，其中$0 < \theta < \pi$,且$A \in E$,那么$\gamma_P$为绕极点$A$将$E$旋转$2\theta$，所以$\gamma_P$由自旋$(A,2\theta)$表示

显然有前面的第一同构定理有$SO_3$同构于商群$SU_2/Z$，其元素为对极点的偶对，即Z的陪集$\left \{ \pm P \right \}$(这里有一个划分，得到两个等价类)，可以看出$\gamma$是二对一的，因此我们说$SU_2$是$SO_3$的双重覆盖(实际上自旋$(A, \alpha)$和$(-A, -\alpha)$表示同一个旋转，二对一的一个映射)