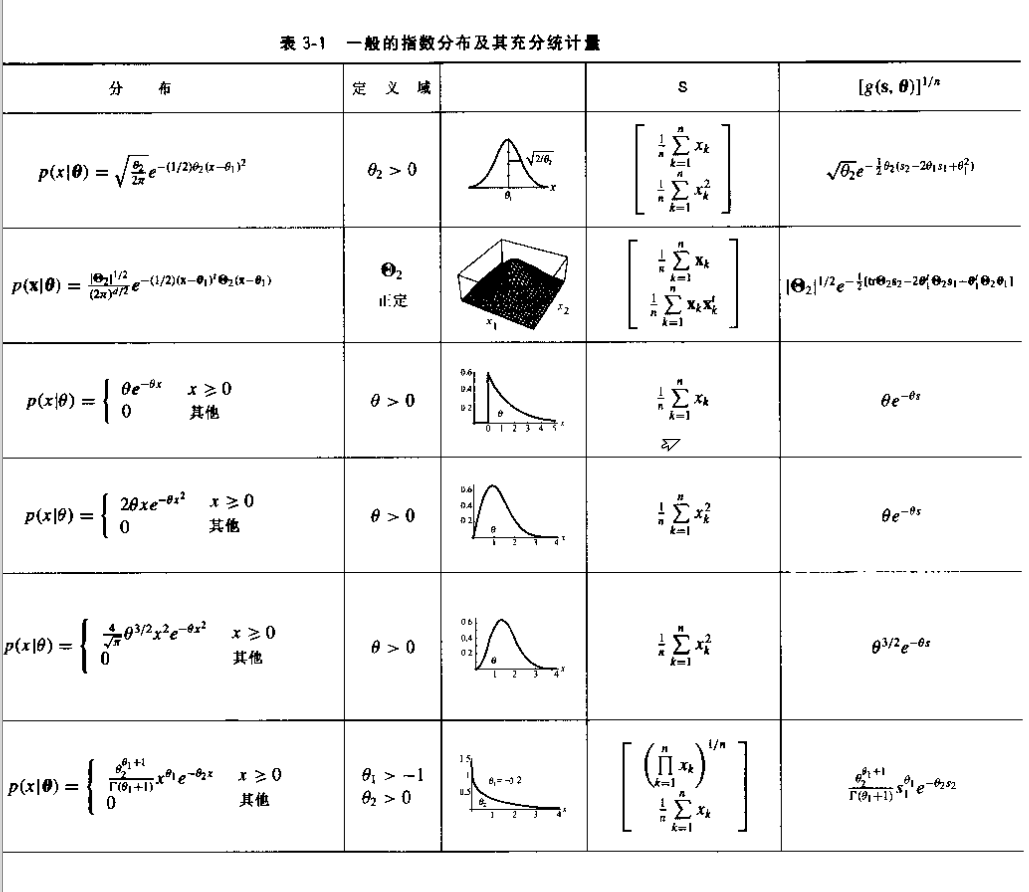
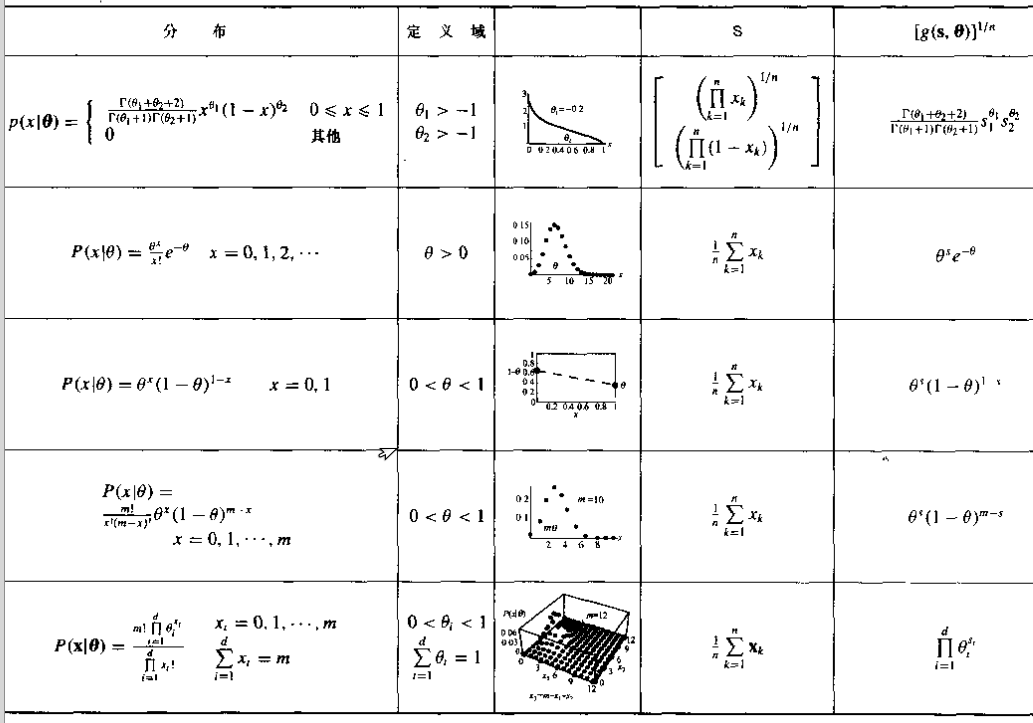
充分统计量

模式分类

@author lancelot-vim

定义

我们把任何关于样本集$D$的函数都称为一个统计量，一个充分统计量就是一个关于样本集$D$的函数$s$（允许是向量形式的函数)，其中包含了能有助于估计某种参数$\theta$的全部相关信息，就是说我们希望充分统计量的定义能够有这样的约束条件：$p(\theta|s,D)=p(\theta|s)$

举个例子说：对于高斯分布，期望和协方差矩阵就是它的充分统计量，因为如果这两个参数已知，就可以唯一确定一个高斯分布，而对于高斯分布的其他统计量，例如振幅，高阶矩等在这种时候都是多余的。

因式分解定理

充分统计量的最基本定义是因式分解定理，即如果$S$是$\theta$的充分统计量，那么$p(D|\theta)$可以写成一个只依赖于$s和\theta$的函数和一个只与样本有关的函数的乘积，用数学的语言描述如下：

$s是\theta$的充分统计量，当且仅当$P(D|\theta)=g(s,\theta)h(D)$

充分统计量和指数族

假如$s是\theta$的充分统计量，将$P(D|\theta)=g(s,\theta)h(D)$代入贝叶斯一般理论公式$p(\theta|D)=\frac{p(D|\theta)p(\theta)}{\int p(D|\theta)p(\theta)d\theta}$可得：$p(\theta|D)=\frac{g(s,\theta)p(\theta)}{\int g(s,\theta)p(\theta)d\theta}$，假如我们对$\theta$很不确定，那么可以选择一个近似与均匀分布的$p(\theta)$，在这种情况下，实际上$p(D|\theta)$就几乎等于核函数$\bar{g}(s,\theta) = \frac{g(s,\theta)}{\int g(s,\theta)d\theta}$

一个正态分布的示例

对于一个协方差已知，期望未知的正态分布，假设$p(\vec{x}|\vec{\theta}) \sim N(\vec{\theta}, \Sigma)$有：
$p(D|\vec{\theta}) = \Pi_{k = 1}^{n}\frac{1}{(2\pi)^{\frac{d}{2}}|\Sigma|^{\frac{1}{2}}}\exp[-\frac{1}{2}(\vec{x}_k - \vec{\theta})^T\Sigma^{-1}(\vec{x}_k - \vec{\theta})] \\ \qquad \quad = \exp[\frac{n}{2}\vec{\theta}^T\Sigma^{-1}\vec{\theta} + \vec{\theta}^T\Sigma^{-1}\vec{x}_k(\sum_{k=1}^n\vec{x}_k)] \times \frac{1}{(2\pi)^\frac{nd}{2}|\Sigma|^\frac{n}{2}} \exp[-\frac{1}{2}\sum_{k = 1}^{n}\vec{x}_k^{T}\Sigma^{-1}\vec{x}_k] \\ \quad \quad \quad = g(\hat{\vec{u}}_n, \vec{\theta}) \times h(D)$

$\quad$ 其中$\hat{\vec{u}}_n = \frac{1}{n}\sum_{k = 1}^{n}\vec{x}_k$

根据核函数公式：$\bar{g}(s,\theta) = \frac{g(s,\theta)}{\int g(s,\theta)d\theta}$，可得：$\bar{g}(\hat{\vec{u}}_n, \vec{\theta}) = \frac{1}{(2\pi)^{\frac{d}{2}}|\frac{1}{n}\Sigma|^{\frac{1}{2}}}\exp[-\frac{1}{2}(\vec{\theta} - \hat{\vec{u}}_n)^{T}(\frac{1}{n}\Sigma)^{-1}(\vec{\theta} - \hat{\vec{u}}_n)]$

指数族函数

对于可用$p(\vec{x},|\vec{\theta}) = \alpha(\vec{x}) \exp(a(\vec{\theta}) + b(\vec{\theta})^{T}c(\vec{x})$来表示的函数叫做指数族函数，其几乎包括了常用的所有分布，对于这种函数，如果它作为某个事件的概率密度，那么总能使用核函数方法来估计分布

• $\vec{s}= \frac{1}{n}\sum_{k = 1}^{n}c(\vec{x}_k)$
• $g(\vec{s},\vec{\theta})=\exp[na(\vec{\theta} + b(\theta)^T\vec{s}]$
• $h(D)=\Pi_{k = 1}^{n}\alpha(\vec{x}_k)$

下一篇：主成分分析和判别函数