贝叶斯判别与神经网络

模式分类

神经网络

我想凡是对机器学习有所了解的人，都不会对神经网络感到陌生(你可能不太清楚决策树或者随机森林是怎么工作的，但神经网络估计已经当做黑匣子使用了无数次)，尽管神经网络使用起来很简单，而且现有的很多框架(torch, tensorflow,matconvnet , caffe ...)对于神经网络的搭建给了一个很友好的方法，但是实际上神经网络本身却是有着比较深刻的概率意义。

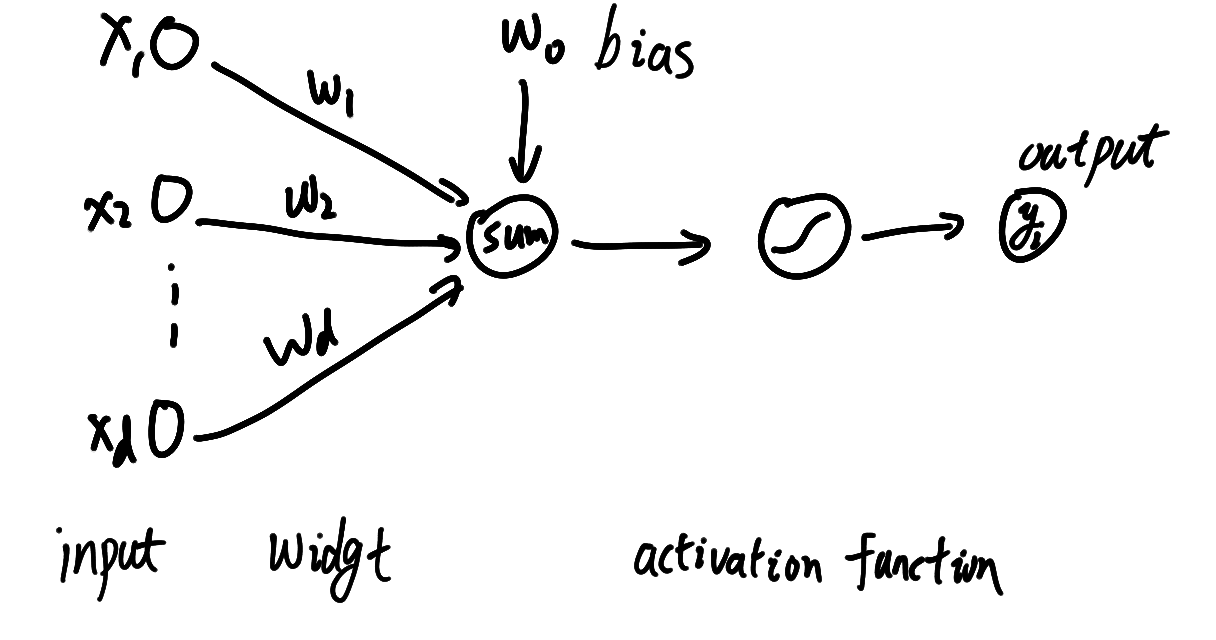
我想没有什么图片比上面那个图片更能说明神经网络结构的(虽然它只是一个简单的感知器),但是实际上神经网络总是这些个感知器堆积起来的一个复杂的感知器结构，如下图

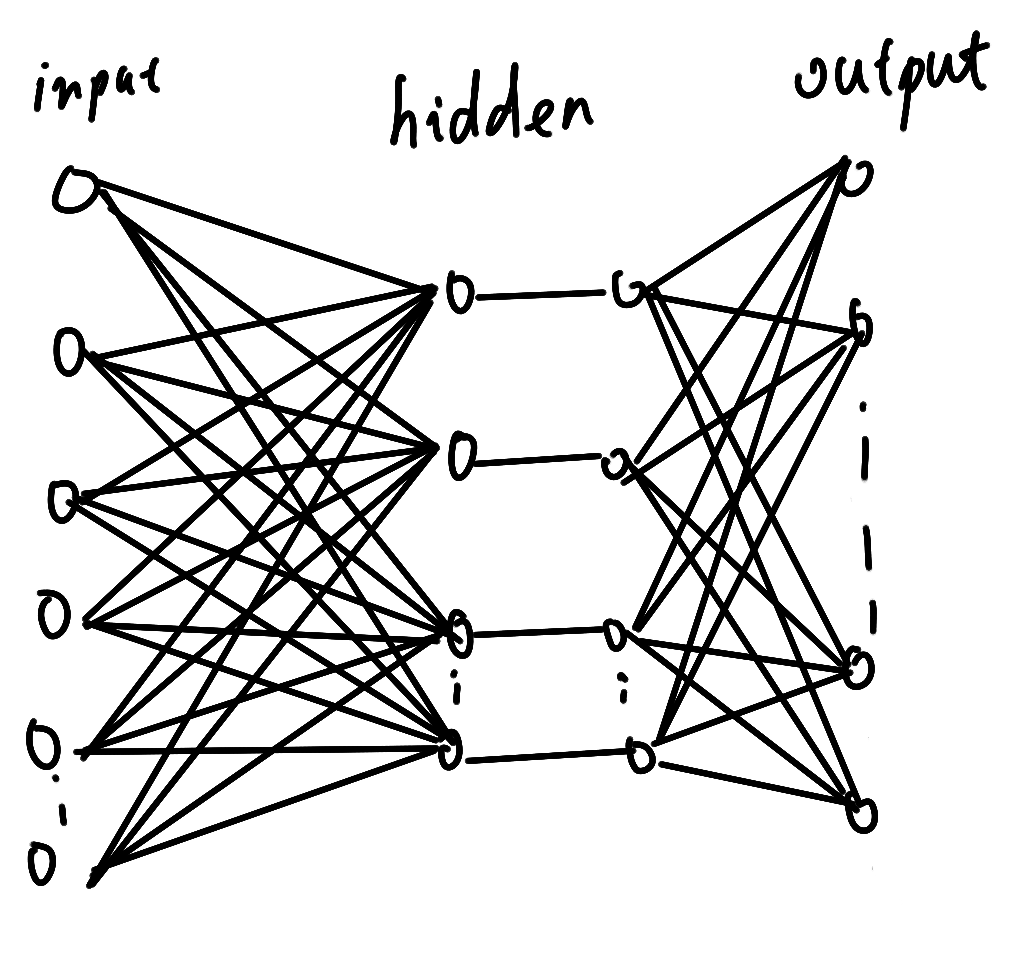
对于个判别函数(输出层)，都有一个感知器与之对应，最后得到这个输入在某各类的后验概率值，对应于最大的那个概率，往往我们就认为是那个类型。
简单地写成公式，假设$f(\cdot)$为激活函数(activation function)

$$y_k = f(\sum\limits_{j}w_{kj}x_j + w_0)$$

或者写成(假如y又连接了一个判别函数g)

$$g_k = g(\sum\limits_{j}w_{kj}f(\sum\limits_{i}w_{ji}x_i + w_{j0}) + w_{k0})$$

但无论是怎样的结构，它们都是简单的感知器的累加而已，那么很自然而然地会想到，是不是对于每一种判决都能够用这样的简单的感知器累加就能实现呢？
实际上很早之前Kolmogorov就已经告诉我们：

任何从输入到输出的连续映射函数，都可以用一个三层非线性网络实现，只要能给出足够数量的隐藏单元，并且给出恰当的非线性函数(激活函数)和权值

但实际上，这个定理并没有太多的实用价值，对于模式识别或者人工智能来说，选取激活函数和设置隐藏层数量，总是我们需要实用的核心问题，但是这个定理却给了我们一种保证，即任何后验概率衍生而来的判别函数，都能用这样的网络结构进行拟合

bp算法

关于bp算法的内容，我不想在这里多写，一方面在网上很多博客，或者教科书上总能找到相应的内容，另一方面，所有的深度学习框架都已经将这个算法封装而且优化地很好，(如果没有，扔掉它）,况且，我觉得这个东西对于整个神经网络的理解来说，也是不那么重要的，它只是使用迭代法把误差最小化而已，而这个过程正好后面层算处的$\delta$可以给前面层使用，因此梯度从后面向前面更新，直到误差很小，这个算法虽然如此经典，以至于现在深度学习研究人员都对此乐此不疲，但是他对整个网络的理解并没有产生那么大的作用，因此我就这一段，献给bp算法以及发明这个算法的科学家。

隐藏层的内部表示

回到网络进行分析，线性代数告诉我们，有限次线性变换后的结果还是一个线性变换，如果网络中仅仅只有一些"内积"，那是无法拟合一个线性不可分的情况的，但实际上我们在网络中加入了激活函数，这就使得网络中间层是一些非线性单元的线性组合，实际上我们是通过这种线性组合，对一个很复杂的函数进行近似，或者，假如把隐藏层处理过程看成寻找"特征组合"的过程，那么实际上，每个单元就是一个被激活的特征，这个特征正好是输入层经过某种非线性变换(或者线性变换)，变换到特征空间的其中一个特征基底，然后再将这些特征进行线性组合，送给判别函数计算后验概率，输出层的结果
其实我们可以证明，如果采用均方根误差进行反向传播训练，那么多层神经网络最后你和了一个贝叶斯判别函数的最小二乘判别