lsd-slam源码解读第三篇:算法解析

lsd-slam

我希望朋友们看着篇博客的时候已经看过我写的第二篇:lsd-slam源码解读第二篇:DataStructures
与此同时对代码已经有一定的了解,如果有朋友还未下载到源码，请看我的第一篇:http://blog.csdn.net/lancelot_vim/article/details/51706832

当你对Frame有一定的了解后，自然希望知道这个算法是如何构建的(所谓程序=数据结构+算法)
需要先了解整个slam是如何运作的

我直接把论文中的图片截了过来，实际上整个过程分为三大模块，第一个模块是Tracking,第二个模块是Depth Map Estimation, 第三个模块是Map Optimization，这三个过程分别位于论文的3.3，3.4和3下的其他部分(实际上Optimization可以说是整个算法的核心部分)

Tracking

回想之前写过的数据结构Frame，里面包含了图像，深度和深度方差，即

式中下标i表示关键帧的id,I表示从图像向一个实数的映射，D表示深度图到正实数的映射，V表示深度的方差到正实数的映射(注意这里的深度都是逆深度，简单称呼成深度)

当一个新的图像(或者说新的观测)输入时，认为它与关键帧之间有个se(3)的变换关系，这个变换关系我们需要根据关键帧和当前图像的数据优化得到，优化方程为

这似乎看起来是比较抽象的几个方程，实际上可以简单地理解把r理解为图像误差，sigma理解为不确定度，w表示从图像向keyFrame的一个映射(先映射之后，发现可能对应点没有重合，出现误差),最后是误差的衡量边准，E是总的误差。
最后实际上我们就通过优化E，算出当前观测到的图像到关键帧的变换，从而得到当前的位置姿态信息

Depth Map Estimation

tracking成功之后，就进入深度估计过程，首先是判断，是不是新建关键帧，论文中如此写道：

If the camera moves too far away from the existing map, a new keyframe is created from the most recent tracked image.

就是说关键帧的创建是根据相机移动来判断的，如果相机移动了足够远，那么就重新创建一个关键帧，否则就refine当前的关键帧
事实上，这个过程有一整套很复杂的过程，在论文Semi-Dense Visual Odometry for a Monocular Camera中，且让我慢慢道来

深度估计主要有三个过程，分别是：
1. 用立体视觉方法来从先前的帧得到新的深度估计
2. 深度图帧与帧之间的传播
3. 部分规范化已知深度

基于立体视觉对深度的更新

首先，跟新深度我们需要选择参考帧，让我们的深度估计尽可能精确，但是与此用时，希望差异搜索范围和观测角度尽可能小(效率高)，这个算法中使用了一种自适应的方法:

We use the oldest frame the pixel was observed in, where the disparity search range and the observation angle do not exceed a certain threshold (see Fig. 4). If a disparity search is unsuccessful (i.e., no good match is found), the pixel's "age" is increased, such that subsequent disparity searches use newer frames where the pixel is likely to be still visible.

实际上就是搜索到最先看到这些像素的帧，一直到当前帧的前一帧作为参考帧，如果搜索失败，说明匹配很差，那么就增大像素的"年龄"，让它在新的能够看到这些像素的帧里面能够被搜索到

确定了搜索帧的范围之后，知道如何对每一帧进行操作。
其实方法很简单，对于每个像素（我估计是有效的像素），沿着极线方向搜索匹配，(不知道啥叫极线的朋友，可以看下我写的一篇翻译外国书的博客: 对极几何与基本矩阵)，论文上有讲到，如果深度估计是可用的，那么搜索范围限制到均值加减2倍方差的区间，如果不可用，那么所有的差异性都需要被搜索，并使用，最后使用SSD误差作匹配算法，我找到一篇博客，对视觉匹配误差有个比较完整的总结:基于灰度的模板匹配算法（一）：MAD、SAD、SSD、MSD、NCC、SSDA算法

说明了以上两点之后，我们需要说明深度的到底是如何计算的。
就实际上而言，我们需要考虑从两幅图片I0,I1以及他们相对的朝向kesi还有投影矩阵pi中得到一个最好的深度估计值，在得到这个估计值的同时，计算出它的可靠度，即
,

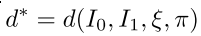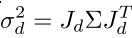
就实际运作而言，也是分为三大步：
1. 参考帧上极线的计算
2. 极线上得到最好的匹配位置
3. 通过匹配位置计算出最佳的深度

在这个三大步中，第一步需要得到几何差异误差，第二步需要得到图像差异误差，最后一步需要根据基线量化误差

几何误差 几何误差来源于相对朝向以及投影矩阵，假设极线L属于R2空间，可以用下面的表达式定义：

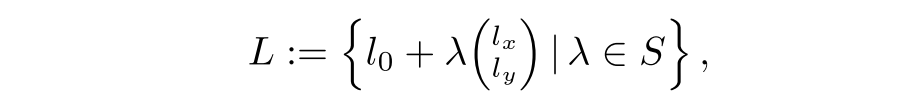
其中S是差异性区间，(lx,ly)^T是极线的单位化后的方向向量，l0表示一个对应无限深度的点。我们现在假设线单元上只有直线位置，l0受到高斯噪声，在实际应用中，我们需要极线尽可能短，旋转的影响尽可能小，使得这个估计尽可能好

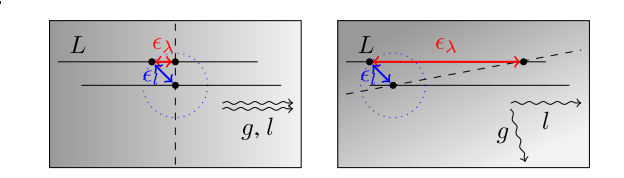
如图所示，虚线是图像的等值线，等值线上的两个点，是同样深度的点，L是极线，el极线的高斯误差，e(lambda)是几何误差，明显的是，如果L平行与梯度方向，实际上误差会比较小，如果几乎垂直了，误差会很大
因此论文上有这样一个"定义为"的公式:

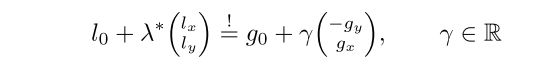
g0表示等值线上的某个点，g=(gx,gy)^T表示图像的梯度方向
将上面式子l0移项，然后两边同时点乘g,之后将分母移到等号右边可以得到最后的lanbda的优化表达式：

然后根据协方差传递的公式，最终可以得到：

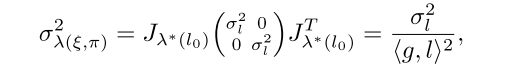
图像误差

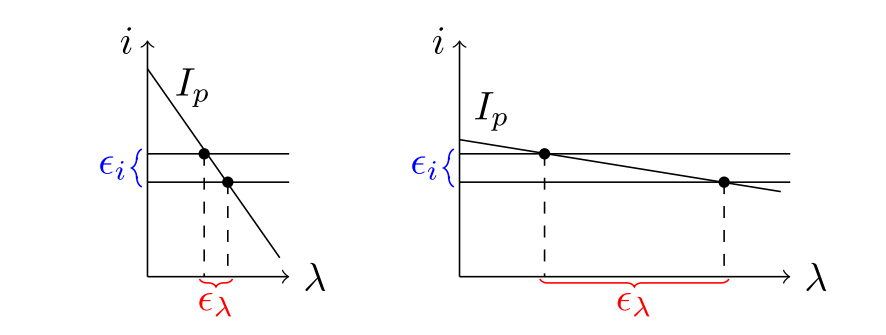
如图所示，如果梯度灰度梯度绝对值越大，对差异影响越小，反过来，如果绝对值越小，影响反而会很大，把这个公式化，我们实际上是要找到一个lambda,使得他们的差异最小，即

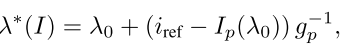
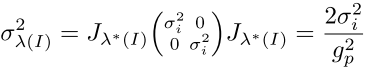
其中iref是参考的灰度，Ip(lambda)是当前图像在极限差异lambda，gp是梯度

直观理解
我试图说明这个想法，让这个理解起来比较直观，简单说，测量都是不精确的(如果你能有完全精确的测量方法，请告诉我，让我膜拜几十年)，因此我们希望的是能够在有扰动的情况下，让这个扰动对深度的影响足够小，也就是让$\lambda$变化足够小(深度预测总是和极线相关的)，因此我们试图寻找下降的最快的方向(即梯度方向)，或者让梯度足够大
可以发现，第一个方案就是寻找了梯度的方向，第二个方案是让梯度足够大

像素到深度的转换
如图所示，通常$\lambda$ 与d是成比例的，我们计算总的观测不确定度为：

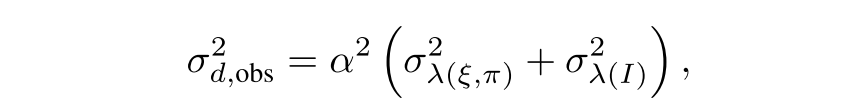
其中：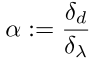

我会告诉你，这个实际上就是有限增量公式吗？

深度观测融合
之后，我们使用贝叶斯估计迭代算法(对于高斯分布实际上就是卡尔曼滤波)，来更新深度的估计，最终得到分布为：

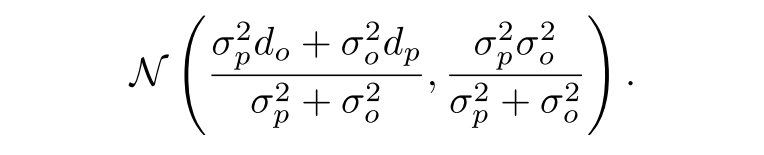
深度的前向传播

我们假设两帧之间相机的旋转很小，那么新的深度d1可以用下面公式计算

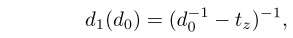
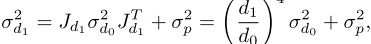
tz表示相机的平移，sigmod_p表示预测的不确定度

深度图的正则化

对于每一帧，我们使用一个正则迭代，把每个像素与其周边的加权深度作为改点的深度值，假如两个邻接深度之间的差值远大于2sigmod，他们便不做这个处理。但我们需要记住，处理之后，各自的方差不变

创建KeyFrame

现在回到主流程Tracking后的处理，如果是要创建关键帧，那么这个是很容易的，论文中是这么写的

Once a new frame is chosen to become a keyframe, its depth map is initialized by projecting points from the previous keyframe into it, followed by one iteration of spatial regularization and outlier removal as proposed in 9. Afterwards, the depth map is scaled to have a mean inverse depth of one - this scaling factor is directly incorporated into the sim(3) camera pose. Finally, it replaces the previous keyframe and is used for tracking subsequent new frames

就是说，新的关键帧需要之前的关键帧将点投影过来(投影方案已经在深度前传介绍过)，得到这一帧的有效点，深度通过sim(3)变换投影均值和缩放因子，最后用这个关键帧替换掉之前的关键帧

refine Depth Map

如果不创建关键帧，那么就用当前的观测对之前的深度进行修正，论文原文

A high number of very efficient small- baseline stereo comparisons is performed for image regions where the expected stereo accuracy is sufficiently large, as described in 9. The result is incorporated into the existing depth map, thereby refining it and potentially adding new pixels – this is done using the filtering approach proposed in 9.

实际上修正方法就是之前介绍的深度估计部分，使用贝叶斯后验概率算法，对深度进行修正，在这里也不再复述

Map Optimization

我估计看到这里，可能刚刚松了一口气，但是不得不说的是，我们进入了最后一个环节，全局地图优化
它的背景是这样的，单目slam由于它的绝对尺度信息是不能直接得到的(一只眼睛很难确定远近)，导致长距离运动之后，会产生巨大的尺度漂移。为了解决这个问题，我们需要对地图进行全局优化

首先我们需要插图关键帧到地图当中，要插入关键帧，自然需要知道什么时候需要插入，那么我们需要定义一个距离

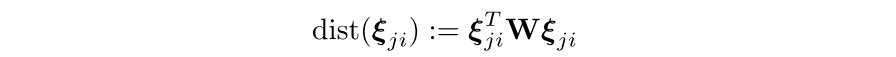
这里的W是一个对角阵，表示每个维度的权重，我们设定一个阈值，加入这个距离大于设定的阈值，那么就需要插入一帧，这个阈值实际上和当前场景有关，同时我们需要保证它足以满足小基线立体相机的要求

在插入帧的同时，我们还需要知道两帧之间是如何变换的，由于我们是单目slam，尺度漂移几乎是不可避免的，因此如果在这么"大"的一个尺度上，还是用se(3)，可能会导致两帧之间的变换不那么准确，因此我们放出一个尺度的自由度，使用sim(3)来衡量两帧之间的变换，也就是说，我们需要找到一个sim(3)群中的变换kesi，使得下面定义这个误差最小：

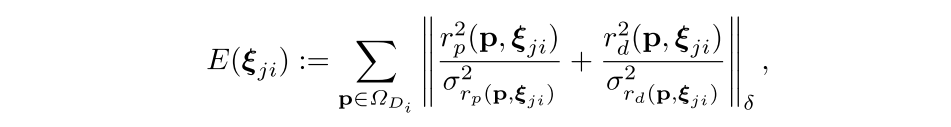
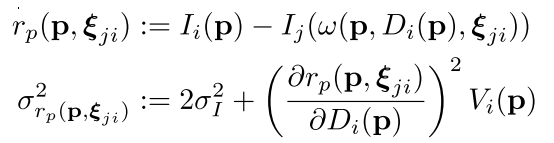
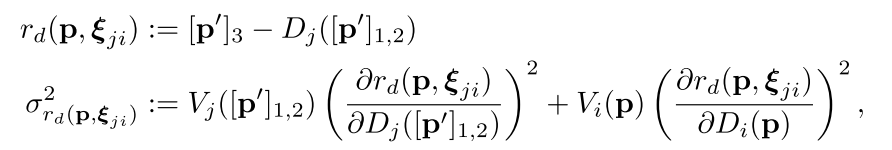
那么如何去寻找要插入的位置呢？方法很简单，首先去寻找所有可能相似的关键帧，并计算视觉意义上的相似度，之后对这些帧进行排序，得到最相似的那几帧，然后根据上面那个方程算出sim(3),相似度衡量公式:

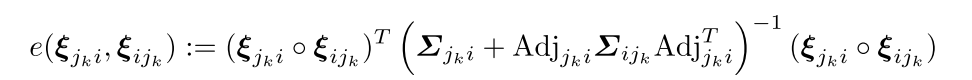
这里的邻接(Adj)关系在博客lsd-slam源码解读第一篇:Sophus/sophus中有详细介绍，请自行查看，注意Sigmod属于Sim(3)，为kesi的指数映射得到的转换矩阵
如果这个数值足够小(这个相似度足够高)，那么这一帧便插入map中，最后执行图优化(g2o)边为连接关系，节点为关键帧，即优化：

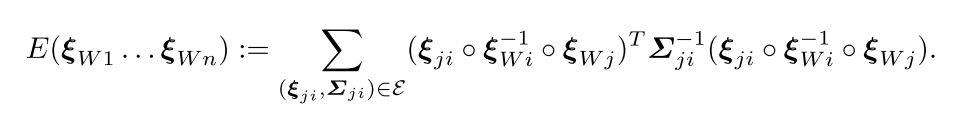
这便是lsd-slam算法的整体框架结构