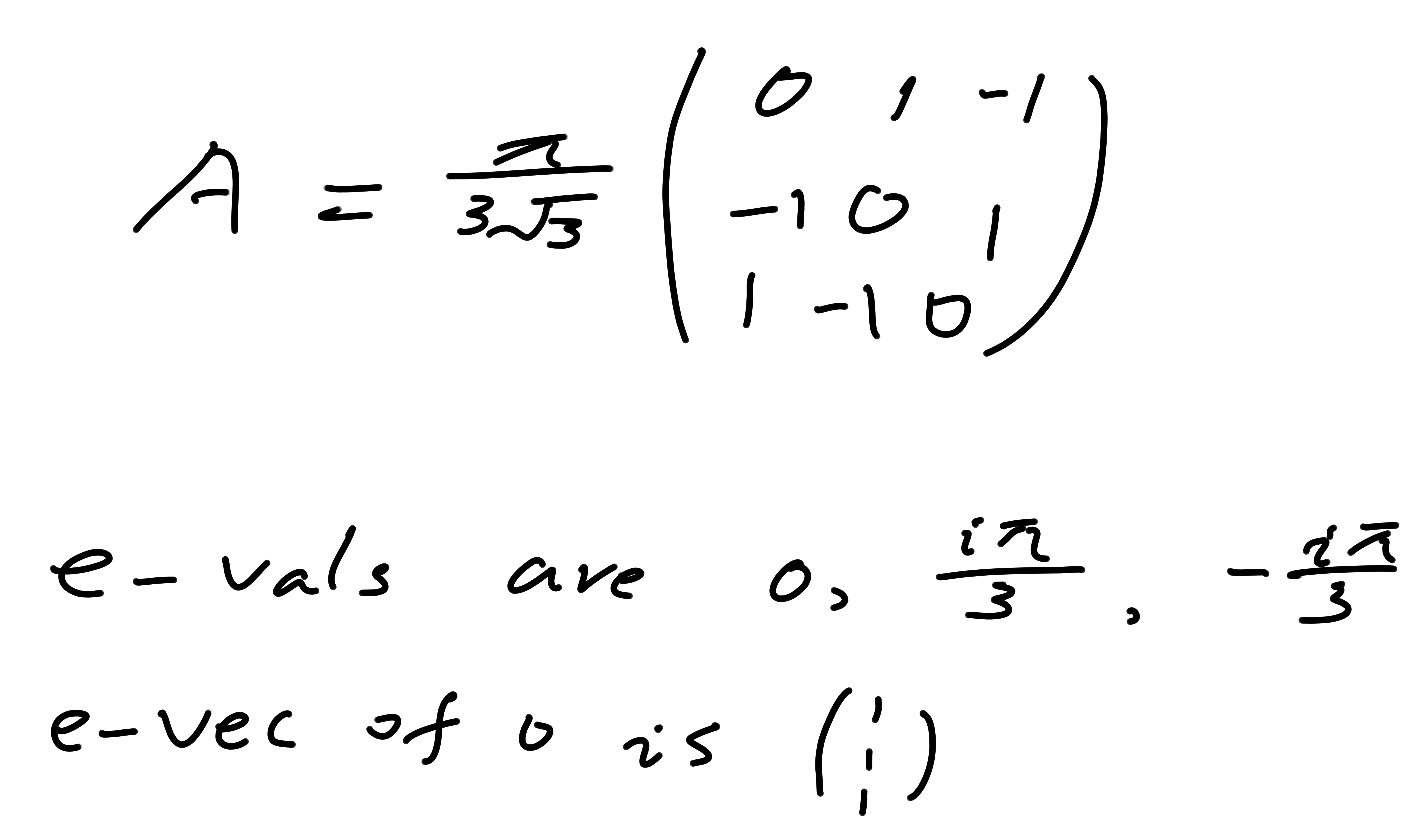SO(3) and so(3)

slam

SO(3) is the Group of rotatopns in $R^3$
= $\{3 \times 3\ orthogonal\ matrices\ with \ det = 1 \}$

so(3) = $\{3 \times 3\ anti-symmetric\ real matirces \}$ = Lie algebra of SO(3)

why group?

if $R, T\in SO(3)$,
then $R^{-1} = R^T, so (R^{-1})^TRT{-1}=RR^T = I$
and det$R^{-1}$ = det$R^T$ = det$R$ = 1

$(RT)^TRT = T^TR^TRT = T^T(R^TR)T = T^TT = I$
det$RT$ = det$R\times detT$ = 1

why Lie group

commutator(换位子或者交换子) of two matrices A, B is [A,B] = AB-BA

A(linear) Lie Algebra is a vector space of matrices that is closed under [,]

so(3) is a Lie algebra

proof

if A, B $\in$ so(3)
then A, B are real, and $A^T = -A, B^T=-B$
then $[A,B]^T = (AB-BA)^T = B^TA^T-A^TB^T = BA-AB = -[B,A]$
so [A,B] $\in$ so(3)

How are SO(3), so(3) related

If A $\in$ so(3), then $e^T \in$SO(3)

proof

$A^H = A^T = -A$
$(-iA)^H = iA^H=-iA$
so -iA is Hermitian
so $e^A = e^{i(-iA)}$ is unitary (the eigen value of Hermitian is real number, or according to spectral decomposition theorems, it is obviously that $e^A$ is unitary)
$e^A$ is real because A is real
if A = 0 then tr(A) = 0
then $e^A = e^{tr(A)} = 1$

eigenvalues

eigenvalues of A are 0, $i\theta$, $-i\theta$
then eigenvalues of $e^A$ are 1, $e^{i\theta}$, $e^{-i\theta}$

example