线性判别函数和判定面

模式分类

线性机

不知道你还记不记得前面讲过的判别函数的问题（见概述，贝叶斯策略，最大似然估计）
一个"判别函数"是指由x的各个分量的线性组合而成的函数: $g(x) = w^Tx + w_0$
这里$w$是"权向量"，$w_0$被称为"阈值权"或者"偏置"，一般情况下有c个这样的判别函数，分别对应c类中的一类，我们总是选取$g_i$取得最大值的那个类型（希望明白的是，这个是使得后验概率最大的那个类型，而有一种可能的线性判别函数是源于分布为正态分布，而且假设$\Sigma_i = \sigma^2I$）
其实上面那种定义判别函数得到的分类器叫做"线性机"，线性机把特征空间分为c个判决区域$R_i$($i = 1\ ...\ c$),当$x$在$R_i$中时，$g_i$取得最大值，如果$i \neq j, g_i = g_j$可以得到一个将$R_i$和$R_j$分开的超平面$H_{ij}$

实际上线性机的判决区域是凸的，是往往是单联通的，这使得它为条件概率密度$p(x|w_i)$为单峰的问题设计线性机是比较适合的

广义线性判别函数

实际上在线性判别函数$g(x) = w^Tx + w_0$加上额外的项，就可以很容易得到二次判别函数（考虑对应高斯分布是哪种情况）

$$g(x) = w_0 + \sum\limits_{i=1}^d\sum\limits_{j=1}^dw_{ij}x_ix_j\ （w_{ij} = w_{ji}）$$

甚至你可以加入更高次的项，于是可以愉快地得到多项式判别函数，实际上这可以看成某一种判别函数$g$的泰勒展开忽略更高阶的无穷小

$$g(x)=\sum\limits_{i=1}^\hat{d}a_iy_i(x)$$

或者

$$g(x)=a^Ty$$

这里a是$\hat{d}$维权向量，$\hat{d}$个分量函数$y_i(x)$，有时候被称为$\varphi$函数，可以是x的任意函数。这样的函数对应特征提取子系统的结果，通过巧妙选择这些函数，并使得$\hat{d}$足够大，就可以通过这样的展开来逼近任何想要的判决函数。
换句话说，就是你对原始数据做一个映射，映射到一个新的特征空间上，然后在特征空间进行线性判别，但实际上，如果维度过高，会带来很严重的"维度灾难"，使得它往往很难实际应用。

两类线性可分

假设我们有一个包含n个样本的集合，#y_1,y_2,\ ... \ y_n#，一些标记为#w_1#,另一些标记为$w_2$,我们希望这些样本确定判别函数$g(x)=a^Ty$的权向量$a$。我们有理由相信有一个解，它产生错误的概率非常小，那么很合理的想法是寻找一个能把这些样本都正确扥类的权向量。假如这个权向量存在，那么这些样本被称为“线性可分”的。
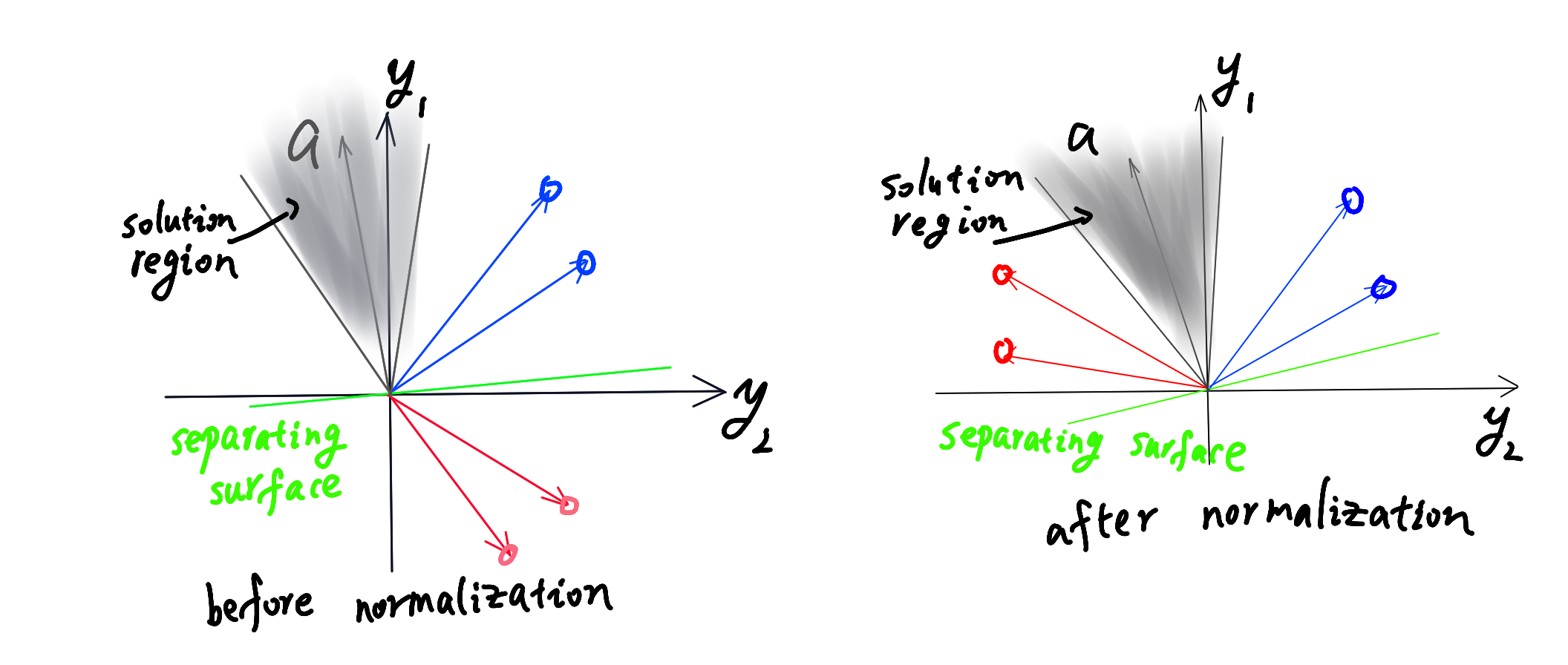
对于一个样本$y_i$，如果$a^Ty_i > 0$,就标记为$w_1$,如果$a^Ty_i < 0$,则标记为$w_2$，特别的，如果取了等号，就不做区分，这样我们可以用一种"规范化"(normalization)操作来简化两类样本的训练过程，也就是说属于$w_2$的样本，用负号表示，由此，我们寻找一个对于所有样本都有$a^Ty_i$向量$a$,这样的向量叫做“分离向量”(separating vector)更正规的说法是"解向量"(solution vector)

几何解释或术语

求解权向量的过程可认为是确定“权空间”(weight space)中的一点，每个样本都对解向量的可能位置给出限制。等式$a^Ty_i=0$确定了一个穿过权空间远点的超平面，$y_i$为其法向量。解向量，如果存在，必须在每个超平面的正侧，而且必须在N个正半空间的交叠区，而且该区域中的任意向量都是解向量，我们称这样的区域叫做“解区域”(solution region)，下面两图分别给出了规范化前和规范化后的解区域图像

感知器最小化原则

考虑构造解线性不等式$a^Ty_i>0$的准则函数问题，最显然的选择是假设$J(a;y_1,\ ... \ y_n)$为被$a$分成错的样本数，但是这个函数是个分段的常值函数(显然取值为自然数)，对梯度搜索不是一个很好的选择，一个更好的选择是令感知器准则函数(perceotron criterion function):

$$J_p(a) = \sum\limits_{y \in Y}(-a^Ty)$$

这里的$Y(a)$是被$a$分错的样本集(如果都分对了，显然$Y$是空集)，由于$a^Ty \ge 0$, 所以$J(a)$是非负的(从几何上知道，$J(a)$和分错样本到判决边界距离之和成正比的)我们可以轻松根据下列方程，让这个距离达到最小值

$$\nabla J_p = \sum\limits_{y \in Y}(-y) \\ a(k+1) = a(k) + \eta (k)\sum\limits_{y \in Y_k}y$$