隐马尔可夫模型的计算

模式分类

@author lancelot-vim

---

约定一些新的术语，并且将重新整理记号系统。通常把隐马尔可夫模型图称为有限状态机(finite state machine, FSM)，如果网络内部得转移都和概率相关，那么这样得网络叫做马尔可夫网络。这种网络是严格符合因果关系的，因为下一时刻状态的概率，之和上一时刻状态有关，如果只要选择好相应得合适得初始状态，每个特定得状态发生得概率都非0,那么这个马尔可夫模型就被成为"各态历经"的。最终状态或者吸收状态(final state or absorbing state)只系统一旦进入这个状态，就无法里还的情况(比如$a_{00} = 1$,则系统永远处于初始状态)

前文提到，用$a_{ij}$来表示隐状态之间得转移概率，用$b_{jk}$表示发出可见状态得概率：

• $a_{ij} = P(w_j(t+1)|w_i(t))$
• $b_{jk} = P(v_k(t) | w_j(t))$

我们要求在每一时刻都必须准备好转移到下一时刻，同时要发出一个可见的符号，这样有归一化条件:

$$\sum\limits_ja_{ij} = 1 \\ \sum\limits_kb_{jk} = 1$$

定义了这些术语后，使得我们可以关注下列3个隐马尔可夫模型得核心问题：

1. 估值问题：假设我们有一个HMM,其转移概率$a_{ij}$和$b_{jk}$已知，计算这个模型某一特定观测序列$V^T$得概率
2. 解码问题：假设我们已有一个HMM，和一个观测序列，决定最有可能产生这个观测序列得隐形状态序列$w^T$
3. 学习问题：假设我们知道一个HMM的大致结构（隐形状态参数数量、可见参数数量）如何从观测中得到$a_{ij}和b_{jk}$

---

估值问题

一个模型产生可见序列$V^T$得概率为：$P(V^T) = \sum \limits_{r=1}^{r_{max}} P(V^T|w_r^T)P(w_r^T)$
其中的r是每个特定长T的隐状态序列得下标:$w_r^T=\{w(1), w(2), \ ... \ ,w(T)\}$, 在c个不同隐状态下的情况下，为了计算这个特定可见状态序列$V^T$得概率，我们必须考虑每一种可能得隐状态序列，计算它们各自产生可见状态序列$V^T$的概率，然后进行相加，所以序列概率就是对应得转移概率$a_{ij}$和产生可见符号概率$b_{jk}$的乘积。

由于这里处理的是一阶马尔可夫过程，所以公式可以写为:$P(w^T_r)=\prod\limits_{t=1}^{T}P(w(t)|w(t-1))$,也就是序列中的转移概率依次相乘，在上式中，$w(T) = w_0$为最终的吸收概率，其产生的唯一得独特可见符号为$v_0$，在语音识别中，$w_0$往往代表一个空状态，或者没有发声音的状态，符号$v_0$就表示静音

由于已经假设可见符号的概率只依赖于这个时刻所处得隐状态，因此，$P(V^T|w_r^T) = \prod \limits_{t=1}^TP((v(t)|w(t))$,也就是把$b_{jk}$依次相乘，最终，我们可以得到:

$$P(V^T) = \sum \limits_{r = 1}^{r_{max}} \prod \limits_{t=1}^TP(v(t)|w(t))P(w(t)|w(t-1))$$

按照这个算法，时间复杂度为$O(c^TT)$，假如c = 10, T = 20，可见，几乎是无法实现的，实际上有个可行得代替方案，递归计算$P(V^T)$,由于每一项$P(v(t)|w(t))P(w(t)|w(t-1))$只涉及到$v(t),w(t)和w(t-1)$，我们定义：

$$\alpha_j(t) = \left \{ \begin{array} 00 & t=0 且 j \neq 初始状态 \\ 1 &t = 0 且 j = 初始状态 \\ \sum_i \alpha_i(t-1)a_{ij}b_{jk}v(t) & 其他 \end{array} \right.$$

其中$b_{jk}v(t)$表示t时刻的可见状态$v(t)$确定的转移概率$b_{jk}$, 因此，只需要对具有可见状态$v(t)$得索引k得项求和即可，$\alpha(t)$表示我们的HMM在t时刻，位于隐状态$w_j$，并且已经产生了可见序列$V^T$的前t个符号的概率。

HMM向前算法

1. initialize t <- 0, $a_{ij}, b_{jk}, V^T, \alpha_j(0) = 1$
2. repeat t <- t+1
3. $\quad a_j(t)$ <- $b_{jk}v(t)\sum \limits_{t=1}^c \alpha_i(t-1)a_{ij}$
4. until t = T
5. return $P(V^T)$ <- 最终状态得$a_0(T)$
6. end

算法示意图：

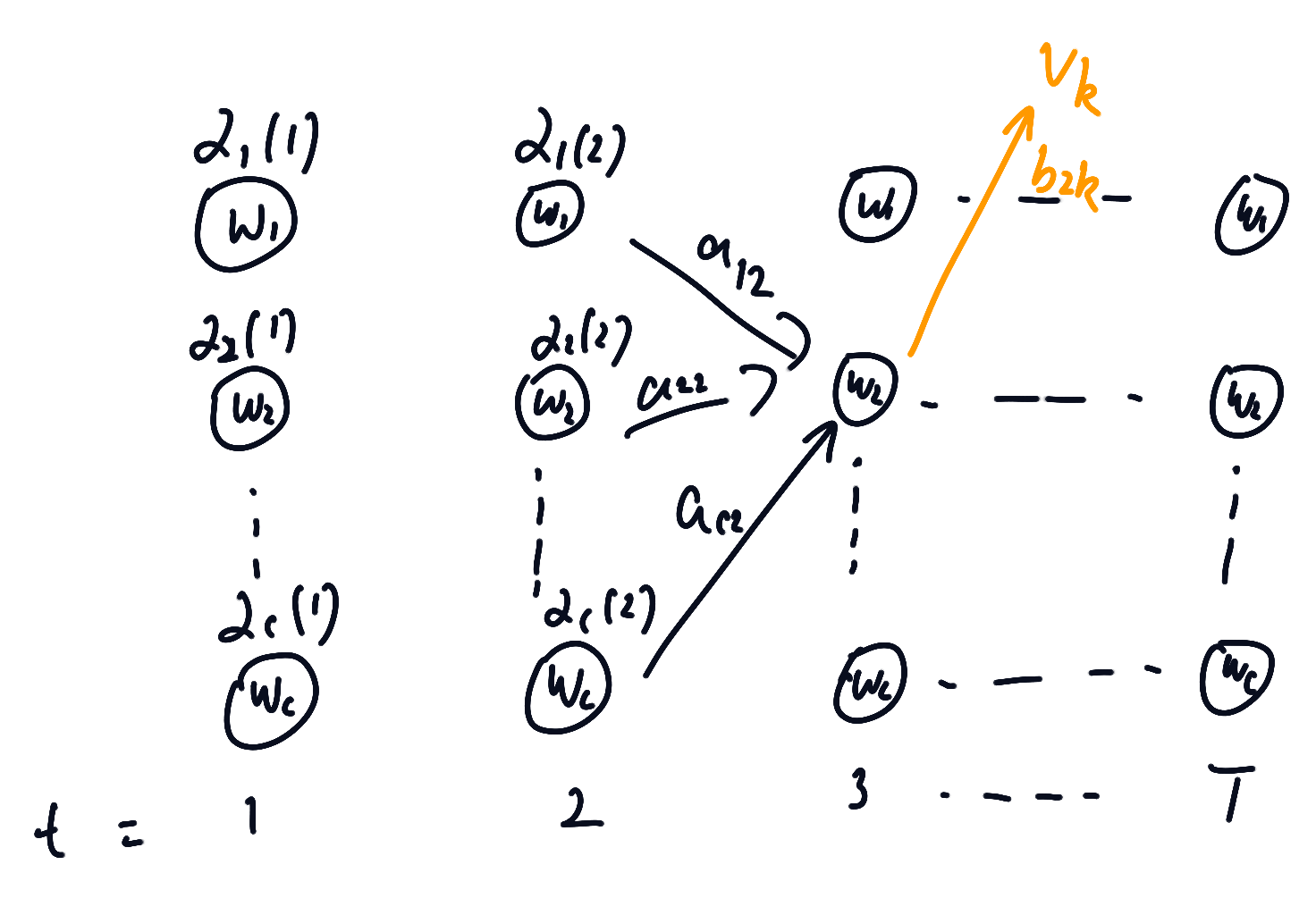
这个算法的时间复杂度为$O(c^2T)$，在实际应用中使用特别广泛

---

一个小例子

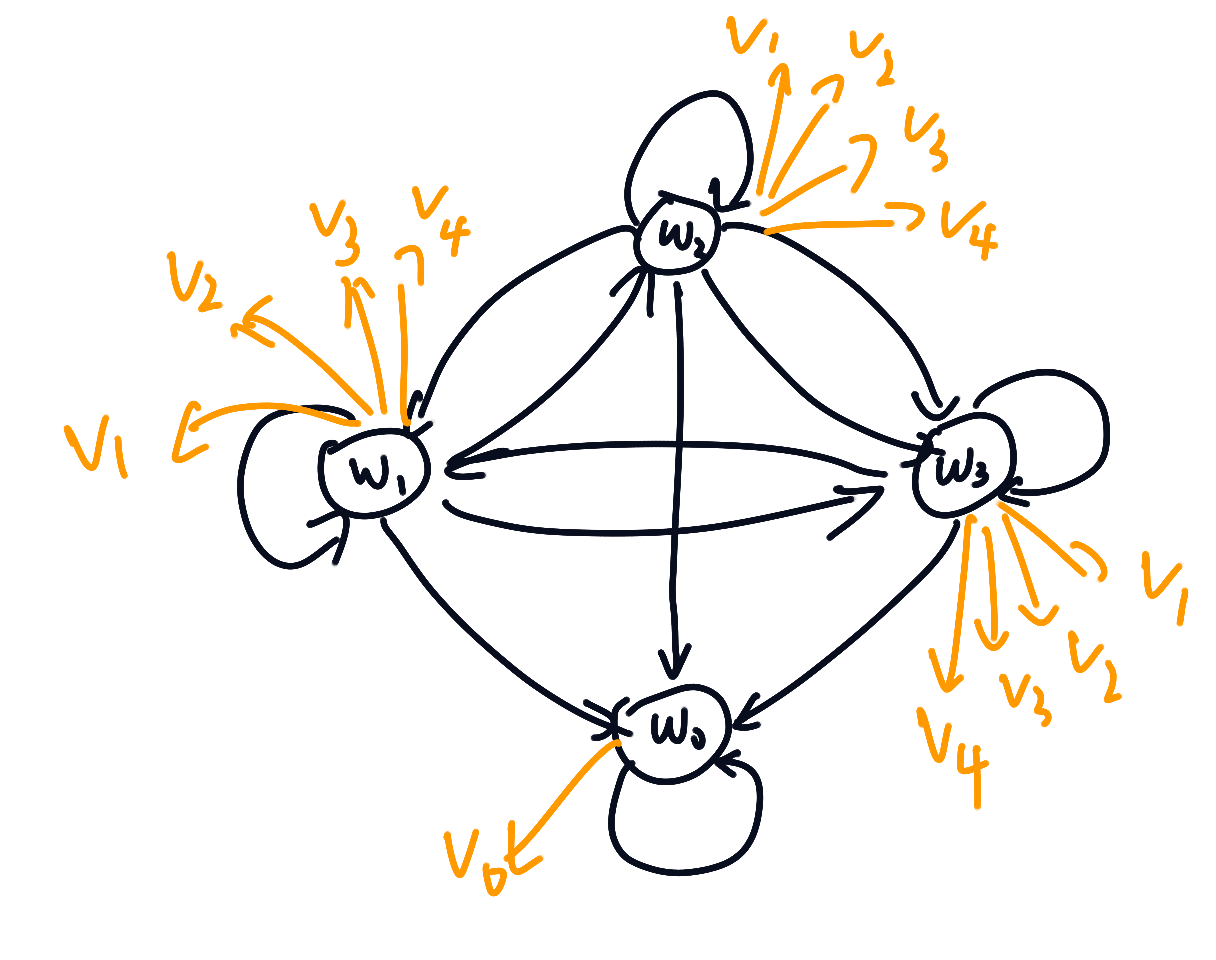
如图所示的HMM，他具有一个明确得吸收状态和唯一的独特空可见符号$v_0$，转移矩阵如下：

$$a = \left ( \begin{array} 01 & 0 & 0 & 0 \\ 0.2 & 0.3 & 0.1 &0.4 \\ 0.2 & 0.5 & 0.2 & 0.1 \\ 0.8 & 0.1 & 0.0 & 0.1 \end{array} \right )$$
$$b = \left ( \begin{array} 01 &0 &0 &0 &0 \\ 0 & 0.3 & 0.4 & 0.1 & 0.2 \\ 0 & 0.1 & 0.1 & 0.7 & 0.1 \\ 0 & 0.5 & 0.2 & 0.1 & 0.2 \end{array} \right)$$

计算观测序列为:$V^4 = \{v_1, v_2, v_2, v_0 \}$的概率

如下图所示，假设在t=0时刻，系统的隐状态为$w_1$，每一步的可见符号为第一行，$\alpha_i(t)$的数值在圆圈中已经表示出，$a_{ij}b_{jk}$按照步骤t=1到t=2已经标出

---

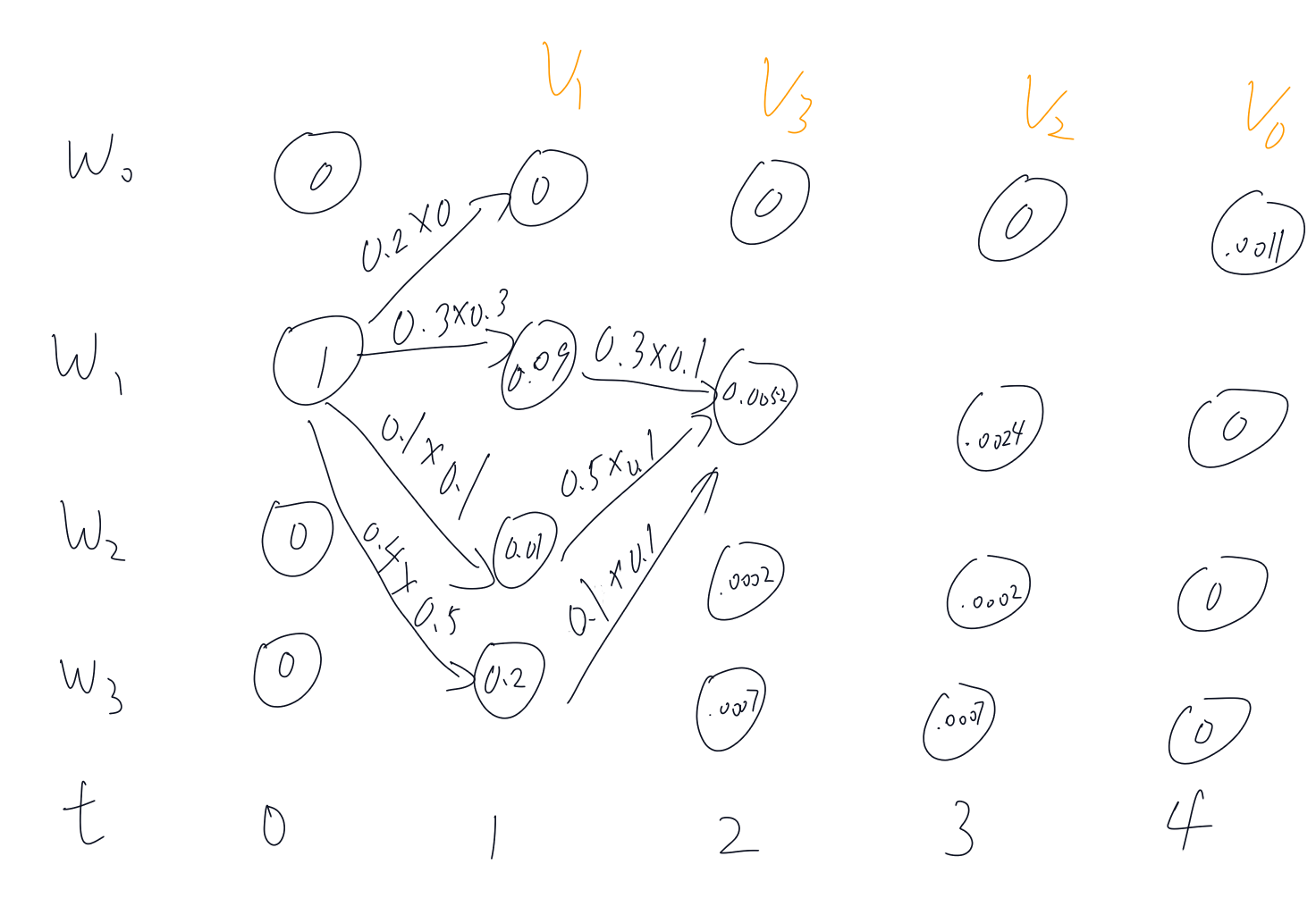
解码问题

所谓解码问题，就是已知观测序列$V^T$，求解最可能得隐状态序列得过程，算法如下：

HMM解码算法

1. begin initialize Path <- {}, t = 0
2. $\quad$ repeat t <- t + 1
3. $\qquad$ j <- 1
4. $\qquad$ repeat j <- j + 1
5. $\quad \qquad$ $\alpha_j(t)$ <- $b_{jk}v(t) \sum \limits_{i = 1}^c \alpha_i(t-1)a_{ij}$
6. $\qquad$ until j == c
7. $\qquad$ j' <- argmax $\alpha_j(t)$
8. $\qquad$ 将$w_j$添加到Path
9. $\quad$ until t = T
10. $\quad$ return Path
11. end

解码算法是一个贪心的策略，每次选择当前概率最大的$\alpha_j$为最优策略，这个可能导致无法达到全局最优解，甚至可能会出现一些无法存在得错解。

---

学习问题

学习问题是根据观察值(或者说训练样本)确定转移概率$a_{jk}和b_{jk}$，到目前为止，还没有能够根据训练样本确定最优参数集合的方法，但是，通过一种非常直接的方法，我们几乎总能得到一个足够令人满意的解答

向前-向后算法

我们定义$\beta_i(t)$为在t时刻位于状态$w_i(T)$，并且将产生t时刻之后的目标序列的概率(时间范围为t+1->T):

$$\beta_i(t) = \left \{ \begin{array} 00 & w_i(t) \neq w_0 且t = T\\ 1 & w_i(t) = w_0 i且t = T \\ \sum_j \beta_j(t+1)a_{ij}b_{jk}v(t+1) & 其他 \end{array} \right.$$

定义从状态$w_i(t-1)$转移到$w_i(t)$的条件概率为$\gamma_{ij}(t)$

$$\gamma_{ij}(t) = \frac{\alpha_i(t-1)a_{ij}b_{jk}\beta_j(t)}{P(V^T|\theta)}$$

• 分子代表：产生$V^T$中前t-1个状态和后t个状态时，从t-1状态由$w_i(t-1)$转换到$w_j(t)$的概率
• 分母代表：$P(V^T|\theta)$是模型产生可见序列$V^T$的概率
• $\gamma_{ij}$代表：在模型产生$V^T$序列时，状态$w_i(t-1)$转移到w(t)的概率

由此可得：
1. 在任意时刻，状态$w_i$到状态$w_j$的转换预计值为:$\sum \limits_{t=1}^T\gamma_{ij}(t)$
2. 在任意时刻，状态$w_i$发生转换概率预计值为:$\sum \limits_{t=1}^T \sum_k \gamma_{ik}(t)$
3. 在任意时刻，状态$w_i$到状态$w_j$的转换后，观测值为$v_k$的预计值为: $\sum \limits_{i=1}^T\sum_{l,v(t) = v_k}\gamma_{jl}(t)$
4. 在任意时刻，状态$w_i$到状态$w_j$的转换后,得到所有观测预计值为$\sum \limits_{i=1}^T\sum_{l}\gamma_{jl}(t)$

所以，得到$\hat{a}_{ij}，\hat{b}_{jk}$为:

$$\hat{a}_{ij} = \frac{\sum \limits_{t=1}^T\gamma_{ij}(t)}{\sum \limits_{t=1}^T \sum_k \gamma_{ik}(t)} \qquad \qquad (1)\\ \\ \hat{b}_{jk} = \frac{\sum \limits_{i=1}^T\sum_{l,v(t) = v_k}\gamma_{jl}(t)}{\sum \limits_{i=1}^T\sum_{l}\gamma_{jl}(t)} \qquad (2)$$

有了这两个估计值，我们可以通过大量样本，是用以上公式对模型逐步更新，直到收敛为止，这就是著名的Baum-Welch算法：

Baum-Welch算法(向前向后算法)

1. begin initialize $\ a_{ij}, b_{jk}$,训练样本$V^T$,收敛判据$\theta$, z <- 0
2. $\quad$ do z <- z + 1
3. $\qquad$ 通过a(z-1),b(z-1)，由(1)计算$\hat{a}(z)$
4. $\qquad$ 通过a(z-1),b(z-1)，由(2)计算$\hat{b}(z)$
5. $\qquad$ $a_{ij}(z)$ <- $\hat{a}_{ij}(z-1)$
6. $\qquad$ $b_{ij}(z)$ <- $\hat{b}_{ij}(z-1)$
7. $\quad$ until max[$a_{ij}(z) - a_{ij}(z-1), b_{jk}(z) - b_{jk}(z-1)$]
8. $\quad$ return $a_{ij}$ <- $a_{ij}(z)$, $b_{jk}$ <- $b_{jk}(z)$
9. end