切空间距离

模式分类

在很多分类算法中，如果不加考虑地随意选择距离度量，会存在很多问题。例如，对于knn算法，如果不加考虑地使用了欧几里得距离即$d = \sqrt{\sum|x_i - y_i|^2}$，那么在这个问题上可能给你带来毁灭性的结果。
$\qquad \qquad \qquad \qquad \qquad$
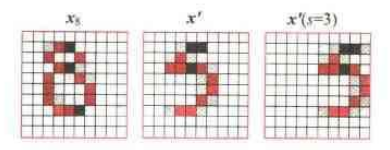
如上图所示，如果手写体5向右移动了3像素的距离，这样显然会给分类带来巨大的误差，可以想象的是，欧几里得距离无论是在处理平移，旋转还是尺度变换，甚至是线条粗细，都会给分类器带来巨大的影响。

对此，我们要选取一个新的距离，设法克服以上缺陷，这个距离就是"切空间距离"，简称"切距"。

假设我们已经知道所需处理的问题会涉及r种变换，比如水平平移，垂直平移，剪切，旋转，尺度变换，线条细化等，在设计分类器时，我们对每一个原型样本$x'$,都进行每一种操作$\mathcal{F}_i(x';\alpha_i)$,这样就能代表图像经过某种变换得到新的图像的变换过程，比如图像$x'$旋转角度$\alpha_i$等等，然后对于每一种变换，我们都构造一个切向量$TV_i$

$$TV_i = \mathcal{F}_i(x'; \alpha_i) - x'$$

这个计算只需要进行一次就够了，而且在训练过程并没有对时间有严格限制，这样对每一个原型样本，构造$r\times d$的矩阵$T$，这个矩阵由$x'$处的切向量组成，这些向量是线性无关的，必须指出的是这个算法对二值图无效，因为二值图求导运算无法定义，如果要处理二值图，需要进行平滑处理。

最后，我们转而计算一个测试点$x$模型原点$x'$之间的切空间距离，如果矩阵$T$由$x'$的r个切向量组成，那么测试点$x'$到原型样本点$x$的距离为：

$$D_{tan}(x',x) = \min\limits_a[||(x'-Ta)-x||]$$

用这个距离，可以保证只要图像是这r种变换之中的一种，对于分类器来说，这些变换都不会对分类带来多少影响，因为总是在搜索a，让这个距离最小，而a正好是变换的参数，得到这个最小距离，就好像找到了我们对图像做了某个变换之后的那个特征之间的距离一样，这个时候便把这些变换的影响给消除了