隐马尔可夫模型

模式分类

@author lancelot-vim

在一些与时间相关的问题中，我们会遇到t时刻发生的事件受t-1时刻发生事件的直接影响，处理这些问题时，隐马尔可夫模型(hidden markov model, HMM)得到了最好的应用，例如在语音识别或者手势识别领域，隐马尔可夫模型具有一组已经设计好的参数，他们可以最好地解释特定类别中的样本。在使用中，一个测试样本被归类为能产生最大后验概率的那个类别，也就是说，这个类别的模型最好地解释了这个测试样本。

一阶马尔可夫模型

考虑连续时间上的一系列状态，在t时刻的状态被记为$w(t)$，一个(在时间长度上)为T的状态序列记为$w^T = \{w(1), w(2), \ ...\ , w(T)\}$,比如我们可能有$w^6 = \{w_1, w_4, w_2, w_2, w_1, w_4\}$，系统在不同时刻可以处于同一状态，但同一时刻不要求所有状态都被取到。

产生数据的机理是通过转移概率，记为$P(w_j(t+1) | w_i(t)) = a_{ij}$,表示系统在某一时刻处于状态$w_{i}$的情况下，下一时刻为$w_j$的概率，这个概率是与时间无关的，即$a_{ij}$是个常数，我们不需要$a_{ij} = a_{ji}$,而且，有可能前后两个时刻都处于同一状态中，即$a_{ii} \neq 0$，如图所示：

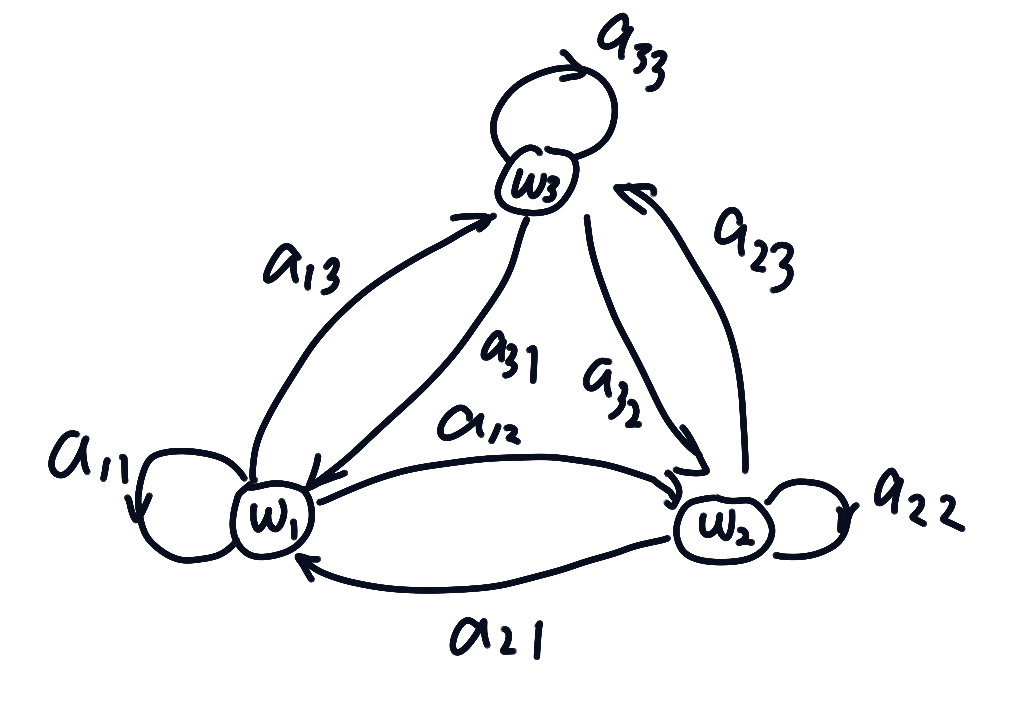
假设已有模型$\theta$,即全部转移概率$a_{ij}$已知，并且还知道某一特定序列$w^T$，为了计算该模型产生这个特定序列的概率，我们需要做的仅仅是吧连续的转移概率相乘，例如计算产生上述序列的概率，我们有$P(w^6 | \theta) = a_{14} a_{42} a_{22} a_{21} a_{14}$,假如知道了第一个状态的先验概率，那么就能计算出完整的产生该序列的概率。

到目前为止，我们讨论的是一阶马尔可夫模型，因为某一时刻的概率仅仅和前一时刻有关，但是人们可能不能直接观测到某些状态，比如单词"cat",需要从音标/k/转移到/a/，再转移到/t/，但人们往往只能听到发音而感受不到这些特定的状态，所以我们需要改变当前讨论的模型，引入"可见状态"(visible state)——即那些可以观测到的外部状态，和状态$w$——那些不能直接观测到的内部状态。

一阶隐马尔可夫模型

假设在某一时刻t,系统都处于某个状态$w(t)$中，这个系统还激发出某种可见的符号$v(t)$,虽然复杂的马尔可夫模型允许每一时刻发出的是连续函数(比如功率谱)，但这里为了简单起见，我们考虑离散符号的情形。我们把可见状态序列记为$V^T={v(1), v(2), \ ... \ , v(T)}$，那么工作过程如下：
在t时刻的状态$w(t)$下，没一个可能发出的状态$v_k(t)$都有相应的概率，记为$P(v_k(t) | wj(t)) = b_{jk}$,因为我们只能观测到可见状态，因此我们并不能知道内部处于哪个状态，所以这个模型叫做"隐马尔可夫模型"，如图所示：

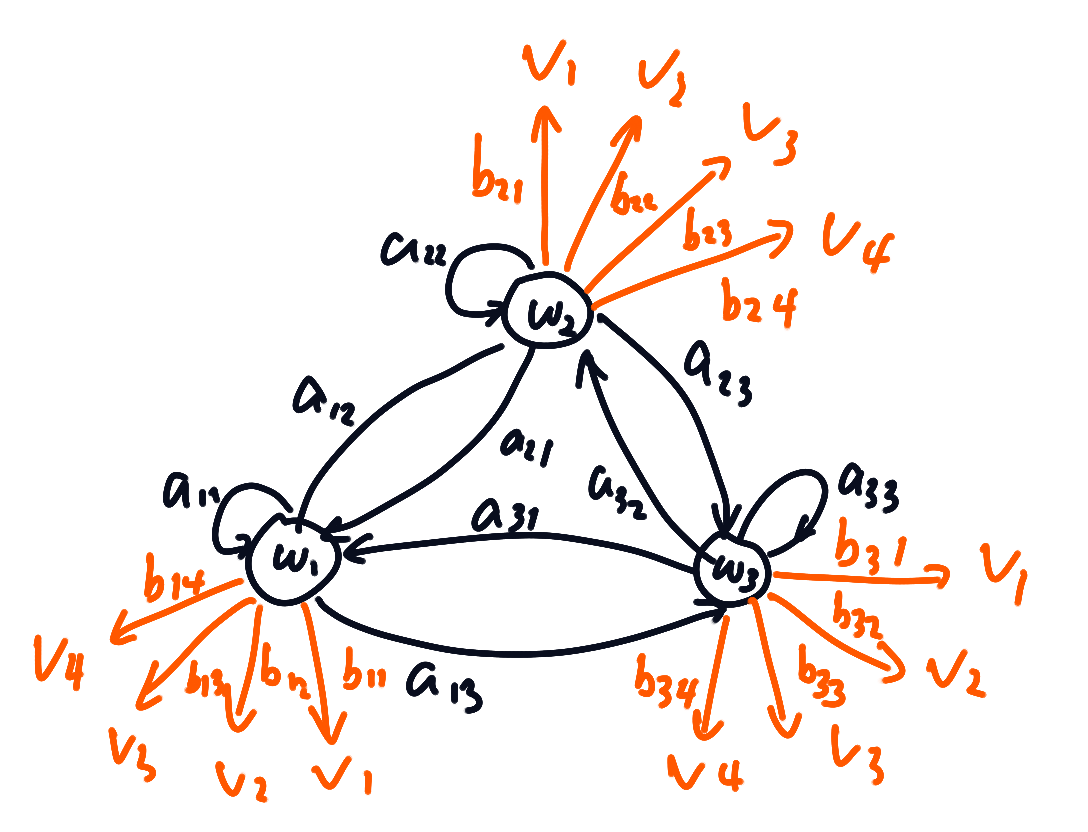
下一篇： 一阶隐形马尔可夫模型的计算