mmdetection最小复刻版(八)：梯度均衡机制GHM深入分析

mmdetection

0 摘要

论文题目：Gradient Harmonized Single-stage Detector
论文地址：https://arxiv.org/abs/1811.05181

GHM简单来说就是：正负样本不平衡和难易样本不平衡问题可以通过梯度均衡化机制解决。其本质和focal loss对易样本进行指数降低权重思想一样，但focal loss是从loss角度出发，但是ghm从梯度范数角度出发，不仅仅实现了focal loss效果，而且还具备克服外点样本影响。

一图胜千言：

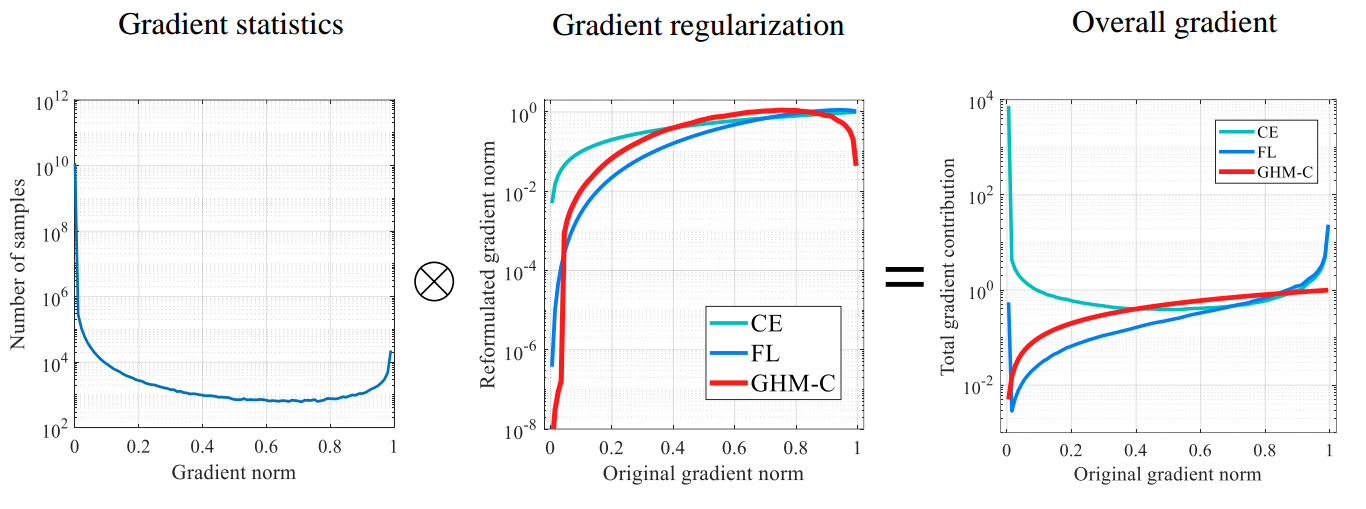
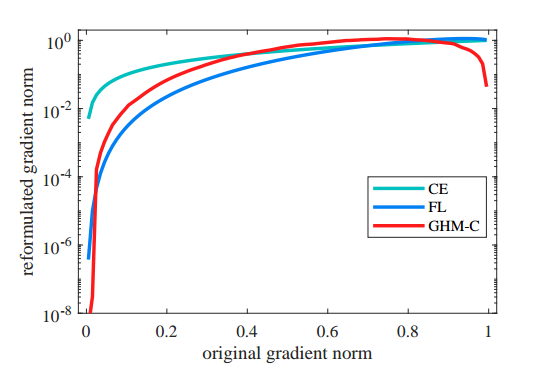
暂时抛弃梯度均衡化思想。如上图所示，可以简单等效认为横坐标的gradient norm是loss值，loss=0表示预测完全正确，loss=1表示预测完全错误

• 最左边图的纵坐标表示样本数目，从该图可以看出，对于一个已经收敛的模型，大部分样本都是易学习样本(并且大部分是背景样本)，但是依然有部分样本loss接近1，这些样本极可能是外点数据即标注有错误的数据，如果训练时候强行拟合，对最终性能反而有影响
• 中间图的纵坐标可能简单认为就是梯度值，在focal loss论文中我们知道，由于one-stage算法存在非常严重的难易样本不平衡问题，采用ce loss会导致梯度被大量易学习样本主导，而focal loss的做法就是把易学习样本的权重降低，这样达到loss平衡，但是其没有克服外点数据的左右，反映在图中就是在loss接近1的时候，梯度值非常大，这可以认为是一个弊端，最好的做法应该是红线所示，对loss两端的梯度进行降低权重
• 最右边图是最终效果，可以发现红线具备了易学习样本减低权重并且外点数据梯度不会过大的效果

一句话：focal loss虽然降低了大量易学习样本权重，但是没有处理外点样本，而GHM机制通过梯度分布角度进行均衡，解决了上述两个问题，效果更好。

但是GHM的缺点是通用性没有focal loss广泛，因为其内部需要定义梯度范数函数，不同的loss函数可能需要自己重新定义，论文中以常用的ce loss和smooth l1进行举例。

贴一下github:
https://github.com/hhaAndroid/mmdetection-mini
欢迎star

1 梯度均衡机制GHM

1.1 分类问题

以二分类bce loss为例

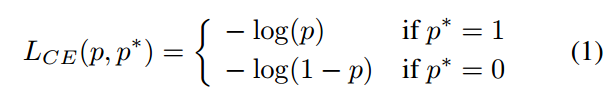
p是预测概率值，范围是0-1，p*是label，非0即1,其梯度函数为：

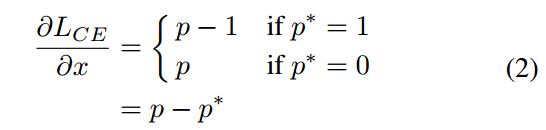
注意p=sigmoid(x),有了梯度公式，我们可以定义梯度范数或者说梯度模长为：

对于一个已经收敛的目标检测模型而已，大量样本所构成的g分布为：

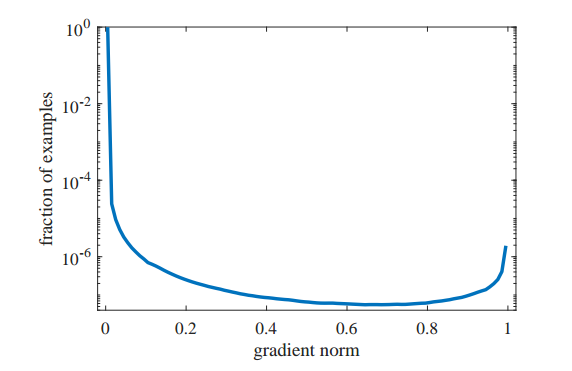
即大部分样本都是梯度范数比较小，对应易学习样本，但是依然存在很大一部分比例的梯度范数接近1，对应外点噪声数据。有了这个梯度分布图，做梯度均衡其实非常简单，只需要把这个分布倒过来例如变成1/g，然后作为样本权重即可，作者思想就是这样，只不过有些优化手段而已。

总之：对于任何一个loss函数，必须想办法得到梯度范数分布图才能进行后面的梯度均衡化操作，所以其通用性受到限制。

下面开始进行均衡化计算。对于分类问题ce loss而言，在得到g分布后，需要计算梯度密度函数：

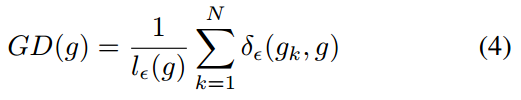
其中：

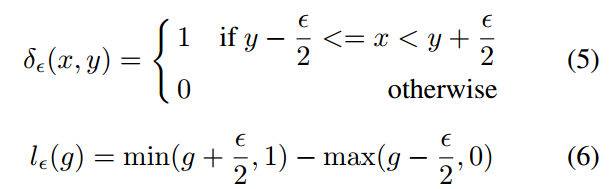
这个公式看起来比较抽象，其意思是设定梯度值分布间隔$\epsilon$，对g的纵坐标进行均匀切割，然后统计每个区间内的样本个数，除以横坐标区间长度即可。该密度函数可以反映出在某一梯度范数范围内的样本密度，或者说单位取值区域内分布的样本数量。其密度函数的形式应该和g长得差不多，但是已经从g对每个样本进行单独统计变成了GD对一区间内的样本进行统计了。

同时可以重写为对于一个样本，若它的梯度范数为g_k，它的密度就定义为处于它所在的区域内的样本数量除以这个单位区域的长度$\epsilon$

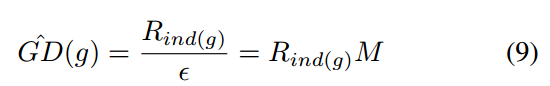
有了这个密度分布就好办了，其倒数就是样本loss的权值，密度值越大，权重越小，实现类似focal效应，而且由于外点数据的密度值也很大，故可以抑制外点样本影响。能够实现这种效果的原因是focal loss仅仅对每个样本单独进行计算，没有加入统计信息，而ghm机制考虑了密度。

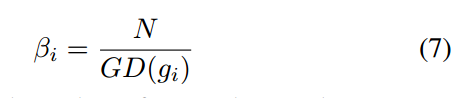
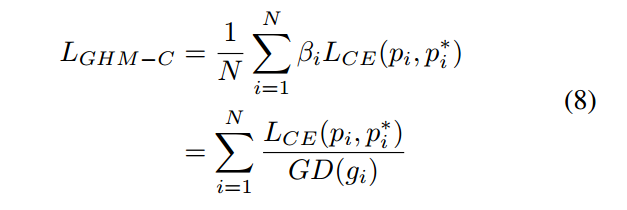
而且考虑到某些样本对梯度的波动，还引入了Exponential moving average(EMA)操作。

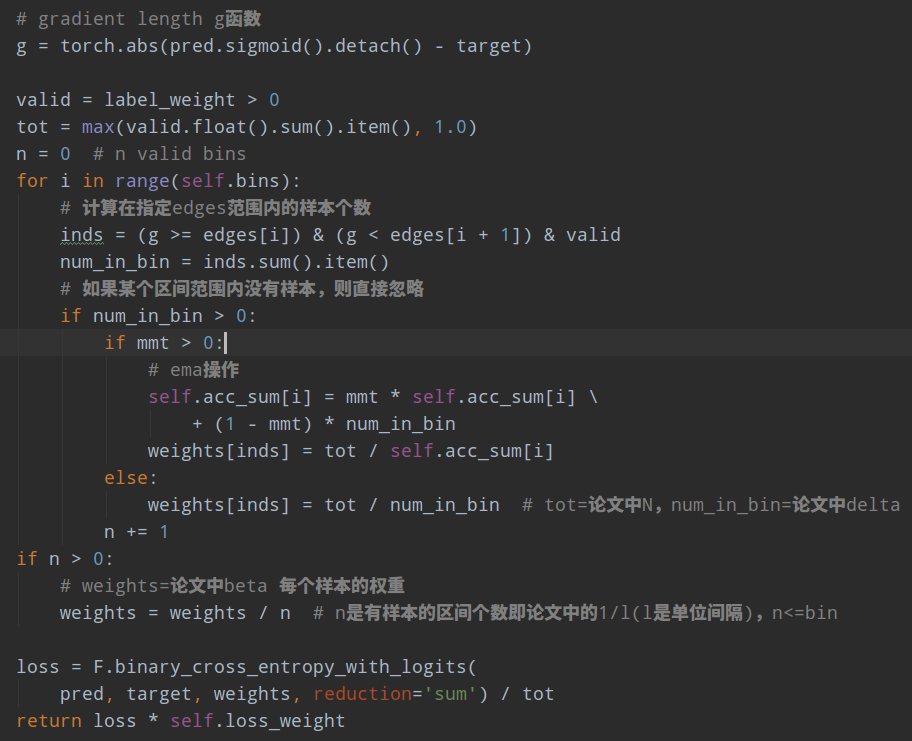
在mmdet里面是GHMC类，其代码逻辑为:

1. 设置间隔个数bin=30(论文中的M)，也就是把梯度范数函数值即纵坐标分成30个区间，区间范围是[0,1/30),[1/30,2/30)...
2. 计算总样本数tot=N
3. 遍历每个区间，计算g函数在指定区间范围内的样本个数num_in_bin即为delta；计算N/num_in_bin;如果要考虑ema,则在这一步进行
4. 所有样本权重都除以有效Bin个数n即有样本的区间个数，可能在某个区间范围没有任何样本，此时weights变量就是论文中的beta
5. 正常计算带权重的bce loss即可

1.2 回归问题

对于回归问题也是一样，主要是找出梯度范数函数g，找到g后，后续的操作是完全相同的。回归常用的loss是smooth l1，其定义如下：

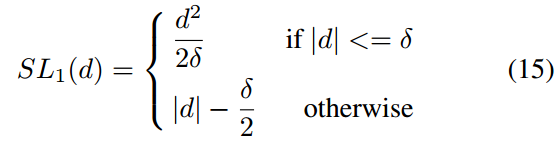
d是预测值和真实值的差，对其求导数：

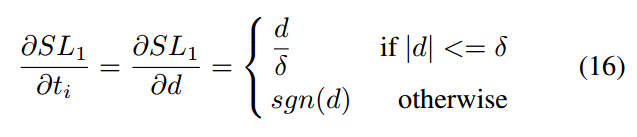
ti是某一个预测值，可以发现当差值大于指定范围后梯度是固定值，也就是无法反映难易程度，这就比较尴尬了，也就是说d无法作为梯度范数函数g，此时作者采用了等效公式ASL：

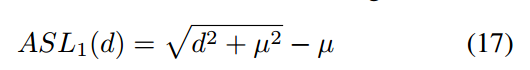
其梯度公式为：

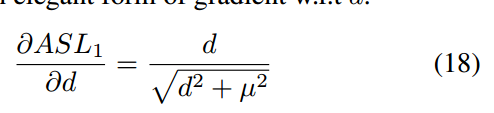
mu设置为0.02，修改了g函数如下所示：

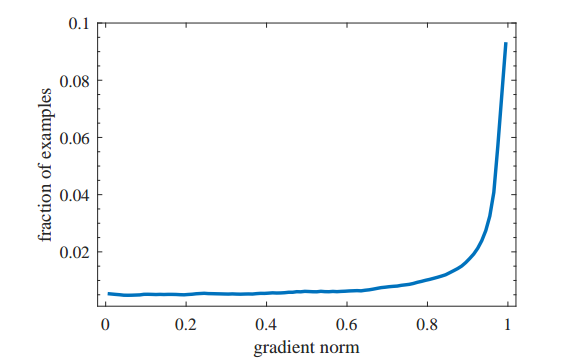
采用梯度密度函数进行梯度均衡化后，如下所示：

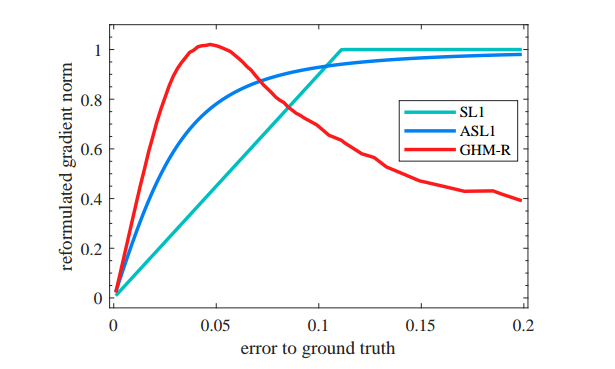
因为回归分支的输入全部是正样本，也就是说都是重要的样本，即使是易学习样本也不能随意的把权重降的很低，否则对最终性能有比较大的影响(在pisa论文里面也有分析)。

2 结果分析

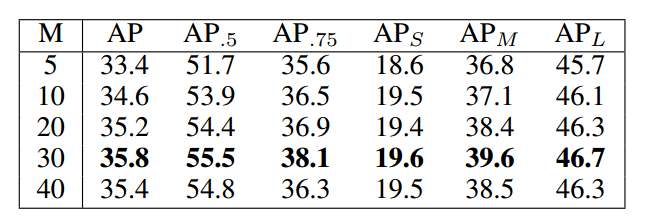
M表示对g进行划分区间的个数，M越大，划分的区间越多。实验表明该参数不能太小，否则失去了统计意义(权重都是趋于1，相当于没有)，M太大会导致切割的区间太多，密度函数统计就不准确了，效果可能会下降。

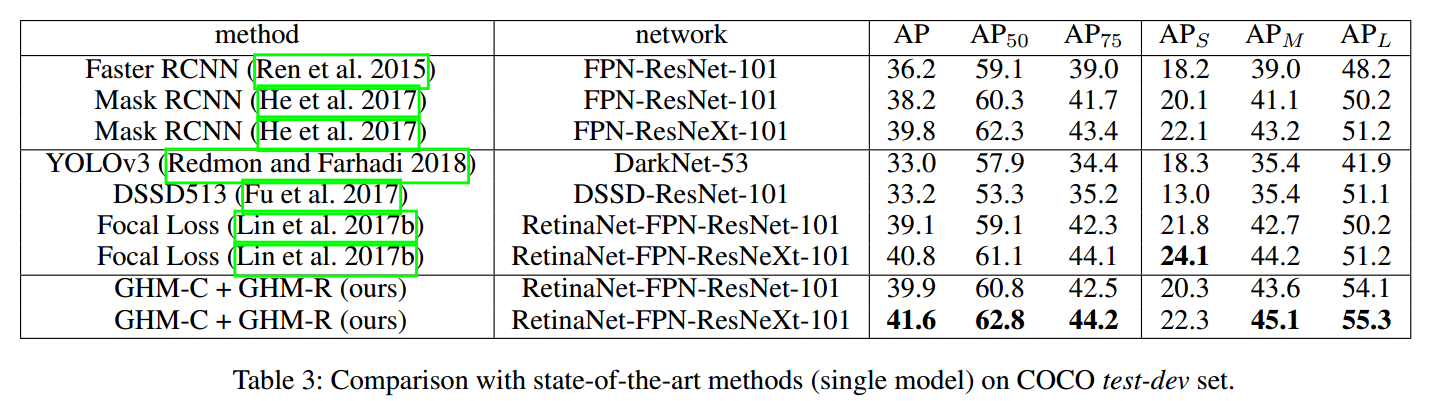
3 总结

纵观整个GHM算法，发现其思路其实非常简单，样本多的区域权重小一些就行，思想还是很不错的。但是一个比较大的问题是梯度范数函数g在不同的loss情况下都需要自己考虑清楚，对用户提出了比较高的要求，通用性比focal loss差一些。当然后面也出现了很多新的更加优异loss，留着我们在后面文章中慢慢分析吧。

贴一下github:
https://github.com/hhaAndroid/mmdetection-mini
欢迎star