卡特兰数

数论

定义

首先，卡特兰序列，他的通项公式为：；就叫做第n个Catalan数；
前几个Catalan数是：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, …

递推式：

Catalan数满足递归式：h(n) = h(1)*h(n-1) + h(2)*h(n-2) + ... + h(n-1)h(1) (n>=2);
该递推关系的解为：h(n) = C(2n-2,n-1)/n，n=1,2,3,...（其中C(2n-2,n-1)表示2n-2个中取n-1个的组合数）

相关问题：

1、给定n个数，有多少种出栈序列？
2、括号化问题。矩阵链乘： P=A1×A2×A3×……×An，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？
3、n个节点的二叉树有多少种构型？
4、将多边行划分为三角形问题。将一个凸多边形区域分成三角形区域(划分线不交叉)的方法数?

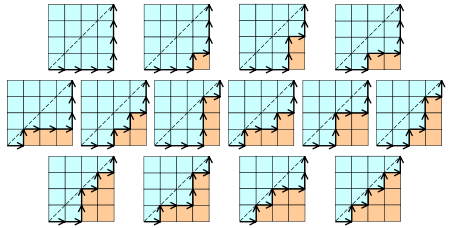
5、用n个长方形填充一个高度为n的阶梯状图形的方法个数？

6、在n*n的格子中，只在下三角行走，每次横或竖走一格，有多少中走法？

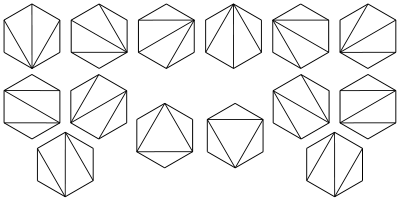
7、有n+1个叶子的满二叉树的个数？

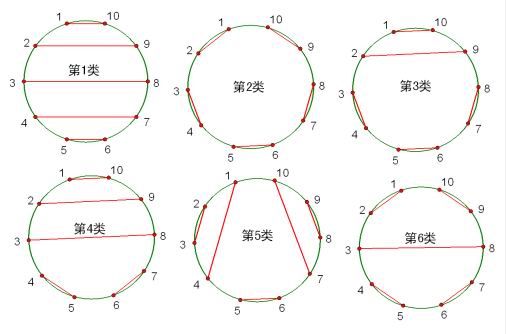
8、在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数？

代码

    h[0]=1;h[1]=1;
    for(int i=2;i<N+10;i++)
        for(int j=0;j<i;j++)
            h[i]+=h[j]*h[i-j-1];