评价分类器性能指标之AUC、ROC

机器学习

---

前言

本文内容大部分来自于如下两个博客：
http://blog.csdn.net/dinosoft/article/details/43114935
http://my.oschina.net/liangtee/blog/340317

引子

假设有下面两个分类器，哪个好？（样本中有A类样本90个，B 类样本10个。）

、	A类样本	B类样本	分类精度
分类器C1	A*90（100%）	A*10（0%）	90%
分类器C2	A*70 + B*20 （78%）	A*5 + B*5 （50%）	75%

分类器C1把所有的测试样本都分成了A类，分类器C2把A类的90个样本分对了70个，B类的10个样本分对了5个。

则C1的分类精度为 90%，C2的分类精度为75%，但直觉上，我们感觉C2更有用些。但是依照正确率来衡量的话，那么肯定C1的效果好一点。那么这和我们认为的是不一致的。也就是说，有些时候，仅仅依靠正确率是不妥当的。

我们还需要一个评价指标，能客观反映对正样本、负样本综合预测的能力，还要考虑消除样本倾斜的影响（其实就是归一化之类的思想，实际中很重要，比如pv总是远远大于click），这就是auc指标能解决的问题。

ROC

为了理解auc，我们需要先来弄懂ROC。
先来看一个普遍的二分类问题的结果，预测值和实际值有4种组合情况，看下面的表格：

我们定义一个变量：

$$true ~positive ~rate(TPR) = TP/(TP+FN = P)\\ false ~positive ~rate(FPR) = FP/(FP+TN = N)$$
看图也就可以知道，TPR表示的就是预测正确且实际分类为正的数量 与 所有正样本的数量的比例。--实际的正样本中，正确预测的比例是多少？

FPR表示的是预测错误且实际分类为负的数量 与所有负样本数量的比例。 --实际的负样本当中，错误预测的比例是多少？

可以代入到上面的两个分类器当中，可以得到下面的表格（分类器C1）：

、	预测A	预测B	合计
实际A	90	0	90
实际B	10	0	10

TPR = FPR = 1.0.

分类器C2：

、	预测A	预测B	合计
实际A	70	20	90
实际B	5	5	10

TPR = 0.78， FPR = 0.5

那么，以TPR为纵坐标，FPR为横坐标画图，可以得到：

上图中蓝色表示C1分类器，绿色表示C2分类器。可以知道，这个时候绿色的点比较靠近左上角，可以看做是分类效果较好。所以评估标准改为离左上角近的是好的分类器（考虑了正负样本的综合分类能力）。

一连串这样的点构成了一条曲线，该曲线就是ROC曲线。而ROC曲线下的面积就是AUC（Area under the curve of ROC）。这就是AUC指标的由来。

如何画ROC曲线

对于一个特定的分类器和测试数据集，显然只能得到一个分类结果，即一组FPR和TPR结果，而要得到一个曲线，我们实际上需要一系列FPR和TPR的值才能得到这样的曲线，这又是如何得到的呢？

可以通过分类器的一个重要功能“概率输出”，即表示分类器认为某个样本具有多大的概率属于正样本（或负样本），来动态调整一个样本是否属于正负样本（还记得当时阿里比赛的时候有一个表示被判定为正样本的概率的列么？）

假如我们已经得到了所有样本的概率输出（属于正样本的概率），现在的问题是如何改变这个阈值（概率输出）？我们根据每个测试样本属于正样本的概率值从大到小排序。下图是一个示例，图中共有20个测试样本，“Class”一栏表示每个测试样本真正的标签（p表示正样本，n表示负样本），“Score”表示每个测试样本属于正样本的概率。

接下来，我们从高到低，依次将“Score”值作为阈值，当测试样本属于正样本的概率大于或等于这个阈值时，我们认为它为正样本，否则为负样本。举例来说，对于图中的第4个样本，其“Score”值为0.6，那么样本1，2，3，4都被认为是正样本，因为它们的“Score”值都大于等于0.6，而其他样本则都认为是负样本。每次选取一个不同的阈值，我们就可以得到一组FPR和TPR，即ROC曲线上的一点。这样一来，我们一共得到了20组FPR和TPR的值，将它们画在ROC曲线的结果如下图：

当我们将阈值设置为1和0时，分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来，就得到了ROC曲线。当阈值取值越多，ROC曲线越平滑。

--在阿里比赛的时候还以为ROC是没用的！！！！真的是有眼无珠啊！！！还是有疑惑的是：如何根据ROC来判定结果的好换呢？看哪个分类器更加接近左上角吧。同时，可以根据ROC来确定划定正样本的概率边界选择在哪里比较合适！！！原来是这样！！！！！！！！！

为什么使用ROC

既然已经这么多评价标准，为什么还要使用ROC和AUC呢？因为ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化。下图是ROC曲线和Precision-Recall曲线的对比：

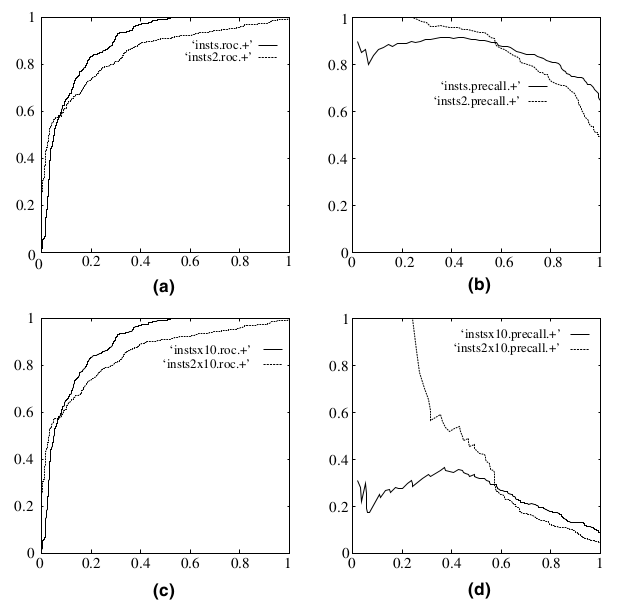
在上图中，(a)和(c)为ROC曲线，(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集（正负样本分布平衡）的结果，(c)和(d)是将测试集中负样本的数量增加到原来的10倍后，分类器的结果。可以明显的看出，ROC曲线基本保持原貌，而Precision-Recall曲线则变化较大。