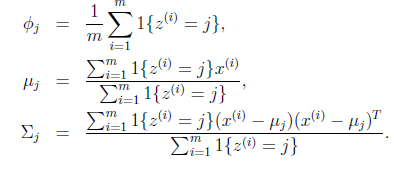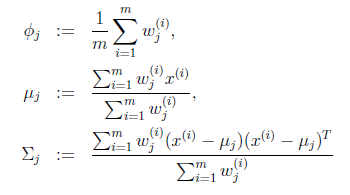3月机器学习班笔记第十二课--EM算法

机器学习

---

EM算法的入门

EM算法(Expectation Maximization Algorithm)即最大期望算法，它被评为机器学习十大算法之一。能评得上十大那一定很叼啊。该算法是一种以迭代的方式来解决一类特殊最大似然 (Maximum Likelihood) 问题的方法，这类问题通常是无法直接求得最优解，但是如果引入隐含变量，在已知隐含变量的值的情况下，就可以转化为简单的情况，直接求得最大似然的解。

作为了解EM的入门，推荐博客http://blog.csdn.net/zouxy09/article/details/8537620给大家，里面讲的生动形象，举例贴近生活。我呢，就盗用他的博客里面的一个示例作为引子，展开对EM的阐述：
我们接收到一个神圣的任务：需要去统计母校的男生女生的身高分布情况（假定服从高斯分布），即需要分别确定两个高斯分布中的参数$\mu_男、\sigma_男、\mu_女、\sigma_女$。怎么做呢？学校人数可有好几万呢，理智的选择是抽样。假设我们采访了100个男生100个女生，获取了200个关于身高的数据（包含性别这一栏）。有了这份数据，只需要分别对男生样本和女生样本使用极大似然估计（MLE），即可求得MLE下的参数$\mu_男、\sigma_男、\mu_女、\sigma_女$（具体过程略）。这本来是一件比较简单的任务，容易完成。

但是，和你一起统计数据的队友有些逗比，他不小心将200个统计数据中的性别这一栏给弄丢了（好吧，这样的队友也是醉了）。卧槽，这个时候怎么办？200个数据可是从两个不同的分布中抽取出来的（现在抽取得到的每个样本都不知道是从哪个分布抽取的），统一处理的话就不可能用MLE那么简单得解决了呀！唉，急死人！！

这个时候，你看到了EM算法。它用一种忽悠的语气对你说：“同学，既然没有明显的解决办法，倒不如你先随机猜测一下男生女生的这几个高斯分布参数吧，然后你再根据这个高斯分布来判断这200个数据更有可能属于哪一个分布。”你想:"这不是瞎扯淡么，怎么可以随便猜的？"但是没有其他办法，只有试试了。试试就试试。

将200个数据区分开男女生之后，你似乎知道怎么做了：“Y的，这个时候我不就可以使用MLE方法来重新估计这几个参数了么！”

EM算法说：“是的，更进一步的说，你有了这几个新的参数之后，就又可以将200个数据再次判断更有可能属于哪一个分布了，接着如此如此迭代，直到最后你可以得到一个较好的近似结果。”

迭代？！果然可以哦！ EM神秘一笑：“最后忠告：此方法得到的只是局部最优解哦，不一定是全局最优解。”随后扬长而去。

这个瞎比比的故事只是让我们对EM算法有了一个初步的印象。其中，“隐变量、迭代、局部最优”是较为核心的词汇。那么，接下来让我们从数学的角度来看看为什么EM算法是可行的。

EM的数学推导

首先是数学定义：假设我们有一个样本集$\{x^{(1)},...,x^{(m)}\}$，包含$m$个独立的样本。我们需要估计的参数为$\theta$。我们需要选择一个最佳的参数$\theta^*$,使得从训练样本集中观察到的情况出现的可能性最大，即极大似然估计，相应的对数极大似然函数（似然函数取对数即可）为：

$$l(\theta) = \sum_{i=1}^m log~p(x^{(i)};\theta)~~~~~(1)$$
现在引入一个隐含变量$z$，引入它的原因可能是方便实际问题的求解(如之前例子，不引入隐含变量根本无法求解)，也可能是变量具体含义的需求。那么带有隐含变量的对数极大似然估计为：
$$l(\theta) = \sum_{i=1}^m log\sum_{z^{(i)}}p(x^{(i)},z^{(i)};\theta)~~~~~(2)$$
由于现在的隐含变量$z^{(i)}$是未知的，直接使用极大似然估计去估计$\theta$会比较困难。但是，如果确定了$z^{(i)}$以后，求解就相对容易了。
从上式可以看到，$z^{(i)}$是随机变量，对每一个样本$x^{(i)}$求所有可能的$z^{(i)}$的联合概率密度之和，求和之后求对数。我们需要对“和的对数”求导然后令导数为0（MLE的作法），这个作法很复杂。如果能够转变为“对数的和”，那么对于求导而言就容易一点了。怎么做呢？看下面：
$$l(\theta) = \sum_{i=1}^m log\sum_{z^{(i)}} Q_i(z^{(i)}) \frac{ p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}~~~~~(3)\\ \geq \sum_{i=1}^m \sum_{z^{(i)}}Q_i(z^{(i)}) log~ \frac{ p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}~~~~~(4)$$
这个不等式转换就换成了“对数的和”，其中利用的是Jensen不等式的性质（点我查看凸优化一书中的讲解），考虑到$log(x)$是凹函数（二阶导小于0），而且$\sum_{z^{(i)}} Q_i(z^{(i)}) \frac{ p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$就是变量$\frac{ p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$关于随机变量$z^{(i)}$的期望。具体的Jensen不等式写成：
$$f(E_{z^{(i)}\thicksim Q_i}[\frac{ p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}]) \geq E_{z^{(i)}\thicksim Q_i} f([\frac{ p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}])~~~~~(5)$$
将f()使用log函数来表示即为(1)式到(2)式的由来。
这个过程可以看做是对$l(\theta)$求了下界。假定参数$\theta$的值已经给定，那么$l(\theta)$的下界值就取决于$Q_i$、$p(x^{(i)},z^{(i)})$这两项。我们希望通过对$Q_i$和$p(x^{(i)},z^{(i)})$的合理选择，得到一个更加紧的下界，以逼近$l(\theta)$的值。那怎样的下界才是好的呢？当然是不等式变成等式的时候。根据Jensen不等式，要想使得等式成立，条件是让随机变量变成常数值（不理解的话可以自己设一个凸函数，然后使用Jensen不等式来试试就知道了），即：
$$\frac{ p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} = c~~~~~(6)$$
其中$c$为常数，不依赖于$z_i$。我们知道$\sum_{z}Q_i(z^{(i)}) = 1$，那么也就有$\sum_{z}p(x^{(i)},z^{(i)};\theta) = c$(此处认为每个样本的两个概率比值都是$c$，多个等式分子分母相加不变)，那么有：
$$Q_i(z^{(i)}) = \frac{p(x^{(i)},z^{(i)};\theta)}{\sum_z p(x^{(i)},z^{(i)};\theta)} = \frac{p(x^{(i)},z^{(i)};\theta)}{ p(x^{(i)};\theta)} = p(z^{(i)}|x^{(i)};\theta)~~~~~(7)$$
值得注意的是，此处的$Q_i(z^{(i)})$是一个关于变量$z^{(i)}$的分布，但并不是变量$z^{(i)}$的先验分布。通过最终的表达式也可以知道，这是关于在已知$x^{(i)}$时的$z^{(i)}$的条件分布。

于是，我们得到了在固定参数$\theta$时，能够使得$l（\theta）$的下界尽可能大（即等于$l（\theta）$）的$Q_i(z^{(i)})$的计算公式。这一步就是EM算法中的E步。

接下来是M步，在给定$Q_i(z^{(i)})$后，调整$\theta$，去极大化$l（\theta）$的下界（在固定$Q_i(z^{(i)})$，下界还可以调整的更大）。由此EM算法的步骤如下：

为了对此有一个更深的印象，请看下面这幅图：

看图就可以知道，经过不断迭代，就可以得到使得对数似然函数$l(\theta)$最大化的参数$\theta$了。仅仅是看而已，我们还需要数学证明：这样的迭代过程会是收敛的么？
如何确保EM收敛？假定$\theta^{(t)}$和$\theta^{(t+1)}$是EM的第$t$次和第$t+1$次迭代后的结果。如果我们证明了$\theta^{(t)} \leq \theta^{(t+1)}$，也就是说极大似然估计在这个过程中单调增加，那么我们最后会得到极大似然估计的最大值。下面来证明，选定$\theta^{(t)}$后，我们得到E步：

$$Q_i^{(t)}(z^{(i)}) = p(z^{(i)}|x^{(i)};\theta^{(t)})~~~~~(8)$$
E步选择的$Q_i^{(t)}(z^{(i)})$保证了在给定$\theta^{(t)}$时，Jensen不等式中的等式成立，即：
$$l(\theta^{(t)}) = \sum_{i=1}^m \sum_{z^{(i)}} log~Q_i^{(t)}(z^{(i)}) \frac{ p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i^{(t)}(z^{(i)})}~~~~~(9)$$
然后进行M步，固定分布$Q_i^{(t)}(z^{(i)})$（此时的变量是$\theta$）,选择能够最大化对数似然函数的$\theta^{(t+1)}$，由此有：
$$l(\theta^{(t+1)}) \geq \sum_{i=1}^m \sum_{z^{(i)}} log~Q_i^{(t)}(z^{(i)}) \frac{ p(x^{(i)},z^{(i)};\theta^{(t+1)})}{Q_i^{(t)}(z^{(i)})} \\ \geq \sum_{i=1}^m \sum_{z^{(i)}} log~Q_i^{(t)}(z^{(i)}) \frac{ p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i^{(t)}(z^{(i)})} = l(\theta)~~~~~(10)$$
第一个不等式来自于似然函数l(\theta^{(t+1)})一直都是大于等于似然函数的下界（在$t+1$阶段什么时候取等号，在求得新的$Q_i^{(t+1)}(z^{(i)})$以及$\theta^{(t+1)}$时，此时只更新了$\theta^{(t+1)}$）。第二个不等式则侧面反映了M步的结果，$\theta^{(t+1)}$所对应的对数似然函数必然大于等于$\theta^{(t)}$的对数似然函数。
由此可以知道$l(\theta)$会单调上升，EM算法是收敛的。
实际上，如果我们定义
$$J(Q,\theta) = \sum_{i=1}^m \sum_{z^{(i)}} log~Q_i(z^{(i)}) \frac{ p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}~~~~~(11)$$
从前面的推导，可知$l(\theta) \geq J(Q,\theta)$，EM可以看做是J的坐标上升法：

E步：固定$\theta$，优化$Q$；
M步：固定$Q$，优化$\theta$；

形象表示如下图：

EM算法使用范例--混合高斯模型（GMM）

我们从最开始的调侃示例对EM有了初步了解，通过数学推导得到了确切的证明它能用，而且证明过程很聪明，不是么。现在我们想要使用这样的思想来解决一个广泛意义下的普遍问题--混合高斯模型。混合高斯模型是一种无监督学习算法，常用于聚类。当聚类问题中各个类别的尺寸不同，各类间有相关关系时，往往使用混合高斯模型更加合适（当然前提是各个类别之间可以看做是高斯分布）。值得注意的是：使用高斯模型得到的是属于某一类的概率，即所谓的"软聚类"。之前提到的估计学校男生女生身高的参数的问题就是这个模型的一个实例。
混合高斯模型的数学定义如下：
一如往常，假设我们有一个样本集$\{x^{(1)},...,x^{(m)}\}$，包含$m$个独立的样本。假设有一个隐含变量$z$，我们用它来表示隐含的类别标签。即样本$x^{(i)}$属于哪一个类别是未知的，但是具体样本$x^{(i)}$与具体类别$z^{(i)}$有一定的关联。该模型中有两个重要假设：

假设一：$z$服从多项式分布，即：

$$z^{(i)} \sim Multinomial(\phi)$$
其中，$\phi_j$表示的是概率$p(v = j)$，且有$\phi_j >0， \sum_j \phi_{j=1}^k =1$，$k$表示类别的数量。

假设二：已知$z^{(i)}$时，$x^{(i)}$满足高斯分布，即：

$$(x^{(i)}|z^{(i)}=j) \sim \mathcal{N}(\mu_j,\Sigma_j)$$
由此可得联合分布$P(x^{(i)},z^{(i)}) = P(x^{(i)}|z^{(i)})p(z^{(i)})$。

整个模型可以简单描述为：先从$k$个类别中按多项式分布抽取一个$z^{(i)}$，然后根据$z^{(i)}$所对应的高斯分布中生成一个样本$x^{(i)}$。
对数似然函数可以表示为：

$$l(\phi,\mu,\Sigma) = \sum_{i=1}^m log~p(x^{(i)},z^{(i)};\phi,\mu,\Sigma)\\ =\sum_{i=1}^mlog \sum_{z^{(i)}=1}^kP(x^{(i)}|z^{(i)};\mu,\Sigma)p(z^{(i)};\phi)$$
如果我们已经知道了每一个样本的所属类别$z^{(i)}$，那么上式就可以简化成：
$$l(\phi,\mu,\Sigma) = \sum_{i=1}^m[log~P(x^{(i)}|z^{(i)};\mu,\Sigma) +log~p(z^{(i)};\phi)]$$
进而可以使用MLE求得：

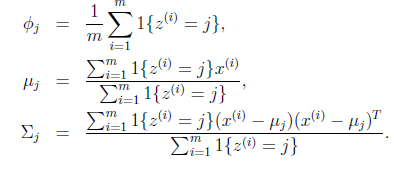
但是，我们实际上是不知道$z^{(i)}$的。只有使用EM算法。在E步，固定参数$\phi,\mu,\Sigma$，猜测隐含类型变量$z$。具体的，$z$的更新公式如下：对每一个$i,j$:

$$w^{(i)}_j = p(z^{(i)}=j|x^{(i)};\phi,\mu,\Sigma) =\frac{p(z^{(i)}=j,x^{(i)};\phi,\mu,\Sigma)}{p(x^{(i)};\phi,\mu,\Sigma)}= \frac{p(x^{(i)}|z^{(i)}=j;\mu,\Sigma)p(z^{(i)}=j;\phi)}{\sum_{l=1}^k p(x^{(i)}|z^{(i)}=l;\mu,\Sigma)p(z^{(i)}=l;\phi)}$$
这里的$w^{(i)}_j$也就是EM推导过程中的分布$Q_i(z^{(i)})$。其中，$p(x^{(i)}|z^{(i)}=j;\mu,\Sigma)$是已知模型参数下所得的正态分布，$p(z^{(i)}=j;\phi)$是多项式分布。由此可以得到给定样本$x^{(i)}$前提下，隐变量$z$的条件概率。

在M步，根据E步得到的$z$的分布，重新对参数进行极大似然估计。有：

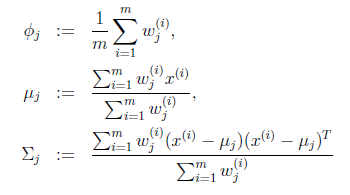
经过一定的迭代次数以后，最终问题得以解决。