@adamhand
2019-03-11T02:22:10.000000Z
字数 11188
阅读 1424
排序算法总结
目录
比较排序
- 冒泡排序
- 普通冒泡排序
- 鸡尾酒排序
- 插入排序
- 直接插入排序
- 二分插入排序
- 希尔排序
- 快速排序
- 选择排序
- “菜鸟”排序
- 简单选择排序
- 堆排序
- 归并排序
非比较排序
- 计数排序
- 基数排序
- 桶排序
前言:
通常所说的排序算法往往指的是内部排序算法,即数据记录在内存中进行排序。
排序算法大体可分为两种:
一种是比较排序,时间复杂度O(nlogn) ~ O(n^2),主要有:冒泡排序,选择排序,插入排序,归并排序,堆排序,快速排序等。
另一种是非比较排序,时间复杂度可以达到O(n),主要有:计数排序,基数排序,桶排序等。
关于算法的稳定性:
排序算法稳定性的简单形式化定义为:如果Ai = Aj,排序前Ai在Aj之前,排序后Ai还在Aj之前,则称这种排序算法是稳定的。通俗地讲就是保证排序前后两个相等的数的相对顺序不变。
对于不稳定的排序算法,只要举出一个实例,即可说明它的不稳定性;而对于稳定的排序算法,必须对算法进行分析从而得到稳定的特性。需要注意的是,排序算法是否为稳定的是由具体算法决定的,不稳定的算法在某种条件下可以变为稳定的算法,而稳定的算法在某种条件下也可以变为不稳定的算法。
例如,对于冒泡排序,原本是稳定的排序算法,如果将记录交换的条件改成A[i] >= A[i + 1],则两个相等的记录就会交换位置,从而变成不稳定的排序算法。
其次,说一下排序算法稳定性的好处。排序算法如果是稳定的,那么从一个键上排序,然后再从另一个键上排序,前一个键排序的结果可以为后一个键排序所用。基数排序就是这样,先按低位排序,逐次按高位排序,低位排序后元素的顺序在高位也相同时是不会改变的。
| 排序算法 | 平均情况 | 最好情况 | 最差情况 | 辅助空间 | 稳定性 | 备注 |
|---|---|---|---|---|---|---|
| 冒泡排序 | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 | |
| 快速排序 | O(nlogn) | O(nlogn) | O(n^2) | O(nlogn)~O(n)) | 不稳定 | |
| 直接插入排序 | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 | |
| 希尔排序 | O(nlogn)~O(n^2) | O(n^1.3) | O(n^2) | O(1) | 不稳定 | |
| 直接选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 | |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 | |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 | |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(n+k) | 稳定 | |
| 基数排序 | O(N*M) | O(N*M) | O(N*M) | O(M) | 稳定 | M为数据位数,N为数据个数 |
| 桶排序 |
各种排序算法适合在哪样的环境下使用???
一. 比较排序
1.冒泡排序
1.1 普通冒泡排序
过程如下:
- 比较相邻的元素,如果前一个比后一个大,就把它们两个调换位置。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较

public class BoobleSort {public static void sort(int[] nums){for(int i = 0; i < nums.length - 1; i++){for(int j = 0; j < nums.length - 1 - i; j++){if(nums[j] > nums[j + 1]){SortUtils.swap(nums, j, j + 1);}}}}}
1.2 鸡尾酒排序
鸡尾酒排序,也叫定向冒泡排序,是冒泡排序的一种改进。此算法与冒泡排序的不同处在于从低到高然后从高到低,而冒泡排序则仅从低到高去比较序列里的每个元素。他可以得到比冒泡排序稍微好一点的效能。
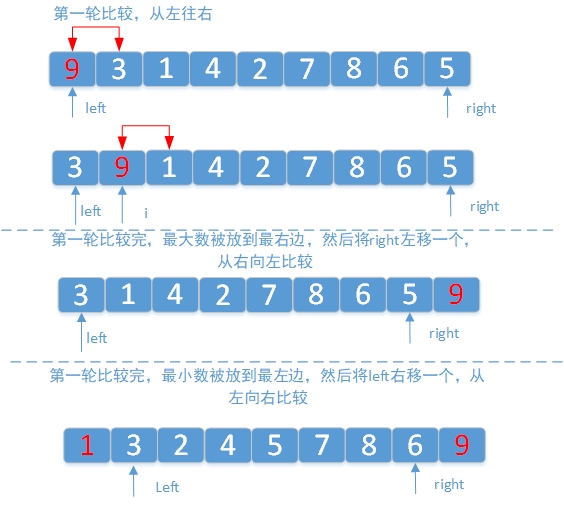
public class CocktailSort {public static void sort(int[] nums){int left = 0, right = nums.length - 1;while(left < right){for(int i = left; i < right; i++){if(nums[i] > nums[i + 1])SortUtils.swap(nums, i, i + 1);}right--;for(int i = right; i > left; i--){if(nums[i] < nums[i - 1])SortUtils.swap(nums, i, i - 1);}left++;}}}
2. 插入排序
2.1 直接插入排序
具体算法描述如下:
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5
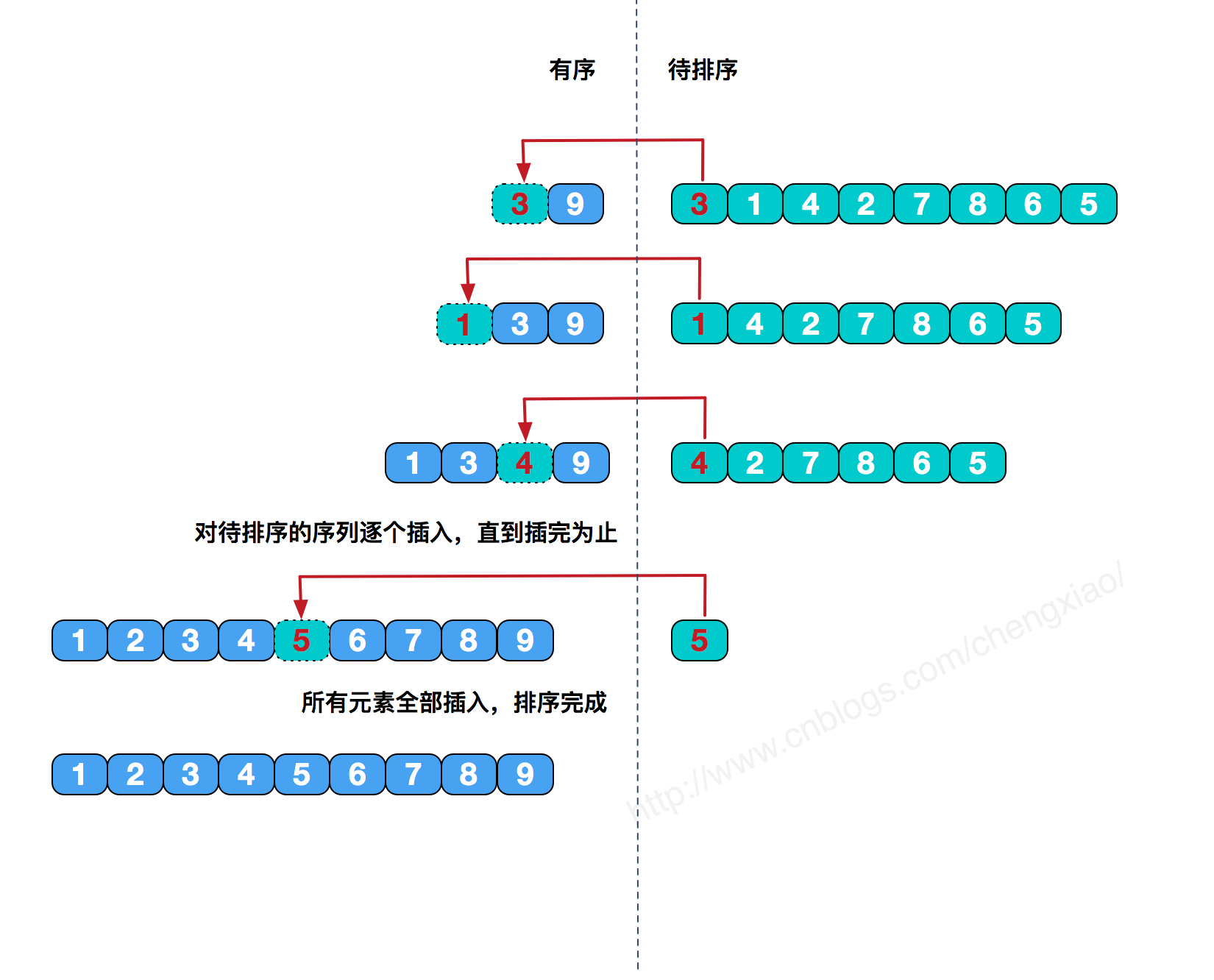
public class InsertSort {public static void sort(int[] nums){for(int i = 1; i < nums.length; i++){int get = nums[i]; //现将待排序的数取出,可以减少交换的次数int j = i - 1;while(j >= 0 && nums[j] > get){ //从后向前查找,当前数比待排序的数大,就将当前数后移,腾出位置nums[j + 1] = nums[j];j--;}nums[j + 1] = get; //当前数不比排序数大,就插入}}}
2.2 二分插入排序
对于插入排序,如果比较操作的代价比交换操作大的话,可以采用二分查找法来减少比较操作的次数,我们称为二分插入排序
public class InsertionSortDichotomy {public static void sort(int[] nums){for(int i = 1; i < nums.length; i++){int get = nums[i]; //将待排序的数取出int left = 0, right = i - 1, mid = 0;while(left <= right){ //左边已经是排好序的,可以用二分法查找mid = (left + right) / 2;if(nums[mid] > get){right = mid - 1;}else{left = mid + 1;}}for(int j = i - 1; j >= left; j--){ //移动,腾出插入的位置nums[j + 1] = nums[j];}nums[left] = get; //left的位置就是需要插入的位置}}}
2.3 希尔排序
希尔排序又叫“缩小增量排序”,是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
希尔排序的增量序列的选择与证明是个数学难题,增量取法可以参考严蔚敏的书,这里取一个递增数列,使用递增序列 1, 4, 13, 40, ...的希尔排序所需要的比较次数不会超过 N 的若干倍乘于递增序列的长度。
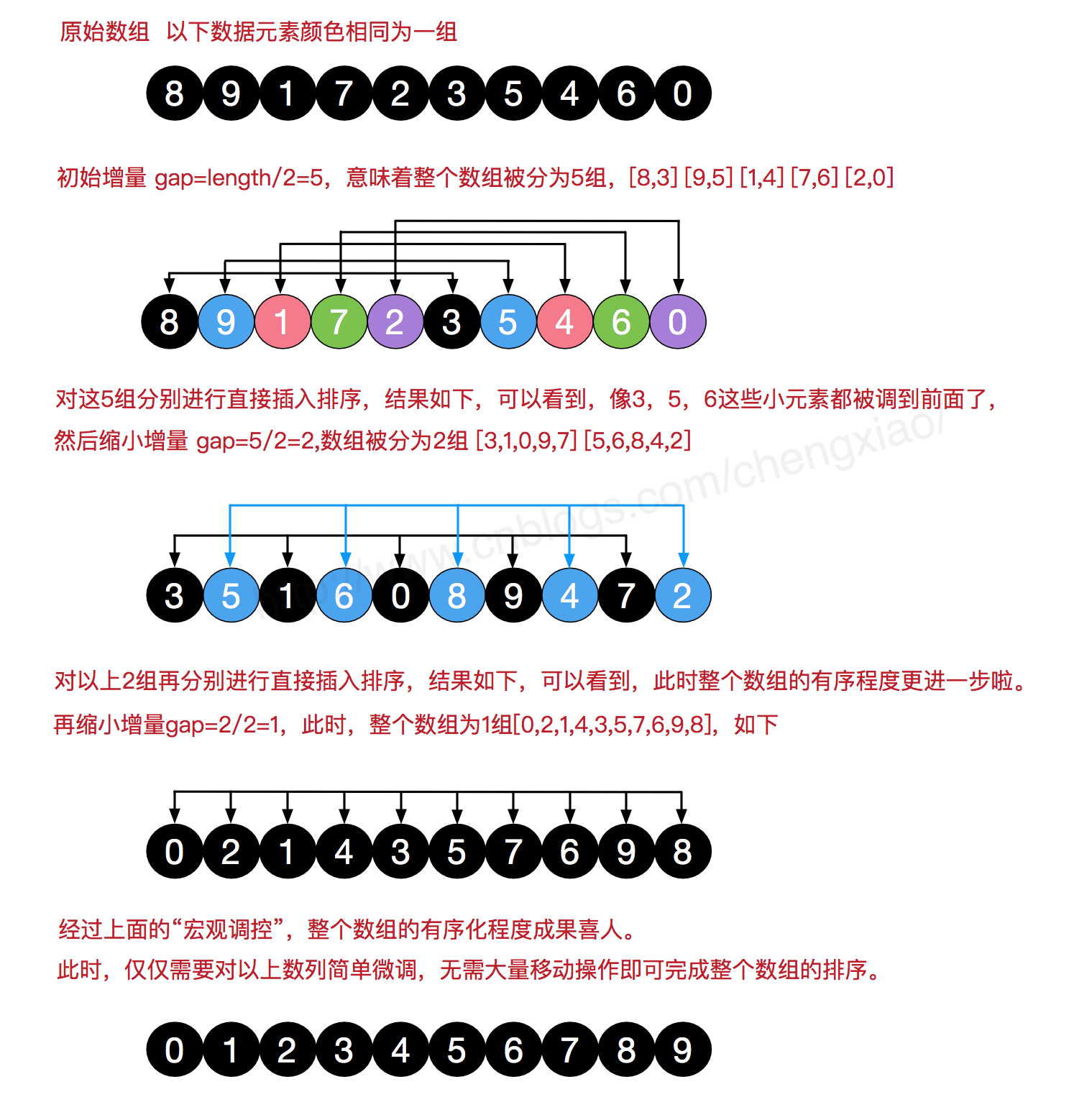
public class ShellSort {public static void sort(int[] nums){int length = nums.length;int h = 1;while(h < length / 3){h = 3 *h + 1; //增量,1,4,13,40....}while(h >= 1){for(int i = h; i < length; i++){ //插入排序int j = i - h;int get = nums[i];while(j >= 0 && nums[j] > get){nums[j + h] = nums[j];j = j - h;}nums[j + h] = get;}h = (h - 1) / 3; //缩小增量}}}
3 选择排序
3.1 “菜鸟”排序
很容易想到的一种排序方法,具体算法如下图所示。由于该算法每次都“选择”最小的元素,所以也可以看成是一种选择排序。
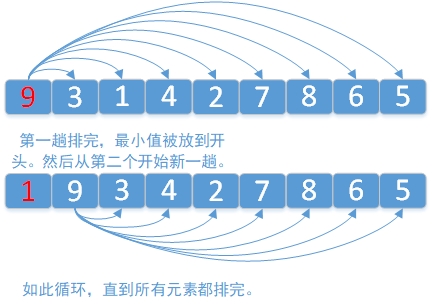
public class BirdSort {public static void sort(int[] nums){for(int i = 0; i < nums.length-1; i++){for(int j = i + 1; j < nums.length; j++){if(nums[i] > nums[j]){SortUtils.swap(nums, i, j);}}}}}
3.1 简单选择排序
选择排序也是一种简单直观的排序算法。它的工作原理很容易理解:初始时在序列中找到最小(大)元素,放到序列的起始位置作为已排序序列;然后,再从剩余未排序元素中继续寻找最小(大)元素,放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
注意选择排序与冒泡排序的区别:冒泡排序通过依次交换相邻两个顺序不合法的元素位置,从而将当前最小(大)元素放到合适的位置;而选择排序每遍历一次都记住了当前最小(大)元素的位置,最后仅需一次交换操作即可将其放到合适的位置。
选择排序可以看成是对“菜鸟”排序的一种简化,不用每次都比较。
public class SelectionSort {public static void sort(int[] nums){int min ;int temp;for(int i = 0; i < nums.length - 1; i++) {min = i; //记录最小元素的位置for (int j = i + 1; j < nums.length; j++) {if (nums[j] < nums[min]) {min = j;}}temp = nums[min];nums[min] = nums[i];nums[i] = temp;}}}
3.2 堆排序
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:
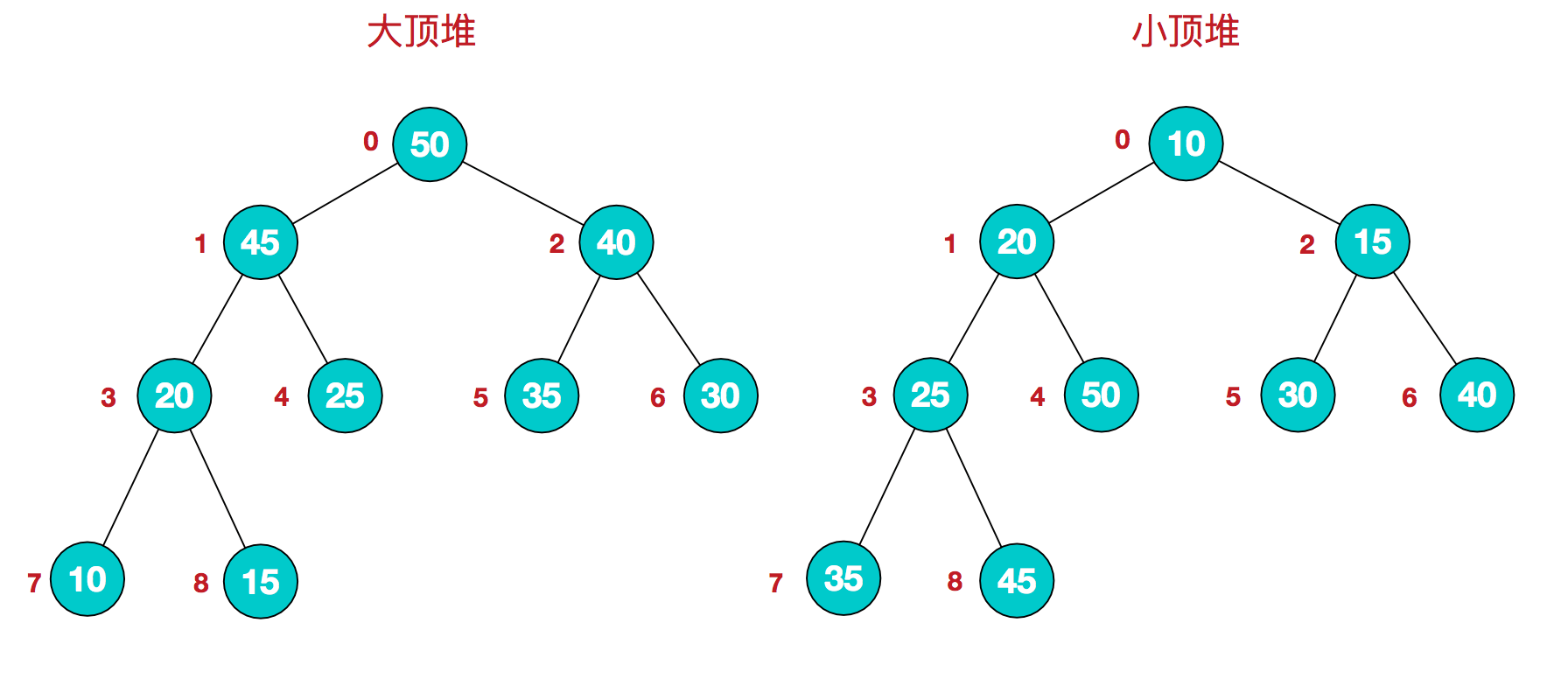
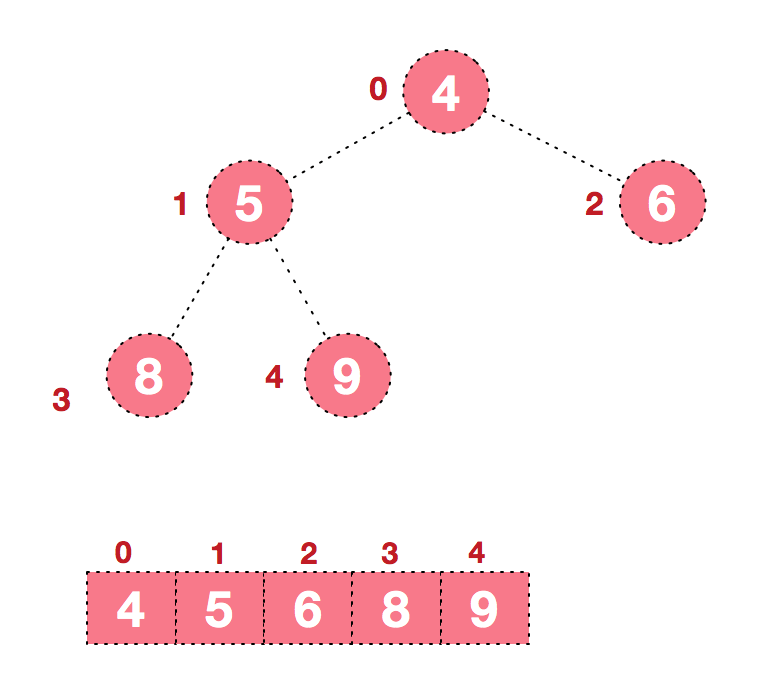
同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子

该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
注意:大顶堆和小顶堆对兄弟节点的大小关系没有要求。
堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了
- 步骤一 构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
a.假设给定无序序列结构如下
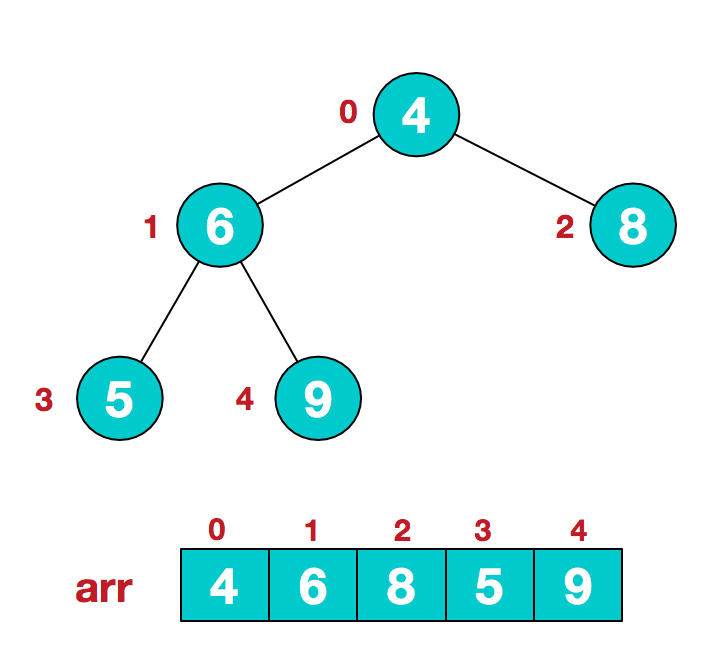
b.此时我们从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,也就是下面的6结点),从左至右,从下至上进行调整。
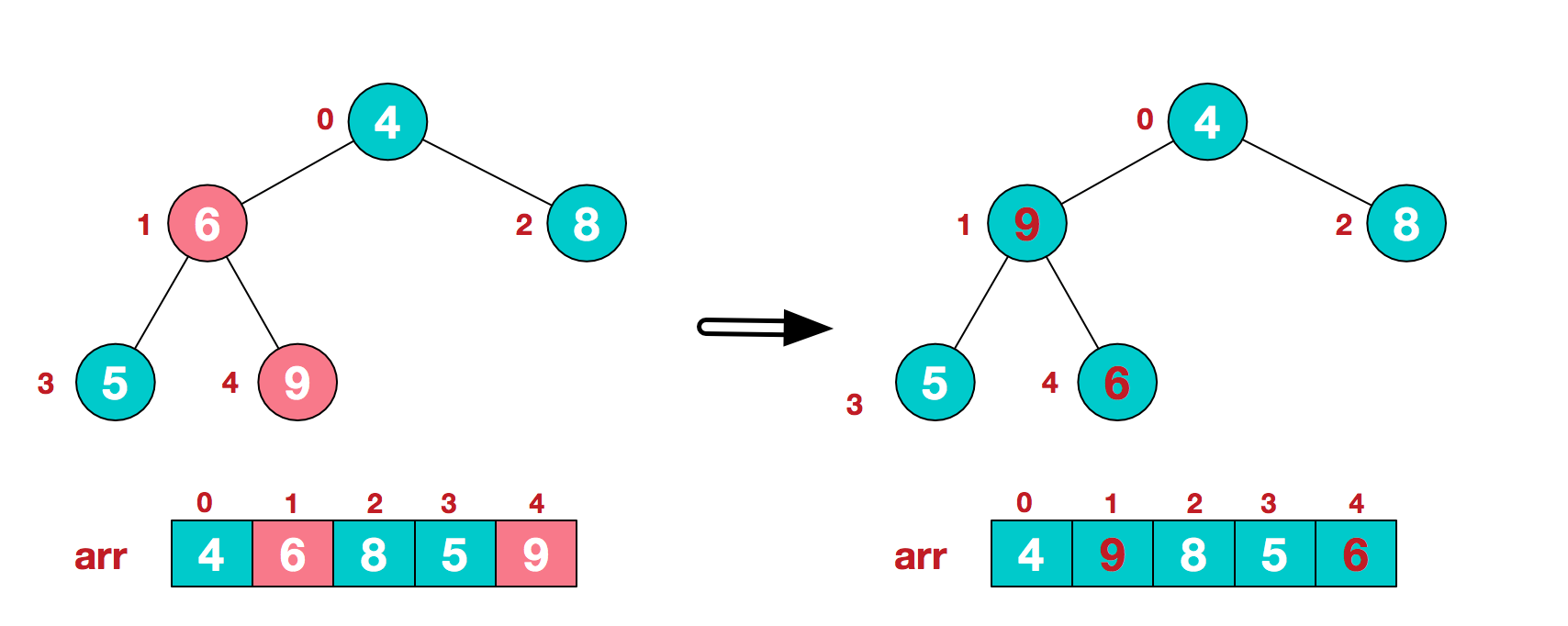
c.找到第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换。
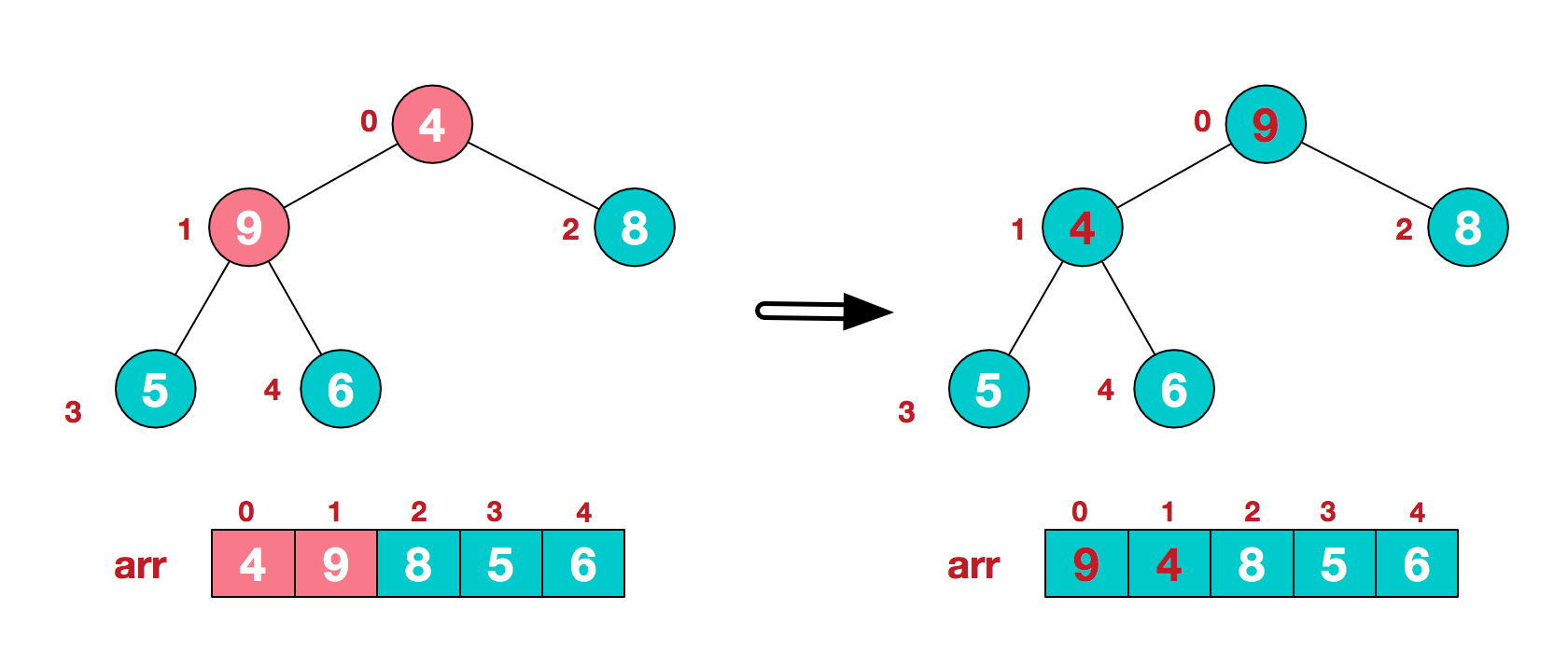
d.这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。
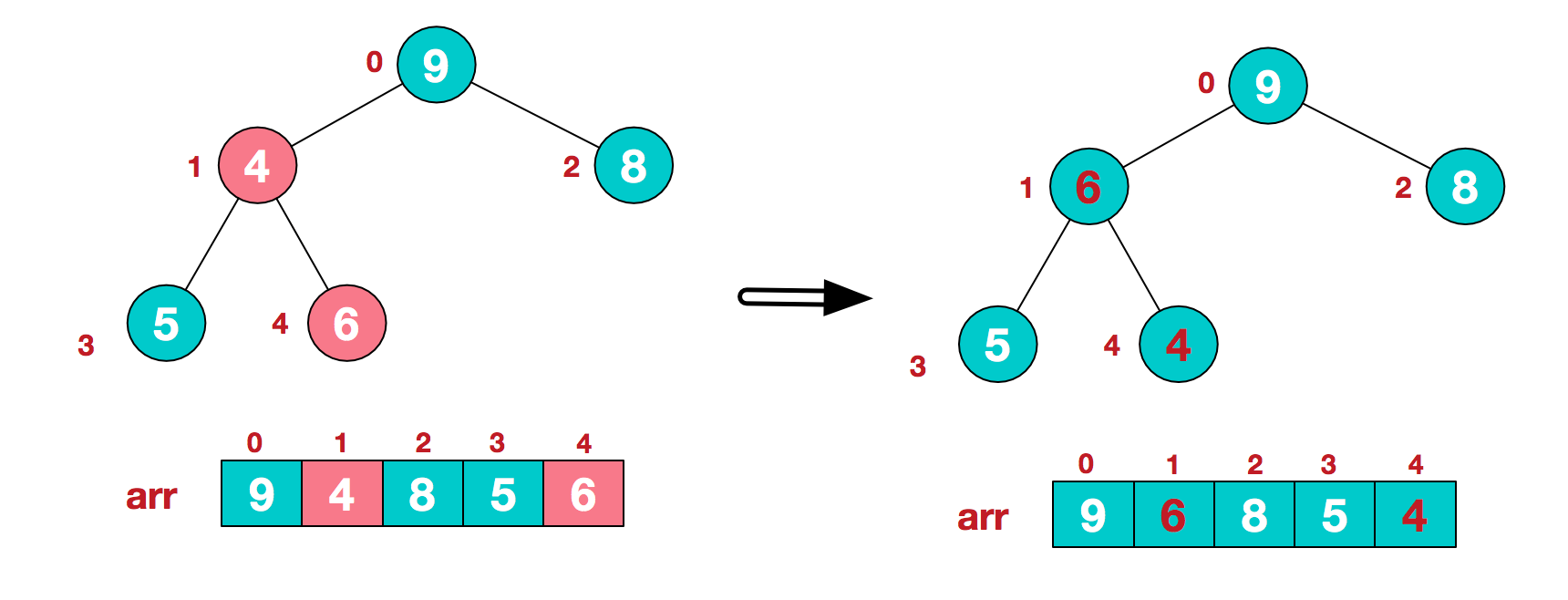
e.此时,我们就将一个无需序列构造成了一个大顶堆。
- 步骤二 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
a.将堆顶元素9和末尾元素4进行交换
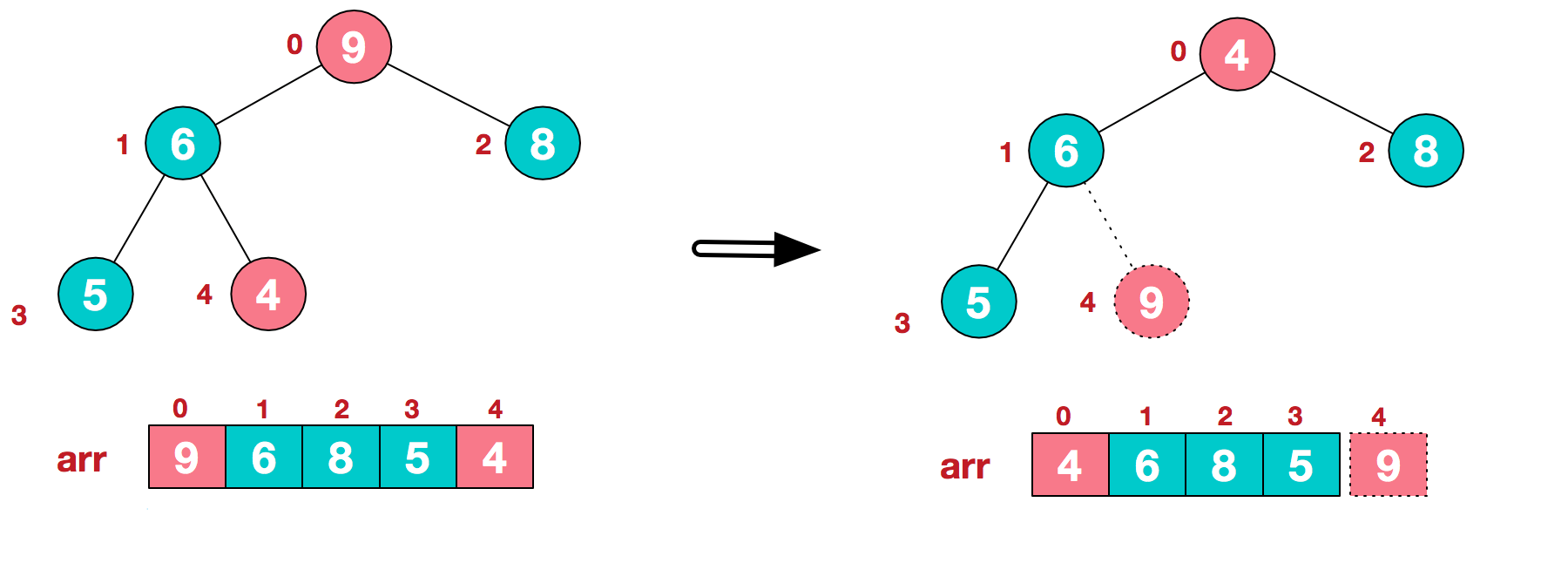
b.重新调整结构,使其继续满足堆定义
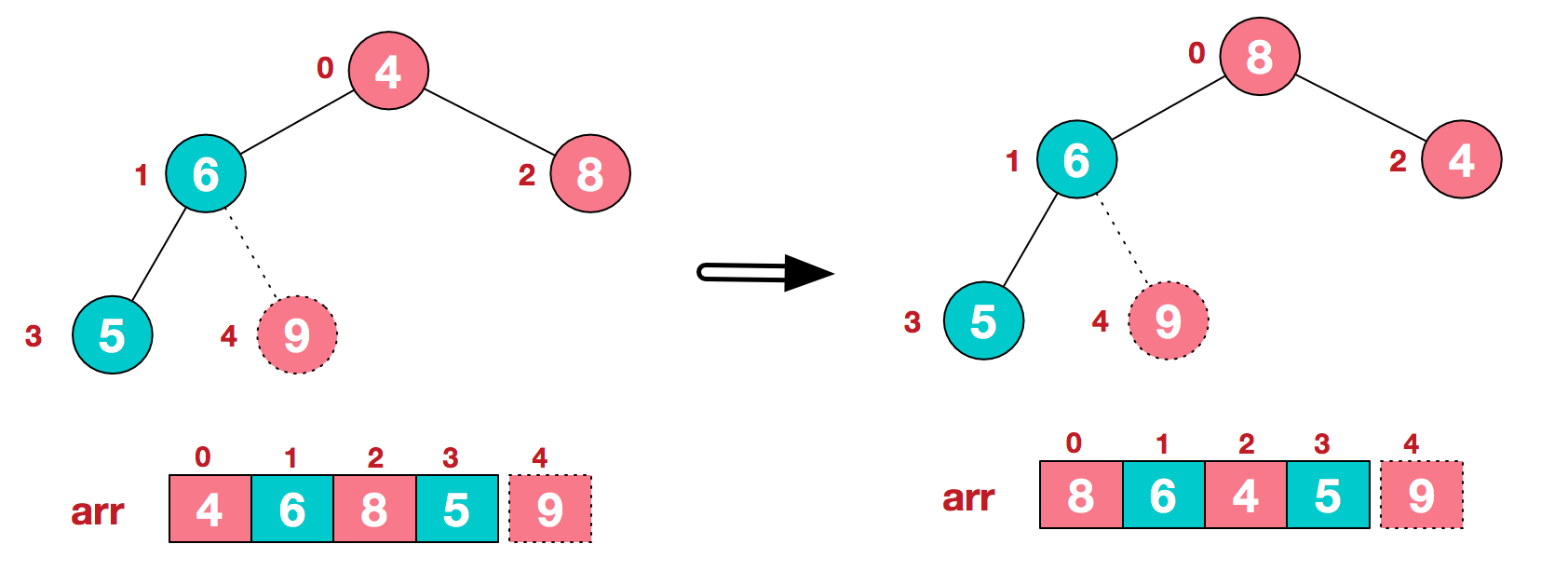
c.再将堆顶元素8与末尾元素5进行交换,得到第二大元素8.
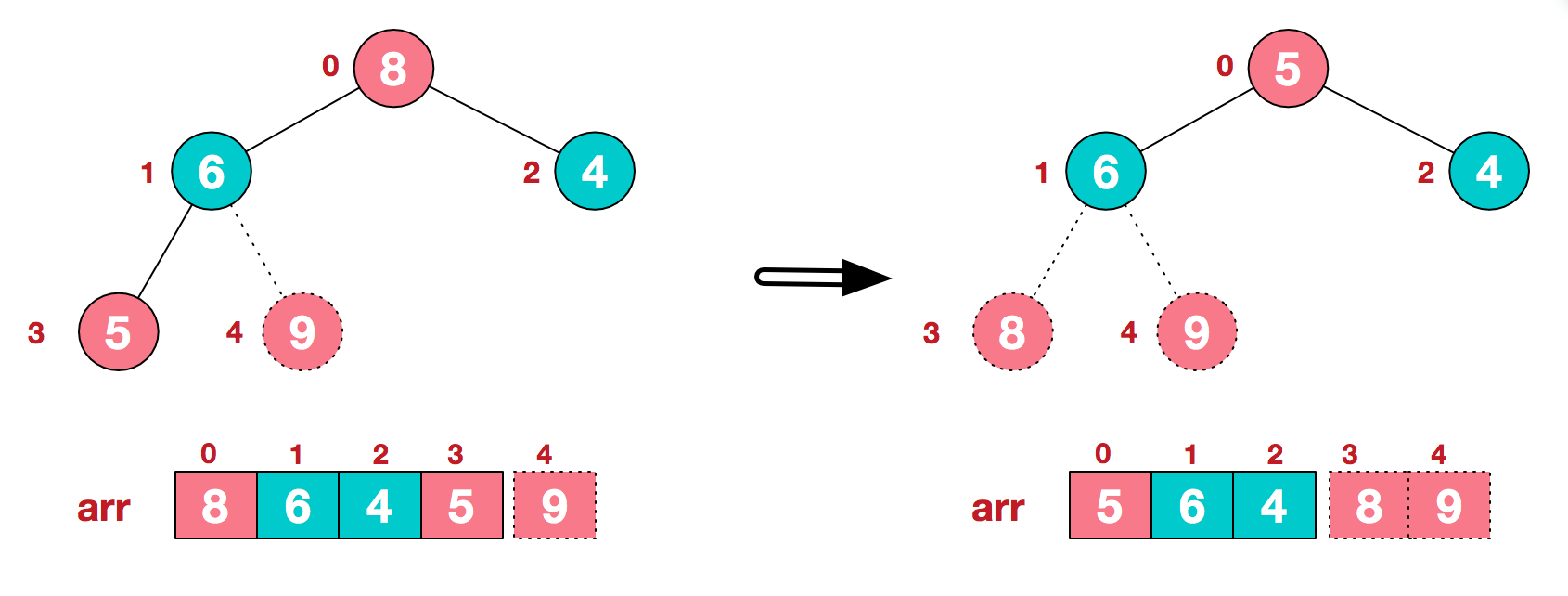
d.后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序
再简单总结下堆排序的基本思路:
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
public class HeapSort {public static void sort(int[] nums){//1.构建大顶堆for(int i = nums.length / 2 - 1; i >= 0; i--){adjustHeap(nums, i, nums.length); //从第一个非叶子结点从下至上,从右至左调整结构}//2.调整堆结构+交换堆顶元素与末尾元素for(int j = nums.length - 1; j > 0; j--){SortUtils.swap(nums, 0, j); //将堆顶元素与末尾元素进行交换adjustHeap(nums, 0, j); //重新对堆进行调整。j表示的是需要排列的数组的长度,每次讲最后一个踢出去,因为已经是最大。}}/*** 调整大顶堆。只是调整,建立在大顶堆已经构建的基础上。* @param nums:存储堆元素的数组* @param i:从第i个元素开始调整* @param length:数组的长度*/public static void adjustHeap(int[] nums, int i, int length){int temp = nums[i];for(int j = 2*i+1; j < length; j = j*2+1){ //从当前节点nums[i]的左子节点即nums[2*i+1]开始,如果当前节点的左子节点还有左子节点,继续寻找(j=j*2+1)if((j + 1) < length && nums[j] < nums[j + 1]){ //如果左子结点小于右子结点,j指向右子结点j++;}if(nums[j] > temp){ //如果子节点大于父节点,将子节点值赋给父节点(不用进行交换)nums[i] = nums[j];i = j;}}nums[i] = temp; //将当前元素放到合适的位置}}
4 归并排序
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。分阶段可以理解为就是递归拆分子序列的过程,递归深度为log2n。
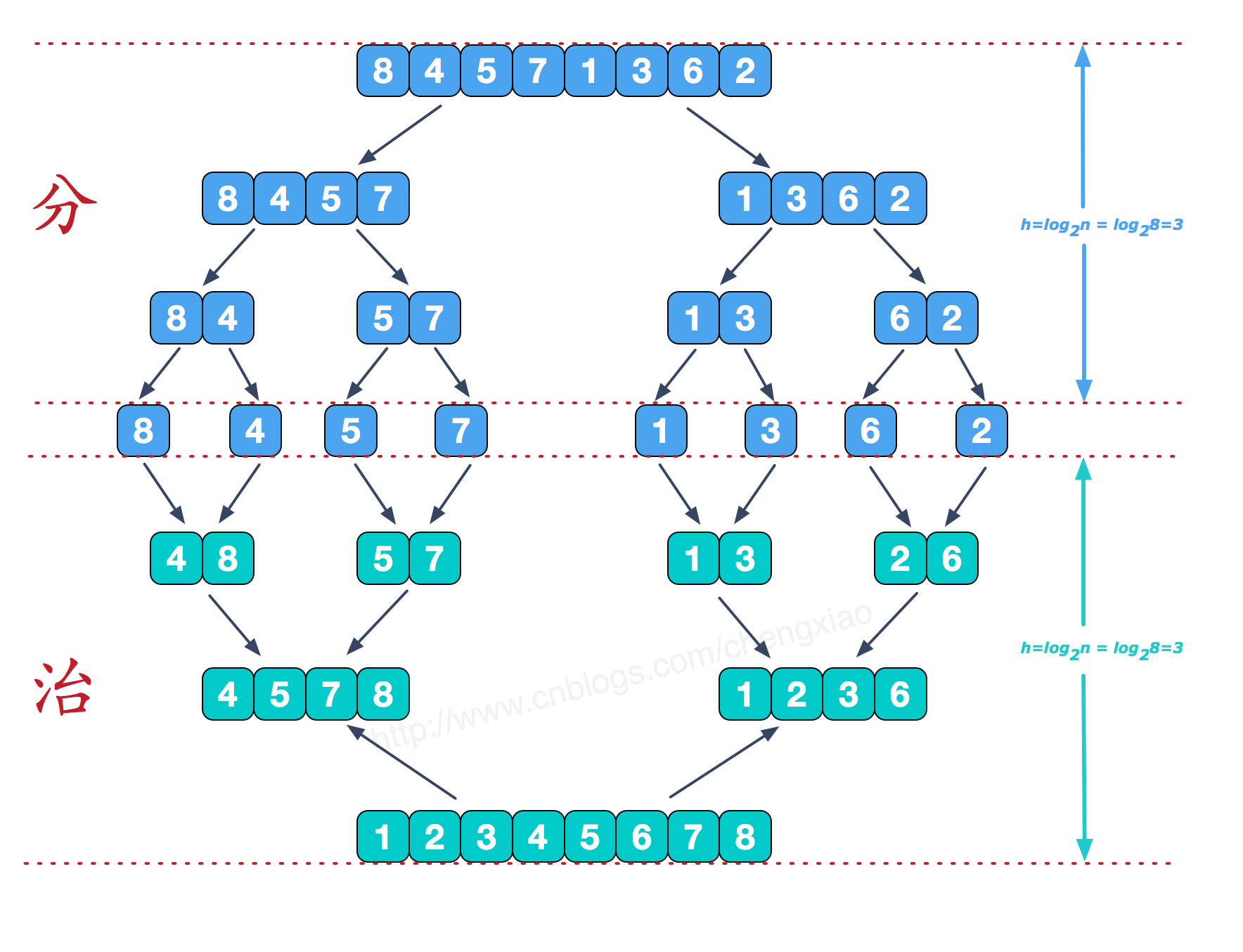
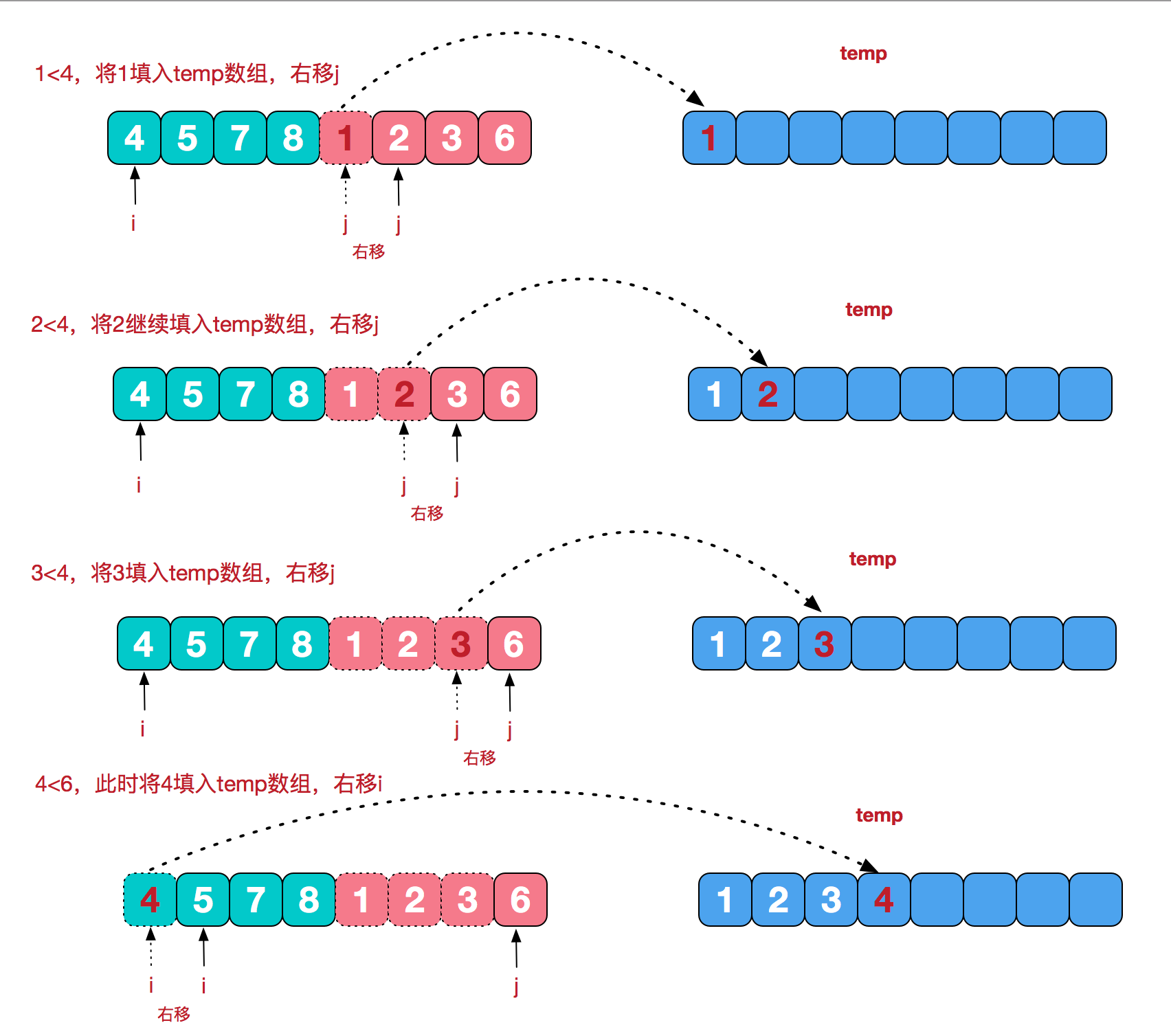
再来看看治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤。
public class MergeSort {public static void Merge(int[] A, int left, int mid, int right){//int length = A.length; //注意这里不是这么写int length = right - left + 1;int temp = 0;int[] tmp = new int[length];int i = left, j = mid + 1;while(i <= mid && j <= right){tmp[temp++] = A[i] <= A[j] ? A[i++] : A[j++]; //带等号保证排序的稳定性。}while(i <= mid){tmp[temp++] = A[i++];}while(j <= right){tmp[temp++] = A[j++];}for(int k = 0; k < length; k++){A[left++] = tmp[k]; //注意这里不是A[k]=tem[k]}}/*** 归并排序递归操作:自顶向下* @param A* @param left* @param right*/public static void sortRecursion(int[] A, int left, int right){if(left == right){return;}int mid = (left + right) / 2;sortRecursion(A, left, mid);sortRecursion(A, mid + 1, right);Merge(A, left, mid, right);}/*** 归并排序迭代操作:自下而上* @param A*/public static void sortIteration(int[] A){int left, mid, right; // 子数组索引,前一个为A[left...mid],后一个子数组为A[mid+1...right]int length = A.length;for(int i = 1; i < length; i *= 2){ // 子数组的大小i初始为1,每轮翻倍left = 0;while(left + i < length){ // 后一个子数组存在(需要归并)mid = left + i - 1;right = mid + i < length ? mid + i : length - 1; // 后一个子数组大小可能不够Merge(A, left, mid, right);left = right + 1; // 前一个子数组索引向后移动}}}}
5 快速排序
它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列
- 三数取中
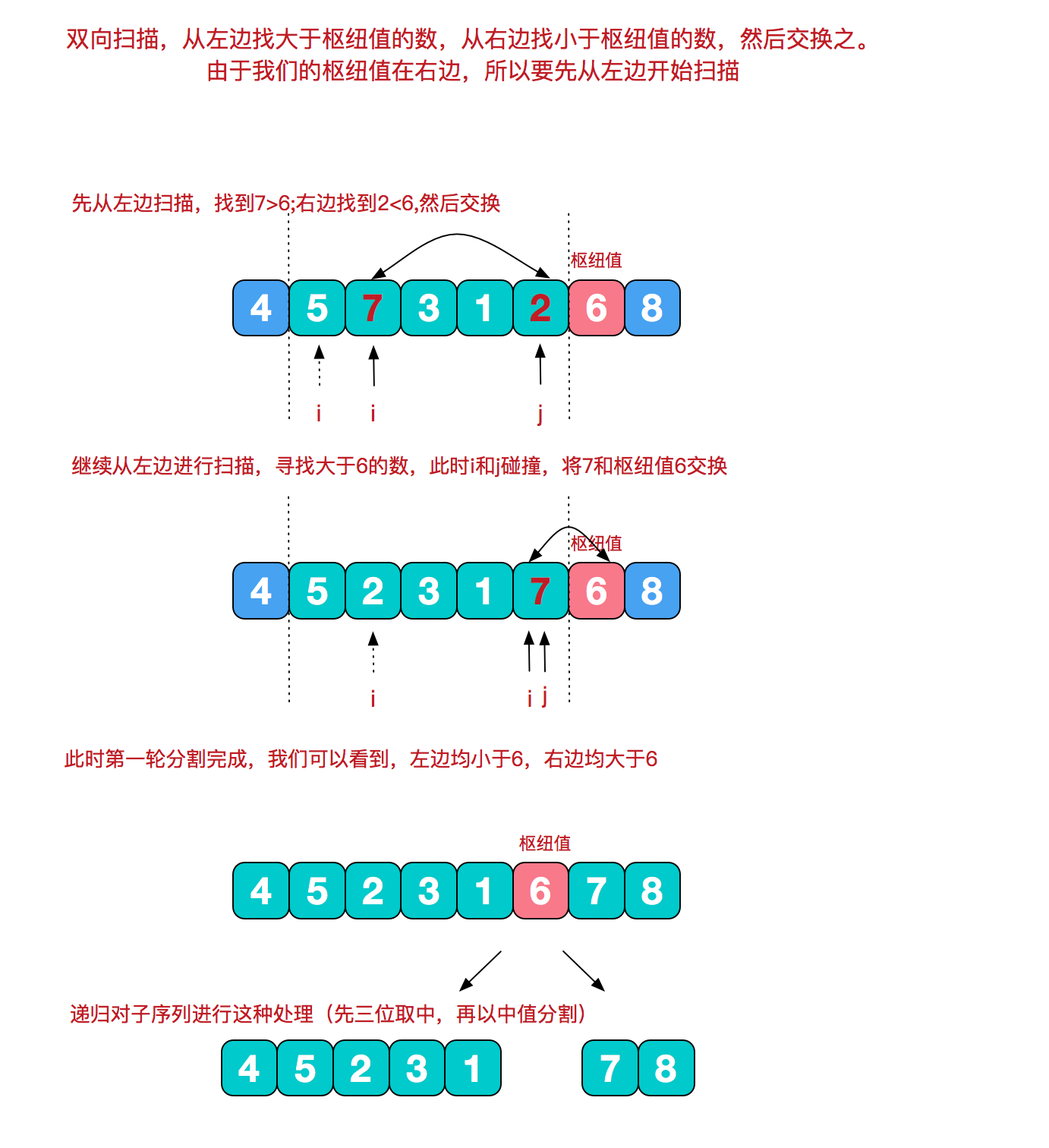
在快排的过程中,每一次我们要取一个元素作为枢纽值,以这个数字来将序列划分为两部分。在此我们采用三数取中法,也就是取左端、中间、右端三个数,然后进行排序,将中间数作为枢纽值。
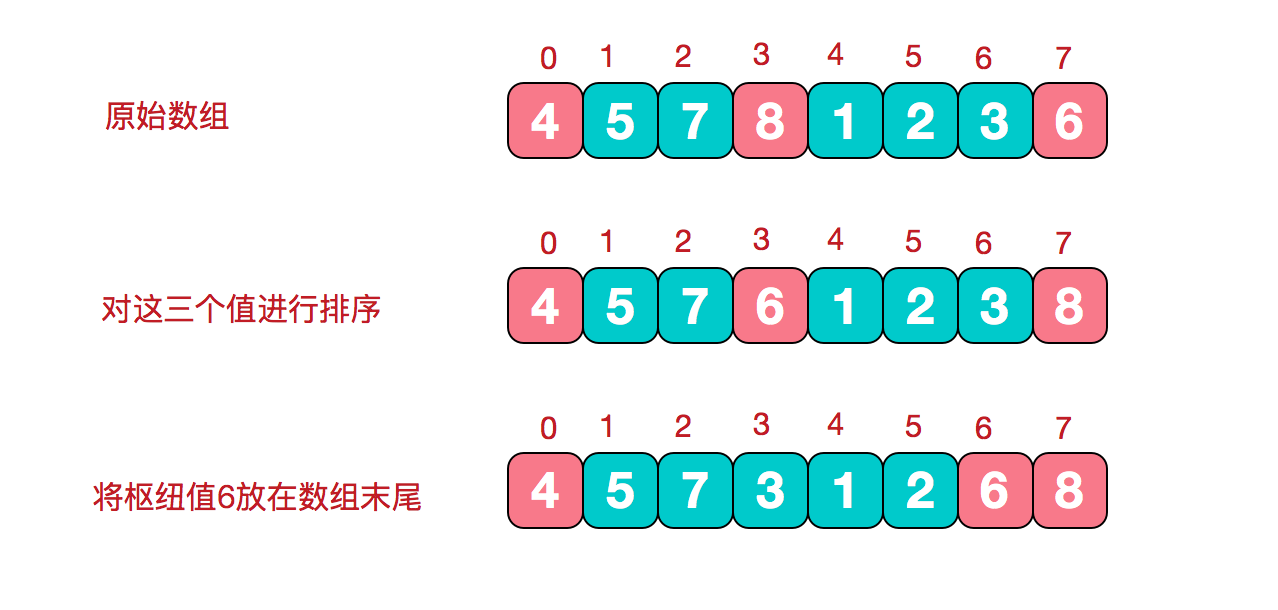
- 根据枢纽值进行分割
public class QuickSort {public static void sort(int[] arr, int left, int right) {if (left < right) {//获取枢纽值,并将其放在当前待处理序列末尾dealPivot(arr, left, right);//枢纽值被放在序列末尾int pivot = right - 1;//左指针int i = left;//右指针int j = right - 1;while (true) {while (arr[++i] < arr[pivot]) {}while (j > left && arr[--j] > arr[pivot]) {}if (i < j) {SortUtils.swap(arr, i, j);} else {break;}}if (i < right) { //将枢纽移至两块排好序的数组中间SortUtils.swap(arr, i, right - 1);}sort(arr, left, i - 1);sort(arr, i + 1, right);}}/*** 处理枢纽值** @param arr* @param left* @param right*/public static void dealPivot(int[] arr, int left, int right) {int mid = (left + right) / 2;if (arr[left] > arr[mid]) {SortUtils.swap(arr, left, mid);}if (arr[left] > arr[right]) {SortUtils.swap(arr, left, right);}if (arr[right] < arr[mid]) {SortUtils.swap(arr, right, mid);}SortUtils.swap(arr, right - 1, mid);}}
二. 非比较排序
非比较排序一般算法能做到O(logn),已经非常不错,如果我们排序的对象是纯数字,还可以做到惊人的O(n)。涉及的算法有计数排序、基数排序、桶排序,它们被归类为非比较排序。
非比较排序只要确定每个元素之前的已有的元素个数即可,遍历一次就能求解。算法时间复杂度O(n)。
非比较排序时间复杂度低,但由于非比较排序需要占用空间来确定唯一位置。所以对数据规模和数据分布有一定的要求。
1. 计数排序
计数排序的思想如下:给定待排序的数组A,首先统计A中各个元素出现的次数,将结果计入数组C中,形式为C[A[i]],这样,数组C的下标就是数组A中元素的值,数组C的值就是数组A中各个元素出现的次数,即数组C中存放的是数组A中的每个元素及其对应的出现次数。而且由于数组的下标是由小到大的,所以数组A中的值在数组C中已经是被排好序的。然后,将数组C“展开”就可以得到数组A排序后的结果,如下图所示。
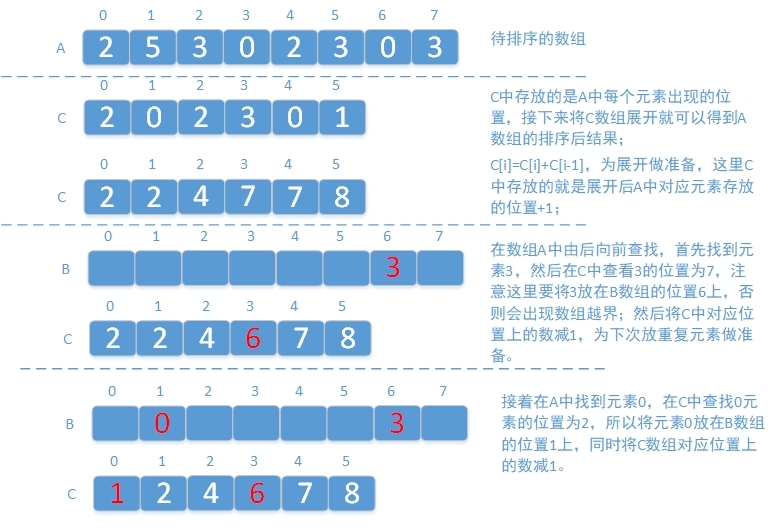
总结一下基数排序的过程;
- 统计数组
A中每个值A[i]出现的次数,存入C[A[i]]- 从前向后,使数组
C中的每个值等于其与前一项相加,这样数组C[A[i]]就变成了代表数组A中小于等于A[i]的元素个数- 反向填充目标数组
B:将数组元素A[i]放在数组B的第C[A[i]]个位置(下标为C[A[i]] - 1),每放一个元素就将C[A[i]]递减
缺点:因为构造C数组时,使用的下标为A中的元素值,所以如果A中有一个很大的元素,则构造出来的C数组势必非常大,所以,计数排序适合范围比较小的数的排序。
public class CountSort {public static int[] sort(int[] A){int[] C = new int[100]; //排序的数最大值不能超过100int[] B = new int[A.length]; //存放排序后的结果for(int i = 0; i < A.length; i++){ // 统计A中各元素个数,存入C数组C[A[i]]++;}for(int i = 1; i < C.length; i++){C[i] += C[i - 1];}for(int i = A.length - 1; i >= 0; i--){B[C[A[i]] - 1] = A[i]; //将A中该元素放到排序后数组B中指定的位置C[A[i]]--; //将C中该元素-1,方便存放下一个同样大小的元素}return B;}}
2. 基数排序
基数排序的基本思想是:将整数按位数切割成不同的数字,然后按每个位数分别比较。
具体做法是:将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
基数排序按照对位数分组的顺序的不同,可以分为LSD(Least significant digit)基数排序和MSD(Most significant digit)基数排序。
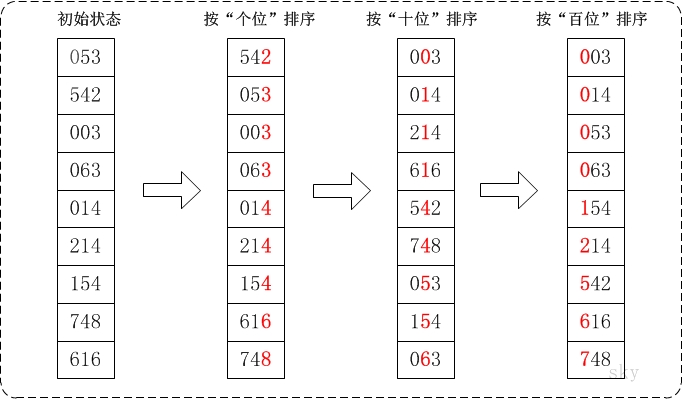
LSD基数排序,是按照从低位到高位的顺序进行分组排序。如下图所示。MSD基数排序,是按照从高位到低位的顺序进行分组排序。
由于一个数的各位、十位、百位等数的范围是0-9,所以用刚刚的计数排序比较快,故基数排序的一种方法可以是:用计数排序分别对待排序数的各位、十位等进行排序;另外,基数排序和可以用桶排序来实现。下面分别给出LSD基数排序的计数排序实现和桶排序实现。MSD实现方式可以参考MSD实现。
2.1 LSD基数排序的计数排序实现方式
- 首先通过get_max(a)获取数组a中的最大值。获取最大值的目的是计算出数组a的最大指数。
- 获取到数组a中的最大指数之后,再从指数1开始,根据位数对数组a中的元素进行排序。排序的时候采用了计数排序。
public class RadixSort {//多次调用基数排序对每一位进行排序public static void sort(int[] nums){int max = getMax(nums);for(int exp = 1; max / exp > 0; exp *= 10){countSort(nums, exp);}}//得到待排序数组中的最大值private static int getMax(int[] nums){int max = nums[0];for(int i = 0; i < nums.length; i++){if(max < nums[i]){max = nums[i];}}return max;}//计数排序private static void countSort(int[] A, int exp){int[] C = new int[10];int[] B = new int[A.length];for(int i = 0; i < A.length; i++){C[A[i] / exp % 10]++;}for(int i = 1; i < C.length; i++){C[i] += C[i-1];}for(int i = A.length - 1; i >= 0; i--){B[C[A[i] / exp % 10] - 1] = A[i];C[A[i] / exp % 10]--;}for(int i = 0; i < A.length; i++){A[i] = B[i];}}}
2.2 LSD基数排序的桶排序实现方式
- 首先获得数组的最大值,进而计算需要的最大指数。
- 建立10个桶,亦即10个数组.
- 遍历所有元素,取其个位数,个位数是什么就放进对应编号的数组,1放进1号桶。
- 再依次将元素从桶里最出来,覆盖原数组,或放到一个新数组。
- 按照上述过程依次去十位数、百位数,直到取完为止。
public class LSDRadisSort {public static void sort(int[] A){int max = A[0];for(int i = 1; i < A.length; i++){max = A[i] > max ? A[i] : max;}int bucketNum = 10; //桶的个数ArrayList<ArrayList<Integer>> bucketList = new ArrayList<>(bucketNum);for(int i = 0; i < bucketNum; i++){bucketList.add(new ArrayList<Integer>());}//从低位到高位依次入桶和出桶for(int exp = 1; max / exp > 0; exp *= 10){for(int i = 0; i < A.length; i++){int num = A[i] / exp % 10;bucketList.get(num).add(A[i]);}int j = 0;for(ArrayList<Integer> arr : bucketList){for(int i : arr){A[j++] = i;}arr.clear(); //记得清空,否则会有重复元素}}}}
3. 桶排序
桶排序的基本思想是:把数组 arr 划分为n个大小相同子区间(桶),每个子区间各自排序,最后合并。
1.找出待排序数组中的最大值max、最小值min
2.我们使用 动态数组ArrayList 作为桶,桶里放的元素也用 ArrayList 存储。桶的数量为(max-min)/arr.length+1
3.遍历数组 arr,计算每个元素 arr[i] 放的桶
4.每个桶各自排序
5.遍历桶数组,把排序好的元素放进输出数组
public class BucketSort {public static void sort(int[] nums){//找到最大值和最小值int max = Integer.MIN_VALUE;int min = Integer.MAX_VALUE;for(int i = 0; i < nums.length; i++){max = Math.max(max, nums[i]);min = Math.min(min, nums[i]);}//桶的个数int bucketNum = (max - min) / nums.length + 1;ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);for(int i = 0; i < bucketNum; i++){bucketArr.add(new ArrayList<Integer>());}//将待排序数组的中的数放入合适的桶中for(int i = 0; i < nums.length; i++){int num = (nums[i] - min) / nums.length;bucketArr.get(num).add(nums[i]);}//对每个桶进行排序for(int i = 0; i < bucketArr.size(); i++){Collections.sort(bucketArr.get(i));}//将排序后的结果由ArrayList返回到数组中int j = 0;for(ArrayList<Integer> arr : bucketArr){for(int i : arr){nums[j++] = i;}}}}
