数据结构中的算法

图

图的存储结构

邻接矩阵

邻接表

图的遍历

广度优先

深度优先

无向图的最小生成树

普利姆算法

算法描述

  假设有一个存储点的集合V[]，首先选取一个点进入集合内，找到与这个点相连接的点里面权值最小的放入集合中，然后每次在剩余点中再选取与集合内任意一点连接的点的边的权值最小的那个点放入集合，直到所有的点都在集合内。过程如下图所示：

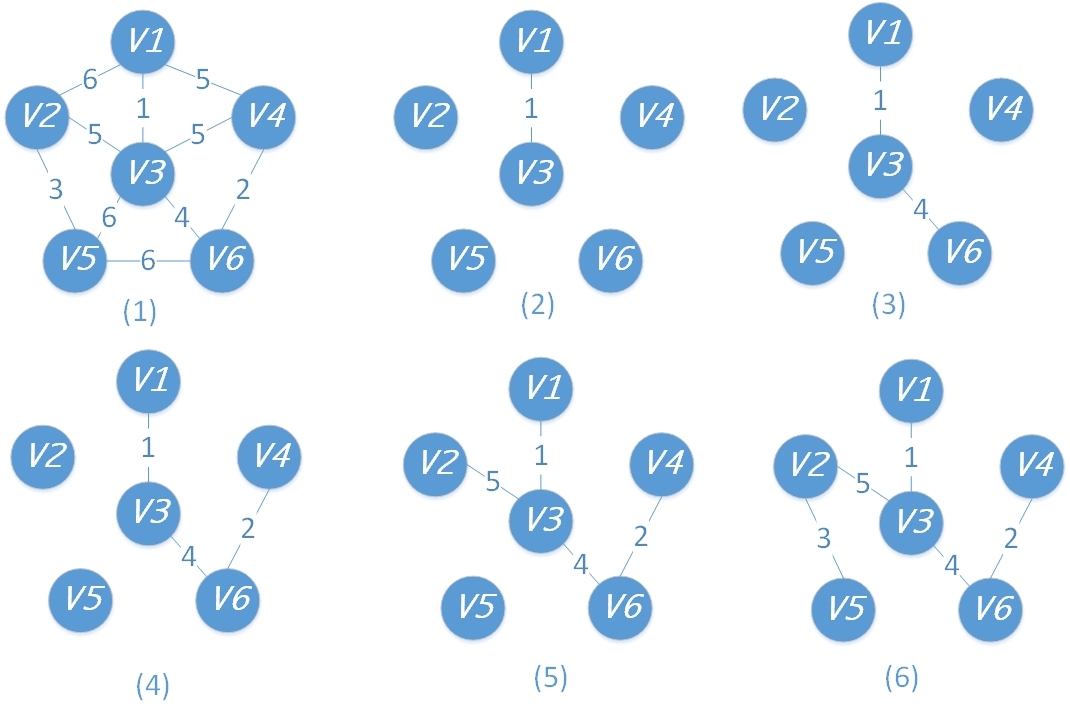
  可以看到，普利姆算法专注于“点”，每次往集合中放一个点。
  注意：如果在某次选取边的时候遇到两条边权值相等的情况，那么可以随便选一条，这样得到的图形状可能不同，但是权值的和是相等的。

算法实现

克鲁斯卡尔算法

哈希表

常用的哈希函数

直接定址法

取关键字或者关键字的某个线性函数值作为哈希地址,即：

这种散列函数也叫做自身函数.如果H(Key)的哈希地址上已经有值了,那么就往下一个位置找,知道找到H(Key)的位置没有值了就把元素放进去。

数字分析法

分析一组数据,比如一组员工的出生年月,这时我们发现出生年月的前几位数字一般都相同,因此,出现冲突的概率就会很大,但是我们发现年月日的后几位表示月份和具体日期的数字差别很大,如果利用后面的几位数字来构造散列地址,则冲突的几率则会明显降低.因此数字分析法就是找出数字的规律,尽可能利用这些数据来构造冲突几率较低的散列地址。

平方取中法

取关键字平方后的中间几位作为散列地址.一个数的平方值的中间几位和数的每一位都有关。因此，有平方取中法得到的哈希地址同关键字的每一位都有关，是的哈希地址具有较好的分散性。该方法适用于关键字中的每一位取值都不够分散或者较分散的位数小于哈希地址所需要的位数的情况。

折叠法

折叠法即将关键字分割成位数相同的几部分,最后一部分位数可以不同,然后取这几部分的叠加和(注意:叠加和时去除进位)作为散列地址。数位叠加可以有移位叠加和间界叠加两种方法。移位叠加是将分割后的每一部分的最低位对齐,然后相加;间界叠加是从一端向另一端沿分割界来回折叠,然后对齐相加。

随机数法

选择一个随机函数，取关键字的随机函数值作为它的哈希地址，即H(key)=random(key)。通常用于关键字长度不同的场合。

除留余数法

取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。即H(Key)=Key MOD p,p<=m。不仅可以对关键字直接取模,也可在折叠、平方取中等运算之后取模。对p的选择很重要，一般取素数或m，若p选得不好，则很容易产生冲突。一般p取值为表的长度tableSize。

常用的处理冲突的方法

开放地址法

这个方法的基本思想是：当发生地址冲突时，按照某种方法继续探测哈希表中的其他存储单元，直到找到空位置为止。这个过程可用下式描述：

其中： H ( key ) 为关键字 key 的直接哈希地址， m 为哈希表的长度， di 为每次再探测时的地址增量。

采用这种方法时，首先计算出元素的直接哈希地址 H ( key ) ，如果该存储单元已被其他元素占用，则继续查看地址为 H ( key ) + d 2 的存储单元，如此重复直至找到某个存储单元为空时，将关键字为 key 的数据元素存放到该单元。

增量 d 可以有不同的取法，并根据其取法有不同的称呼：
（ 1 ） d i ＝ 1 ， 2 ， 3 ， …… 线性探测再散列；
（ 2 ） d i ＝ 1^2 ，－ 1^2 ， 2^2 ，－ 2^2 ， k^2， -k^2…… 二次探测再散列；
（ 3 ） d i ＝ 伪随机序列 伪随机再散列；

优缺点：
线性探测容易产生“聚集”现象。当表中的第i、i+1、i+2的位置上已经存储某些关键字，则下一次哈希地址为i、i+1、i+2、i+3的关键字都将企图填入到i+3的位置上，这种多个哈希地址不同的关键字争夺同一个后继哈希地址的现象称为“聚集”。聚集对查找效率有很大影响。

二次探测能有效避免“聚集”现象，但是不能够探测到哈希表上所有的存储单元，但是至少能够探测到一半。

例：设有哈希函数 H ( key ) = key mod 7 ，哈希表的地址空间为 0 ～ 6 ，对关键字序列（ 32 ， 13 ， 49 ， 55 ， 22 ， 38 ， 21 ）按线性探测再散列和二次探测再散列的方法分别构造哈希表。
解：线性探测再散列：
32 ％ 7 = 4 ； 13 ％ 7 = 6 ； 49 ％ 7 = 0 ；
55 ％ 7 = 6 发生冲突，下一个存储地址（ 6 ＋ 1 ）％ 7 ＝ 0 ，仍然发生冲突，再下一个存储地址：（ 6 ＋ 2 ）％ 7 ＝ 1 未发生冲突，可以存入。
22 ％ 7 ＝ 1 发生冲突，下一个存储地址是：（ 1 ＋ 1 ）％ 7 ＝ 2 未发生冲突；
38 ％ 7 ＝ 3 ；
21 ％ 7 ＝ 0 发生冲突，按照上面方法继续探测直至空间 5 ，不发生冲突，所得到的哈希表对应存储位置：
下标： 0 1 2 3 4 5 6
49 55 22 38 32 21 13

注意：对于利用开放地址法处理冲突所产生的哈希表中删除一个元素时需要谨慎，不能直接地删除，因为这样将会截断其他具有相同哈希地址的元素的查找地址（开放地址法查找时如果遇到key为空，就停止查找，所以，后面的元素查找不到），所以，通常采用设定一个特殊的标志以示该元素已被删除。

链地址法

链地址法解决冲突的做法是：如果哈希表空间为 0 ～ m - 1 ，设置一个由 m 个指针分量组成的一维数组 ST[ m ], 凡哈希地址为 i 的数据元素都插入到头指针为 ST[ i ] 的链表中。这种方法有点近似于邻接表的基本思想，且这种方法适合于冲突比较严重的情况。

再哈希法

RHi是不同的哈希函数，即在产生地址冲突时计算另一个哈希函数地址，直到冲突不再发生。这种方法不易产生“聚集”，但增加了计算的时间。

建立一个公共溢出区

设立一个溢出表，不管哈希函数得到的哈希地址是什么，一旦发生冲突，都填入溢出表。在溢出表中按照顺序查找。

哈希表的装填因子

装填因子 = （哈希表中的记录数） / （哈希表的长度）

装填因子是哈希表装满程度的标记因子。值越大，填入表中的数据元素越多，产生冲突的可能性越大。

平均查找长度

具体的公式参看《数据结构(C语言版)》P261。

例子：假设散列表的长度是13，三列函数为H(K) = k % 13，给定的关键字序列为{32， 14， 23， 01， 42， 20， 45， 27， 55， 24， 10， 53}。分别画出用线性探测法和拉链法解决冲突时构造的哈希表，并求出在等概率情况下，这两种方法的查找成功和查找不成功的平均查找长度。

(1)线性探测再散列
使用线性探测再散列处理冲突，得到的哈希表如下：

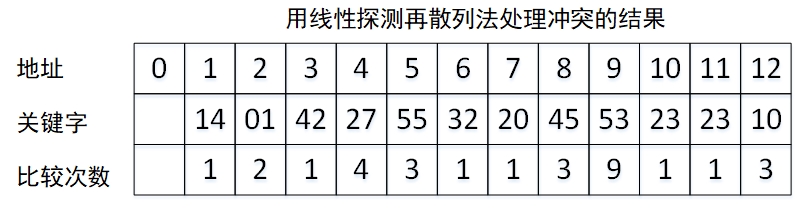
查找成功时的查找次数等于插入元素时的比较次数,查找成功的平均查找长度为：
ASL = （1+2+1+4+3+1+1+3+9+1+1+3)/12 = 2.5

计算查找不成功的次数就直接找关键字到第一个地址上关键字为空的距离即可，因为查找不成功的条件只有一种：找到了一个空地址。

哈希表中地址0的关键字为空，所以只需要计算地址1~12到地址0的距离即可，分别为：12,11,10,9,8,7,6,5,4,3,2,1。所以查找不成功的平均查找次数为：
ASL = （1+2+3+4+5+6+7+8+9+10+11+12）/ 13 = 91/13

注意：查找成功时，分母为哈希表元素个数，查找不成功时，分母为哈希表长度。（此处存在疑问）

(2)链地址法
用链地址法解决冲突得到的哈希表如下：

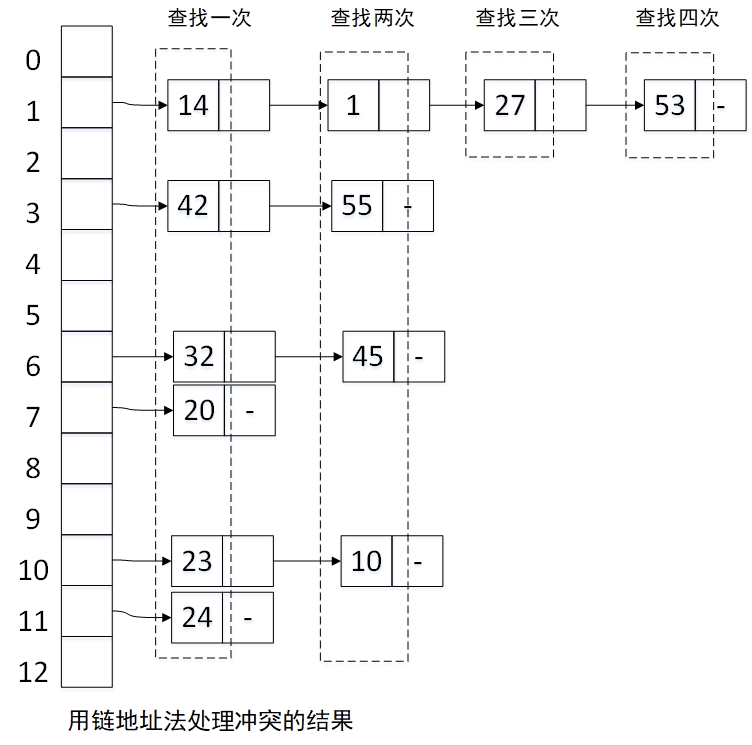
查找成功时的平均查找长度：
ASL = (1*6+2*4+3*1+4*1)/12 = 7/4

查找不成功时的平均查找长度：
ASL = (4+2+2+1+2+1)/13 = 12/13

参考：
开放地址法与链表法的优缺点及其实现
哈希表——线性探测法、链地址法、查找成功、查找不成功的平均长度
解决哈希表的冲突-开放地址法和链地址法
哈希表等概率情况下查找成功和查找不成功的平均查找长度的计算

树

二叉树(Binary Tree)
平衡二叉树(又称AVL树)
二叉搜索树(不具备平衡性)
红黑树(平衡的二叉查找树)
B树(B-Tree，多路搜索树)
B+/B-树(B树的扩展)

B+和B-的不同

• 一棵B+树中，拥有n个关键字的节点一定有n个子树；而B-树没有这么严格的规定，一棵m阶的B-树拥有的子树个数为:m/2~m个
• B+树中的信息所有值的信息全都包含在叶子节点中，非叶子节点只有关键字；