4.1 - 5.1 知识点概览

高等工程数学 讲义 2024AU

---

---

第四章 矩阵分解及其应用

---

4.1 矩阵的三角分解

方阵 $\boldsymbol{A}$ 的 三角分解（LR分解， Doolittle分解，LU分解）

$$\boldsymbol{A}=\boldsymbol{LR},$$

其中

$$\boldsymbol{L}=\left[\begin{array}{cccc}{1} \\ {l_{21}} & {1} \\ {\vdots} & {\vdots} & {\ddots} & {} \\ {l_{n 1}} & {l_{n 2}} & {\cdots} & {1}\end{array}\right], \quad \boldsymbol{R}=\left[\begin{array}{cccc}{r_{11}} & {r_{12}} & {\cdots} & {r_{1 n}} \\ & {r_{22}} & {\cdots} & {r_{2 n}} \\ & & {\ddots} & {\vdots} \\ & & & {r_{n n}}\end{array}\right].$$

---

三角分解的应用与推广

• 三角分解的本质是解线性方程组的 Gauss 消元法.
• 任何可逆的方阵都可以进行 LR 分解.
• 使用 Doolittle 紧凑计算格式，可以基于很少的存储空间实现快速的线性方程组求解.
• 由 LR 分解还可以衍生出方阵的 LDR 分解 以及正定矩阵的平方根分解 (Cholesky分解).

---

LDR 分解

$$\left[\begin{array}{ccc}{1} & {2} & {1} \\ {0} & {2} & {3} \\ {0} & {-6} & {0}\end{array}\right]=\boldsymbol{L D R}=\left[\begin{array}{ccc}{1} & {0} & {0} \\ {0} & {1} & {0} \\ {0} & {-3} & {1}\end{array}\right]\left[\begin{array}{ccc}1 \\ & 2 \\ && 9\end{array}\right]\left[\begin{array}{ccc}1&2&1\\ &1&3/2\\ &&1\end{array}\right]$$

---

正定矩阵的平方根分解

$$\left[\begin{array}{ccc}{5} & {-2} & {0} \\ {-2} & {3} & {-1} \\ {0} & {-1} & {1}\end{array}\right]=\boldsymbol{G G}^{\mathrm{T}}=\left[\begin{array}{ccc}{\sqrt{5}} & {0} & {0} \\ {-2 / \sqrt{5}} & {\sqrt{11 / 5}} & {0} \\ {0} & {-\sqrt{5 / 11}} & {\sqrt{6 / 11}}\end{array}\right]\left[\begin{array}{ccc}{\sqrt{5}} & {-2 / \sqrt{5}} & {0} \\ {0} & {\sqrt{11 / 5}} & {-\sqrt{5 / 11}} \\ {0} & {0} & {\sqrt{6 / 11}}\end{array}\right].$$

---

4.2 矩阵的正交三角分解

方阵 $\boldsymbol{A}$ 的QR分解（正交三角分解，酉三角分解）

$$\boldsymbol{A}=\boldsymbol{Q}\boldsymbol{R}$$

其中 $\boldsymbol{Q}$ 是正交/酉矩阵， $\boldsymbol{R}$ 是上三角阵.

---

QR 分解的 Schmidt 方法

• $\boldsymbol{A}=[\boldsymbol{\alpha}_1\;\boldsymbol{\alpha}_2\;\ldots\;\boldsymbol{\alpha}_n]$ 可逆.
• $\boldsymbol{Q}=[\boldsymbol{\varepsilon}_1\;\boldsymbol{\varepsilon}_2\;\ldots\;\boldsymbol{\varepsilon}_n]$ 为正交（酉）阵.
• $\boldsymbol{R}=\left[\begin{array}{cccc}\left|\boldsymbol{\beta}_{1}\right| & \langle\boldsymbol{\alpha}_{2}, {\boldsymbol{\varepsilon}_{1}\rangle} & \langle\boldsymbol{\alpha}_{3}, {\boldsymbol{\varepsilon}_{1}\rangle} & \cdots & \langle\boldsymbol{\alpha}_{n}, \boldsymbol{\varepsilon}_{1}\rangle \\ &{\left|\boldsymbol{\beta}_{2}\right|} & \langle\boldsymbol{\alpha}_{3}, {\boldsymbol{\varepsilon}_{2}\rangle} & {\cdots} & {\langle\boldsymbol{\alpha}_{n}, \boldsymbol{\varepsilon}_{2}\rangle} \\ && |\boldsymbol{\beta}_3|& \cdots & \langle\boldsymbol{\alpha}_{n}, {\boldsymbol{\varepsilon}_{3}\rangle}\\ &{} & {} & {\ddots}& \vdots\\ &{} & {} & & {\left|\boldsymbol{\beta}_{n}\right|}\end{array}\right]$ 是 $\boldsymbol{Q}$ 到 $\boldsymbol{A}$ 的过渡矩阵.

---

QR 分解的 Householder 方法

• 利用镜像变换构造 Householder 矩阵，最终将线性相关的列向量组转化为标准正交基.

QR 分解的 Givens 方法

• 利用旋转变换构造 Givens 矩阵，最终将线性相关的列向量组转化为标准正交基.

---

用 QR 分解求方阵的特征值

设 $\boldsymbol{A}\in\mathbb{C}^{n\times n}$ 的特征值满足

$$|\lambda_1|>|\lambda_2|>\ldots>|\lambda_n|>0,$$

则 $\boldsymbol{A}$ 可对角化为 $\boldsymbol{A}=\boldsymbol{P\Lambda P}^{-1}$。若 $\boldsymbol{P}^{-1}$ 存在 LU 分解 $\boldsymbol{P}^{-1}=\boldsymbol{LU}$。则当 $k\to\infty$ 时，$\boldsymbol{A}_k$ 的对角线下的元素趋于 $0$，对角线元素趋于特征值 $\lambda_1,\lambda_2,\ldots,\lambda_n$.

1. 令 $\boldsymbol{A}_1=\boldsymbol{A}$，进行 QR 分解 $\boldsymbol{A}_1=\boldsymbol{Q}_1\boldsymbol{R}_1$；
   
   • 对任意 $k\geq 1$，令 $\boldsymbol{A}_{k+1}=\boldsymbol{R}_k\boldsymbol{Q}_k$，进行 QR 分解 $\boldsymbol{A}_{k+1}=\boldsymbol{Q}_{k+1}\boldsymbol{R}_{k+1}$.
   • 持续迭代，直到 $\boldsymbol{A}_k$ 对角线下方的元素全部近似为 $0$.

---

4.3 矩阵的满秩分解

通过一系列行初等变换，将 $\boldsymbol{A}$ 化为最简形式 （Hermite 标准形）.

• $\boldsymbol{A}=\left[\begin{array}{c}{7} & {14} & {0} & {0} & {35} \\ {1} & {2} & {4} & {12} & {13} \\ {3} & {6} & {0} & {0} & {15} \\ {2} & {4} & {5} & {15} & {20}\end{array}\right] \to\ldots\to\left[\begin{array}{c}{1} & {2} & {0} & {0} & {5} \\ {0} & {0} & {1} & {3} & {2} \\ {0} & {0} & {0} & {0} & {0} \\ {0} & {0} & {0} & {0} & {0}\end{array}\right]$
• 进而 $\boldsymbol{A}=\boldsymbol{F G}=\left[\begin{array}{c}{7} & {0} \\ {1} & {4} \\ {3} & {0} \\ {2} & {5}\end{array}\right]\left[\begin{array}{c}{1} & {2} & {0} & {0} & {5} \\ {0} & {0} & {1} & {3} & {2}\end{array}\right]$，$\boldsymbol{F},\boldsymbol{G}$ 分别列、行满秩

---

满秩分解的应用

设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}, \boldsymbol{B} \in \mathbb{C}^{n \times m}$，若

$$\boldsymbol{A}\boldsymbol{B}=\boldsymbol{I}_m.$$

• 称 $\boldsymbol{A}$ 为 $\boldsymbol{B}$ 的 左逆 (Left Inverse)，记为 $\boldsymbol{B}_{\mathrm{L}}^{-1}=\boldsymbol{A}$.
  
  • 若 $\boldsymbol{F}$ 是列满秩矩阵，则 $(\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F})^{-1}\boldsymbol{F}^{\mathrm{H}}$ 是 $\boldsymbol{F}$ 的左逆.
• 称 $\boldsymbol{B}$ 为 $\boldsymbol{A}$ 的 右逆 (Right Inverse)，记为 $\boldsymbol{A}_{\mathrm{R}}^{-1}=\boldsymbol{B}$.
  
  • 若 $\boldsymbol{G}$ 是行满秩矩阵，则 $\boldsymbol{G}^{\mathrm{H}}(\boldsymbol{GG}^{\mathrm{H}})^{-1}$ 是 $\boldsymbol{G}$ 的右逆.

---

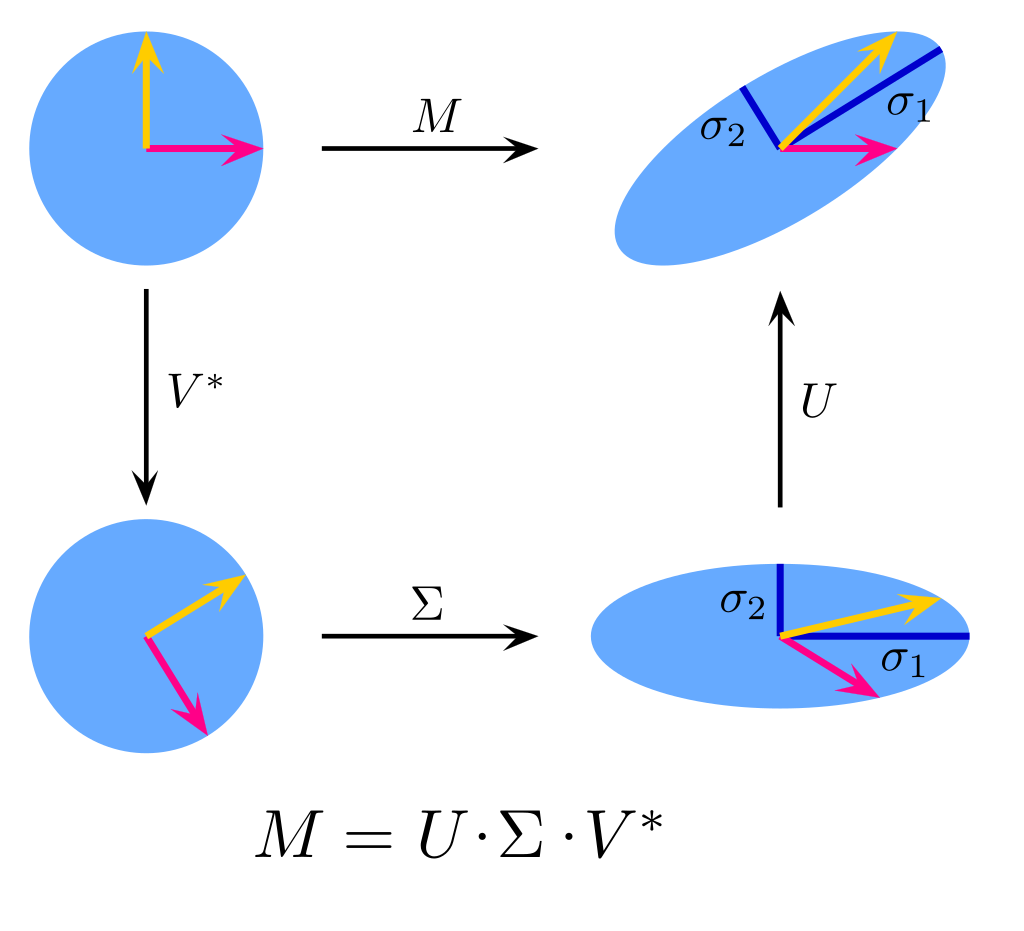
4.4 矩阵的奇异值分解（SVD）

对 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$，设 $\operatorname{rank} \boldsymbol{A}=r>0$ ，存在 $m$ 阶酉矩阵 $\boldsymbol{U}$ 和 $n$ 阶酉矩阵 $\boldsymbol{V}$ ，使得

$$\boldsymbol{U}^{\mathrm{H}} \boldsymbol{A} \boldsymbol{V}=\left[\begin{array}{ll}\boldsymbol{\Sigma} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right],$$

其中 $\boldsymbol{\Sigma}=\operatorname{diag}\left\{\sigma_{1}, \sigma_{2}, \cdots, \sigma_{r}\right\}$，$\sigma_{1} \geq \sigma_{2} \geq \cdots \geq \sigma_{r}>0$ 是 $\boldsymbol{A}$ 的正(非零)奇异值（即 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}$ 的正特征值）.

---

$$\boldsymbol{A}=\left[\begin{array}{ll}{2} & {1} \\ {0} & {2} \\ {1} & {0}\end{array}\right]=\boldsymbol{U}\left[\begin{array}{ll}\boldsymbol{\Sigma} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right] \boldsymbol{V}^{\mathrm{H}} =\left[\begin{array}{ccc}{\frac{3}{\sqrt{14}}} & {\frac{1}{\sqrt{6}}} & {\frac{2}{\sqrt{21}}} \\ {\frac{2}{\sqrt{14}}} & {-\frac{2}{\sqrt{6}}} & {-\frac{1}{\sqrt{21}}} \\ {\frac{1}{\sqrt{14}}} & {\frac{1}{\sqrt{6}}} & {-\frac{4}{\sqrt{21}}}\end{array}\right]\left[\begin{array}{cc}{\sqrt{7}} & {0} \\ {0} & {\sqrt{3}} \\ {0} & {0}\end{array}\right]\left[\begin{array}{cc}{\frac{1}{\sqrt{2}}} & {\frac{1}{\sqrt{2}}} \\ {\frac{1}{\sqrt{2}}} & {-\frac{1}{\sqrt{2}}}\end{array}\right]$$

---

SVD 的应用

1. 最小二乘问题 (Least Squares Problem)
2. 数据/图像压缩 (Data/Image Compression)
3. 潜在语义索引 (Latent Semantic Indexing)

---

第五章 矩阵的广义逆与直积

---

5.1 矩阵的广义逆及其应用

设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$ ，若存在矩阵 $\boldsymbol{G} \in \mathbb{C}^{n \times m}$ ，使得

1. $\boldsymbol{A} \boldsymbol{G} \boldsymbol{A}=\boldsymbol{A}$
2. ${\boldsymbol{G}} {\boldsymbol{A}} {\boldsymbol{G}}={\boldsymbol{G}}$
3. $(\boldsymbol{A} \boldsymbol{G})^{\mathrm{H}}=\boldsymbol{A} \boldsymbol{G}$
4. $({\boldsymbol{G}} {\boldsymbol{A}})^{\mathrm{H}}={\boldsymbol{G}} {\boldsymbol{A}}$

则称 $\boldsymbol{G}$ 为 $\boldsymbol{A}$ 的 Moore-Penrose广义逆（或 M-P广义逆，加号逆，Moore–Penrose Inverse），记为 $\boldsymbol{A}^+$ .

---

M-P 逆的计算

设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$ ，则 $\boldsymbol{A}$ 的 M-P逆存在且唯一.

1. 若 $\boldsymbol{F}$ 列满秩，则 $\bbox[lightgreen]{\boldsymbol{F}^{+}=\boldsymbol{F}_{\mathrm{L}}^{-1}=\left(\boldsymbol{F}^{\mathrm{H}} \boldsymbol{F}\right)^{-1} \boldsymbol{F}^{\mathrm{H}}}$
2. 若 $\boldsymbol{G}$ 行满秩，则 $\bbox[yellow]{\boldsymbol{G}^{+}=\boldsymbol{G}_{\mathrm{R}}^{-1}=\boldsymbol{G}^{\mathrm{H}}\left(\boldsymbol{G} \boldsymbol{G}^{\mathrm{H}}\right)^{-1}}$
3. 若 $\boldsymbol{A}$ 的满秩分解为 $\boldsymbol{A}=\bbox[lightgreen]{\boldsymbol{F}}\bbox[yellow]{\boldsymbol{G}}$, 则 $\boldsymbol{A}^{+}=\bbox[yellow]{\boldsymbol{G}^{+}}\bbox[lightgreen]{\boldsymbol{F}^{+}}=\bbox[yellow]{\boldsymbol{G}^{\mathrm{H}}\left(\boldsymbol{G} \boldsymbol{G}^{\mathrm{H}}\right)^{-1}}\bbox[lightgreen]{\left(\boldsymbol{F}^{\mathrm{H}} \boldsymbol{F}\right)^{-1} \boldsymbol{F}^{\mathrm{H}}}$
4. 设 $\boldsymbol{A}$ 的奇异值分解 $\boldsymbol{A}=\boldsymbol{U}\left[\begin{array}{ccc}{\boldsymbol{\Sigma}} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right] \boldsymbol{V}^{\mathrm{H}}$，则 $\boldsymbol{A}^{+}=\boldsymbol{V}\left[\begin{array}{ll}{\boldsymbol{\Sigma}^{-1}} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right] \boldsymbol{U}^{\mathrm{H}}$.

---

M-P 逆的应用

设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$，$\boldsymbol{x}\in\mathbb{C}^n$，$\boldsymbol{b}\in\mathbb{C}^m$，则方程组 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的全部最小二乘解为

$$\boldsymbol{x}^*=\boldsymbol{A}^{+} \boldsymbol{b}+\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{t} \quad\left(\forall \boldsymbol{t} \in \mathbb{C}^{n}\right).$$

• 若 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 是相容的，则最小二乘解就是方程的精确就.

---

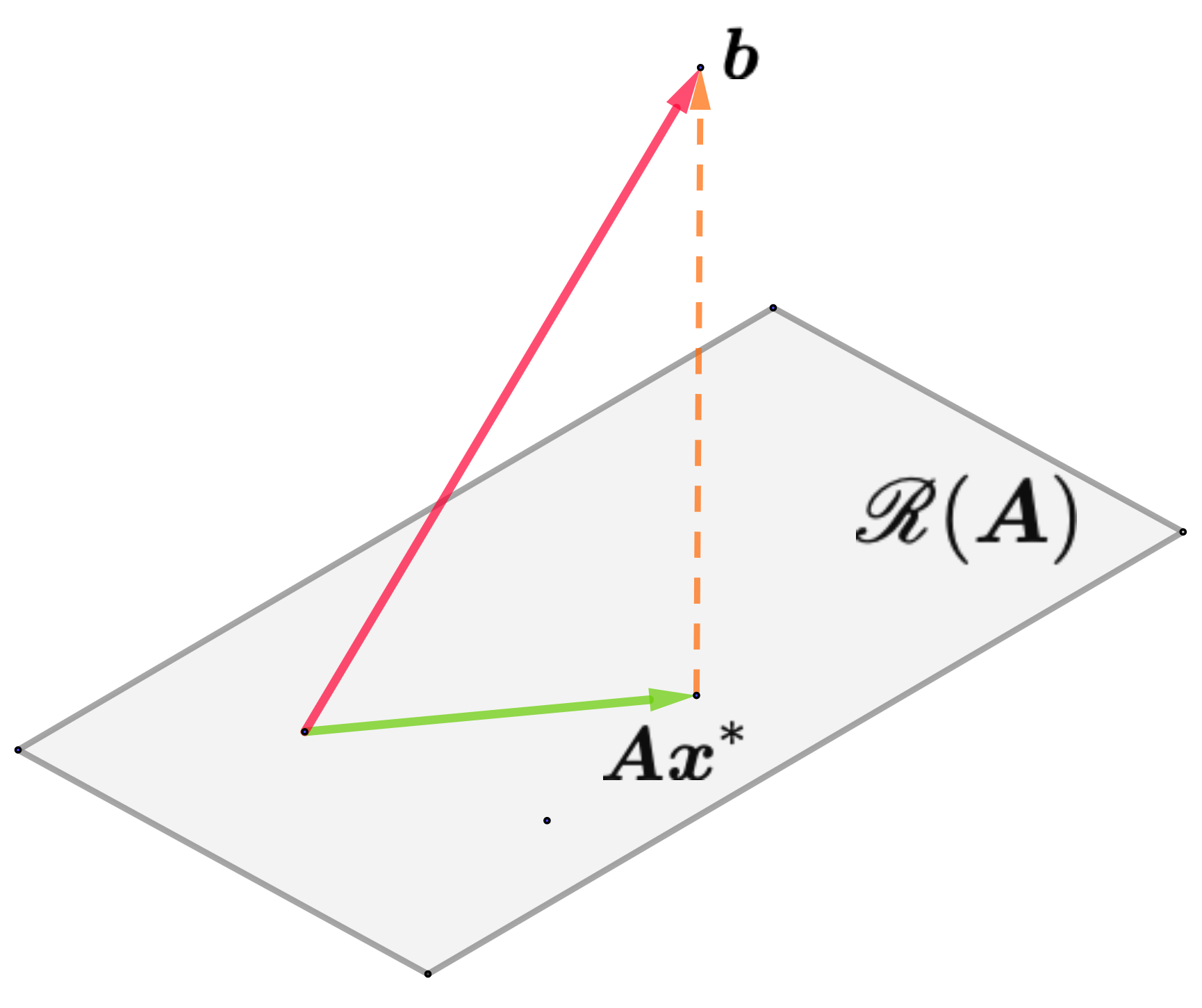
最小二乘解的几何意义

$$\left\|\boldsymbol{A} \boldsymbol{x}^{*}-\boldsymbol{b}\right\|_{2}=\min _{\boldsymbol{x} \in \mathbb{C}^{n}}\|\boldsymbol{A} \boldsymbol{x}-\boldsymbol{b}\|_{2}$$

变换 $\boldsymbol{A}$ 的值空间 $\mathscr{R}(\boldsymbol{A})$ 中与 $\boldsymbol{b}$ 距离最近的点 $\boldsymbol{A}\boldsymbol{x}^*$ 对应的原向量 $\boldsymbol{x}^*$.

• 最小二乘解中范数最小的解 $\boldsymbol{x}^{**}=\boldsymbol{A}^+\boldsymbol{b}$ 称为极小范数最小二乘解.