@ybtang21c
2025-10-19T02:21:52.000000Z
字数 19828
阅读 8499
6.1 样本与抽样分布
高等工程数学 讲义 2025AU
第二部分 数理统计与数据分析
数理统计
数理统计学的任务,统而言之,是如何获得样本(观察或试验结果)和利用样本,以对事物的某些未知方面进行分析、推断以至作出一定的决策.
-- 陈希孺,《高等数理统计学》[1]
- 试验设计(Experimental Design)、抽样调查(Sampling Survey) 研究如何收集样本.
- 统计推断(Statistical Inference) 在已有样本的情况下进行统计分析.
第二部分主要内容
抽样分布参数估计
- 矩估计
- 极大似然估计
- Bayes 估计 *
- 区间估计 *
假设检验
- 正态总体参数的假设检验
- 非参数假设检验
数据分析
- 单因子方差分析
- 主成分分析
- 多元线性回归
6.1 样本与抽样分布
6.1.1 数理统计的基本概念
- 总体 (Population):研究对象的全体.
- 数理统计中的总体通常是指:
满足某个分布的随机变量的全体. - 例如:总体 或 总体 或 总体 [2].
- 数理统计中的总体通常是指:
- 个体 (Individual): 组成总体的每一个考察对象.
- 例如:某个服从 的随机变量 .
- 随机变量 (Random Variable,简写 rv): 被研究对象的数量指标.
- 分布函数(CDF):.
- 样本 (Sample):所有被抽取的个体(随机变量)所组成的集合.
设随机变量 ,若 相互独立,且与 同分布[3],则称
为来自总体 的 简单随机样本(Simple Random Sample,简称 随机样本),称 为 样本容量(Sample Size).
- 样本的二重性 (Dualism of Sample)
- 试验前,样本是独立同分布的
随机变量. - 试验后,样本是确定的数据(
样本观测值,Sample Observation) .
- 试验前,样本是独立同分布的
例 为了考察某种器件的寿命,从一批产品中随机抽取 件产品进行了寿命试验,得到试验结果如下:
- 样本容量 .
- 二重性:
- 样本 是独立同分布的随机变量.
- 样本观测值:.
- 统计推断问题的基本构成要素:总体及其分布、样本容量、样本观测值.
样本的联合分布
设 是来自总体 的简单随机样本
- 的 联合分布(函数) (Joint CDF)
-
6.1.2 统计量及其分布
设 是来自总体 的简单随机样本,若 是 元连续函数,且不含任何未知参数,则称随机变量
为 统计量 (Statistics).
- 统计量是样本的函数.
- 统计量的分布称为 抽样分布 (Sample Distribution).
例 设 是来自总体 的简单随机样本,其中 均未知,则下列随机变量中哪些是统计量?
, , , ,
注: 尽管统计量的取值不依赖于未知参数,但是它的分布一般还是依赖于未知参数的.
常用的统计量
- 样本均值(Sample Mean)
- 样本方差(Sample Variance)
- 样本标准差(Sample Standard Deviation)
- 修正的样本方差(Modify Sample Variance)
- 样本 k 阶(原点)矩 (k-th Moment of the Sample)
- 样本 k 阶中心矩 (k-th Central Moment of the Sample)
- 样本偏度 (Sample Skewness)
- 反映样本数据相对于对称状态的偏离程度和偏离方向
- 样本峰度 (Sample Kurtosis)
- 反映总体分布密度曲线在其峰值附近的陡峭程度和尾部粗细
- 样本极小值(Minima of the Sample)
- 样本极大值(Maxima of the Sample)
- 第 k 个次序统计量(k-th Order Statistics) 表示从小到大的第 个值对应的随机变量
- 样本极差(Sample Limit Error)
- 样本中值(Sample Median)
样本均值
- 偏差 (Deviation):数据与均值之差,.
- 定理: 样本的总偏差之和为零,即 .
- 定理: 数据观测值与均值的偏差平方和最小.
- 即:在形如 的函数中, 最小.
提示: 对任意 ,
中心极限定理
定理 设 是来自某个总体的随机样本, 为样本均值.
- 若总体分布为 ,则 的
精确分布为 . - 若总体分布未知或不是正态分布,总体均值 和总体方差 均存在,则当 较大时 的
渐进分布为 .
例[4] 当样本容量 时,
- 若 ,则
- 近似服从
- 若 的密度函数为
- 近似服从
- 若 ,则
- 近似服从
样本方差与样本标准差
- 定理[5] 设总体的均值 的方差 均存在, 为来自该总体的简单随机样本,则
- ,.
- ,.
次序统计量
定理[6] 设总体 的密度函数和分布函数分别为 和 ,且 为来自 的简单随机样本,则从小到大排列的第 个次序统计量 的密度函数为
样本分位数
样本 分位数 (Quantile):
- 定理 设总体密度为 , 为其 分位数,且 在 处连续且 ,则当 时, 的渐进分布为 .
一些相关的计算公式
- 记 ,则
- 记 ,则
- 抽取两个容量分别为 的样本,样本均值分别为 ,修正的样本方差分别为
- 设总体的四阶中心矩 存在, 为总体方差,则
6.1.3 抽样分布与抽样分布定理
常用的抽样分布
- 正态分布(Normal Distribution)
- -分布
- t-分布
- F-分布
常用分布一:卡方分布
设 是来自总体 的简单随机样本,称随机变量
服从 自由度(Degree of Freedom) 为 的 -分布 (Chi-Square Distribution),记为 .
正态分布的基本性质
- 正态分布随机向量的任意线性变换仍为正态随机向量,即:正态性在线性变换之下保持不变.
- 利用线性变换可以将任何正态分布化为标准正态分布,即:若 ,则 .
- 若 ,则
卡方分布的密度函数(PDF)
- -分布是一种特殊的 -分布:
- 相当于
- 的密度函数
关于 Γ-函数[7]
-
- -函数也叫 Euler 第二积分,是
阶乘在实数与复数域上的扩展
- -函数也叫 Euler 第二积分,是
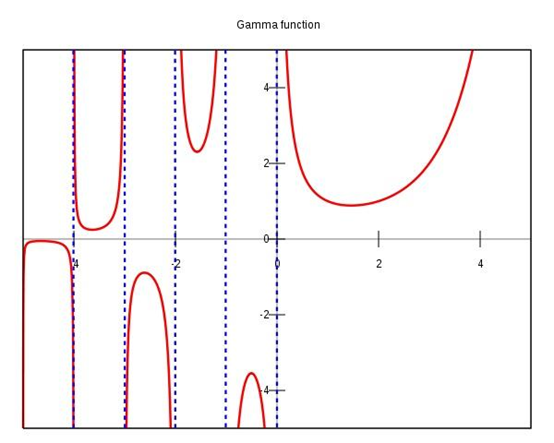
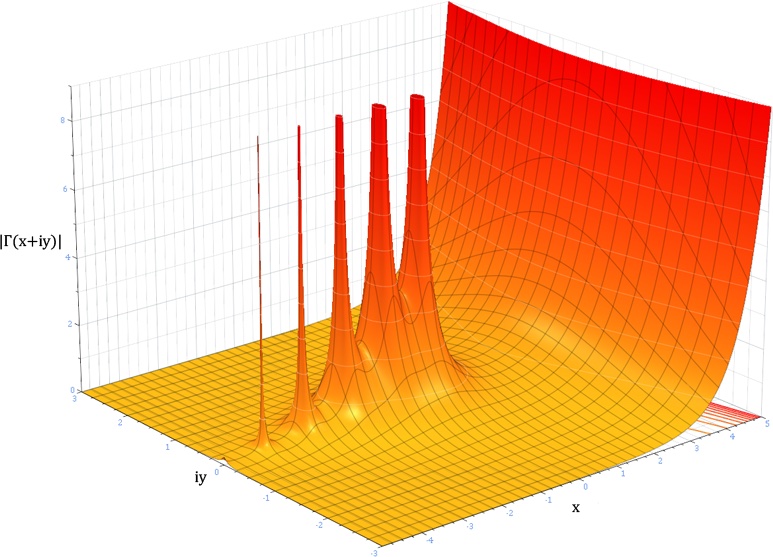
-函数在复平面上的图像
基本性质:卡方分布
- 若 ,则
- .
- .
- 若 ,且 与 相互独立,则 .
- 注意: 已知 ,,不一定能推出 .
性质2的证明:
- 设 独立同分布,服从 ,故 .
- 于是 与 同分布,记为
- 同理,存在 独立同分布,服从 ,且与 相互独立,则
- 与 相互独立,则其联合分布函数为其边缘分布函数的乘积.
- 与 相互独立,其联合分布函数为其边缘分布函数的乘积.
- 显然以上两个联合分布函数相同,故有
- 进而可得 .
例 设 相互独立,求如下统计量的分布:
提示:, .- 服从正态分布,故 .
- 同理 .
- 由 -分布的定义,
History of Chi-Square Distribution[^6]
- distribution was first described by the German statistician Friedrich Robert Helmert (1843-1917) in papers of 1875–6,where he computed the sampling distribution of the sample variance of a normal population.
- In German this was traditionally known as the Helmert'sche ("Helmertian") or "
Helmert distribution". - The distribution was independently rediscovered by the English mathematician Karl Pearson (1857-1936) in the context of goodness of fit, for which he developed his Pearson's chi-square test, published in 1900, with computed table of values published.
- The name "chi-square" ultimately derives from Pearson's shorthand for the exponent in a multivariate normal distribution with the Greek letter Chi.
- The idea of a family of "chi-square distributions", however, is not due to Pearson but arose as a further development due to Fisher in the 1920s.
抽样分布定理一:抽样分布基本定理
定理 设 是来自 的简单随机样本,则
- .
- .
- 与 (以及 ) 相互独立.
证明概要: 记 ,,于是
-
- .
- 可以验证,,且 的 阶顺序主子式大于 ,故 .
- 可以验证, ,即 为幂等阵,故 的特征值只能为 或 .
- 进而可知存在正交阵 ,使得
- 令 ,则
-
- .
-
- 注意到 的每个分量 均为相互独立的正态随机变量的线性组合,故其必服从正态分布.
- 又 .
-
- .
- 由此可知 的各分量均相互独立且服从 ,
- 进而可知 .
- 可以验证 是 与特征值 对应的单位特征向量.
- 的列向量均为 的单位特征向量,故 恰好为其最后一列,
- 于是 .
- 因为 与 相互独立,故 与 相互独立.
抽样分布基本定理的现实意义
- .
- 随着样本容量的增加, 与 的总偏差将越来越小
- 或者说:大量重复试验有助于提高均值的估计精度.
- 与 (以及 ) 相互独立.
- 样本均值和样本方差(以及修正的样本方差)之间相互独立,
- 或者说:总体均值和方差可以分别进行估计.
如何避免噪声淹没速度?
- 利用测速雷达连续测量飞机相对的径向速率,进而解算出飞机的速度
- 受电、磁、气象干扰等各种噪声影响,数据存在明显的抖动
- 在低速情况下,真实的速度往往会被噪声“淹没”
- 为了尽可能消除噪声的影响,一般需要采用“窗口平滑”的方法
常用分布二:t-分布
设 ,, 与 相互独立,则称随机变量
服从自由度为 的 t-分布,记为 .
思考:设 且相互独立, 吗?
- 错!应该是 .
t-分布的密度函数
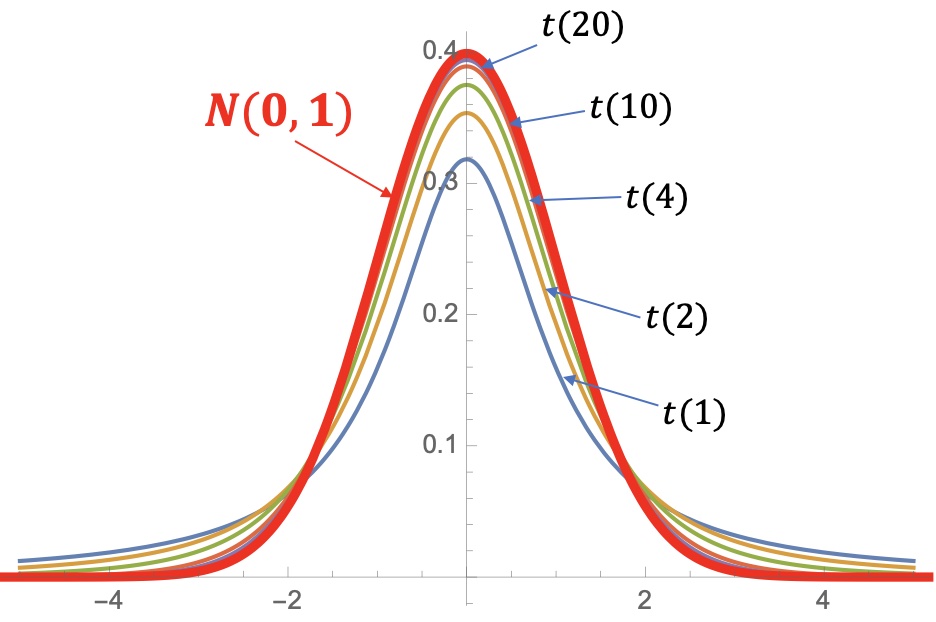
- 随着 的增大, 的概率密度越来越接近于 .
History of t-Distribution[8]
- In statistics, the t-distribution was first derived as a posterior distribution in 1876 by Helmert and Lüroth. The t-distribution also appeared in a more general form as Pearson Type IV distribution in Karl Pearson's 1895 paper.
- In the English-language literature the distribution takes its name from William Sealy Gosset (1876-1937)'s 1908 paper in Biometrika under the pseudonym "Student".
- Gosset's paper refers to the distribution as the "frequency distribution of standard deviations of samples drawn from a normal population".
- It became well known through the work of Ronald Fisher, who called the distribution "Student's distribution" and represented the test value with the letter t.
抽样分布定理二
定理 设 是来自正态总体 的简单随机样本,则
- 注意和 比较.
抽样分布定理三
定理 设 是来自正态总体 的简单随机样本, 是来自正态总体 的简单随机样本,且两组样本相互独立,则
其中 , 分别为两组样本对应的样本方差.
常用分布三:F-分布
设 ,, 相互独立,则称随机变量
服从自由度为 的 F-分布.
- 记为 .
- 显然,若 ,则 .
F-分布的密度函数
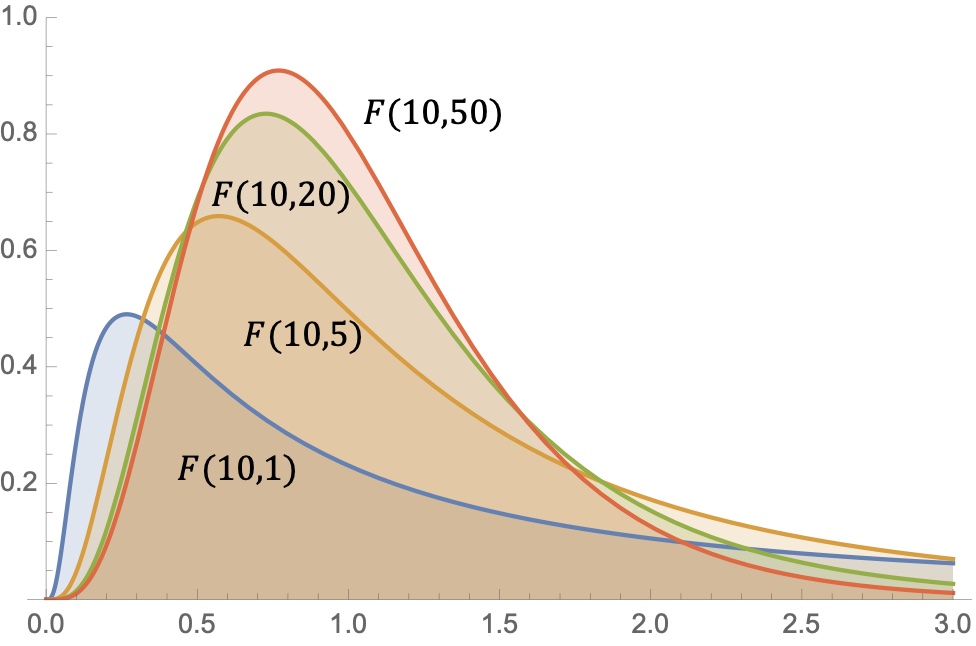
Histroy of F-Distribution[9]
- The F-distribution, also known as Snedecor's F distribution or the Fisher–Snedecor distribution (after Ronald Fisher(1890-1962) and George W. Snedecor(1881-1974))
- arises frequently as the null distribution of a test statistic, most notably in the
analysis of variance (ANOVA), e.g.,F-test.
抽样分布定理四
定理 设 是来自正态总体 的简单随机样本, 是来自正态总体 的简单随机样本,且两组样本相互独立. 分别表示两样本的样本均值和修正样本方差,则有
分位点
设 是连续型随机变量,其密度函数为 ,对任意给定的 ,必存在唯一的一个实数 使得
称 为分布 的 分位点(Percentiles),或 分位数.
常用的分位点符号
- 标准正态分布 的 分位点记为 .
- .
- 的 分位点记为 .
- .
- 的 分位点记为 .
- 的 分位点记为 .
- .
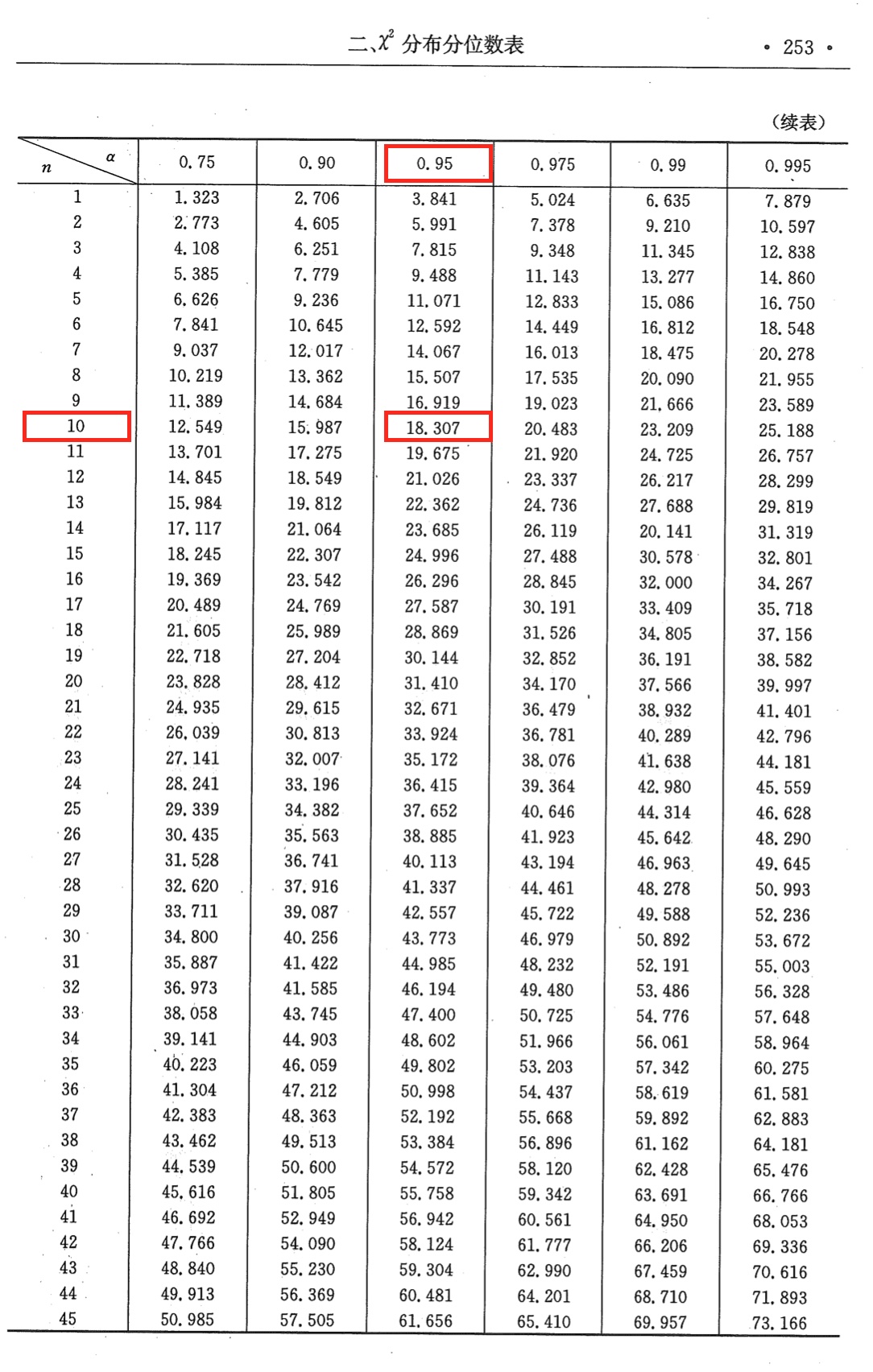
例 设 是来自正态总体 的简单随机样本,试确定常数 ,使得
解:
- ,故 , .
- 进而 .
- .
- 于是 .
- 由此可知 .
- 查表可得
- .
- 故
例 设 是来自总体 的样本,已知 是非零常数,试确定如下统计量的分布,并求出常数 .
提示:
- .
- 于是 ,.
- 进而 .
- 从而 .
- 进而可知 .
三大抽样分布的密度函数及其数字特征

补充例题
例 为来自总体 的简单随机样本. 求 的分布.
提示:,- 于是 ,.
- 进而 .
- 综上 ..
例 设 是独立同分布的 随机变量. 若
则
例 设 和 为总体 的两个独立的随机样本,且
则
例 设 是来自正态总体 的简单随机样本,记
证明:.
提示
- 由正态分布的性质 必服从正态分布,且
- ,
- ,
- 故 ,
- 于是 .
- , , 相互独立,故 与 相互独立.
- .
- 又因为 ,
- 且 与 相互独立,
- 故由 -分布的定义
例 设 是来自总体 的简单随机样本, 是来自总体 的简单随机样本,两组样本相互独立,记
求概率 .
提示
- ,而 ,故 .
- 同理 .
- 由 -分布的定义可知,.
- .
- 根据 的取值查表即可.
小结
- 总体与样本
- 样本的二重性
- 统计量及其分布
- 样本均值、样本方差、修正的样本方差
- 基本抽样分布
- 抽样分布定理
[1] 陈希孺,高等数理统计,中国科技大学出版社,2009,合肥. ↩
[2] 抛开问题的实际背景,总体就是一堆数,用一个概率分布去描述和归纳总体是恰当的,从这个意义上看,
总体就是一个分布. (茆诗松 等,概率论与数理统计(第二版),高等教育出版社,2011,北京.) ↩[3] 独立同分布常常缩写为 i.i.d.,即 Independent Identical Distribution/Distributed ↩
[4] 茆诗松 等,概率论与数理统计(第二版),高等教育出版社,2011,北京. ↩
[5] 茆诗松 等,概率论与数理统计(第二版),高等教育出版社,2011,北京. ↩
[6] 茆诗松 等,概率论与数理统计(第二版),高等教育出版社,2011,北京. ↩
[7] https://www.cnblogs.com/coshaho/p/9653460.html ↩
[8] https://en.wikipedia.org/wiki/Student%27s_t-distribution ↩
[9] https://en.wikipedia.org/wiki/F-distribution ↩
