8.2 单因子方差分析

高等工程数学 讲义 2024AU

---

---

方差分析

• ( Analysis of Variance，简称 ANOVA) ，又称 变异数分析、F-检验.
• R.A.Fisher 于 1920 年代首创.
• 方差分析有时也被归类于 试验设计与分析 这一统计学分支.
• 通过两个及两个以上样本均值差别的显著性检验，推断多组数据是否来自于同一个总体.

---

例：火箭燃料对射程的影响

对六种燃料在相同条件下分别进行多次火箭射程试验，得到如下(单位：km)

$$\begin{array}{c|cccccc} \text{试验号}\backslash\text{燃料} & A_1 & A_2 & A_3 & A_4 & A_5 & A_6 \\ \hline 1 & 87 & 90 & 56 & 55 & 92 & 75\\ 2 & 85 & 88 & 62 & 48 & 99 & 72\\ 3 & 80 & 87 & & & 95 & 81\\ 4 & & 94 & & & 91 & \\ \hline \text{均值} & 84.00 & 89.75 & 59.00 & 51.50 & 94.25 & 76.00 \end{array}$$

问：使用不同燃料的火箭射程是否存在显著差异？

---

---

分析

• 记在燃料配置为 $A_i$ 的条件下，火箭射程为 $X^{(i)}$，$i=1,2,\ldots,6$.
• 假设 $X^{(i)}\sim N(\mu_i,\sigma^2),\;j=1,2,\ldots,6$.
  
  • 注： 在方差分析中，总是假定样本取自正态总体.
• 如果燃料对火箭射程没有影响, 则 $\mu_1=\mu_2=\ldots=\mu_6$.

---

目的、条件与假设

• 目的： 研究 因子 (Factor) $A$ 对指标 $X$ 的影响.
• 已知条件与基本假设：
  
  1. $A$ 有 $a$ 个 水平 (Level) $A_1,A_2,\ldots,A_a$.
  2. 在水平 $A_i$ 下各做 $n_i\;(n_i\geq 2)$ 次 独立实验.
  3. 水平 $A_i$ 下总体 $X^{(i)}\sim N(\mu_i,\sigma^2),\;i=1,2,\ldots,a$.
     
     • $X_{i1},X_{i2},\ldots,X_{in_i}$ 为来自 $X^{(i)}$ 的样本，$i=1,2,\ldots,a$.
  4. 不同水平 $A_i$ 下的样本相互独立.

---

单因子方差分析的数学模型

• 设 $X_{i k}=\mu_{i}+\varepsilon_{i k}$, $k=1,2, \cdots, n_{i} ;\; i=1,2, \cdots, a$.
• 其中 $\varepsilon_{ik}\sim N(0,\sigma^2)$ 且相互独立.
• 记 $\mu=\frac{1}{n} \sum_{i=1}^{a} n_{i} \mu_{i},\quad n=\sum_{i=1}^{a} n_{i},\quad\delta_{i}=\mu_{i}-\mu$
• 则 $X_{i k}=\mu+\delta_{i}+\varepsilon_{i k}$, $(k=1,2, \cdots, n_{i} ; i=1,2, \cdots, a)$.
• 方差分析的统计模型本质上是一个多元正态线性回归模型.

---

$$\begin{cases} X_{11}=\mu+\delta_1+\varepsilon_{11}\\ X_{12}=\mu+\delta_1+\varepsilon_{12}\\ \quad\vdots\qquad\vdots\qquad\vdots\\ X_{1n_1}=\mu+\delta_1+\varepsilon_{1n_1}\\ X_{21}=\mu+\delta_2+\varepsilon_{21}\\ X_{22}=\mu+\delta_2+\varepsilon_{22}\\ \quad\vdots\qquad\vdots\qquad\vdots\\ X_{2n_2}=\mu+\delta_2+\varepsilon_{2n_2}\\ X_{31}=\mu+\delta_3+\varepsilon_{31}\\ \quad\vdots\qquad\vdots\qquad\vdots\\ X_{an_a}=\mu+\delta_a+\varepsilon_{an_a}\\ \end{cases} \quad\Leftrightarrow\quad \begin{bmatrix} X_{11} \\ X_{12} \\ \vdots \\ X_{1n_1} \\ X_{21} \\ X_{22} \\ \vdots \\ X_{2n_2} \\ X_{31} \\ \vdots \\ X_{an_a} \end{bmatrix} =\begin{bmatrix} 1 & 1 & 0 & \cdots & 0 \\ 1 & 1 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots\\ 1 & 1 & 0 & \cdots & 0 \\ 1 & 0 & 1 & \cdots & 0 \\ 1 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots\\ 1 & 0 & 1 & \cdots & 0 \\ 1 & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots\\ 1 & 0 & 0 & \cdots & 1 \end{bmatrix} \begin{bmatrix} \mu \\ \delta_1 \\ \delta_2 \\ \delta_3 \\ \vdots \\ \delta_a \end{bmatrix} +\begin{bmatrix} \varepsilon_{11} \\ \varepsilon_{12} \\ \vdots \\ \varepsilon_{1n_1} \\ \varepsilon_{21} \\ \varepsilon_{22} \\ \vdots \\ \varepsilon_{2n_2} \\ \varepsilon_{31} \\ \vdots \\ \varepsilon_{an_a} \end{bmatrix}$$

---

模型记号

• 水平 $A_i$ 下的样本均值: $\overline{X}_i=\frac{1}{n_{i}} \sum_{j=1}^{n_{i}} X_{ij}$.
• 水平 $A_i$ 下的样本方差：$S_{i}^{2}=\frac{1}{n_{i}} \sum_{j=1}^{n_i}\left(X_{i j}-\overline{X}_{i}\right)^{2}$.
• 所有样本的总均值：$\overline{X}=\frac{1}{n}\sum_{i=1}^{a}\sum_{j=1}^{n_{i}} X_{ij}=\dfrac{1}{n}\sum\limits_{i=1}^an_i\overline{X}_i$.

---

• 总偏差平方和（总变差） $S_{T}=\sum_{i=1}^{a} \sum_{j=1}^{n_{i}}\left(X_{ij}-\overline{X}\right)^{2}$
• 误差平方和（组内离差平方和） $S_{e}=\sum_{i=1}^{a} \sum_{j=1}^{n_{i}}\left(X_{ij}-\overline{X}_i\right)^{2}=\sum_{i=1}^{a} n_{i} S_{i}^{2}$
• 效应平方和（组间平方和） $S_{A}=\sum_{i=1}^{a} \sum_{j=1}^{n_{i}}\left(\overline{X}_{i}-\overline{X}\right)^{2}=\sum_{i=1}^{a} n_{i}\left(\overline{X}_{i}-\overline{X}\right)^{2}$

---

随机误差与系统误差

1. 同一燃料在不同试验中的射程不完全相同. 可以认为主要是受 随机因素 影响.
   
   • 造成结果波动的主要是一些不可控或不可测的因素，如：气象、时间、地理环境等.
   • 组内离差平方和 $S_e$ 在一定程度上刻画了随机误差的大小.

2. 不同燃料的射程之间的差异，可以认为主要受 因子水平 的影响.

   • 因子水平的差异主要体现为系统配置等 系统性因素，在本例中就是指不同的燃料配置.

   • 效应平方和 $S_A$ 在一定程度上就刻画了系统误差的大小.

   • 背景假设：$S_A\geq S_e$，即：随机因素对结果的影响应该不超过系统配置对结果的影响.

---

随机误差与系统误差的统计性质

• 性质1 $S_T=S_A+S_e$.
• 性质2 $\displaystyle \frac{S_{e}}{\sigma^{2}} \sim \chi^{2}(n-a)$.

提示：$\displaystyle S_{e}=\sum_{i=1}^{a} \sum_{j=1}^{n_{i}}\left(X_{ij}-\overline{X}_{i}\right)^{2}=\sum_{i=1}^{a} n_{i} S_{i}^{2}$.

• $\displaystyle \frac{n_{i} S_{i}^{2}}{\sigma^{2}} \sim \chi^{2}\left(n_{i}-1\right), (i=1,2, \cdots, a)$ 且 $S_1^2,...,S_a^2$ 相互独立,
• 故 $\displaystyle \frac{S_{e}}{\sigma^{2}}=\sum_{i=1}^{a} \frac{n_{i} S_{i}^{2}}{\sigma^{2}} \sim \chi^{2}(n-a)$.

---

• 性质3 当 $H_0:\mu_i=\mu\;(i=1,...,a)$ 成立时，$\displaystyle \frac{S_{A}}{\sigma^{2}} \sim \chi^{2}(a-1)$.

证明：

• $\displaystyle S_{A}=\sum_{i=1}^{a} n_{i}\left(\overline{X}_{i}-\overline{X}\right)^{2}=\sum_{i=1}^{a} n_{i}\left[\left(\overline{X}_{i}-\mu\right)+(\mu-\overline{X})\right]^{2}$
  
  • $\displaystyle =\sum_{i=1}^{a} n_{i}\left(\overline{X}_{i}-\mu\right)^{2}+\sum_{i=1}^{a} n_{i}(\mu-\overline{X})^{2}+2 \sum_{i=1}^{a} n_{i}\left(\overline{X}_{i}-\mu\right)(\mu-\overline{X})$
  • $\displaystyle =\sum_{i=1}^{a} n_{i}\left(\overline{X}_{i}-\mu\right)^{2}+n(\overline{X}-\mu)^{2}-2 n(\overline{X}-\mu)^{2}$
  • $\displaystyle =\sum_{i=1}^{a} n_{i}\left(\overline{X}_{i}-\mu\right)^{2}-n(\overline{X}-\mu)^{2}$

---

• $\displaystyle n(\overline{X}-\mu)^2=\frac{1}{n}\left[\sum\limits_{i=1}^an_i(\overline{X}_i-\mu)\right]^2$.
• $\displaystyle\dfrac{S_{A}}{\sigma^2}=\sum_{i=1}^{a} \left(\dfrac{\overline{X}_{i}-\mu}{\sigma/\sqrt{n_i}}\right)^{2}-n\left(\dfrac{\overline{X}-\mu}{\sigma}\right)^{2}=\sum_{i=1}^{a}Z_i^2-\frac{1}{n}\left(\sum\limits_{i=1}^a\sqrt{n_i}Z_i\right)^2$
  
  • $\displaystyle=\sum_{i=1}^{a}\frac{n-n_i}{n}Z_i^2-2\sum_{i<j}\dfrac{\sqrt{n_in_j}}{n}Z_iZ_j=\boldsymbol{Z}^{\mathrm{T}}\boldsymbol{PZ}$
  • 其中 $\boldsymbol{Z}=[Z_1\;\;Z_2\;...\;Z_a]^{\mathrm{T}}$，$\displaystyle Z_i=\frac{\overline{X}_i-\mu}{\sigma/\sqrt{n_i}},(i=1,...,a)$.
  • $H_0$ 成立时，$\boldsymbol{Z}\sim N(\boldsymbol{0},\boldsymbol{I}_a)$.

---

• $\boldsymbol{P}=\left[\begin{array}{cccc}\dfrac{n-n_1}{n} & -\dfrac{\sqrt{n_1n_2}}{n} & ... & -\dfrac{\sqrt{n_1n_a}}{n}\\ -\dfrac{\sqrt{n_2n_1}}{n} & \dfrac{n-n_2}{n} & ... & -\dfrac{\sqrt{n_2n_a}}{n}\\ \vdots & \vdots & \ddots & \vdots \\ -\dfrac{\sqrt{n_an_1}}{n} & -\dfrac{\sqrt{n_an_2}}{n} & ... & \dfrac{n-n_a}{n}\end{array}\right]$
• 可以验证 $\boldsymbol{P}$ 为对称幂等矩阵，且 $\mathrm{rank}(\boldsymbol{P})=\mathrm{tr}(\boldsymbol{P})=a-1$.
• 故存在正交矩阵 $T$，使得 $\boldsymbol{P}=\boldsymbol{T}^{\mathrm{T}}\mathrm{diag}[1\;...\;1\;\;0]\boldsymbol{T}$.
• 令 $\boldsymbol{W}=\boldsymbol{T}\boldsymbol{Z}$，则 $\boldsymbol{W}\sim N(\boldsymbol{0},\boldsymbol{I}_a)$.
• 于是 $\displaystyle\frac{S_{A}}{\sigma^2}=\boldsymbol{Z}^{\mathrm{T}}\boldsymbol{P}\boldsymbol{Z}=\boldsymbol{W}^{\mathrm{T}}\mathrm{diag}[1\;...\;1\;\;0]\boldsymbol{W}=\sum\limits_{i=1}^{a-1}W_i^2\sim\chi^2(a-1).$

---

分析

• $\displaystyle\overline{X}_i\sim N\left(\mu_i,\frac{\sigma^2}{n_i}\right)\;(i=1,...,a)$, 两两相互独立.
  
  • $E(\overline{X}_i^2)=D(\overline{X}_i)+\left[E(\overline{X}_i)\right]^2=\dfrac{\sigma^2}{n_i}+\mu_i^2$，$E(\overline{X}_i\overline{X}_j)=E(\overline{X}_i)E(\overline{X}_j)=\mu_i\mu_j$.
• $\displaystyle \overline{X}=\frac{n_1}{n}\overline{X}_1+...+\frac{n_a}{n}\overline{X}_a$ 服从正态分布.
  
  • $\displaystyle E(\overline{X})=\frac{n_1}{n}\mu_1+...+\frac{n_a}{n}\mu_a=\mu$，$\displaystyle D(\overline{X})=\frac{n_1^2}{n^2}\frac{\sigma^2}{n_1}+...+\frac{n_a^2}{n^2}\frac{\sigma^2}{n_a}=\frac{\sigma^2}{n}$.
• $\displaystyle E(\overline{X}_i\overline{X})=\frac{\sigma^2}{n}+\mu_i\mu,\quad i=1,...,a$.

---

• $E(S_A)=E\left[\sum\limits_{i=1}^an_i(\overline{X}_i-\overline{X})^2\right]=\sum\limits_{i=1}^an_i\left[E(\overline{X}_i^2)-2E(\overline{X}_i\overline{X})+E(\overline{X}^2)\right]$
  
  • $\displaystyle =\sum\limits_{i=1}^an_i\left[\frac{\sigma^2}{n_i}+\mu_i^2-2\left(\frac{\sigma^2}{n}+\mu_i\mu\right)+\frac{\sigma^2}{n}+\mu^2\right]$
  • $=(a-1)\sigma^2+\sum\limits_{i=1}^an_i(\mu_i-\mu)^2$.
• 若 $H_0$ 成立，则 $E(S_A)=(a-1)\sigma^2$
• 当 $H_0$ 不成立时，$\displaystyle \overline{S}_A=\frac{S_A}{a-1}$ 有偏大的趋势！

---

性质4 $S_A$ 与 $S_e$ 相互独立.

• 证明：
• $\displaystyle S_{e}=\sum_{i=1}^{a} \sum_{j=1}^{n_{i}}\left(X_{i j}-\overline{X}_{i}\right)^{2}=\sum_{i=1}^{a} n_{i} S_{i}^{2}$，说明 $S_{e}$ 是样本方差的函数.
• $\displaystyle S_{A}=\sum_{i=1}^{a} \sum_{j=1}^{n_{i}}\left(\overline{X}_{i}-\overline{X}\right)^{2}=\sum_{i=1}^{a} n_{i}\left(\overline{X}_{i}-\overline{X}\right)^{2}$，说明 $S_{A}$ 是样本均值的函数.
• 样本均值和样本方差是相互独立的，故 $S_e$ 和 $S_A$ 也相互独立.

---

单因子方差分析的拒绝域形式

• $\displaystyle\overline{S}_e=\frac{S_e}{n-a}$ 是 $\sigma^2$ 的无偏估计.
• 当 $H_0$ 成立时，$\displaystyle\overline{S}_A=\frac{S_A}{a-1}$ 是 $\sigma^2$ 的无偏估计.
• 当 $H_0$ 不成立时，$\overline{s}_A$ 有偏大的趋势.
• $S_e$ 和 $S_A$ 相互独立，故当 $H_0$ 成立时，$\displaystyle F=\frac{\overline{S}_{A}}{\overline{S}_{e}}=\frac{S_{A} /(a-1)}{S_{e} /(n-a)} \sim F(a-1, n-a)$.
• 所以，如果 $F$ 偏大，则可以考虑拒绝 $H_0$.

---

单因子方差分析的假设检验

定理 假设检验问题

$$H_0:\mu_1=\mu_2=\ldots=\mu_a=\mu$$

• 当 $H_0$ 成立时, $\displaystyle F=\frac{\overline{S}_{A}}{\overline{S}_{e}}=\frac{S_{A} /(a-1)}{S_{e} /(n-a)} \sim F(a-1, n-a)$.
• 拒绝域： $\displaystyle f=\frac{\overline{S}_{A}}{\overline{S}_{e}}>F_{1-\alpha}(a-1, n-a)$.

---

两个因子水平的效果比较

• 检验假设: $H_{0 i j}: \mu_{i}=\mu_{j} \quad(i, j=1,2, \cdots, a, i \neq j)$
• $H_{0ij}$ 成立时：$T_{i j}=\frac{\overline{X}_{i}-\overline{X}_{j}}{\sqrt{\dfrac{S_{e}}{n-a}\left(\dfrac{1}{n_{i}}+\dfrac{1}{n_{j}}\right)}} \sim t(n-a)$.
• $H_{0 i j}$ 不成立时，$|\overline{x}_{i}-\overline{x}_{j}|$ 有偏大趋势.
• 拒绝域： $\left|t_{i j}\right|>t_{1-\frac{a}{2}}(n-a)$.

---

方差分析表

---

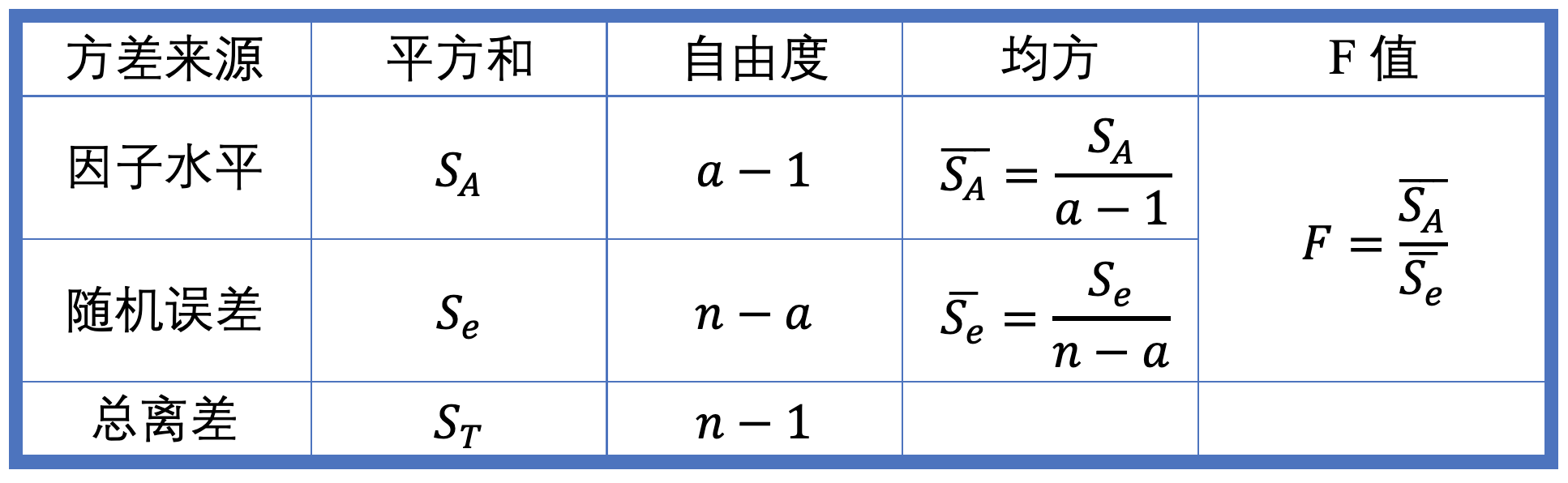
简便计算公式

• 对每一个水平下的样本计算 $\displaystyle T_{i}^{\prime}=\sum_{j=1}^{n_{i}} x_{ij},\quad T_{i}^{\prime \prime}=\sum_{j=1}^{n_{i}} x_{ij}^{2}$.
• 汇总所有水平的样本 $\displaystyle Q_{1}=\sum_{i=1}^{a} T_{i}^{\prime},\quad Q_{2}=\sum_{i=1}^{a} \sum_{j=1}^{n_{i}} x_{i j}^{2}=\sum_{i=1}^{a} T_{i}^{\prime \prime}$.
• $\displaystyle S_{T}=Q_{2}-\frac{Q_{1}^{2}}{n}$，$\displaystyle S_{A}=\sum_{i=1}^{a} \frac{T_{i}^{\prime 2}}{n_{i}}-\frac{Q_{1}^{2}}{n}$，$S_{e}=S_{T}-S_{A}$.

---

例：火箭燃料对射程的影响

对六种燃料在相同条件下分别进行多次火箭射程试验，得到如下(单位：km)

$$\begin{array}{c|cccccc} \text{试验号}\backslash\text{燃料} & A_1 & A_2 & A_3 & A_4 & A_5 & A_6 \\ \hline 1 & 87 & 90 & 56 & 55 & 92 & 75\\ 2 & 85 & 88 & 62 & 48 & 99 & 72\\ 3 & 80 & 87 & & & 95 & 81\\ 4 & & 94 & & & 91 & \\ \hline \text{均值} & 84.00 & 89.75 & 59.00 & 51.50 & 94.25 & 76.00 \end{array}$$

问：使用不同燃料的火箭射程是否存在显著差异？

---

解： 设在第 $i$ 种燃料下火箭的射程为 $X^{(i)}$，且有

$$X^{(i)}\sim N(\mu_i,\sigma^2),\;i=1,2,\ldots,6.$$

检验假设

$$H_0:\mu_1=\mu_2=\ldots=\mu_6.$$

拒绝域为

$$\dfrac{\overline{s}_{A}}{\overline{s}_{e}}=\frac{s_{A} /(6-1)}{s_{e} /(18-6)}>F_{1-\alpha}(5, 12).$$

---

$$\begin{array}{c|cccccc|l} \text{试验号}\backslash\text{燃料} & A_1 & A_2 & A_3 & A_4 & A_5 & A_6 \\ \hline 1 & 87 & 90 & 56 & 55 & 92 & 75 & \\ 2 & 85 & 88 & 62 & 48 & 99 & 72 & \\ 3 & 80 & 87 & & & 95 & 81 & \\ 4 & & 94 & & & 91 & & \\ \hline T'_j & 252 & 359 & 118 & 103 & 377 & 228 & Q_1=1437\\ T''_j & 21194 & 42249 & 6980 & 5329 & 35771 & 17370 & Q_2=118693 \end{array}$$

$\displaystyle S_{T}=Q_{2}-\frac{Q_{1}^{2}}{18}=3972.5$，$S_{A}=\sum_{i=1}^{6} \frac{T_{i}^{\prime 2}}{n_{i}}-\frac{Q_{1}^{2}}{18}=3794.5$.

---

$$\begin{array}{c|ccc|c} \text{方差来源} & \text{平方和} & \text{自由度} & \text{均方} & \text{比值}\\ \hline \text{因子（燃料）} & 3794.5 & 5 & \dfrac{3794.5}{5}=758.9 & F=\dfrac{758.9}{14.83}\\ \text{误差} & 178 & 12 & \dfrac{178}{12}=14.83 & = 51.16 \\ \hline \text{综合} & 3972.5 & 17 \end{array}$$

因为 $F=51.16>F_{0.99}(5,12)=5.06$，所以拒绝原假设. 即：认为不同燃料的射程存在显著差异.

---

小结

• 方差分析的问题背景
  
  • 与线性回归分析的关系
• 方差分析
  
  • $S_T\sim\chi^2(n-1)$, $S_e\sim\chi^2(n-a)$.
  • $H_0$ 成立时，$S_A\sim\chi^2(a-1)$.
  • 拒绝域：$\displaystyle \frac{{s}_{A}/(a-1)}{{s}_{e}/(n-a)}>F_{1-\alpha}(a-1, n-a)$.
  • 方差分析表