4.4 矩阵的奇异值分解

高等工程数学 讲义 2021

---

---

4.4.1 奇异值

引理 设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$ ，则

$$\operatorname{rank}\left(\boldsymbol{A} \boldsymbol{A}^{\mathrm{H}}\right)=\operatorname{rank}\left(\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}\right)=\operatorname{rank} \boldsymbol{A}=\mathrm{rank}\boldsymbol{A}^{\mathrm{H}}$$

---

证明思路：设 $\boldsymbol{x}$ 是齐次方程组 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}$ 的非零解.

• 于是 $\|\boldsymbol{A}\boldsymbol{x}\|^2=(\boldsymbol{A}\boldsymbol{x})^{\mathrm{H}}(\boldsymbol{A}\boldsymbol{x})=\boldsymbol{x}^{\mathrm{H}}\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{x}=0$.
• 进而可知 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}$，即 $\boldsymbol{x}$ 是 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}$ 的非零解.
• 反之，设 $\boldsymbol{x}$ 是 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}$ 的非零解.
• 显然 $\boldsymbol{x}$ 也是 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}$ 的非零解.
• 综上，$\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}$ 和 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}$ 同解，故 $\operatorname{rank}\left(\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}\right)=\operatorname{rank} \boldsymbol{A}$.
• 同理可证 $\operatorname{rank}\left(\boldsymbol{A} \boldsymbol{A}^{\mathrm{H}}\right)=\operatorname{rank} \boldsymbol{A}^{\mathrm{H}}=\operatorname{rank} \boldsymbol{A}$.

---

引理 设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$，$\boldsymbol{B} \in \mathbb{C}^{n \times m}$，则

$$|\lambda \boldsymbol{I}_m-\boldsymbol{A}\boldsymbol{B}|=\lambda^{m-n}|\lambda\boldsymbol{I}_n-\boldsymbol{B}\boldsymbol{A}|.$$

• 推论 $|\lambda \boldsymbol{I}_m-\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}|=\lambda^{m-n}|\lambda \boldsymbol{I}_n-\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}|$ 对任意的 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$ 成立.

---

引理的证明思路

• $\left|\begin{array}{cc}\lambda \boldsymbol{I}_m & \lambda \boldsymbol{A}\\ \boldsymbol{B} & \lambda \boldsymbol{I}_n\end{array}\right|=\lambda^n\left|\begin{array}{cc}\lambda \boldsymbol{I}_m & \boldsymbol{A}\\ \boldsymbol{B} & \boldsymbol{I}_n\end{array}\right|=\left|\begin{array}{cc}\lambda \boldsymbol{I}_m & \boldsymbol{A}\\ \lambda \boldsymbol{B} & \lambda \boldsymbol{I}_n\end{array}\right|$.
• 初等变换不改变矩阵的行列式，故：
• $\left|\begin{array}{cc}\lambda \boldsymbol{I}_m & \lambda \boldsymbol{A}\\ \boldsymbol{B} & \lambda \boldsymbol{I}_n\end{array}\right|=\left|\begin{array}{cc}\lambda \boldsymbol{I}_m-\boldsymbol{A}\boldsymbol{B} & \boldsymbol{O}\\ \boldsymbol{B} & \lambda \boldsymbol{I}_n\end{array}\right|=\lambda^n|\lambda \boldsymbol{I}_m-\boldsymbol{A}\boldsymbol{B}|$.
• $\left|\begin{array}{cc}\lambda \boldsymbol{I}_m & \boldsymbol{A}\\ \lambda \boldsymbol{B} & \lambda \boldsymbol{I}_n\end{array}\right|=\left|\begin{array}{cc}\lambda \boldsymbol{I}_m & \boldsymbol{A}\\ \boldsymbol{O} & \lambda \boldsymbol{I}_n-\boldsymbol{B}\boldsymbol{A}\end{array}\right|=\lambda^m|\lambda \boldsymbol{I}_n-\boldsymbol{B}\boldsymbol{A}|$.
• 故 $\lambda^n|\lambda \boldsymbol{I}_m-\boldsymbol{A}\boldsymbol{B}|=\lambda^m|\lambda \boldsymbol{I}_n-\boldsymbol{B}\boldsymbol{A}|$.

---

引理 设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$，则 $\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}$ 和 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}$ 的特征值均非负。

• 证明思路：设 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{\xi}_i=\lambda_i\boldsymbol{\xi}_i\;(\boldsymbol{\xi}_i\ne \boldsymbol{0})$.
• 于是 $\lambda_i\|\boldsymbol{\xi}\|_2^2=\lambda_i\boldsymbol{\xi}^{\mathrm{H}}\boldsymbol{\xi}=\boldsymbol{\xi}^{\mathrm{H}}\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{\xi}=\|\boldsymbol{A}\boldsymbol{\xi}_i\|_2^2\geq0$.
• 由此可知 $\lambda_i\geq 0$.
• 同理可证 $\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}$ 的特征值均非负.

---

推论 设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$ ，则 $\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}$ 和 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}$ 有相同的正特征值.

• 证明思路：$|\lambda \boldsymbol{I}_m-\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}|=\lambda^{m-n}|\lambda \boldsymbol{I}_n-\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}|$.
• 这意味着 $\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}$ 和 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}$ 有相同的非零特征值.
• $\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}$ 和 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}$ 特征值均非负，故二者必有相同的正特征值.
• 该推论说明：$\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}$ 和 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}$ 最多只是零特征值的个数不同.

---

讨论： 设 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{\xi}_i=\lambda_i\boldsymbol{\xi}_i\;(\boldsymbol{\xi}_i\ne \boldsymbol{0})$

1. 若 $\lambda_i>0$，则必有 $\boldsymbol{A}\boldsymbol{\xi}_i\ne\boldsymbol{0}$.
   
   • 由 $\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{\xi}_i=\boldsymbol{A}\lambda_i\boldsymbol{\xi}_i=\lambda_i\boldsymbol{A}\boldsymbol{\xi}_i$ 可知 $\lambda_i$ 也是 $\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}$ 的特征值.
   • 由此不难看出 $\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}$ 和 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}$ 有相同的正特征值.
2. 若 $\lambda_i=0$，即 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{\xi}_i=\lambda_i\boldsymbol{\xi}_i=\boldsymbol{0}$.
   
   • 因为 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}$ 和 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}$ 同解，故 $\boldsymbol{A}\boldsymbol{\xi}_i=\boldsymbol{0}$.
   • 零向量不能作为特征向量，故此时由 $\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{\xi}_i=\lambda_i\boldsymbol{A}\boldsymbol{\xi}_i$ 无法推出 $\lambda_i=0$ 也是 $\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}$ 的特征值.

---

奇异值

设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$，$\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}$ 的特征值为 $\lambda_1,\lambda_2,\ldots,\lambda_n$，则

$$\sigma_{i}=\sqrt{\lambda_{i}}\quad (i=1,2,\ldots,n)$$

称为 $\boldsymbol{A}$ 的 奇异值 (Singular Value).

• 注： $\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}$ 与 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}$ 虽然特征值个数可能不同，但有完全一致的正特征值. 为了统一表述，在很多场合，奇异值特指正奇异值.

---

例 求 $\boldsymbol{A}=\left[\begin{array}{ll}{1} & {2} \\ {0} & {0} \\ \mathrm{i} & {0}\end{array}\right]$ 的奇异值.

• 提示：$\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}=\left[\begin{array}{ccc}{1} & {0} & {-\mathrm{i}} \\ {2} & {0} & {0}\end{array}\right]\left[\begin{array}{cc}{1} & {2} \\ {0} & {0} \\ {\mathrm{i}} & {0}\end{array}\right]=\left[\begin{array}{cc}{2} & {2} \\ {2} & {4}\end{array}\right]$.
• $\left|\lambda \boldsymbol{I}-\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}\right|=\left|\begin{array}{cc}{\lambda-2} & {-2} \\ {-2} & {\lambda-4}\end{array}\right|=\lambda^{2}-6 \lambda+4$.
• $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}$ 的特征值： $\lambda_{1}=3+\sqrt{5}, \quad \lambda_{2}=3-\sqrt{5}$.
• $\boldsymbol{A}$ 的奇异值： $\sigma_{1}=\sqrt{\lambda_{1}}=\sqrt{3+\sqrt{5}}, \quad \sigma_{2}=\sqrt{\lambda_{2}}=\sqrt{3-\sqrt{5}}$.

---

例 求 $\boldsymbol{A}=\left[\begin{array}{llll}{1} & {0} & {1} & \mathrm{i} \\ {0} & \mathrm{i} & {0} & {0}\end{array}\right]$ 的奇异值.

---

提示

• $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}=\left[\begin{array}{cc}{1} & {0} \\ {0} & {-\mathrm{i}} \\ {1} & {0} \\ {-\mathrm{i}} & {0}\end{array}\right]\left[\begin{array}{cccc}{1} & {0} & {1} & {\mathrm{i}} \\ {0} & {\mathrm{i}} & {0} & {0}\end{array}\right]=\left[\begin{array}{cccc}{1} & {0} & {1} & {\mathrm{i}} \\ {0} & {1} & {0} & {0} \\ {1} & {0} & {1} & {\mathrm{i}} \\ {-\mathrm{i}} & {0} & {-\mathrm{i}} & {1}\end{array}\right]$
• $\left|\lambda \boldsymbol{I}-\boldsymbol{A}^\mathrm{H} \boldsymbol{A}\right|=\left|\begin{array}{cccc}{\lambda-1} & {0} & {-1} & {-\mathrm{i}} \\ {0} & {\lambda-1} & {0} & {0} \\ {-1} & {0} & {\lambda-1} & {-\mathrm{i}} \\ {\mathrm{i}} & {0} & {\mathrm{i}} & {\lambda-1}\end{array}\right|=(\lambda-3)(\lambda-1) \lambda^{2}$
• $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}$ 的特征值： $\lambda_{1}=3, \lambda_{2}=1, \lambda_{3}=\lambda_{4}=0$.
• $\boldsymbol{A}$ 的奇异值： $\sigma_{1}=\sqrt{3}, \quad \sigma_{2}=1, \sigma_{3}=\sigma_{4}=0$.

---

另一种解法

• $\boldsymbol{A} \boldsymbol{A}^{\mathrm{H}}=\left[\begin{array}{cccc}{1} & {0} & {1} & {\mathrm{i}} \\ {0} & {\mathrm{i}} & {0} & {0}\end{array}\right]\left[\begin{array}{cc}{1} & {0} \\ {0} & {-\mathrm{i}} \\ {1} & {0} \\ {-\mathrm{i}} & {0}\end{array}\right]=\left[\begin{array}{cc}{3} & {0} \\ {0} & {1}\end{array}\right]$
• $\left|\lambda \boldsymbol{I}-\boldsymbol{A} \boldsymbol{A}^{\mathrm{H}}\right|=\left|\begin{array}{rr}{\lambda-3} & {0} \\ {0} & {\lambda-1}\end{array}\right|=(\lambda-3)(\lambda-1)$
• $\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}$ 的特征值： $\lambda_1=3,\lambda_2=1$.
• 因为 $\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}$ 和 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}$ 有相同的正特征值, 而 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}$ 是 $4$ 阶方阵，故 $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}$ 的全部特征值为 $\lambda_{1}=3, \lambda_{2}=1, \lambda_{3}=\lambda_{4}=0$.
• $\boldsymbol{A}$ 的奇异值： $\sigma_{1}=\sqrt{3}, \quad \sigma_{2}=1, \sigma_{3}=\sigma_{4}=0$.

---

4.4.2 奇异值分解

设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$ ， $\operatorname{rank} \boldsymbol{A}=r>0$ ，则存在 $m$ 阶酉矩阵 $\boldsymbol{U}$ 和 $n$ 阶酉矩阵 $\boldsymbol{V}$ ，使得

$$\boldsymbol{U}^{\mathrm{H}} \boldsymbol{A} \boldsymbol{V}=\left[\begin{array}{ll}\boldsymbol{\Sigma} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right]$$

• 其中 $\boldsymbol{\Sigma}=\operatorname{diag}\left\{\sigma_{1}, \sigma_{2}, \cdots, \sigma_{r}\right\}$，$\sigma_{1} \geq \sigma_{2} \geq \cdots \geq \sigma_{r}>0$ 是 $\boldsymbol{A}$ 的正(非零)奇异值.
• 上式称为 $\boldsymbol{A}$ 的 奇异值分解（Singular Value Decomposition，简称 SVD）

---

证明思路：

• $\operatorname{rank} \boldsymbol{A}=r>0$ ，故 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}$ 有 $r$ 个正特征值.
• 设 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}$ 的所有特征值为 $\sigma_{1}^{2} \geq \sigma_{2}^{2} \geq \cdots \geq \sigma_{r}^{2}>\sigma_{r+1}^{2}=\cdots=\sigma_{n}^{2}=0$.
• 因为 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}$ 是 Hermite 矩阵，故存在 $n$ 阶酉矩阵 $\boldsymbol{V}$ ，使得 $\boldsymbol{V}^{\mathrm{H}}\left(\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}\right) \boldsymbol{V}$ 是对角阵.
• $\boldsymbol{V}^{\mathrm{H}} \boldsymbol{A}^{\mathrm{H}} \boldsymbol{A} \boldsymbol{V}=\mathrm{diag}\{\sigma_1^2,\sigma_2^2,\ldots,\sigma_n^2\} \triangleq\left[\begin{array}{cc}{\boldsymbol{\Sigma}^{2}} & {} \\ {} & \boldsymbol{O}\end{array}\right]$.
• 其中 $\boldsymbol{\Sigma}=\operatorname{diag}\left\{\sigma_{1}, \sigma_{2}, \cdots, \sigma_{r}\right\}$.

---

• 记 $\boldsymbol{V}=[\boldsymbol{v}_1\;\boldsymbol{v}_2\;\ldots\;\boldsymbol{v}_n]$，$\boldsymbol{V}$ 的列向量为单位正交特征向量.
• 记 $\boldsymbol{V}_{1}=[\boldsymbol{v}_1\;\boldsymbol{v}_2\;\ldots\;\boldsymbol{v}_r], \boldsymbol{V}_{2}=[\boldsymbol{v}_{r+1}\;\boldsymbol{v}_{r+2}\;\ldots\;\boldsymbol{v}_n]$.
• $\boldsymbol{V}^{\mathrm{H}}\left(\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}\right) \boldsymbol{V}=\left[\begin{array}{c}{\boldsymbol{V}_{1}^{\mathrm{H}}} \\ {\boldsymbol{V}_{2}^{\mathrm{H}}}\end{array}\right]\left(\boldsymbol{A}^\mathrm{H} \boldsymbol{A}\right)\left[\boldsymbol{V}_{1}\; \boldsymbol{V}_{2}\right]$
• $=\left[\begin{array}{cc}{\boldsymbol{V}_{1}^{\mathrm{H}}\left(\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}\right) \boldsymbol{V}_{1}} & {\boldsymbol{V}_{1}^{\mathrm{H}}\left(\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}\right) \boldsymbol{V}_{2}} \\ {\boldsymbol{V}_{2}^{\mathrm{H}}\left(\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}\right) \boldsymbol{V}_{1}} & {\boldsymbol{V}_{2}^{\mathrm{H}}\left(\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}\right) \boldsymbol{V}_{2}}\end{array}\right]=\left[\begin{array}{cc}{\boldsymbol{\Sigma}^{2}} & {} \\ {} & \boldsymbol{O}\end{array}\right]$.
• $\Leftrightarrow \left\{\begin{array}{l}{{\boldsymbol{V}_{1}^{\mathrm{H}}\left(\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\right)\boldsymbol{V}_{1}}=\boldsymbol{\Sigma}^2 \\ {\boldsymbol{V}_{1}^{\mathrm{H}}\left(\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}\right) \boldsymbol{V}_{2}}=\boldsymbol{O}} \\ {\boldsymbol{V}_{2}^{\mathrm{H}}\left(\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}\right) \boldsymbol{V}_{1}=\boldsymbol{O}} \\ {\boldsymbol{V}_{2}^{\mathrm{H}}\left(\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}\right) \boldsymbol{V}_{2}=\boldsymbol{O}}\end{array}\right.$
• 记 $\boldsymbol{U}_1=\boldsymbol{A}\boldsymbol{V}_1\boldsymbol{\Sigma}^{-1}=[\boldsymbol{u}_1\;\boldsymbol{u}_2\;\ldots\;\boldsymbol{u}_r]\in\mathbb{C}^{m\times r}$.
• 由 $\boldsymbol{U}_1^{\mathrm{H}}\boldsymbol{U}_1=\boldsymbol{I}_r$ 可知 ${\boldsymbol{u}_{1}}, {\boldsymbol{u}_{2}}, {\dots}, {\boldsymbol{u}_{r}}$ 是 $\mathbb{C}^m$ 中两两正交的单位向量.
• 将 ${\boldsymbol{u}_{1}}, {\dots}, {\boldsymbol{u}_{r}}$ 扩张为标准正交基 $\boldsymbol{u}_{1}, \ldots, \boldsymbol{u}_{m}$.
• 记 $\boldsymbol{U}_{2}=[\boldsymbol{u}_{r+1}\;\boldsymbol{u}_{r+2}\;\ldots\;\boldsymbol{u}_m]$ ，则 $\boldsymbol{U}_2^{\mathrm{H}}\boldsymbol{U}_1=\boldsymbol{O}$.

---

• $\boldsymbol{U}^{\mathrm{H}} \boldsymbol{A} \boldsymbol{V}=\left[\begin{array}{c}{\boldsymbol{U}_{1}^{\mathrm{H}}} \\ {\boldsymbol{U}_{2}^{\mathrm{H}}}\end{array}\right] \boldsymbol{A}\left[\begin{array}{cc}{\boldsymbol{V}_{1}} & {\boldsymbol{V}_{2}}\end{array}\right] =\left[\begin{array}{ll}{\boldsymbol{U}_{1}^{\mathrm{H}} \boldsymbol{A} \boldsymbol{V}_{1}} & {\boldsymbol{U}_{1}^{\mathrm{H}} \boldsymbol{A} \boldsymbol{V}_{2}} \\ {\boldsymbol{U}_{2}^{\mathrm{H}} \boldsymbol{A} \boldsymbol{V}_{1}} & {\boldsymbol{U}_{2}^{\mathrm{H}} \boldsymbol{A} \boldsymbol{V}_{2}}\end{array}\right]$
• $=\left[\begin{array}{cc}{\boldsymbol{U}_{1}^{\mathrm{H}} \boldsymbol{A} \boldsymbol{V}_{1} \boldsymbol{\Sigma}^{-1} \boldsymbol{\Sigma}} & {\boldsymbol{U}_{1}^{\mathrm{H}} \boldsymbol{A} \boldsymbol{V}_{2}} \\ {\boldsymbol{U}_{2}^{\mathrm{H}} \boldsymbol{A} \boldsymbol{V}_{1} \boldsymbol{\Sigma}^{-1} \boldsymbol{\Sigma}} & {\boldsymbol{U}_{2}^{\mathrm{H}} \boldsymbol{A} \boldsymbol{V}_{2}}\end{array}\right]=\left[\begin{array}{ll}{\boldsymbol{U}_1^{\mathrm{H}}\boldsymbol{U}_1\boldsymbol{\Sigma}} & \boldsymbol{O} \\ {\boldsymbol{U}_2^{\mathrm{H}}\boldsymbol{U}_1\boldsymbol{\Sigma}} & \boldsymbol{O}\end{array}\right]=\left[\begin{array}{ll}\boldsymbol{\Sigma} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right]$.
• 以上即为 $\boldsymbol{A}$ 的奇异值分解.

---

4.4.3 奇异值分解的求解

1. 求 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}$ 的特征值以及对应单位正交特征向量：
   
   • $\lambda_{1} \geq \lambda_{2} \geq \cdots \geq \lambda_{r}>\lambda_{r+1}=\cdots=\lambda_{n}=0$.
   • $\boldsymbol{v}_{1}, \boldsymbol{v}_{2}, \cdots, \boldsymbol{v}_{r}, \boldsymbol{v}_{r+1}, \cdots, \boldsymbol{v}_{n}$.
2. 记 $\boldsymbol{V}_{1}=\left[\begin{array}{llll}{\boldsymbol{v}_{1}} & {\dots} & {\boldsymbol{v}_{r}}\end{array}\right]$, $\boldsymbol{V}_{2}=\left[\begin{array}{lll}{\boldsymbol{v}_{r+1}} & {\dots} & {\boldsymbol{v}_{n}}\end{array}\right]$, $\boldsymbol{V}=\left[\begin{array}{ll}{\boldsymbol{V}_{1}} & {\boldsymbol{V}_{2}}\end{array}\right]$, $\boldsymbol{\Sigma}=\mathrm{diag}\{\sqrt{\lambda_1},\sqrt{\lambda_2},\ldots,\sqrt{\lambda_r}\}$，令 $\boldsymbol{U}_1=\boldsymbol{AV}_1\boldsymbol{\Sigma}^{-1}$.
3. 将 $\boldsymbol{U}_1$ 的列向量扩张成 $\mathbb{C}^m$ 的标准正交基 $\boldsymbol{u}_{1}, \ldots, \boldsymbol{u}_{r}, \boldsymbol{u}_{r+1}, \ldots, \boldsymbol{u}_{m}$，令 ${\boldsymbol{U}}=[\boldsymbol{u}_1,...,\boldsymbol{u}_m]$.
4. $\boldsymbol{U}^\mathrm{H} \boldsymbol{A} \boldsymbol{V}=\left[\begin{array}{ll}{\boldsymbol{\Sigma}} & {0} \\ {0} & {0}\end{array}\right]$

---

例 求 $\boldsymbol{A}=\left[\begin{array}{ll}{2} & {1} \\ {0} & {2} \\ {1} & {0}\end{array}\right]$ 的奇异值分解.

---

• 提示：$\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}=\left[\begin{array}{lll}{2} & {0} & {1} \\ {1} & {2} & {0}\end{array}\right]\left[\begin{array}{ll}{2} & {1} \\ {0} & {2} \\ {1} & {0}\end{array}\right]=\left[\begin{array}{ll}{5} & {2} \\ {2} & {5}\end{array}\right]$.
• $\left|\lambda \boldsymbol{I}-\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}\right|=\left|\begin{array}{cc}{\lambda-5} & {-2} \\ {-2} & {\lambda-5}\end{array}\right|=(\lambda-7)(\lambda-3)$，故 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}$ 的特征值为 $\lambda_{1}=7, \lambda_{2}=3$.
• 由 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}-\lambda_{1} \boldsymbol{I}=\left[\begin{array}{cc}{-2} & {2} \\ {2} & {-2}\end{array}\right]$，解得 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}$ 关于 $\lambda_1=7$ 的特征向量 $\boldsymbol{v}_{1}=\frac{1}{\sqrt{2}}\left[\begin{array}{l}{1} \\ {1}\end{array}\right]$.
• 由 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}-\lambda_{2} \boldsymbol{I}=\left[\begin{array}{ll}{2} & {2} \\ {2} & {2}\end{array}\right]$ 解得 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}$ 关于 $\lambda_2=3$ 的特征向量 $\boldsymbol{v}_{2}=\frac{1}{\sqrt{2}}\left[\begin{array}{c}{1} \\ {-1}\end{array}\right]$.

---

• 令 $\boldsymbol{V}=\boldsymbol{V}_{1}=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}{1} & {1} \\ {1} & {-1}\end{array}\right]$ ， $\boldsymbol{\Sigma}=\left[\begin{array}{cc}{\sqrt{7}} & {0} \\ {0} & {\sqrt{3}}\end{array}\right]$,
• $\boldsymbol{U}_{1}=\boldsymbol{A} \boldsymbol{V}_{1} \boldsymbol{\Sigma}^{-1}=\left[\begin{array}{cc}{\frac{3}{\sqrt{14}}} & {\frac{1}{\sqrt{6}}} \\ {\frac{2}{\sqrt{14}}} & {-\frac{2}{\sqrt{6}}} \\ {\frac{1}{\sqrt{14}}} & {\frac{1}{\sqrt{6}}}\end{array}\right]=\left[\begin{array}{cc}{\boldsymbol{u}_{1}} & {\boldsymbol{u}_{2}}\end{array}\right]$.
• 将 $\boldsymbol{U}_1$ 的列向量 $\boldsymbol{u}_1,\boldsymbol{u}_2$ 扩张成 $\mathbb{R}^3$ 中的标准正交基:
• 设 $\boldsymbol{u}_{3}=[x_1\;x_2\;x_3]^{\mathrm{T}}$，满足 $\left\{\begin{array}{l}{3 x_{1}+2 x_{2}+x_{3}=0} \\ {x_{1}-2 x_{2}+x_{3}=0} \\ {\left|x_{1}\right|^{2}+\left|x_{2}\right|^{2}+\left|x_{3}\right|^{2}=1}\end{array}\right.$
• 解之得 $\boldsymbol{u}_{3}=\frac{1}{\sqrt{21}}[2\;\; -1\;\;-4]^{\mathrm{T}}$.

---

• 令 $\boldsymbol{U}=[\boldsymbol{u}_1\;\boldsymbol{u}_2\;\boldsymbol{u}_3]=\left[\begin{array}{ccc}{\frac{3}{\sqrt{14}}} & {\frac{1}{\sqrt{6}}} & {\frac{2}{\sqrt{21}}} \\ {\frac{2}{\sqrt{14}}} & {-\frac{2}{\sqrt{6}}} & {-\frac{1}{\sqrt{21}}} \\ {\frac{1}{\sqrt{14}}} & {\frac{1}{\sqrt{6}}} & {-\frac{4}{\sqrt{21}}}\end{array}\right]$
• 综上，$\boldsymbol{A}$ 的奇异值分解为：
• $\boldsymbol{A}=\left[\begin{array}{ll}{2} & {1} \\ {0} & {2} \\ {1} & {0}\end{array}\right]=\boldsymbol{U}\left[\begin{array}{ll}\boldsymbol{\Sigma} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right] \boldsymbol{V}^{\mathrm{H}}$
  
  • $=\left[\begin{array}{ccc}{\frac{3}{\sqrt{14}}} & {\frac{1}{\sqrt{6}}} & {\frac{2}{\sqrt{21}}} \\ {\frac{2}{\sqrt{14}}} & {-\frac{2}{\sqrt{6}}} & {-\frac{1}{\sqrt{21}}} \\ {\frac{1}{\sqrt{14}}} & {\frac{1}{\sqrt{6}}} & {-\frac{4}{\sqrt{21}}}\end{array}\right]\left[\begin{array}{cc}{\sqrt{7}} & {0} \\ {0} & {\sqrt{3}} \\ {0} & {0}\end{array}\right]\left[\begin{array}{cc}{\frac{1}{\sqrt{2}}} & {\frac{1}{\sqrt{2}}} \\ {\frac{1}{\sqrt{2}}} & {-\frac{1}{\sqrt{2}}}\end{array}\right]$.

---

注：

设 $\boldsymbol{A}$ 的 SVD 为

$$\boldsymbol{U}^\mathrm{H} \boldsymbol{A} \boldsymbol{V}=\left[\begin{array}{ll}\boldsymbol{\Sigma} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right]$$

• $\boldsymbol{V}$ 的列向量是方阵 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}$ 的标准正交特征向量.
• 显然 $\boldsymbol{A}^{\mathrm{H}}$ 的 SVD 为 $\boldsymbol{V}^\mathrm{H} \boldsymbol{A}^\mathrm{H} \boldsymbol{U}=\left[\begin{array}{ll}\boldsymbol{\Sigma} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right]$.
• 由此可知 $\boldsymbol{U}$ 的列向量是 $\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}$ 的标准正交特征向量.
• 问：是否可以以此为基础得到一个求解 $\boldsymbol{U}$ 和 $\boldsymbol{V}$ 的新方法？

---

例 求 $\boldsymbol{A}=\left[\begin{array}{rrrr}{1} & {0} & {0} & {-1} \\ {0} & {1} & {0} & {1}\end{array}\right]$ 的奇异值分解.

---

提示

• $\boldsymbol{A} \boldsymbol{A}^{\mathrm{H}}=\left[\begin{array}{rrrr}{1} & {0} & {0} & {-1} \\ {0} & {1} & {0} & {1}\end{array}\right]\left[\begin{array}{rr}{1} & {0} \\ {0} & {1} \\ {0} & {0} \\ {-1} & {1}\end{array}\right]=\left[\begin{array}{cc}{2} & {-1} \\ {-1} & {2}\end{array}\right]$.
• $\left|\lambda \boldsymbol{I}-\boldsymbol{A} \boldsymbol{A}^{\mathrm{H}}\right|=\left|\begin{array}{cc}{\lambda-2} & {1} \\ {1} & {\lambda-2}\end{array}\right|=(\lambda-3)(\lambda-1)$，故 ${\boldsymbol{A}} {\boldsymbol{A}}^{\mathrm{H}}$ 的特征值为 $\lambda_{1}=3, \lambda_{2}=1$.
• 由 $\boldsymbol{A} \boldsymbol{A}^{\mathrm{H}}-\lambda_{1} \boldsymbol{I}=\left[\begin{array}{cc}{-1} & {-1} \\ {-1} & {-1}\end{array}\right]$ 解得 $\boldsymbol{A} \boldsymbol{A}^{\mathrm{H}}$ 关于 $\lambda_1=3$ 的单位特征向量 $\boldsymbol{u}_{1}=\frac{1}{\sqrt{2}}\left[\begin{array}{c}{1} \\ {-1}\end{array}\right]$.

---

• 由 $\boldsymbol{A} \boldsymbol{A}^{\mathrm{H}}-\lambda_{2} \boldsymbol{I}=\left[\begin{array}{cc}{1} & {-1} \\ {-1} & {1}\end{array}\right]$ 解得 $\boldsymbol{A} \boldsymbol{A}^{\mathrm{H}}$ 关于 $\lambda_2=1$ 的单位特征向量 $\boldsymbol{u}_{2}=\frac{1}{\sqrt{2}}\left[\begin{array}{l}{1} \\ {1}\end{array}\right]$.
• 令 $\boldsymbol{U}=[\boldsymbol{u}_1\;\boldsymbol{u}_2]=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}{1} & {1} \\ {-1} & {1}\end{array}\right],\; \boldsymbol{\Sigma}=\left[\begin{array}{cc}{\sqrt{3}} & {0} \\ {0} & {1}\end{array}\right]$.
• 又 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}$ 的所有特征值 $\lambda_{1}=3, \quad \lambda_{2}=1, \quad \lambda_{3}=\lambda_{4}=0$.
• $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}=\left[\begin{array}{cc}{1} & {0} \\ {0} & {1} \\ {0} & {0} \\ {-1} & {1}\end{array}\right]\left[\begin{array}{cccc}{1} & {0} & {0} & {-1} \\ {0} & {1} & {0} & {1}\end{array}\right]=\left[\begin{array}{cccc}{1} & {0} & {0} & {-1} \\ {0} & {1} & {0} & {1} \\ {0} & {0} & {0} & {0} \\ {-1} & {1} & {0} & {2}\end{array}\right].$

---

• 由 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}-\lambda_{1} \boldsymbol{I}=\left[\begin{array}{cccc}{-2} & {0} & {0} & {-1} \\ {0} & {-2} & {0} & {1} \\ {0} & {0} & {-3} & {0} \\ {-1} & {1} & {0} & {-1}\end{array}\right]$ 解得 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}$ 关于特征值 $\lambda_1=3$ 的单位特征向量 $\boldsymbol{v}_{1}=\frac{1}{\sqrt{6}}\left[\begin{array}{llll}{-1} & {1} & {0} & {2}\end{array}\right]^{\mathrm{T}}$.
• 由 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}-\lambda_{2} \boldsymbol{I}=\left[\begin{array}{cccc}{0} & {0} & {0} & {-1} \\ {0} & {0} & {0} & {1} \\ {0} & {0} & {-1} & {0} \\ {-1} & {1} & {0} & {1}\end{array}\right]$ 解得 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}$ 关于特征值 $\lambda_2=1$ 的单位特征向量 $\boldsymbol{v}_{2}=\frac{1}{\sqrt{2}}\left[\begin{array}{llll}{1} & {1} & {0} & {0}\end{array}\right]^{\mathrm{T}}$.

---

• 由 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}-\lambda_{3} \boldsymbol{I}=\left[\begin{array}{rrrr}{1} & {0} & {0} & {-1} \\ {0} & {1} & {0} & {1} \\ {0} & {0} & {0} & {0} \\ {-1} & {1} & {0} & {2}\end{array}\right]$ 解得 $\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}$ 关于特征值 $\lambda_3=0$ 的单位正交特征向量 $\boldsymbol{v}_{3}=\left[\begin{array}{llll}{0} & {0} & {1} & {0}\end{array}\right]^{\mathrm{T}}, \; \boldsymbol{v}_{4}=\frac{1}{\sqrt{3}}\left[\begin{array}{llll}{1} & {-1} & {0} & {1}\end{array}\right]^{\mathrm{T}}$
• 令 $\boldsymbol{V}=[\boldsymbol{v}_1\;\boldsymbol{v}_2\;\boldsymbol{v}_3\;\boldsymbol{v}_4]$.

---

• $\boldsymbol{U}\left[\begin{array}{cc}\boldsymbol{\Sigma} & {0} \\ {0} & {0}\end{array}\right] \boldsymbol{V}^{\mathrm{H}}$
  
  • $=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}{1} & {1} \\ {-1} & {1}\end{array}\right]\left[\begin{array}{cccc}{\sqrt{3}} & {0} & {0} & {0} \\ {0} & {1} & {0} & {0}\end{array}\right]\left[\begin{array}{cccc}{\frac{-1}{\sqrt{6}}} & {\frac{1}{\sqrt{6}}} & {0} & {\frac{2}{\sqrt{6}}} \\ {\frac{1}{\sqrt{2}}} & {\frac{1}{\sqrt{2}}} & {0} & {0} \\ {0} & {0} & {1} & {0} \\ {\frac{1}{\sqrt{3}}} & {\frac{-1}{\sqrt{3}}} & {0} & {\frac{1}{\sqrt{3}}}\end{array}\right]$
  • $=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}{1} & {1} \\ {-1} & {1}\end{array}\right]\left[\begin{array}{cccc}{\frac{-1}{\sqrt{2}}} & {\frac{1}{\sqrt{2}}} & {0} & {\sqrt{2}} \\ {\frac{1}{\sqrt{2}}} & {\frac{1}{\sqrt{2}}} & {0} & {0}\end{array}\right]$
  • $=\left[\begin{array}{cccc}{0} & {1} & {0} & {1} \\ {1} & {0} & {0} & {-1}\end{array}\right]\neq\left[\begin{array}{rrrr}{1} & {0} & {0} & {-1} \\ {0} & {1} & {0} & {1}\end{array}\right]=\boldsymbol{A}$

---

问题出在哪里？

• 若取 $\boldsymbol{A} \boldsymbol{A}^{\mathrm{H}}$ 关于 $\lambda_1=3$ 的单位特征向量为 $\tilde{\boldsymbol{u}}_{1}=-\boldsymbol{u}_1=\frac{1}{\sqrt{2}}\left[\begin{array}{c}{-1} \\ {1}\end{array}\right]$，再令 $\boldsymbol{U}=[\tilde{\boldsymbol{u}}_1\;\boldsymbol{u}_2]$，则
• $\boldsymbol{U}\left[\begin{array}{cc}\boldsymbol{\Sigma} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right] \boldsymbol{V}^{\mathrm{H}}=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}{-1} & {1} \\ {1} & {1}\end{array}\right]\left[\begin{array}{cccc}{\sqrt{3}} & {0} & {0} & {0} \\ {0} & {1} & {0} & {0}\end{array}\right]\left[\begin{array}{cccc}{\frac{-1}{\sqrt{6}}} & {\frac{1}{\sqrt{6}}} & {0} & {\frac{2}{\sqrt{6}}} \\ {\frac{1}{\sqrt{2}}} & {\frac{1}{\sqrt{2}}} & {0} & {0} \\ {0} & {0} & {1} & {0} \\ {\frac{1}{\sqrt{3}}} & {\frac{-1}{\sqrt{3}}} & {0} & {\frac{1}{\sqrt{3}}}\end{array}\right]$
• $=\left[\begin{array}{llll}{1} & {0} & {0} & {-1} \\ {0} & {1} & {0} & {1}\end{array}\right]=\boldsymbol{A}$
• 标准正交特征向量组不具有唯一性，如果随意进行选择，可能导致得不到正确的 SVD

---

4.4.4 奇异值分解的应用

1. 最小二乘问题 (Least Squares Problem)
2. 数据/图像压缩 (Data/Image Compression)
3. 潜在语义索引 (Latent Semantic Indexing)

---

最小二乘问题

设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$ ， $\boldsymbol{b} \in \mathbb{C}^{m}$ ，求 $\boldsymbol{x}^{*} \in \mathbb{C}^{n}$ ，使得

$$\left\|\boldsymbol{A} \boldsymbol{x}^{*}-\boldsymbol{b}\right\|_{2}=\min _{\boldsymbol{x} \in \mathbb{C}^{n}}\|\boldsymbol{A} \boldsymbol{x}-\boldsymbol{b}\|_{2}$$

• 设 $\boldsymbol{A}$ 的奇异值分解为 $\boldsymbol{A}=\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\mathrm{H}}$，于是
• $\boldsymbol{A} \boldsymbol{x}-\boldsymbol{b}=\boldsymbol{U} \boldsymbol{\Sigma V}^{\mathrm{H}}\boldsymbol{x}-\boldsymbol{b}=\boldsymbol{U}\left(\boldsymbol{\Sigma V}^{\mathrm{H}} \boldsymbol{x}-\boldsymbol{U}^{\mathrm{H}}\boldsymbol{b}\right)$.
• 令 $\boldsymbol{y}=\boldsymbol{V}^\mathrm{H}\boldsymbol{x}, \boldsymbol{c}=\boldsymbol{U}^\mathrm{H}\boldsymbol{b}$，则上式可化为 $\boldsymbol{A}\boldsymbol{x}-\boldsymbol{b}=\boldsymbol{U}(\boldsymbol{\Sigma} \boldsymbol{y}-\boldsymbol{c})$.

---

• 关于 $\boldsymbol{A} \boldsymbol{x}-\boldsymbol{b}=\boldsymbol{U}(\boldsymbol{\Sigma} \boldsymbol{y}-\boldsymbol{c})$ 的求解：
• $\boldsymbol{U}$ 是酉矩阵，不改变向量的长度(2-范数).
• 故由 $\|\boldsymbol{A}\boldsymbol{x}-\boldsymbol{b}\|_{2}=\|\boldsymbol{\Sigma}\boldsymbol{y}-\boldsymbol{c}\|_{2}$ 可知必有 $\min _{\boldsymbol{x} \in \mathbb{C}^{n}}\|\boldsymbol{A} \boldsymbol{x}-\boldsymbol{b}\|_{2}=\min _{\boldsymbol{y} \in \mathbb{C}^{n}}\|\boldsymbol{\Sigma}\boldsymbol{y}-\boldsymbol{c}\|_{2}$.
• 记 $\boldsymbol{\Sigma}=\left[\begin{array}{cc}\mathrm{diag}\{\sigma_1,\ldots,\sigma_r\} & \boldsymbol{O}\\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right]$，进而
• $\boldsymbol{\Sigma}\boldsymbol{y}-\boldsymbol{c}=[\sigma_{1} y_{1}-c_{1} \;\; {\cdots} \;\; {\sigma_{r} y_{r}-c_{r}} \;\; {-c_{r+1}} \; {\cdots} \; {-c_{m}}]^{\mathrm{T}}$.
• 显然 $\sigma_{1} y_{1}-c_{1}=\cdots=\sigma_{r} y_{r}-c_{r}=0$ 时 $\|\boldsymbol{\Sigma}\boldsymbol{y}-\boldsymbol{c}\|_{2}$ 最小，进而由此解出 $y_{1}, y_{2}, \cdots, y_{r}$.
• 最后，由 $\boldsymbol{y}=\boldsymbol{V}^{\mathrm{\mathrm{H}}}\boldsymbol{x}$ ，得到 $\boldsymbol{x}=\boldsymbol{V}\boldsymbol{y}$，即为所求的最小二乘解.

---

数据压缩

矩阵 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$ 包含 $mn$ 个数据，可否使用尽可能少的数据来表示（或逼近） $\boldsymbol{A}$？

• 通常情况下，可以用 $\mathrm{rank} \boldsymbol{A}$ 来度量 $\boldsymbol{A}$ 中数据的冗余度 (Redundancy)
• 例 若 $\mathrm{rank} \boldsymbol{A}=1$，则必存在 $\boldsymbol{u} \in \mathbb{C}^{m}$ 和 $\boldsymbol{v} \in \mathbb{C}^{n}$，使得 $\boldsymbol{A}=\boldsymbol{u v}^{\mathrm{T}}$.
  
  • 上式意味着，用 $m+n$ 个独立的数据就能够完全表示 $\boldsymbol{A}$.

---

例 一幅图像可以对应于一个矩阵 $\boldsymbol{A}=[a_{ij}]_{m\times n}$，其中 $a_{ij}$ 表示坐标 $(i,j)$ 处的点的像素值（或灰度）.

• 设 $\boldsymbol{A}$ 的 SVD 为 $\boldsymbol{A}=\boldsymbol{U}\left[\begin{array}{cc}\boldsymbol{\Sigma} & \boldsymbol{O}\\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right] \boldsymbol{V}^{\mathrm{H}}=\sum_{i=1}^{r}\sigma_i\boldsymbol{u}_i\boldsymbol{v}_i^{\mathrm{H}}$.
• 记 $\boldsymbol{A}_{k}=\sum_{i=1}^{k}\sigma_i\boldsymbol{u}_i\boldsymbol{v}_i^{\mathrm{H}}\;\;(k\leq r)$, 不难发现，存储 $\boldsymbol{A}_k$ 只需要 $k(m+n+1)$ 个数据.
• 当图像尺寸特别大时，可以考虑用 $\boldsymbol{A}_k$ 来近似 $\boldsymbol{A}$，达到节省存储空间的目的.
• 此时图像 压缩比 可定义为 $C_{R}=\frac{m \times n}{(m+n+1) k}$.

---

潜在语义索引（Latent Semantic Indexing, LSI）[1]

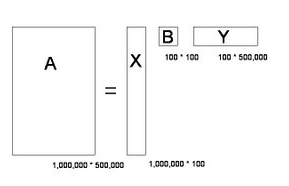
例 一百万篇文章和五十万个不同词汇的关联可以描述为一个 $1000000\times500000$ 的矩阵

• 如图 SVD 后，所需的存储量仅为原来的三千分之一.
• $\boldsymbol{X}$ 的每列对应一个主题，列中元素代表每篇文章与之的相关性.
• $\boldsymbol{Y}$ 的每行也对应与以上相同的某个主题，行中元素代表每个单词与之的相关性.
• $\boldsymbol{B}$ 的对角元代表主题的重要性.

---

以 $\mathrm{rank}\boldsymbol{A}=2$ 为例[2]

• 红点表示单词，蓝点表示文档.
• 通过 SVD 得到的关联性可以用来完成词和文档的聚类 (Clustering).
• 利用并行算法已可以高效地完成 SVD.

---

小结

• SVD
  
  • 奇异值的定义与性质
  • SVD 的求解
  • SVD 的应用

---

SVD[3]

---

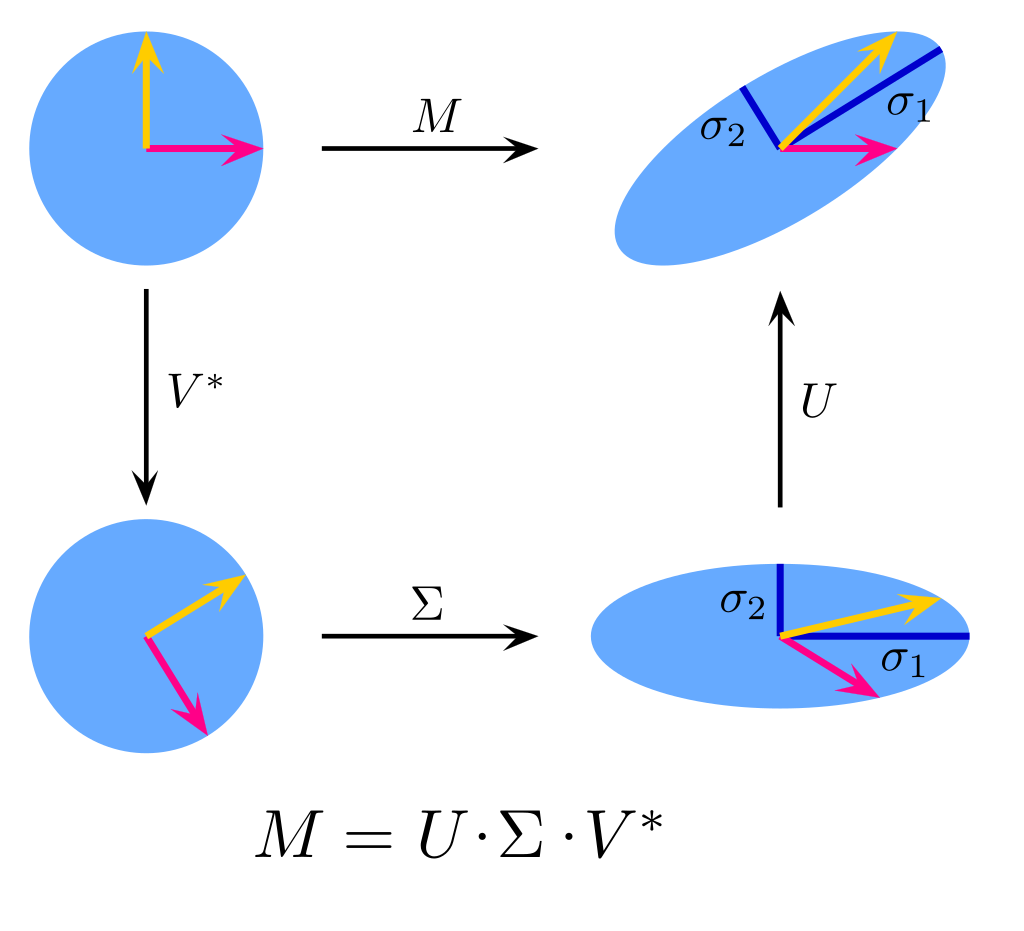
A brief history of SVD[4]

The singular value decomposition was originally developed by differential geometers, who wished to determine whether a real bilinear form could be made equal to another by independent orthogonal transformations of the two spaces it acts on. Eugenio Beltrami and Camille Jordan discovered independently, in 1873 and 1874 respectively, that the singular values of the bilinear forms, represented as a matrix, form a complete set of invariants for bilinear forms under orthogonal substitutions. James Joseph Sylvester also arrived at the singular value decomposition for real square matrices in 1889, apparently independently of both Beltrami and Jordan. Sylvester called the singular values the canonical multipliers of the matrix A. The fourth mathematician to discover the singular value decomposition independently is Autonne in 1915, who arrived at it via the polar decomposition. The first proof of the singular value decomposition for rectangular and complex matrices seems to be by Carl Eckart and Gale J. Young in 1936; they saw it as a generalization of the principal axis transformation for Hermitian matrices.

---

Practical methods for computing the SVD date back to Kogbetliantz in 1954, 1955 and Hestenes in 1958, resembling closely the Jacobi eigenvalue algorithm, which uses plane rotations or Givens rotations. However, these were replaced by the method of Gene Golub and William Kahan published in 1965, which uses Householder transformations or reflections. In 1970, Golub and Christian Reinsch published a variant of the Golub/Kahan algorithm[5] that is still the one most-used today.