5.1 矩阵的广义逆及其应用

高等工程数学 讲义 2021

---

---

5.1.1 广义逆的定义与性质

能否推广矩阵逆的概念，使得任何矩阵在某种意义下都可逆？

• 若 $\boldsymbol{F} \in \mathbb{C}^{m \times r}$ 列满秩，则 $\boldsymbol{F}$ 有左逆，$\boldsymbol{F}_{\mathrm{L}}^{-1}=\left(\boldsymbol{F}^{\mathrm{H}} \boldsymbol{F}\right)^{-1} \boldsymbol{F}^{\mathrm{H}}$.
• 若 $\boldsymbol{G} \in \mathbb{C}^{m \times r}$ 行满秩，则 $\boldsymbol{G}$ 有右逆 $\boldsymbol{G}_{\mathrm{R}}^{-1}=\boldsymbol{G}^{\mathrm{H}}\left(\boldsymbol{G} \boldsymbol{G}^{\mathrm{H}}\right)^{-1}$.
• 对于一般的矩阵 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$，有满秩分解 $\boldsymbol{A}=\boldsymbol{F}\boldsymbol{G}$，可否定义 $\boldsymbol{A}$ 的逆为 $\boldsymbol{G}_{\mathrm{R}}^{-1} \boldsymbol{F}_{\mathrm{L}}^{-1}$ ？

---

Moore-Penrose 广义逆

设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$ ，若存在矩阵 $\boldsymbol{G} \in \mathbb{C}^{n \times m}$ ，使得

1. $\boldsymbol{A} \boldsymbol{G} \boldsymbol{A}=\boldsymbol{A}$
2. ${\boldsymbol{G}} {\boldsymbol{A}} {\boldsymbol{G}}={\boldsymbol{G}}$
3. $(\boldsymbol{A} \boldsymbol{G})^{\mathrm{H}}=\boldsymbol{A} \boldsymbol{G}$
4. $({\boldsymbol{G}} {\boldsymbol{A}})^{\mathrm{H}}={\boldsymbol{G}} {\boldsymbol{A}}$

则称 $\boldsymbol{G}$ 为 $\boldsymbol{A}$ 的 Moore-Penrose广义逆（或 M-P广义逆，加号逆，Moore–Penrose Inverse），记为 $\boldsymbol{A}^+$ .

---

M-P 逆的性质 (1)

设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$ ，则 $\boldsymbol{A}$ 的 M-P逆存在且唯一.
1. 若 $\boldsymbol{F}$ 列满秩，则 $\bbox[lightgreen]{\boldsymbol{F}^{+}=\boldsymbol{F}_{\mathrm{L}}^{-1}=\left(\boldsymbol{F}^{\mathrm{H}} \boldsymbol{F}\right)^{-1} \boldsymbol{F}^{\mathrm{H}}}$
2. 若 $\boldsymbol{G}$ 行满秩，则 $\bbox[yellow]{\boldsymbol{G}^{+}=\boldsymbol{G}_{\mathrm{R}}^{-1}=\boldsymbol{G}^{\mathrm{H}}\left(\boldsymbol{G} \boldsymbol{G}^{\mathrm{H}}\right)^{-1}}$
3. 若 $\boldsymbol{A}$ 的满秩分解为 $\boldsymbol{A}=\bbox[lightgreen]{\boldsymbol{F}}\bbox[yellow]{\boldsymbol{G}}$, 则 $\boldsymbol{A}^{+}=\bbox[yellow]{\boldsymbol{G}^{+}}\bbox[lightgreen]{\boldsymbol{F}^{+}}=\bbox[yellow]{\boldsymbol{G}^{\mathrm{H}}\left(\boldsymbol{G} \boldsymbol{G}^{\mathrm{H}}\right)^{-1}}\bbox[lightgreen]{\left(\boldsymbol{F}^{\mathrm{H}} \boldsymbol{F}\right)^{-1} \boldsymbol{F}^{\mathrm{H}}}$

---

证明：

• 设 $\boldsymbol{G}_1,\boldsymbol{G}_2$ 均为 $\boldsymbol{A}$ 的 M-P 逆.
• $\boldsymbol{G}_2\boldsymbol{A}=\boldsymbol{G}_2\boldsymbol{A}\boldsymbol{G}_1\boldsymbol{A}=(\boldsymbol{G}_2\boldsymbol{A})^{\mathrm{H}}(\boldsymbol{G}_1\boldsymbol{A})^{\mathrm{H}}$
  
  • $=(\boldsymbol{G}_1\boldsymbol{A}\boldsymbol{G}_2\boldsymbol{A})^{\mathrm{H}}=(\boldsymbol{G}_1\boldsymbol{A})^{\mathrm{H}}=\boldsymbol{G}_1\boldsymbol{A}$.
• 同理可证 $\boldsymbol{A}\boldsymbol{G}_2=\boldsymbol{A}\boldsymbol{G}_1$.
• 于是 $\boldsymbol{G}_1=\boldsymbol{G}_1\boldsymbol{A}\boldsymbol{G}_1=\boldsymbol{G}_2\boldsymbol{A}\boldsymbol{G}_1=\boldsymbol{G}_2\boldsymbol{A}\boldsymbol{G}_2=\boldsymbol{G}_2$.

---

M-P 逆的性质 (2)

1. 若 $\boldsymbol{A}$ 为可逆的方阵，则 $\boldsymbol{A}^+=\boldsymbol{A}^{-1}$.
2. 若 $\boldsymbol{A}=\boldsymbol{O}$，则 $\boldsymbol{A}^{+}=\boldsymbol{A}^{\mathrm{T}}$.
3. $\left(\boldsymbol{A}^{+}\right)^{+}=\boldsymbol{A}$.
4. $(\lambda {\boldsymbol{A}})^{+}={\boldsymbol{A}}^{+} / \lambda \;\;(\lambda \neq 0)$.
5. $\left(\boldsymbol{A}^{+}\right)^{\mathrm{T}}=\left(\boldsymbol{A}^{\mathrm{T}}\right)^{+}$.
6. $\left(\boldsymbol{A}^{+}\right)^{\mathrm{H}}=\left(\boldsymbol{A}^{\mathrm{H}}\right)^{+}$.

---

M-P 逆的性质 (3)

1. 若 $\boldsymbol{F}$ 列满秩，则 $(\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F})^+=\boldsymbol{F}^+(\boldsymbol{F}^+)^{\mathrm{H}}$.
2. 若 $\boldsymbol{G}$ 行满秩，则 $(\boldsymbol{G}\boldsymbol{G}^{\mathrm{H}})^+=(\boldsymbol{G}^+)^{\mathrm{H}}\boldsymbol{G}^+$.
3. 对任意 $\boldsymbol{A}\in\mathbb{C}^{m\times n}$,
   
   • $(\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A})^+=\boldsymbol{A}^+(\boldsymbol{A}^+)^{\mathrm{H}}=\boldsymbol{A}^+(\boldsymbol{A}^{\mathrm{H}})^+$.
   • $(\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}})^+=(\boldsymbol{A}^+)^{\mathrm{H}}\boldsymbol{A}^+=(\boldsymbol{A}^{\mathrm{H}})^+\boldsymbol{A}^+$.

---

提示： 证明：若 $\boldsymbol{F}$ 列满秩，则 $(\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F})^+=\boldsymbol{F}^+(\boldsymbol{F}^+)^{\mathrm{H}}$

• $\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F}\boldsymbol{F}^+(\boldsymbol{F}^+)^{\mathrm{H}}\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F}=\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F}\boldsymbol{F}^+(\boldsymbol{F}\boldsymbol{F}^+)^{\mathrm{H}}\boldsymbol{F}$
  
  • $=\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F}\boldsymbol{F}^+\boldsymbol{F}\boldsymbol{F}^+\boldsymbol{F}=\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F}$
• $\boldsymbol{F}^+(\boldsymbol{F}^+)^{\mathrm{H}}\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F}\boldsymbol{F}^+(\boldsymbol{F}^+)^{\mathrm{H}}=\boldsymbol{F}^+(\boldsymbol{F}\boldsymbol{F}^+)^{\mathrm{H}}\boldsymbol{F}\boldsymbol{F}^+(\boldsymbol{F}^+)^{\mathrm{H}}$
  
  • $=\boldsymbol{F}^+\boldsymbol{F}\boldsymbol{F}^+\boldsymbol{F}\boldsymbol{F}^+(\boldsymbol{F}^+)^{\mathrm{H}}=\boldsymbol{F}^+(\boldsymbol{F}^+)^{\mathrm{H}}$
• $\left(\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F}\boldsymbol{F}^+(\boldsymbol{F}^+)^{\mathrm{H}}\right)^{\mathrm{H}}=\boldsymbol{F}^+(\boldsymbol{F}^+)^{\mathrm{H}}\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F}=\boldsymbol{F}^+(\boldsymbol{F}\boldsymbol{F}^+)^{\mathrm{H}}\boldsymbol{F}$
  
  • $=\boldsymbol{F}^+\boldsymbol{F}\boldsymbol{F}^+\boldsymbol{F}=\boldsymbol{F}^+\boldsymbol{F}=\boldsymbol{F}_L^{-1}\boldsymbol{F}=\boldsymbol{I}=\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F}\boldsymbol{F}^+(\boldsymbol{F}^+)^{\mathrm{H}}$
• $\left(\boldsymbol{F}^+(\boldsymbol{F}^+)^{\mathrm{H}}\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F}\right)^{\mathrm{H}}=\left(\boldsymbol{F}^+(\boldsymbol{F}\boldsymbol{F}^+)^{\mathrm{H}}\boldsymbol{F}\right)^{\mathrm{H}}=(\boldsymbol{F}^+\boldsymbol{F}\boldsymbol{F}^+\boldsymbol{F})^{\mathrm{H}}$
  
  • $=(\boldsymbol{F}^+\boldsymbol{F})^{\mathrm{H}}=\boldsymbol{I}=\boldsymbol{F}^+(\boldsymbol{F}^+)^{\mathrm{H}}\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F}$

---

对于任意的 $\boldsymbol{A}\in\mathbb{C}^{m\times n}$，设 $\boldsymbol{A}$ 的满秩分解为 $\boldsymbol{A}=\boldsymbol{F}\boldsymbol{G}$

• $(\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A})^+=(\boldsymbol{G}^{\mathrm{H}}\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F}\boldsymbol{G})^+=\boldsymbol{G}^+(\boldsymbol{G}^{\mathrm{H}}\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F})^+$
  
  • $=\boldsymbol{G}^+(\boldsymbol{F}^{\mathrm{H}}\boldsymbol{F})^+(\boldsymbol{G}^{\mathrm{H}})^+=\boldsymbol{G}^+\boldsymbol{F}^+(\boldsymbol{F}^{\mathrm{H}})^+(\boldsymbol{G}^+)^{\mathrm{H}}$
  • $=\boldsymbol{G}^+\boldsymbol{F}^+(\boldsymbol{F}^+)^{\mathrm{H}}(\boldsymbol{G}^+)^{\mathrm{H}}=\boldsymbol{A}^+(\boldsymbol{G}^+\boldsymbol{F}^+)^{\mathrm{H}}$
  • $=\boldsymbol{A}^+(\boldsymbol{A}^+)^{\mathrm{H}}$

---

M-P 逆的性质 (4)

1. $\boldsymbol{A}^{\mathrm{H}}=\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A} \boldsymbol{A}^{+}=\boldsymbol{A}^{+} \boldsymbol{A} \boldsymbol{A}^{\mathrm{H}}$.
2. $\boldsymbol{A}^{+}=\left(\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}\right)^{+} \boldsymbol{A}^{\mathrm{H}}=\boldsymbol{A}^{\mathrm{H}}\left(\boldsymbol{A} \boldsymbol{A}^{\mathrm{H}}\right)^{+}$.
3. 若 $\boldsymbol{U}^{\mathrm{H}}\boldsymbol{U}=\boldsymbol{I}$ 或 $\boldsymbol{U}\boldsymbol{U}^{\mathrm{H}}=\boldsymbol{I}$，则 $\boldsymbol{U}^+=\boldsymbol{U}^{\mathrm{H}}$.
   
   • 注意：以上的 $\boldsymbol{U}$ 不一定是酉矩阵.

---

提示：

• $\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{A}^+=\boldsymbol{A}^{\mathrm{H}}(\boldsymbol{A}\boldsymbol{A}^+)^{\mathrm{H}}=\boldsymbol{A}^{\mathrm{H}}(\boldsymbol{A}^{\mathrm{H}})^+\boldsymbol{A}^{\mathrm{H}}=\boldsymbol{A}^{\mathrm{H}}$
• $(\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A})^+\boldsymbol{A}^{\mathrm{H}}=\boldsymbol{A}^+(\boldsymbol{A}^+)^{\mathrm{H}}\boldsymbol{A}^{\mathrm{H}}=\boldsymbol{A}^+(\boldsymbol{A}\boldsymbol{A}^+)^{\mathrm{H}}$
  
  • $=\boldsymbol{A}^+\boldsymbol{A}\boldsymbol{A}^+=\boldsymbol{A}^+$.
• 若 $\boldsymbol{U}^{\mathrm{H}}\boldsymbol{U}=\boldsymbol{I}$，则
  
  • $\boldsymbol{U}^+=(\boldsymbol{U}^{\mathrm{H}}\boldsymbol{U})^+\boldsymbol{U}^{\mathrm{H}}=\boldsymbol{I}^+\boldsymbol{U}^{\mathrm{H}}=\boldsymbol{I}\boldsymbol{U}^{\mathrm{H}}=\boldsymbol{U}^{\mathrm{H}}$.

---

M-P 逆的性质 (5)

若 $\boldsymbol{U},\boldsymbol{\boldsymbol{V}}$ 均为酉矩阵，则 $({\boldsymbol{U}} {\boldsymbol{A}} {\boldsymbol{\boldsymbol{V}}})^{+}={\boldsymbol{\boldsymbol{V}}}^{\mathrm{H}} {\boldsymbol{A}}^{+} {\boldsymbol{U}}^{\mathrm{H}}$.

• 提示： 设 $\boldsymbol{A}$ 的满秩分解为 $\boldsymbol{A}=\boldsymbol{F}\boldsymbol{G}$.
• 注意到 $\boldsymbol{UF}$ 和 $\boldsymbol{GV}$ 分别行满秩和列满秩，故
• $(\boldsymbol{U}\boldsymbol{A}\boldsymbol{\boldsymbol{V}})^+=(\boldsymbol{U}\boldsymbol{F}\boldsymbol{G}\boldsymbol{\boldsymbol{V}})^+=(\boldsymbol{G}\boldsymbol{\boldsymbol{V}})^+(\boldsymbol{U}\boldsymbol{F})^+$.
• $(\boldsymbol{G}\boldsymbol{\boldsymbol{V}})^+=(\boldsymbol{G}\boldsymbol{\boldsymbol{V}})_{\mathrm{R}}^{-1}=(\boldsymbol{G}\boldsymbol{\boldsymbol{V}})^{\mathrm{H}}(\boldsymbol{G}\boldsymbol{\boldsymbol{V}}(\boldsymbol{G}\boldsymbol{\boldsymbol{V}})^{\mathrm{H}})^{-1}$
  
  • $=\boldsymbol{\boldsymbol{V}}^{\mathrm{H}}\boldsymbol{G}^{\mathrm{H}}(\boldsymbol{G}\boldsymbol{\boldsymbol{V}}\boldsymbol{\boldsymbol{V}}^{\mathrm{H}}\boldsymbol{G}^{\mathrm{H}})^{-1}=\boldsymbol{\boldsymbol{V}}^{\mathrm{H}}\boldsymbol{G}^{\mathrm{H}}(\boldsymbol{G}\boldsymbol{G}^{\mathrm{H}})^{-1}=\boldsymbol{\boldsymbol{V}}^{\mathrm{H}}\boldsymbol{G}^+$.
• 同理 $(\boldsymbol{U}\boldsymbol{F})^+=\boldsymbol{F}^+\boldsymbol{U}^{\mathrm{H}}$.
• $(\boldsymbol{G}\boldsymbol{\boldsymbol{V}})^+(\boldsymbol{U}\boldsymbol{F})^+=\boldsymbol{\boldsymbol{V}}^{\mathrm{H}}\boldsymbol{G}^+\boldsymbol{F}^+\boldsymbol{U}^{\mathrm{H}}=\boldsymbol{\boldsymbol{V}}^{\mathrm{H}}\boldsymbol{A}^+\boldsymbol{U}^{\mathrm{H}}$.

---

M-P 逆的性质 (6)

$$\operatorname{rank} (\boldsymbol{A})=\operatorname{rank} (\boldsymbol{A}^{+})=\operatorname{rank} (\boldsymbol{A}^{+} \boldsymbol{A})=\operatorname{rank} (\boldsymbol{A} \boldsymbol{A}^{+})$$

• 提示：
  
  • $\mathrm{rank}(\boldsymbol{A})=\mathrm{rank}(\boldsymbol{A}\boldsymbol{A}^+\boldsymbol{A})$
    
    • $\leq\mathrm{rank}(\boldsymbol{A}^+\boldsymbol{A})\leq\mathrm{rank}(\boldsymbol{A})$.
  • $\mathrm{rank}(\boldsymbol{A})=\mathrm{rank}(\boldsymbol{A}\boldsymbol{A}^+\boldsymbol{A})\leq\mathrm{rank}(\boldsymbol{A}^+)$.
  • $\mathrm{rank}(\boldsymbol{A}^+)=\mathrm{rank}(\boldsymbol{A}^+\boldsymbol{A}\boldsymbol{A}^+)\leq\mathrm{rank}(\boldsymbol{A})$.

---

M-P 逆的性质 (7)

1. $\boldsymbol{A}^+\boldsymbol{A}$，$\boldsymbol{A}\boldsymbol{A}^+$，$\boldsymbol{I}_{m}-\boldsymbol{A} \boldsymbol{A}^{+}$ 和 $\boldsymbol{I}_{n}-\boldsymbol{A}^{+} \boldsymbol{A}$ 均为幂等矩阵.
   
   • 注：$\boldsymbol{P}^2=\boldsymbol{P}$，则称 $\boldsymbol{P}$ 为 幂等矩阵 (Idempotent Matrix)
   • 幂等矩阵的特征值均为 $1$ 或 $0$.
   • $\mathrm{tr}(\boldsymbol{P})=\mathrm{rank}(\boldsymbol{P})$.
   • $\boldsymbol{P}$ 为幂等阵，当且仅当 $\boldsymbol{I}-\boldsymbol{P}$ 为幂等阵.
2. $m-\operatorname{rank}\left(\boldsymbol{I}_{m}-\boldsymbol{A} \boldsymbol{A}^{+}\right)=n-\operatorname{rank}\left(\boldsymbol{I}_{n}-\boldsymbol{A}^{+} \boldsymbol{A}\right)=\operatorname{rank} \boldsymbol{A}$.
   
   • 提示：$\mathrm{rank}(\boldsymbol{I}_{m}-\boldsymbol{A} \boldsymbol{A}^{+})=\mathrm{tr}(\boldsymbol{I}_{m}-\boldsymbol{A} \boldsymbol{A}^{+})$
     
     • $=\mathrm{tr}(\boldsymbol{I}_m)-\mathrm{tr}(\boldsymbol{A}\boldsymbol{A}^+)$
     • $=m-\mathrm{rank}(\boldsymbol{A}\boldsymbol{A}^+)=m-\mathrm{rank}(\boldsymbol{A})$.

---

注： 一般来说，$(\boldsymbol{A}\boldsymbol{B})^+$ 不等于 $\boldsymbol{B}^+\boldsymbol{A}^+$ 或 $\boldsymbol{A}^+\boldsymbol{B}^+$.

• 例 $\boldsymbol{A}=\left[\begin{array}{cc}1 & 1 \\ 0 & 0\end{array}\right]$，$\boldsymbol{B}=\left[\begin{array}{cc}0 & 0 \\ 1 & 1\end{array}\right]$.
  
  • $\boldsymbol{A}^+=\frac{1}{2}\left[\begin{array}{cc}1 & 0 \\ 1 & 0\end{array}\right]$，$\boldsymbol{B}^+=\frac{1}{2}\left[\begin{array}{cc}0 & 1 \\ 0 & 1\end{array}\right]$.
  • $(\boldsymbol{A}\boldsymbol{B})^+=\left[\begin{array}{cc}1 & 1 \\ 0 & 0\end{array}\right]^+=\frac{1}{2}\left[\begin{array}{cc}1 & 0 \\ 1 & 0\end{array}\right]$.
  • $\boldsymbol{B}^+\boldsymbol{A}^+=\frac{1}{4}\left[\begin{array}{cc}1 & 0 \\ 1 & 0\end{array}\right]\ne (\boldsymbol{A}\boldsymbol{B})^+$.
  • $\boldsymbol{A}^+\boldsymbol{B}^+=\frac{1}{4}\left[\begin{array}{cc}0 & 1 \\ 0 & 1\end{array}\right]\ne (\boldsymbol{A}\boldsymbol{B})^+$.

---

5.1.2 广义逆的计算

1. 满秩分解法
2. 奇异值分解法

---

满秩分解法

1. 先求 $\boldsymbol{A}$ 的满秩分解： $\boldsymbol{A}=\boldsymbol{F}\boldsymbol{G}$.
2. 再计算 $\boldsymbol{F}$ 的左逆和 $\boldsymbol{G}$ 的右逆，
   
   • $\boldsymbol{F}^{+}=\boldsymbol{F}_{\mathrm{L}}^{-1}=\left(\boldsymbol{F}^{\mathrm{H}} \boldsymbol{F}\right)^{-1} \boldsymbol{F}^{\mathrm{H}}$.
   • $\boldsymbol{G}^{+}=\boldsymbol{G}_{\mathrm{R}}^{-1}=\boldsymbol{G}^{\mathrm{H}}\left(\boldsymbol{G} \boldsymbol{G}^{\mathrm{H}}\right)^{-1}$.
3. $\boldsymbol{A}^{+}=(\boldsymbol{F}\boldsymbol{G})^+=\boldsymbol{G}^{+} \boldsymbol{F}^{+}=\boldsymbol{G}_{\mathrm{R}}^{-1} \boldsymbol{F}_{\mathrm{L}}^{-1}$.

---

例 $\boldsymbol{A}=\left[\begin{array}{rr}{1} & {-1} \\ {0} & {0}\end{array}\right]$，$\boldsymbol{B}=\left[\begin{array}{ll}{1} & {0} \\ {0} & {0}\end{array}\right]$ ，试求 $\boldsymbol{A}^+$，$\boldsymbol{B}^+$ 和 $(\boldsymbol{A}\boldsymbol{B})^+$.

---

提示

• $\boldsymbol{A}=\left[\begin{array}{rr}{1} & {-1} \\ {0} & {0}\end{array}\right]=\left[\begin{array}{l}{1} \\ {0}\end{array}\right]\left[\begin{array}{ll}{1} & {-1}\end{array}\right]=\boldsymbol{F} \boldsymbol{G}$.
• $\boldsymbol{F}^{+}=\boldsymbol{F}_L^{-1}=\left(\boldsymbol{F}^{\mathrm{H}} \boldsymbol{F}\right)^{-1} \boldsymbol{F}^{\mathrm{H}}=\left[\begin{array}{ll}{1} & {0}\end{array}\right]$.
• $\boldsymbol{G}^{+}=\boldsymbol{G}_R^{-1}=\boldsymbol{G}^{\mathrm{H}}\left(\boldsymbol{G} \boldsymbol{G}^{\mathrm{H}}\right)^{-1}=\frac{1}{2}\left[\begin{array}{r}{1} \\ {-1}\end{array}\right]$.
• $\boldsymbol{A}^{+}=\boldsymbol{G}^{+} \boldsymbol{F}^{+}=\frac{1}{2}\left[\begin{array}{r}{1} \\ {-1}\end{array}\right]\left[\begin{array}{ll}{1} & {0}\end{array}\right]=\frac{1}{2}\left[\begin{array}{rr}{1} & {0} \\ {-1} & {0}\end{array}\right]$.
• $\boldsymbol{B}^{+}=\left[\begin{array}{ll}{1} & {0} \\ {0} & {0}\end{array}\right]$.

---

注： 若

$$\boldsymbol{A}=\mathrm{diag}\{1,...,1,0,...,0\},$$

• 注意到 $\boldsymbol{A}^2=\boldsymbol{A}$ 且 $\boldsymbol{A}^{\mathrm{H}}=\boldsymbol{A}$,
• 故 $\boldsymbol{A}\boldsymbol{A}\boldsymbol{A}=\boldsymbol{A}$ 且 $(\boldsymbol{A}\boldsymbol{A})^{\mathrm{H}}=\boldsymbol{A}^{\mathrm{H}}=\boldsymbol{A}$.
• 令 $\boldsymbol{G}=\boldsymbol{A}$，可以验证 $\boldsymbol{G}$ 满足 M-P 逆的定义,
• 故 $\boldsymbol{A}^+=\boldsymbol{G}=\boldsymbol{A}$.

---

例 $\boldsymbol{A}=\left[\begin{array}{lll}{1} & {2} & {0} \\ {0} & {0} & {1} \\ {2} & {4} & {0}\end{array}\right]$ ，求 $\boldsymbol{A}^+$ .

• 解： $\boldsymbol{A}$ 的Hermite标准形 $\left[\begin{array}{lll}{1} & {2} & {0} \\ {0} & {0} & {1} \\ {0} & {0} & {0}\end{array}\right]$.
• $\boldsymbol{A}$ 的满秩分解 $\boldsymbol{A}=\left[\begin{array}{ll}{1} & {0} \\ {0} & {1} \\ {2} & {0}\end{array}\right]\left[\begin{array}{lll}{1} & {2} & {0} \\ {0} & {0} & {1}\end{array}\right]=\boldsymbol{F} \boldsymbol{G}$.
• $\boldsymbol{F}^{\mathrm{H}} \boldsymbol{F}=\left[\begin{array}{lll}{1} & {0} & {2} \\ {0} & {1} & {0}\end{array}\right]\left[\begin{array}{ll}{1} & {0} \\ {0} & {1} \\ {2} & {0}\end{array}\right]=\left[\begin{array}{ll}{5} & {0} \\ {0} & {1}\end{array}\right]$.
• $\left(\boldsymbol{F}^{\mathrm{H}} \boldsymbol{F}\right)^{-1}=\frac{1}{5}\left[\begin{array}{ll}{1} & {0} \\ {0} & {5}\end{array}\right]$.

---

• $\boldsymbol{G} \boldsymbol{G}^{\mathrm{H}}=\left[\begin{array}{lll}{1} & {2} & {0} \\ {0} & {0} & {1}\end{array}\right]\left[\begin{array}{ll}{1} & {0} \\ {2} & {0} \\ {0} & {1}\end{array}\right]=\left[\begin{array}{ll}{5} & {0} \\ {0} & {1}\end{array}\right]$.
• $\left(\boldsymbol{G} \boldsymbol{G}^{\mathrm{H}}\right)^{-1}=\frac{1}{5}\left[\begin{array}{ll}{1} & {0} \\ {0} & {5}\end{array}\right]$.
• $\boldsymbol{F}^{+}=\left(\boldsymbol{F}^{\mathrm{H}} \boldsymbol{F}\right)^{-1} \boldsymbol{F}^{\mathrm{H}}=\frac{1}{5}\left[\begin{array}{cc}{1} & {0} \\ {0} & {5}\end{array}\right]\left[\begin{array}{ccc}{1} & {0} & {2} \\ {0} & {1} & {0}\end{array}\right]=\frac{1}{5}\left[\begin{array}{ccc}{1} & {0} & {2} \\ {0} & {5} & {0}\end{array}\right]$.
• $\boldsymbol{G}^{+}=\boldsymbol{G}^{\mathrm{H}}\left(\boldsymbol{G} \boldsymbol{G}^{\mathrm{H}}\right)^{-1}=\left[\begin{array}{cc}{1} & {0} \\ {2} & {0} \\ {0} & {1}\end{array}\right] \frac{1}{5}\left[\begin{array}{cc}{1} & {0} \\ {0} & {5}\end{array}\right]=\frac{1}{5}\left[\begin{array}{cc}{1} & {0} \\ {2} & {0} \\ {0} & {5}\end{array}\right]$.
• $\boldsymbol{A}^{+}=\boldsymbol{G}^{+} \boldsymbol{F}^{+}=\frac{1}{5}\left[\begin{array}{cc}{1} & {0} \\ {2} & {0} \\ {0} & {5}\end{array}\right] \frac{1}{5}\left[\begin{array}{ccc}{1} & {0} & {2} \\ {0} & {5} & {0}\end{array}\right]=\frac{1}{25}\left[\begin{array}{ccc}{1} & {0} & {2} \\ {2} & {0} & {4} \\ {0} & {25} & {0}\end{array}\right]$.

---

例 设 $\boldsymbol{\Sigma}=\mathrm{diag}\{\sigma_1,\sigma_2,\ldots,\sigma_r\}$ 可逆，

$$\boldsymbol{A}=\left[\begin{array}{c}\boldsymbol{\Sigma} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right]_{m\times n}$$

求 $\boldsymbol{A}^+$ .

• 提示：令 $\boldsymbol{G}=\left[\begin{array}{c}\boldsymbol{\Sigma}^{-1} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right]_{n\times m}$.
• 验证 $\boldsymbol{A} \boldsymbol{G}=\left[\begin{array}{ll}{\boldsymbol{I}_{r}} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right]_{m \times m}$ ， $\boldsymbol{G} \boldsymbol{A}=\left[\begin{array}{ll}{\boldsymbol{I}_{r}} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right]_{n \times n}$
• 进而易知 $\boldsymbol{A}^+=\boldsymbol{G}$.

---

奇异值分解法

1. 设 $\boldsymbol{A}$ 的奇异值分解 $\boldsymbol{A}=\boldsymbol{U}\left[\begin{array}{ccc}{\boldsymbol{\Sigma}} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right] \boldsymbol{V}^{\mathrm{H}}$,
   
   • 其中 $\boldsymbol{\Sigma}=\mathrm{diag}\{\sigma_1,\ldots,\sigma_r\}$,
   • $\sigma_1,\ldots,\sigma_n$ 为 $\boldsymbol{A}$ 的正奇异值.
2. 由 M-P 逆的性质 $\boldsymbol{A}^{+}=\boldsymbol{V}\left[\begin{array}{ll}{\boldsymbol{\Sigma}^{-1}} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O}\end{array}\right] \boldsymbol{U}^{\mathrm{H}}$.

---

例 已知 $\boldsymbol{A}=\left[\begin{array}{ll}{2} & {1} \\ {0} & {2} \\ {1} & {0}\end{array}\right]$ 的奇异值分解

$$\left[\begin{array}{ccc}{\frac{3}{\sqrt{14}}} & {\frac{1}{\sqrt{6}}} & {\frac{2}{\sqrt{21}}} \\ {\frac{2}{\sqrt{14}}} & {-\frac{2}{\sqrt{6}}} & {-\frac{1}{\sqrt{21}}} \\ {\frac{1}{\sqrt{14}}} & {\frac{1}{\sqrt{6}}} & {-\frac{4}{\sqrt{21}}}\end{array}\right]\left[\begin{array}{cc}{\sqrt{7}} & {0} \\ {0} & {\sqrt{3}} \\ {0} & {0}\end{array}\right]\left[\begin{array}{cc}{\frac{1}{\sqrt{2}}} & {\frac{1}{\sqrt{2}}} \\ {\frac{1}{\sqrt{2}}} & {-\frac{1}{\sqrt{2}}}\end{array}\right],$$

• 则 $\boldsymbol{A}^+=\left[\begin{array}{cc}{\frac{1}{\sqrt{2}}} & {\frac{1}{\sqrt{2}}} \\ {\frac{1}{\sqrt{2}}} & {-\frac{1}{\sqrt{2}}}\end{array}\right]\left[\begin{array}{ccc} \frac{1}{\sqrt{7}} & {0} & 0\\ {0} & \frac{1}{\sqrt{3}} & {0}\end{array}\right]\left[\begin{array}{ccc}{\frac{3}{\sqrt{14}}} & {\frac{2}{\sqrt{14}}} & {\frac{1}{\sqrt{14}}} \\ {\frac{1}{\sqrt{6}}} & {-\frac{2}{\sqrt{6}}} & {\frac{1}{\sqrt{6}}} \\ {\frac{2}{\sqrt{21}}} & -{\frac{1}{\sqrt{21}}} & {-\frac{4}{\sqrt{21}}}\end{array}\right].$

---

5.2 广义逆在解线性方程组中的应用

设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$ ， $\boldsymbol{x}\in\mathbb{C}^n$ ， $\boldsymbol{b}\in\mathbb{C}^m$ ，若方程组

$$\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$$

有解，则称该方程组是 相容的 (Consistent/Compatible). 否则称之为 不相容的.

---

定理 设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$，$\boldsymbol{x}\in\mathbb{C}^n$，$\boldsymbol{b}\in\mathbb{C}^m$，若方程组 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 是相容的，则其通解为

$$\boldsymbol{x}=\boldsymbol{A}^{+}\boldsymbol{b}+\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right)\boldsymbol{t} \quad\left(\forall \boldsymbol{t} \in \mathbb{C}^{n}\right).$$

---

提示：先证对任意 $\boldsymbol{t} \in \mathbb{C}^{n}$ ，

$\boldsymbol{x}=\boldsymbol{A}^{+} \boldsymbol{b}+\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{t}$

都是 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的解.

• 因为 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 相容，故存在 $\boldsymbol{x}_0$ ，使得 $\boldsymbol{A}\boldsymbol{x}_0=\boldsymbol{b}$.
• $\boldsymbol{A}\left(\boldsymbol{A}^{+} \boldsymbol{b}+\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{t}\right)$
  
  • $=\boldsymbol{A} \boldsymbol{A}^{+} \boldsymbol{b}+\left(\boldsymbol{A}-\boldsymbol{A} \boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{t}$
  • $=\boldsymbol{A} \boldsymbol{A}^{+} \boldsymbol{A} \boldsymbol{x}_{0}=\boldsymbol{A} \boldsymbol{x}_{0}=\boldsymbol{b}$.

---

再证若 $\boldsymbol{x}_0$ 是 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的解，则存在 $\boldsymbol{t}\in\mathbb{C}^n$ ，使得

$$\boldsymbol{x}_{0}=\boldsymbol{A}^{+} \boldsymbol{b}+\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{t}.$$

• 取 $\boldsymbol{t}=\boldsymbol{x}_0$, 则
• $\boldsymbol{A}^{+} \boldsymbol{b}+\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{t}=\boldsymbol{A}^{+} \boldsymbol{b}+\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{x}_{0}$
  
  • $=\boldsymbol{A}^{+} \boldsymbol{b}+\boldsymbol{x}_{0}-\boldsymbol{A}^{+} \boldsymbol{A} \boldsymbol{x}_{0}$
  • $=\boldsymbol{A}^{+} \boldsymbol{b}+\boldsymbol{x}_{0}-\boldsymbol{A}^{+} \boldsymbol{b}=\boldsymbol{x}_0.$

---

注:

• 由第一部分的证明可知 $\boldsymbol{A}^+\boldsymbol{b}$ 是 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的特解.
• 由定理可知 $\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{t} \quad\left(\forall \boldsymbol{t} \in \mathbb{C}^{n}\right)$ 是齐次方程组 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}$ 的通解.
• 根据 非齐次线性方程组解的结构 性质：
  
  • $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的通解可表示为 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}$ 的通解加上 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的一个特解.

---

例 求解线性方程组

$$\left\{\begin{array}{l}{x_{1}+2 x_{3}=1} \\ {2 x_{1}+x_{2}+4 x_{3}=2}\end{array}\right.$$

---

提示

• 记 $\boldsymbol{A}=\left[\begin{array}{lll}{1} & {0} & {2} \\ {2} & {1} & {4}\end{array}\right]$ ， $\boldsymbol{x}=\left[\begin{array}{l}{x_{1}} \\ {x_{2}} \\ {x_{3}}\end{array}\right]$ ， $\boldsymbol{b}=\left[\begin{array}{l}{1} \\ {2}\end{array}\right]$.
• 因为 $\boldsymbol{A}$ 行满秩, 故
  
  • $\boldsymbol{A}^{+}=\left[\begin{array}{ll}{1} & {2} \\ {0} & {1} \\ {2} & {4}\end{array}\right]\left(\left[\begin{array}{lll}{1} & {0} & {2} \\ {2} & {1} & {4}\end{array}\right]\left[\begin{array}{ll}{1} & {2} \\ {0} & {1} \\ {2} & {4}\end{array}\right]\right)^{-1}=\frac{1}{5}\left[\begin{array}{rr}{1} & {0} \\ {-10} & {5} \\ {2} & {0}\end{array}\right]$.
• $\boldsymbol{A}^{+} \boldsymbol{A}=\frac{1}{5}\left[\begin{array}{rr}{1} & {0} \\ {-10} & {5} \\ {2} & {0}\end{array}\right]\left[\begin{array}{lll}{1} & {0} & {2} \\ {2} & {1} & {4}\end{array}\right]=\frac{1}{5}\left[\begin{array}{ccc}{1} & {0} & {2} \\ {0} & {5} & {0} \\ {2} & {0} & {4}\end{array}\right]$.
• $\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}=\frac{1}{5}\left[\begin{array}{ccc}{4} & {0} & {-2} \\ {0} & {0} & {0} \\ {-2} & {0} & {1}\end{array}\right]$.

---

• $\boldsymbol{A}^{+}\boldsymbol{b}=\frac{1}{5}\left[\begin{array}{rr}{1} & {0} \\ {-10} & {5} \\ {2} & {0}\end{array}\right]\left[\begin{array}{l}{1} \\ {2}\end{array}\right]=\frac{1}{5}\left[\begin{array}{l}{1} \\ {0} \\ {2}\end{array}\right]$.
• 所求通解
• $\boldsymbol{x}=\boldsymbol{A}^{+}\boldsymbol{b}+\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right)\boldsymbol{t}$
  
  • $=\frac{1}{5}\left[\begin{array}{c}{1} \\ {0} \\ {2}\end{array}\right]+\frac{1}{5}\left[\begin{array}{ccc}{4} & {0} & {-2} \\ {0} & {0} & {0} \\ {-2} & {0} & {1}\end{array}\right]\left[\begin{array}{c}{t_{1}} \\ {t_{2}} \\ {t_{3}}\end{array}\right]$
  • $=\frac{1}{5}\left[\begin{array}{c}{1} \\ {0} \\ {2}\end{array}\right]+\frac{1}{5}\left[\begin{array}{c}{-2\left(-2 t_{1}+t_{3}\right)} \\ {0} \\ {-2 t_{1}+t_{3}}\end{array}\right]=\frac{1}{5}\left[\begin{array}{l}{1} \\ {0} \\ {2}\end{array}\right]+c\left[\begin{array}{c}{-2} \\ {0} \\ {1}\end{array}\right],$
  • $(c\in\mathbb{C})$.

---

5.2.1 广义逆在最小二乘问题中的应用

• 假设有一个线性系统 $L$,
  
  • 每次输入一个向量 $\boldsymbol{a}_{i}=\left[a_{i 1}, a_{i 2}, \cdots, a_{i n}\right]$,
  • 对应的输出为线性组合 $y_{i}=x_{1} a_{i 1}+x_{2} a_{i 2}+\cdots+x_{n} a_{i n}$.
  • $L$ 的行为完全由系统参数 $\boldsymbol{x}=[x_1\;\;x_2\;...\;x_n]^{\mathrm{T}}$ 决定.
• 为了求得系统参数，重复进行 $m$ 次试验，记录系统的输入和输出.
  
  • 输入：$\boldsymbol{A}=[\boldsymbol{a}_1^{\mathrm{T}}\;\;\boldsymbol{a}_2^{\mathrm{T}}\;...\;\boldsymbol{a}_m^{\mathrm{T}}]^{\mathrm{T}}$,
  • 测量到的输出： $\boldsymbol{b}=[b_1\;\;b_2\;...\;b_m]^{\mathrm{T}}$.
• 理论上 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 是相容的, 但由于存在观测误差，实际观测到的 $\boldsymbol{b}$ 并不等于真实的输出 $\boldsymbol{y}$.

---

最小二乘问题

• 问题： 如何/可否根据 $\boldsymbol{A}, \boldsymbol{b}$ 尽可能精确地推算出线性系统 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{y}$ 的参数 $\boldsymbol{x}$？
• 等价说法：对不相容的方程组，能否拓广解的概念，使其“有解”？这样的解有何意义？
• 数学描述：已知 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$，$\boldsymbol{b}\in \mathbb{C}^{m}$，求 $\boldsymbol{x}^{*} \in \mathbb{C}^{n}$，使得 $\left\|\boldsymbol{A} \boldsymbol{x}^{*}-\boldsymbol{b}\right\|_{2}=\min _{\boldsymbol{x} \in \mathbb{C}^{n}}\|\boldsymbol{A} \boldsymbol{x}-\boldsymbol{b}\|_{2}$.
• 如果以上的 $\boldsymbol{x}^*$ 存在，则称其为是方程组 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的 最小二乘解 (Least-Squares Solution)

---

分析

• 记 $\boldsymbol{A}=[\boldsymbol{A}_1\;\;\boldsymbol{A}_2\;...\;\boldsymbol{A}_n]$.
  
  1. 若 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 是相容的，则 $\boldsymbol{b}\in \mathscr{R}(\boldsymbol{A})=\mathrm{span}\{\boldsymbol{A}_1,\boldsymbol{A}_2,\ldots,\boldsymbol{A}_n\}$.
     
     • 此时， $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的任一解都是最小二乘解.
  2. 若 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 是不相容的，则 $\boldsymbol{b}\notin \mathscr{R}(\boldsymbol{A})$.
     
     • 此时，最小二乘解表示 $\mathscr{R}(\boldsymbol{A})$ 中与 $\boldsymbol{b}$ “距离最近”的点所对应的 $\boldsymbol{x}$.
     • 几何上看，应该满足 $\boldsymbol{b}-\boldsymbol{A} \boldsymbol{x}^{*} \perp \mathscr{R}(\boldsymbol{A})$.

---

最小二乘解的几何意义

$$\left\|\boldsymbol{A} \boldsymbol{x}^{*}-\boldsymbol{b}\right\|_{2}=\min _{\boldsymbol{x} \in \mathbb{C}^{n}}\|\boldsymbol{A} \boldsymbol{x}-\boldsymbol{b}\|_{2}$$

变换 $\boldsymbol{A}$ 的值空间 $\mathscr{R}(\boldsymbol{A})$ 中与 $\boldsymbol{b}$ 距离最近的点 $\boldsymbol{A}\boldsymbol{x}^*$ 对应的原向量 $\boldsymbol{x}^*$.

• 注 最小二乘解不一定具有唯一性！

---

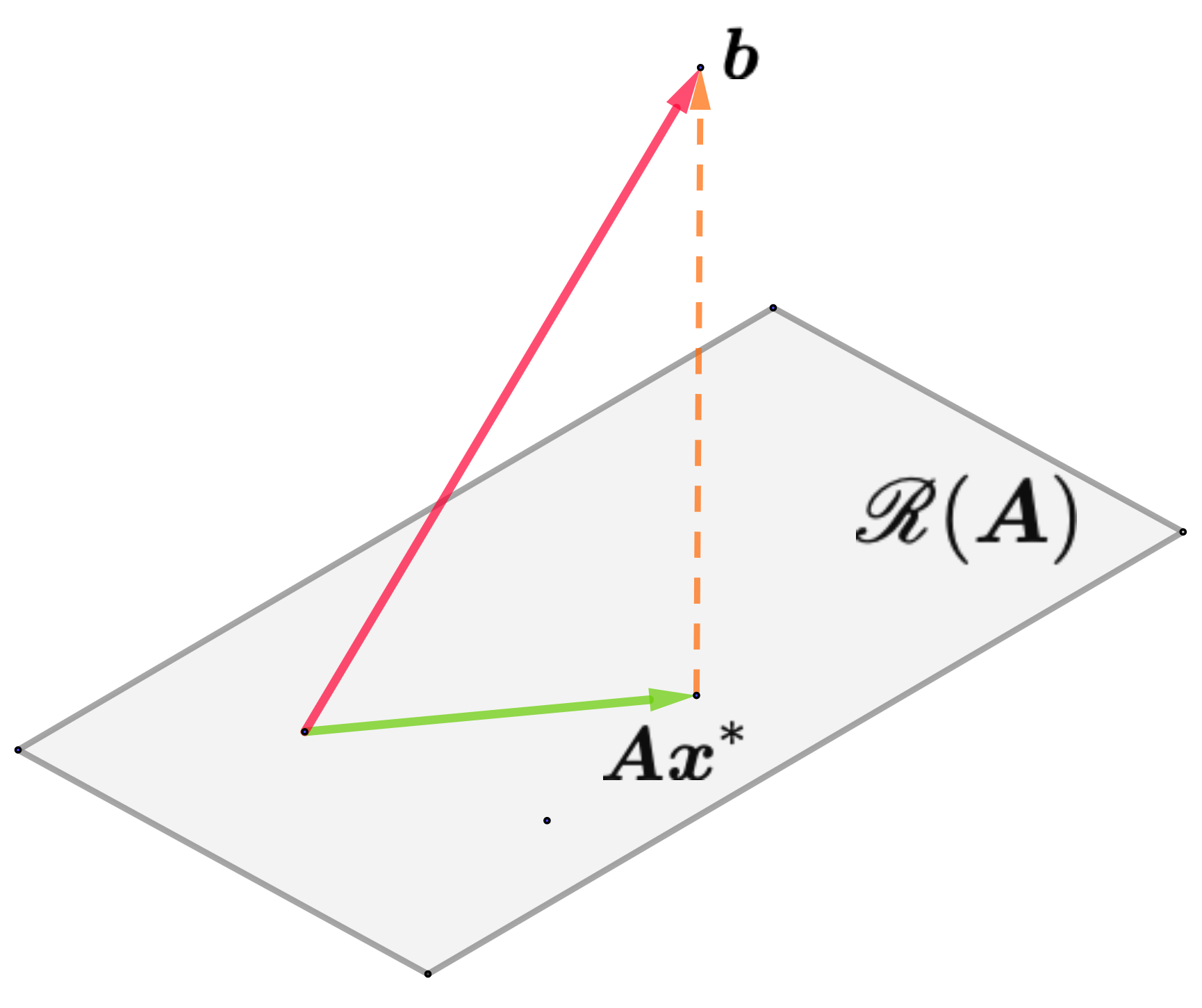
定理 设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$，$\boldsymbol{x}\in\mathbb{C}^n$，$\boldsymbol{b}\in\mathbb{C}^m$，则方程组 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的全部最小二乘解为

$$\boldsymbol{x}^*=\boldsymbol{A}^{+} \boldsymbol{b}+\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{t} \quad\left(\forall \boldsymbol{t} \in \mathbb{C}^{n}\right).$$

• 分析：对任意 $\boldsymbol{t} \in \mathbb{C}^{n}$,
  
  • $\boldsymbol{A} \boldsymbol{x}^{*}=\boldsymbol{A} \boldsymbol{A}^{+} \boldsymbol{b}+\boldsymbol{A}\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{t}$
    
    • $=\boldsymbol{A} \boldsymbol{A}^{+} \boldsymbol{b}+\left(\boldsymbol{A}-\boldsymbol{A} \boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{t}=\boldsymbol{A}\boldsymbol{A}^+\boldsymbol{b}$.

---

首先证明：$\boldsymbol{x}^*$ 是 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的最小二乘解.

• 对任意 $\boldsymbol{x} \in \mathbb{C}^{n}$，
  
  • $\langle \boldsymbol{b}-\boldsymbol{A} \boldsymbol{x}^{*}, \boldsymbol{A} \boldsymbol{x}\rangle=(\boldsymbol{A} \boldsymbol{x})^{\mathrm{H}} \boldsymbol{b}-(\boldsymbol{A} \boldsymbol{x})^{\mathrm{H}} \boldsymbol{A} \boldsymbol{x}^{*}$,
    
    • $=\boldsymbol{x}^{\mathrm{H}} \boldsymbol{A}^{\mathrm{H}} \boldsymbol{b}-\boldsymbol{x}^{\mathrm{H}} \boldsymbol{A}^{\mathrm{H}} \boldsymbol{A} \boldsymbol{A}^{+} \boldsymbol{b}=0$.
  • 由此可知 $\boldsymbol{A} \boldsymbol{x}^{*}-\boldsymbol{b} \perp \boldsymbol{A} \boldsymbol{x}$.
• 由勾股定理，
• $\|\boldsymbol{A} \boldsymbol{x}-\boldsymbol{b}\|_{2}^{2}=\left\|\boldsymbol{A} \boldsymbol{x}-\boldsymbol{b}+\boldsymbol{A} \boldsymbol{x}^{*}-\boldsymbol{A} \boldsymbol{x}^{*}\right\|_{2}^{2}$
  
  • $=\left\|\boldsymbol{A}\left(\boldsymbol{x}-\boldsymbol{x}^{*}\right)+\left(\boldsymbol{A} \boldsymbol{x}^{*}-\boldsymbol{b}\right)\right\|_{2}^{2}$
  • $=\left\|\boldsymbol{A}\left(\boldsymbol{x}-\boldsymbol{x}^{*}\right)\right\|_{2}^{2}+\left\|\left(\boldsymbol{A} \boldsymbol{x}^{*}-\boldsymbol{b}\right)\right\|_{2}^{2} \geq\left\|\left(\boldsymbol{A} \boldsymbol{x}^{*}-\boldsymbol{b}\right)\right\|_{2}^{2}$.
• 也即 $\boldsymbol{x}^*$ 是 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的最小二乘解.

---

进一步证明：若 $\boldsymbol{x}^*$ 是 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的最小二乘解，则存在 $\boldsymbol{t} \in \mathbb{C}^{n}$ ，使得 $\boldsymbol{x}^*=\boldsymbol{A}^{+} \boldsymbol{b}+\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{t}$.

• 因为 $\boldsymbol{A}^+\boldsymbol{b}$ 是 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的最小二乘解，故 $\|\boldsymbol{A} \boldsymbol{x}^*-\boldsymbol{b}\|_2=\left\|\boldsymbol{A}\boldsymbol{A}^{+} \boldsymbol{b}-\boldsymbol{b}\right\|_2$.
• $\|\boldsymbol{A} \boldsymbol{x}^*-\boldsymbol{b}\|_{2}^{2}=\left\|\boldsymbol{A}\left(\boldsymbol{x}^*-\boldsymbol{A}^{+} \boldsymbol{b}\right)+\left(\boldsymbol{A} \boldsymbol{A}^{+} \boldsymbol{b}-\boldsymbol{b}\right)\right\|_{2}^{2}$
  
  • $=\left\|\boldsymbol{A}\left(\boldsymbol{x}^*-\boldsymbol{A}^{+} \boldsymbol{b}\right)\right\|_{2}^{2}+\left\|\boldsymbol{A} \boldsymbol{A}^{+} \boldsymbol{b}-\boldsymbol{b}\right\|_{2}^{2}$.
• 从而可知 $\left\|\boldsymbol{A}\left(\boldsymbol{x}^*-\boldsymbol{A}^{+} \boldsymbol{b}\right)\right\|_{2}^{2}=0$，即 $\boldsymbol{A}\left(\boldsymbol{x}^*-\boldsymbol{A}^{+} \boldsymbol{b}\right)=\boldsymbol{0}$.
• 这说明 $\boldsymbol{x}^*-\boldsymbol{A}^+\boldsymbol{b}$ 是 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}$ 的解.
• 故存在 $\boldsymbol{t} \in \mathbb{C}^{n}$ ，使得 $\boldsymbol{x}^*-\boldsymbol{A}^{+} \boldsymbol{b}=\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{t}$.
• 即 ${\boldsymbol{x}}^*={\boldsymbol{A}}^{+} {\boldsymbol{b}}+\left({\boldsymbol{I}}-{\boldsymbol{A}}^{+} {\boldsymbol{A}}\right) {\boldsymbol{t}}$.

---

例 设

$$\boldsymbol{A}=\left[\begin{array}{rrrr}{1} & {1} & {2} & {4} \\ {-1} & {-1} & {-1} & {-2} \\ {3} & {3} & {2} & {4}\end{array}\right], \quad \boldsymbol{b}=\left[\begin{array}{l}{4} \\ {1} \\ {c}\end{array}\right], \quad \boldsymbol{x}=\left[\begin{array}{c}{x_{1}} \\ {x_{2}} \\ {x_{3}} \\ {x_{4}}\end{array}\right] \in \mathbb{C}^{4}$$

(1) 常数 $c$ 满足什么条件时， $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 是不相容的;

(2) 当 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 不相容时，求其最小二乘解.

---

提示

• $[\boldsymbol{A}\;\;\boldsymbol{b}]\to \left[\begin{array}{llllc}{1} & {1} & {2} & {4} & {4} \\ {0} & {0} & {1} & {2} & {5} \\ {0} & {0} & {0} & {0} & {c+8}\end{array}\right]$.
• 当 $c\ne-8$ 时，方程组 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 不相容.
• $\boldsymbol{A}$ 的满秩分解 $\boldsymbol{A}=\left[\begin{array}{rr}{1} & {2} \\ {-1} & {-1} \\ {3} & {2}\end{array}\right]\left[\begin{array}{cccc}{1} & {1} & {0} & {0} \\ {0} & {0} & {1} & {2}\end{array}\right]=\boldsymbol{F} \boldsymbol{G}$.
• $\boldsymbol{F}^{\mathrm{T}} \boldsymbol{F}=\left[\begin{array}{ccc}{1} & {-1} & {3} \\ {2} & {-1} & {2}\end{array}\right]\left[\begin{array}{cc}{1} & {2} \\ {-1} & {-1} \\ {3} & {2}\end{array}\right]=\left[\begin{array}{cc}{11} & {9} \\ {9} & {9}\end{array}\right]$.
• $\boldsymbol{F}^{+}=\left(\boldsymbol{F}^{\mathrm{T}} \boldsymbol{F}\right)^{-1} \boldsymbol{F}^{\mathrm{T}}=\frac{1}{18}\left[\begin{array}{ccc}{-9} & {0} & {9} \\ {13} & {-2} & {-5}\end{array}\right]$.

---

• $\boldsymbol{G} \boldsymbol{G}^{\mathrm{T}}=\left[\begin{array}{cccc}{1} & {1} & {0} & {0} \\ {0} & {0} & {1} & {2}\end{array}\right]\left[\begin{array}{cc}{1} & {0} \\ {1} & {0} \\ {0} & {1} \\ {0} & {2}\end{array}\right]=\left[\begin{array}{cc}{2} & {0} \\ {0} & {5}\end{array}\right]$.
• $\boldsymbol{G}^{+}=\boldsymbol{G}^{\mathrm{T}}\left(\boldsymbol{G} \boldsymbol{G}^{\mathrm{T}}\right)^{-1}=\frac{1}{10}\left[\begin{array}{ll}{5} & {0} \\ {5} & {0} \\ {0} & {2} \\ {0} & {4}\end{array}\right]$.
• 于是 $\boldsymbol{A}^{+}=\boldsymbol{G}^{+} \boldsymbol{F}^{+}=\frac{1}{180}\left[\begin{array}{ccc}{-45} & {0} & {45} \\ {-45} & {0} & {45} \\ {26} & {-4} & {-10} \\ {52} & {-8} & {-20}\end{array}\right]$.

---

• $\boldsymbol{A}^{+} \boldsymbol{b}=\frac{1}{180}\left[\begin{array}{ccc}{-45} & {0} & {45} \\ {-45} & {0} & {45} \\ {26} & {-4} & {-10} \\ {52} & {-8} & {-20}\end{array}\right]\left[\begin{array}{c}{4} \\ {1} \\ {c}\end{array}\right]=\frac{1}{36}\left[\begin{array}{c}{9 c-36} \\ {9 c-36} \\ {20-2 c} \\ {40-4 c}\end{array}\right].$
• $\boldsymbol{A}^{+} \boldsymbol{A}=\left[\begin{array}{cccc}{1 / 2} & {1 / 2} & {0} & {0} \\ {1 / 2} & {1 / 2} & {0} & {0} \\ {0} & {0} & {1 / 5} & {2 / 5} \\ {0} & {0} & {2 / 5} & {4 / 5}\end{array}\right]$.

---

• 综上，当 $c\ne8$ 时， $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的最小二乘解为
• $\boldsymbol{x}^{*}=\boldsymbol{A}^{+} \boldsymbol{b}+\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{t}$
  
  • $=\frac{1}{36}\left[\begin{array}{c}{9 c-36} \\ {9 c-36} \\ {20-2 c} \\ {40-4 c}\end{array}\right]+\left[\begin{array}{cccc}{1 / 2} & {-1 / 2} & {0} & {0} \\ {-1 / 2} & {1 / 2} & {0} & {0} \\ {0} & {0} & {4 / 5} & {-2 / 5} \\ {0} & {0} & {-2 / 5} & {1 / 5}\end{array}\right]\left[\begin{array}{c}{t_{1}} \\ {t_{2}} \\ {t_{3}} \\ {t_{4}}\end{array}\right]$
  • $=\frac{1}{36}\left[\begin{array}{c}{9 c-36} \\ {9 c-36} \\ {20-2 c} \\ {40-4 c}\end{array}\right]+\left[\begin{array}{c}{\left(t_{1}-t_{2}\right) / 2} \\ {-\left(t_{1}-t_{2}\right) / 2} \\ {2\left(2 t_{3}-t_{4}\right) / 5} \\ {-\left(2 t_{3}-t_{4}\right) / 5}\end{array}\right]$
  • $=\frac{1}{36}\left[\begin{array}{c}{9 c-36} \\ {9 c-36} \\ {20-2 c} \\ {40-4 c}\end{array}\right]+\left[\begin{array}{c}{k_{1}} \\ {-k_{1}} \\ {2 k_{2}} \\ {-k_{2}}\end{array}\right] \quad (k_{1}, k_{2} \in \mathbb{C})$.

---

极小范数最小二乘解

若 $\boldsymbol{x}^{* *} \in \mathbb{C}^{n}$ 是 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的最小二乘解，且满足

$$\left\|\boldsymbol{x}^{* *}\right\|_{2}=\min _{\boldsymbol{t} \in \mathbb{C}^{n}}\left\{\left\|\boldsymbol{x}^{*}\right\|_{2} \bigg| \boldsymbol{x}^{*}=\boldsymbol{A}^{+} \boldsymbol{b}+\left(\boldsymbol{I}_{n}-\boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{t}\right\}$$

则称 $\boldsymbol{x}^{* *}$ 是方程组 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的 极小范数最小二乘解 (Minimal Norm Least Square Solution)

• 定理 设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$，$\boldsymbol{x}\in\mathbb{C}^n$，$\boldsymbol{b}\in\mathbb{C}^m$，则方程组 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的极小范数最小二乘解为 $\boldsymbol{x}^{**}=\boldsymbol{A}^{+} \boldsymbol{b}.$

---

只需证明：对任意的最小二乘解 $\boldsymbol{x}^*$，总有 $\|\boldsymbol{x}^*\|\geq \|\boldsymbol{x}^{**}\|$.

• 先证对任意 $\boldsymbol{t} \in \mathbb{C}^{n}$ ，有 $\boldsymbol{A}^{+} \boldsymbol{b} \perp\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right)\boldsymbol{t}$.
• $\langle\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right)\boldsymbol{t}, \boldsymbol{A}^{+} \boldsymbol{b}\rangle=\boldsymbol{b}^{\mathrm{H}}\left(\boldsymbol{A}^{+}\right)^{\mathrm{H}}\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right)\boldsymbol{t}$
  
  • $=\boldsymbol{b}^{\mathrm{H}}\left[\left(\boldsymbol{A}^{+}\right)^{\mathrm{H}}-\left(\boldsymbol{A}^{+}\right)^{\mathrm{H}} \boldsymbol{A}^{+} \boldsymbol{A}\right] \boldsymbol{t}$
  • $=\boldsymbol{b}^{\mathrm{H}}\left[\left(\boldsymbol{A}^{+}\right)^{\mathrm{H}}-\left(\boldsymbol{A}^{+}\right)^{\mathrm{H}}\left(\boldsymbol{A}^{+} \boldsymbol{A}\right)^{\mathrm{H}}\right] \boldsymbol{t}$
  • $=\boldsymbol{b}^{\mathrm{H}}\left[\left(\boldsymbol{A}^{+}\right)^{\mathrm{H}}-\left(\boldsymbol{A}^{+} \boldsymbol{A} \boldsymbol{A}^{+}\right)^{\mathrm{H}}\right] \boldsymbol{t}=0$.
• 再由勾股定理,
  
  • $\left\|\boldsymbol{x}^{*}\right\|_{2}^{2}=\left\|\boldsymbol{A}^{+} \boldsymbol{b}+\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{t}\right\|_{2}^{2}$
    
    • $=\left\|\boldsymbol{A}^{+} \boldsymbol{b}\right\|_{2}^{2}+\left\|\left(\boldsymbol{I}-\boldsymbol{A}^{+} \boldsymbol{A}\right) \boldsymbol{t}\right\|_{2}^{2} \geq\left\|\boldsymbol{A}^{+} \boldsymbol{b}\right\|_{2}^{2}$.

---

例

$$\boldsymbol{A}=\left[\begin{array}{llll}{1} & {2} & {0} & {1} \\ {0} & {1} & {1} & {3} \\ {2} & {5} & {1} & {5}\end{array}\right], \boldsymbol{b}=\left[\begin{array}{l}{3} \\ {2} \\ {3}\end{array}\right], \boldsymbol{x}=\left[\begin{array}{c}{x_{1}} \\ {x_{2}} \\ {x_{3}} \\ {x_{4}}\end{array}\right] \in \mathbb{C}^{4}$$

(1) 判断 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 是否相容;

(2) 若不相容，求 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 的极小范数最小二乘解.

---

提示：

• $[\boldsymbol{A}\;\;\boldsymbol{b}]\to\left[\begin{array}{lllc}{1} & {2} & {0} & 1& 3 \\ {0} & {1} & {1} & 3& 2 \\ {0} & {0} & {0} & {0} & {-5}\end{array}\right]$，故 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 不相容.
• $\boldsymbol{A}$ 的满秩分解 $\boldsymbol{A}=\left[\begin{array}{ll}{1} & {2} \\ {0} & {1} \\ {2} & {5}\end{array}\right]\left[\begin{array}{llll}{1} & {0} & {-2} & {-5} \\ {0} & {1} & {1} & {3}\end{array}\right]=\boldsymbol{F} \boldsymbol{G}$.
• $\boldsymbol{F}^{\mathrm{T}} \boldsymbol{F}=\left[\begin{array}{lll}{1} & {0} & {2} \\ {2} & {1} & {5}\end{array}\right]\left[\begin{array}{ll}{1} & {2} \\ {0} & {1} \\ {2} & {5}\end{array}\right]=\left[\begin{array}{ll}{5} & {12} \\ {12} & {30}\end{array}\right]$.
• $\boldsymbol{F}^{+}=\left(\boldsymbol{F}^{\mathrm{T}} \boldsymbol{F}\right)^{-1} \boldsymbol{F}^{\mathrm{T}}=\frac{1}{6}\left[\begin{array}{rrr}{6} & {-12} & {0} \\ {-2} & {5} & {1}\end{array}\right]$.

---

• $\boldsymbol{G} \boldsymbol{G}^{\mathrm{T}}=\left[\begin{array}{rrrr}{1} & {0} & {-2} & {-5} \\ {0} & {1} & {1} & {3}\end{array}\right]\left[\begin{array}{rr}{1} & {0} \\ {0} & {1} \\ {-2} & {1} \\ {-5} & {3}\end{array}\right]=\left[\begin{array}{cc}{30} & {-17} \\ {-17} & {11}\end{array}\right]$.
• $\boldsymbol{G}^{+}=\boldsymbol{G}^{\mathrm{T}}\left(\boldsymbol{G} \boldsymbol{G}^{\mathrm{T}}\right)^{-1}=\frac{1}{41}\left[\begin{array}{rr}{11} & {17} \\ {17} & {30} \\ {-5} & {-4} \\ {-4} & {5}\end{array}\right]$.
• 于是 $\boldsymbol{A}^{+}=\boldsymbol{G}^{+} \boldsymbol{F}^{+}=\frac{1}{246}\left[\begin{array}{rrr}{32} & {-47} & {17} \\ {42} & {-54} & {30} \\ {-22} & {40} & {-4} \\ {-34} & {73} & {5}\end{array}\right]$.
• 故 $\boldsymbol{x}^{* *}=\boldsymbol{A}^{+} \boldsymbol{b}=\frac{1}{246}\left[\begin{array}{rrr}{32} & {-47} & {17} \\ {42} & {-54} & {30} \\ {-22} & {40} & {-4} \\ {-34} & {73} & {5}\end{array}\right]\left[\begin{array}{l}{3} \\ {2} \\ {3}\end{array}\right]=\frac{1}{246}\left[\begin{array}{c}{53} \\ {108} \\ {2} \\ {59}\end{array}\right]$.

---

矩阵的条件数（Condition Number）

$$\kappa(\boldsymbol{A})=\|\boldsymbol{A}\|\left\|\boldsymbol{A}^+\right\|$$

• 其中 $\|\cdot\|$ 为矩阵的某个诱导范数.
• 条件数一般用来度量输入的微小误差对输出结果可能产生的影响程度.
• 条件数偏大，意味着求解 $\boldsymbol{A}$ 相关的最小二乘解时，可能存在某种病态（ill-conditioned）的情况,
  
  • 即：$\boldsymbol{A}$ 中的微小误差可能会导致最小二乘解解的较大偏差.

---

小结

• M-P 逆的定义与性质
  
  • 与可逆矩阵逆的关系
  • 与左逆、右逆的联系
  • 计算公式
• M-P 逆的应用
  
  • 最小二乘解
  • 极小范数最小二乘解

---

A Brief History of M-P Inverse[1]

• was independently described by
  
  • E. H. Moore in 1920
  • Arne Bjerhammar in 1951
  • Roger Penrose in 1955
• Erik Ivar Fredholm introduced the concept of a pseudoinverse(伪逆) of integral operators in 1903.

---

Roger Penrose (1931-)[2]

• English mathematical physicist, mathematician and philosopher of science
• Emeritus Rouse Ball Professor of Mathematics at the University of Oxford and an emeritus fellow of Wadham College, Oxford
• contributions to
  
  • the mathematical physics of general relativity and cosmology
  • shared with Stephen Hawking for the Penrose–Hawking singularity theorems

---

• 1955, A Generalized Inverse for Matrices." Proc. Cambridge Phil. Soc. 51, 406-413, 1955
  
  • 重新发明了矩阵的广义逆
• 1958, Tensor methods in algebraic geometry, for Ph.D in Cambridge
  
  • 代数几何学中的张量方法
• 1965, with Hawking, Gravitational collapse and space-time singularities
  
  • 证明了 奇点（例如黑洞）可以从毁坏中的巨星体的重力坍缩现象中形成
• 1967, invented the twistor theory
• 1974, discover Penrose tilings
• 1979, formulated strong censorship hypothesis
  
  • 审查猜想是广义相对论中最重要的未决问题之一

---

娱乐数学家与具争议性的哲学家[3]

• Roger Penrose, The Emperor's New Mind: Concerning Computers, Minds and The Laws of Physics, 1989
  
  • known laws of physics are inadequate to explain the phenomenon of consciousness
  • 认为作为一种算法确定性的系统，当前的电子计算机无法产生智能
  • 反对认为大脑的推理过程是完全的图灵可计算的观点
    
    • 若此则大脑可被足够复杂的电子计算机复制
  • 声称意识是超越数理逻辑的，因为诸如停机问题的不可解性质和哥德尔不完备定理导致基于算法的逻辑系统不能产生具有人类智能特性的智能（比如，对数学的洞见）
• 受到了来自数学家、计算机科学家和哲学家的广泛批评
  
  • Marvin Minsky：“在科学探索的道路上，仅靠攻击现有的科学知识将无法获取新的原理。但在我看来，这就是彭罗斯的探索手段”

---

Penrose Tilings