1.2 线性变换及其矩阵表示

高等工程数学 讲义 2024AU

---

---

1.2.1 线性变换的定义

设 $V_1,V_2$ 同为数域 $F$ 上的线性空间， $T$ 是 $V_1$ 到 $V_2$ 的映射，若对 $\forall\boldsymbol{\alpha},\boldsymbol{\beta}\in V_1$ 和 $\forall k\in F$

• $T(\boldsymbol{\alpha}+\boldsymbol{\beta})=T\boldsymbol{\alpha}+T\boldsymbol{\beta}$
• $T(k\boldsymbol{\alpha})=kT\boldsymbol{\alpha}$

则称 $T$ 为线性空间 $V_1$ 到 $V_2$ 的 线性变换（或 线性算子，Linear Transformation/Map/Operator）

---

线性变换的性质

设 $T$ 是 $V_1$ 到 $V_2$ 的线性变换，则

• $T\boldsymbol{0}=\boldsymbol{0}$
• 设 $\boldsymbol{B}=\{\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,...,\boldsymbol{\alpha}_n\}$ 为 $V_1$ 中的一组向量，记 $T\boldsymbol{B}=[T\boldsymbol{\alpha}_1\;T\boldsymbol{\alpha}_2...T\boldsymbol{\alpha}_n]$
  
  • 对任意的 $\boldsymbol{x}\in F^n$， $T\left(\boldsymbol{Bx}\right)=\left(T\boldsymbol{B}\right)\boldsymbol{x}$
  • 对任意的 $\boldsymbol{A}\in F^{n\times m}$，$T\left(\boldsymbol{BA}\right)=\left(T\boldsymbol{B}\right)\boldsymbol{A}$

---

线性变换与线性相关性

设 $T$ 是 $V_1\to V_2$ 的线性变换

• $\boldsymbol{\alpha}_1,...,\boldsymbol{\alpha}_n\in V_1$ 线性相关，则 $T\boldsymbol{\alpha}_1,...,T\boldsymbol{\alpha}_n$ 必线性相关
• 若 $T\boldsymbol{\alpha}_1,...,T\boldsymbol{\alpha}_n$ 线性无关，则 $\boldsymbol{\alpha}_1,...,\boldsymbol{\alpha}_n$ 线性无关
• 思考 $\boldsymbol{\alpha}_1,...,\boldsymbol{\alpha}_n\in V_1$ 线性无关， $T\boldsymbol{\alpha}_1,...,T\boldsymbol{\alpha}_n$ 是否必线性无关？
  
  • 若 $T\boldsymbol{\alpha}_1,...,T\boldsymbol{\alpha}_n$ 线性相关，则 $\boldsymbol{\alpha}_1,...,\boldsymbol{\alpha}_n$ 一定线性相关吗？

---

例 以下哪些变换是线性变换（设 $x_1,x_2\in\mathbb{R}$）

1. $T_1\begin{bmatrix}x_1 \\ x_2\end{bmatrix}=x_1$
2. $T_2\begin{bmatrix}x_1 \\ x_2\end{bmatrix}=\begin{bmatrix}x_2 \\ x_1\end{bmatrix}$
3. $T_3\begin{bmatrix}x_1 \\ x_2\end{bmatrix}=\begin{bmatrix}x_1+x_2 \\ x_2-x_1\end{bmatrix}$
4. $T_4\begin{bmatrix}x_1 \\ x_2\end{bmatrix}=\begin{bmatrix}x_1+1 \\ x_2\end{bmatrix}$

答：除了 4 不是，其余都是.

思考：以上变换有什么样的几何意义？

---

例 在线性空间 $P_n(t)$ 上定义

$$T p(t)=\frac{\mathrm{d}}{\mathrm{d} t} p(t), \quad \forall p(t) \in {P}_{n}(t)$$

则 $T$ 是 $P_n(t)$ 到 $P_{n-1}(t)$ 的线性算子.

• $P_n(t)$ 表示次数不超过 $n$ 的实系数多项式全体.

---

例 设 $\boldsymbol{A} \in \mathbb{C}^{m \times n}$ ， $\forall \boldsymbol{x} \in \mathbb{C}^{n}$ ，定义映射 $T$ 为

$$T\boldsymbol{x}=\boldsymbol{A}\boldsymbol{x}$$

则 $T$ 是 $\mathbb{C}^{n}$ 到 $\mathbb{C}^{m}$ 的线性变换。

• 一个矩阵就定义了(对应于)一个线性变换

---

线性变换的判定

例 设 $\boldsymbol{B}=\left\{\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}\right\}$ 是线性空间 $V$ 的一个基，定义映射 $T$ 为： $\forall x_{1}, x_{2}, x_{3} \in \mathbb{R}$

$$\begin{aligned} &T\left(x_{1} \boldsymbol{\alpha}_{1}+x_{2} \boldsymbol{\alpha}_{2}+x_{3} \boldsymbol{\alpha}_{3}\right)\\ &\quad =\left(x_{1}+x_{2}+x_{3}\right) \boldsymbol{\alpha}_{1}+\left(x_{2}+x_{3}\right) \boldsymbol{\alpha}_{2}+x_{3} \boldsymbol{\alpha}_{3} \end{aligned}$$

（1）证明： $T$ 是 $V\to V$ 的线性变換;

（2）设 $\boldsymbol{\beta}_{0}=\boldsymbol{\alpha}_{1}+2 \boldsymbol{\alpha}_{2}+3 \boldsymbol{\alpha}_{3}$ , 试求 $T\boldsymbol{\beta}_0$.

---

提示：(1) 证明 $T$ 是线性变换

• 任取 $\boldsymbol{\alpha},\boldsymbol{\beta}\in V$，记 $\boldsymbol{\alpha}=\boldsymbol{\boldsymbol{B}x}$，$\boldsymbol{\beta}=\boldsymbol{\boldsymbol{B}y}$，其中 $\boldsymbol{x},\boldsymbol{y}\in\mathbb{R}^3$.
• 由已知，$T \left(\boldsymbol{B}\left[\begin{array}{l}{x_{1}} \\ {x_{2}} \\ {x_{3}}\end{array}\right]\right)={\boldsymbol{B}}\left[\begin{array}{ccc}{1} & {1} & {1} \\ {0} & {1} & {1} \\ {0} & {0} & {1}\end{array}\right]\left[\begin{array}{l}{x_{1}} \\ {x_{2}} \\ {x_{3}}\end{array}\right]$
  
  • 记为 $T\left(\boldsymbol{B}\boldsymbol{x}\right)={\boldsymbol{B}} \boldsymbol{A} \boldsymbol{x}$.
• $T(\boldsymbol{\alpha}+\boldsymbol{\beta})=T({\boldsymbol{B}} \boldsymbol{x}+{\boldsymbol{B}} \boldsymbol{y})=T({\boldsymbol{B}}(\boldsymbol{x}+\boldsymbol{y}))$
  
  • $={\boldsymbol{B}} \boldsymbol{A}(\boldsymbol{x}+\boldsymbol{y})={\boldsymbol{B}}\boldsymbol{A}\boldsymbol{x}+{\boldsymbol{B}}\boldsymbol{A}\boldsymbol{y}=T\boldsymbol{\alpha}+T\boldsymbol{\beta}$.
• $T(k \boldsymbol{\alpha})=T(k{\boldsymbol{B}}\boldsymbol{x})=T({\boldsymbol{B}} k \boldsymbol{x})={\boldsymbol{B}} \boldsymbol{A}(k \boldsymbol{x})=k {\boldsymbol{B}} \boldsymbol{A} \boldsymbol{x}=k T\boldsymbol{\alpha}$.

---

(2) 求 $T\boldsymbol{\beta}_0$

• $T \boldsymbol{\beta}_{0}=T\left(\boldsymbol{\alpha}_{1}+2 \boldsymbol{\alpha}_{2}+3 \boldsymbol{\alpha}_{3}\right)$
  
  • $=(1+2+3) \boldsymbol{\alpha}_{1}+(2+3) \boldsymbol{\alpha}_{2}+3 \boldsymbol{\alpha}_{3}$
  • $=6 \boldsymbol{\alpha}_{1}+5 \boldsymbol{\alpha}_{2}+3 \boldsymbol{\alpha}_{3}$
• 或 $T \boldsymbol{\beta}_{0}=\boldsymbol{B} \left[\begin{array}{ccc}{1} & {1} & {1} \\ {0} & {1} & {1} \\ {0} & {0} & {1}\end{array}\right]\left[\begin{array}{l}{1} \\ {2} \\ {3}\end{array}\right]=6 \boldsymbol{\alpha}_{1}+5 \boldsymbol{\alpha}_{2}+3 \boldsymbol{\alpha}_{3}$

---

1.2.2 线性变换的矩阵表示

设 $T$ 是 $V^n\to V^m$ 的线性变换， $\boldsymbol{B}_{\boldsymbol{\alpha}}=\left\{\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{n}\right\}$ 与 $\boldsymbol{B}_{\boldsymbol{\beta}}=\left\{\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2}, \cdots, \boldsymbol{\beta}_{m}\right\}$ 分别是 $V^n$ 与 $V^m$ 的基.

• 设 ${T} \boldsymbol{\alpha}_{i}=\boldsymbol{B}_{\boldsymbol{\beta}} \boldsymbol{A}_{i},\;i=1,2,\ldots,n$,
  
  • $\boldsymbol{A}_i$ 为 $T\boldsymbol{\alpha}_i$ 在基 $\boldsymbol{B}_{\boldsymbol{\beta}}$ 下的坐标.
• 记 $\boldsymbol{A}=[\boldsymbol{A}_1\;\boldsymbol{A}_2\;\ldots\;\boldsymbol{A}_n]$,
• 则 ${T} \boldsymbol{B}_{\boldsymbol{\alpha}}=\left\{{T} \boldsymbol{\alpha}_{1}, {T} \boldsymbol{\alpha}_{2}, \ldots, {T} \boldsymbol{\alpha}_{n}\right\}=\boldsymbol{B}_{\boldsymbol{\beta}}\{\boldsymbol{A}_1,\boldsymbol{A}_2,\ldots,\boldsymbol{A}_n\}=\boldsymbol{B}_{\boldsymbol{\beta}}\boldsymbol{A}$.
• 称 $\boldsymbol{A}$ 为线性变换 $T$ 在 基偶 $\{\boldsymbol{B}_{\boldsymbol{\alpha}},\boldsymbol{B}_{\boldsymbol{\beta}}\}$ 下的矩阵.

---

特别地，

若 $T$ 是 $V^n\to V^n$ 的线性变换，且取

$$\boldsymbol{B}_{\boldsymbol{\beta}}=\boldsymbol{B}_{\boldsymbol{\alpha}}$$

• 则 $\boldsymbol{A}$ 是 $n$ 阶方阵，称为 $T$ 在基 $\boldsymbol{B}_{\boldsymbol{\alpha}}$ 下的 矩阵.

---

求线性变换对应的矩阵

例 定义 $\mathbb{R}^3$ 上的线性算子

$$T \boldsymbol{x}=\left[\begin{array}{l}{5 x_{1}+4 x_{2}+2 x_{3}} \\ {4 x_{1}+5 x_{2}+2 x_{3}} \\ {2 x_{1}+2 x_{2}+2 x_{3}}\end{array}\right], \quad \boldsymbol{x}=\left[\begin{array}{c} x_1\\ x_2\\ x_3\end{array}\right]\in \mathbb{R}^{3}$$

求 $T$ 在基 $\boldsymbol{B}=\left\{\left[\begin{array}{l}{2} \\ {2} \\ {1}\end{array}\right],\left[\begin{array}{r}{-1} \\ {1} \\ {0}\end{array}\right],\left[\begin{array}{r}{-1} \\ {0} \\ {2}\end{array}\right]\right\}$ 下的矩阵.

---

提示

• 记 $\boldsymbol{A}=\begin{bmatrix} 5 & 4 & 2 \\ 4 & 5 & 2 \\ 2 & 2 & 2 \end{bmatrix}$，则 $T\boldsymbol{x}=\boldsymbol{Ax}$.
• 记 $\boldsymbol{B}=\{\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\boldsymbol{\beta}_3\}$，于是
• $T\boldsymbol{\beta}_1=\boldsymbol{A\beta}_1=\boldsymbol{A}\begin{bmatrix} 2 \\ 2 \\ 1 \end{bmatrix}=\begin{bmatrix} 20 \\ 20 \\ 10 \end{bmatrix}=\begin{bmatrix} 2 & -1 & -1 \\ 2 & 1 & 0 \\ 1 & 0 & 2 \end{bmatrix}\begin{bmatrix} 10 \\ 0 \\ 0 \end{bmatrix}=\boldsymbol{B}\left[\begin{array}{c} 10 \\ 0 \\ 0\end{array}\right]$

---

• 同理可得
  
  • $T\boldsymbol{\beta}_2=\boldsymbol{B}\left[\begin{array}{c} 0 \\ 1 \\ 0\end{array}\right]$,
  • $T\boldsymbol{\beta}_3=\boldsymbol{B}\left[\begin{array}{c} 0 \\ 0 \\ 1\end{array}\right]$.
• 故 $T$ 在基 $\boldsymbol{B}$ 下的矩阵为 $\boldsymbol{A}=\left[\begin{array}{ccc}{10} & {} \\ {} & {1} \\ {} & {} & {1}\end{array}\right]$.

---

例 设 $\boldsymbol{B}_{\boldsymbol{\alpha}}=\left\{\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}\right\}$ 和 $\boldsymbol{B}_{\boldsymbol{\beta}}=\left\{\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2}, \boldsymbol{\beta}_{3}\right\}$ 都是线性空间 $V^3$ 的基，从 $\boldsymbol{B}_{\boldsymbol{\alpha}}$ 到 $\boldsymbol{B}_{\boldsymbol{\beta}}$ 的过渡矩阵为

$$\boldsymbol{P}=\left[\begin{array}{rrr}{1} & {0} & {1} \\ {0} & {-1} & {0} \\ {-1} & {0} & {1}\end{array}\right]$$

设 $V^3$ 上的线性变换 $T$ 满足

$$\begin{array}{l} T\left(\boldsymbol{\alpha}_{1}+2 \boldsymbol{\alpha}_{2}+3 \boldsymbol{\alpha}_{3}\right)=\boldsymbol{\beta}_{1}+\boldsymbol{\beta}_{2}\\ T\left(2 \boldsymbol{\alpha}_{1}+\boldsymbol{\alpha}_{2}+2 \boldsymbol{\alpha}_{3}\right)=\boldsymbol{\beta}_{2}+\boldsymbol{\beta}_{3} \\ {T\left(\boldsymbol{\alpha}_{1}+3 \boldsymbol{\alpha}_{2}+4 \boldsymbol{\alpha}_{3}\right)=\boldsymbol{\beta}_{1}+\boldsymbol{\beta}_{3}} \end{array}$$

(1) 求 $T$ 在 $\boldsymbol{B}_{\boldsymbol{\beta}}$ 下的矩阵; (2) 求 $T\boldsymbol{\beta}_1$ 在基 $\boldsymbol{B}_{\boldsymbol{\alpha}}$ 下的坐标.

---

提示 （1）求 $T$ 在 $\boldsymbol{B}_{\boldsymbol{\beta}}$ 下的矩阵

• 由已知 $T\boldsymbol{B}_{\boldsymbol{\alpha}}\left[\begin{array}{ccc}{1} & {2} & {1} \\ {2} & {1} & {3} \\ {3} & {2} & {4}\end{array}\right]=\boldsymbol{B}_{\boldsymbol{\beta}}\left[\begin{array}{ccc}{1} & {0} & {1} \\ {1} & {1} & {0} \\ {0} & {1} & {1}\end{array}\right]$
• ${T} \boldsymbol{B}_{\boldsymbol{\beta}}={T} \boldsymbol{B}_{\boldsymbol{\alpha}} \boldsymbol{P}=\boldsymbol{B}_{\boldsymbol{\beta}}\left[\begin{array}{lll}{1} & {0} & {1} \\ {1} & {1} & {0} \\ {0} & {1} & {1}\end{array}\right]\left[\begin{array}{lll}{1} & {2} & {1} \\ {2} & {1} & {3} \\ {3} & {2} & {4}\end{array}\right]^{-1} \boldsymbol{P}=\boldsymbol{B}_{\boldsymbol{\beta}}\boldsymbol{A}$
• $\boldsymbol{A}=\left[\begin{array}{rrr}{-3} & {2} & {1} \\ {-5} & {5} & {3} \\ {6} & {-5} & {-2}\end{array}\right]$

---

（2）求 $T\boldsymbol{\beta}_1$ 在基 $\boldsymbol{B}_{\boldsymbol{\alpha}}$ 下的坐标

• 先求 $T\boldsymbol{\beta}_1$ 在基 $\boldsymbol{B}_{\boldsymbol{\beta}}$ 下的坐标
  
  • $\boldsymbol{y}=\boldsymbol{A}\left[\begin{array}{l}{1} \\ {0} \\ {0}\end{array}\right]=\left[\begin{array}{r}{-3} \\ {-5} \\ {6}\end{array}\right]$
• 故 $T\boldsymbol{\beta}_1$ 在基 $\boldsymbol{B}_{\boldsymbol{\alpha}}$ 下的坐标
  
  • $\boldsymbol{x}=P \boldsymbol{y}=\left[\begin{array}{lll}{3} & {5} & {9}\end{array}\right]^{\mathrm{T}}$

---

1.2.3 零空间与值空间

设 $T$ 是 $V^n\to V^m$ 的线性变换

• $T$ 的 零空间（核、核空间）
  
  • $\mathscr{N}({T})=\left\{\boldsymbol{\xi} \;|\; {T}\boldsymbol{\xi}=\boldsymbol{0},\boldsymbol{\xi} \in V^{n}\right\}$
  • $\mathrm{null}(T)=\mathrm{dim}(\mathscr{N}(T))$ 称为 $T$ 的 零度（Nullity）
• $T$ 的 值空间（值域、列空间）
  
  • $\mathscr{R}({T})=\left\{{\boldsymbol{\beta}} \;|\; {\boldsymbol{\beta}}={T}{\boldsymbol{\alpha}}, {\boldsymbol{\alpha}} \in V^{n}\right\}$
  • $\mathrm{rank}(T)=\mathrm{dim}(\mathscr{R}(T))$ 称为 $T$ 的 秩（Rank）

---

零度与秩的关系

定理 设 $T$ 是 $V^n\to V^m$ 的线性变换，则

$$\mathrm{rank}(T)+\mathrm{null}(T)=n.$$

---

证明：

• 设 $\mathrm{null}(T)=r$，取 $\{\boldsymbol{\alpha}_1,...,\boldsymbol{\alpha}_r\}$ 为 $\mathscr{N}(T)$ 的一组基.
• 将 $\{\boldsymbol{\alpha}_1,...,\boldsymbol{\alpha}_r\}$ 扩充为 $V^n$ 的基 $\{\boldsymbol{\alpha}_1,...,\boldsymbol{\alpha}_r,\boldsymbol{\alpha}_{r+1},...,\boldsymbol{\alpha}_n\}$.
• 接下来只需证明 $\{T\boldsymbol{\alpha}_{r+1},\ldots,T\boldsymbol{\alpha}_n\}$ 是 $\mathscr{R}(T)$ 的基，则 $\mathrm{rank}(T)=n-r$.

---

• 先证 $\mathscr{R}(T)$ 中的向量均可由 $\{T\boldsymbol{\alpha}_{r+1},\ldots,T\boldsymbol{\alpha}_n\}$ 线性表示.
  
  • 由值空间的定义，对 $\forall \boldsymbol{\eta}\in\mathscr{R}(T)$，$\exists\boldsymbol{\xi}\in V^n$，使得 $\boldsymbol{\eta}=T\boldsymbol{\xi}$.
  • 设 $\boldsymbol{\xi}=\sum\limits_{k=1}^nx_k\boldsymbol{\alpha}_k$.
  • 注意到对 $k=1,2,\ldots,r$，总有 $T\boldsymbol{\alpha}_k=\boldsymbol{0}$，于是
  • $\boldsymbol{\eta}=T\boldsymbol{\xi}=T\sum\limits_{k=1}^nx_k\boldsymbol{\alpha}_k=\sum\limits_{k=1}^nx_kT\boldsymbol{\alpha}_k=\sum\limits_{k=r+1}^nx_kT\boldsymbol{\alpha}_k$，即证.

---

• 再证 $\{T\boldsymbol{\alpha}_{r+1},T\boldsymbol{\alpha}_{r+2},...,T\boldsymbol{\alpha}_n\}$ 线性无关.
  
  • 设 $\sum\limits_{k=r+1}^nx_kT\boldsymbol{\alpha}_k=\boldsymbol{0}$，以下证明所有的 $x_k=0,\;k=r+1,...,n.$
  • 前式也即 $T\left(\sum\limits_{k=r+1}^nx_k\boldsymbol{\alpha}_k\right)=\boldsymbol{0}$，故 $\sum\limits_{k=r+1}^nx_k\boldsymbol{\alpha}_k\in\mathscr{N}(T)$.
  • $\{\boldsymbol{\alpha}_1,...,\boldsymbol{\alpha}_r\}$ 为 $\mathscr{N}(T)$ 的基，故 $\exists x_k,\;k=1,\ldots,r$，使得 $\sum\limits_{k=1}^rx_k\boldsymbol{\alpha}_k=\sum\limits_{k=r+1}^nx_k\boldsymbol{\alpha}_k$.
  • 也即 $\sum\limits_{k=1}^rx_k\boldsymbol{\alpha}_k-\sum\limits_{k=r+1}^nx_k\boldsymbol{\alpha}_k=\boldsymbol{0}$
  • 注意到 $\{\boldsymbol{\alpha}_1,...,\boldsymbol{\alpha}_n\}$ 线性无关，故必有 $x_k=0,\;k=1,2,\ldots,n$.

---

定理 设 $T$ 是 $V^n\to V^m$ 的线性变换，

$$\boldsymbol{B}_{\boldsymbol{\alpha}}=\left\{\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{n}\right\}, \boldsymbol{B}_{\boldsymbol{\beta}}=\left\{\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2}, \cdots, \boldsymbol{\beta}_{m}\right\}$$

分别是 $V^n$ 与 $V^m$ 的基， $T$ 在基偶 $\{\boldsymbol{B}_{\boldsymbol{\alpha}},\boldsymbol{B}_{\boldsymbol{\beta}}\}$ 下的矩阵为 $\boldsymbol{A}$ ，则

1. $\mathrm{rank}(T)=\mathrm{rank}(\boldsymbol{A})$
2. $\mathrm{null}(T)=n-\mathrm{rank}(\boldsymbol{A})$

3. $\mathrm{rank}(T)+\mathrm{null}(T)=n$

   • 推论 同一个线性变换在不同基偶下对应的矩阵具有相同的秩.

---

提示： $\mathrm{null}(T)=n-\mathrm{rank}(\boldsymbol{A})$.

• $\mathscr{N}(T)=\left\{\boldsymbol{\alpha}\big|T\boldsymbol{\alpha}=\boldsymbol{0}\right\}=\left\{\boldsymbol{B}_{\alpha}\boldsymbol{x}\big|T\boldsymbol{B}_{\alpha}\boldsymbol{x}=\boldsymbol{0},\boldsymbol{x}\in F^n\right\}$
  
  • $=\left\{\boldsymbol{B}_{\alpha}\boldsymbol{x}\big|\boldsymbol{B}_{\beta}\boldsymbol{Ax}=\boldsymbol{0},\boldsymbol{x}\in F^n\right\}$
  • $=\left\{\boldsymbol{B}_{\alpha}\boldsymbol{x}\big|\boldsymbol{Ax}=\boldsymbol{0},\boldsymbol{x}\in F^n\right\}=\left\{\boldsymbol{B}_{\alpha}\boldsymbol{x}\big|\boldsymbol{x}\in\mathscr{N}(\boldsymbol{A})\right\}$.
• 因为 $\boldsymbol{B}_{\alpha}$ 中的向量线性无关，故 $\mathscr{N}(\boldsymbol{A})$ 与 $\mathscr{N}(T)$ 是一一对应的.
• 进而可以验证 $\mathscr{N}(\boldsymbol{A})$ 与 $\mathscr{N}(T)$ 是同构的.
• 设 $\left\{\boldsymbol{x}_1,...,\boldsymbol{x}_{n-r}\right\}$ 是 $\mathscr{N}(\boldsymbol{A})$ 的基，可以证明 $\left\{\boldsymbol{B}_{\alpha}\boldsymbol{x}_1,...,\boldsymbol{B}_{\alpha}\boldsymbol{x}_{n-r}\right\}$ 也是 $\mathscr{N}(T)$ 的基. (自行练习)

---

提示： $\mathrm{rank}(T)=\mathrm{rank}(\boldsymbol{A})$.

• $\mathscr{R}(T)=\left\{\boldsymbol{\beta}=T\boldsymbol{\alpha}\big|\boldsymbol{\alpha}\in V^n\right\}=\left\{\boldsymbol{B}_{\beta}\boldsymbol{y}=T\boldsymbol{B}_{\alpha}\boldsymbol{x}\big|\boldsymbol{x}\in F^n\right\}$
  
  • $=\left\{\boldsymbol{B}_{\beta}\boldsymbol{y}=\boldsymbol{B}_{\beta}\boldsymbol{Ax}\big|\boldsymbol{x}\in F^n\right\}=\left\{\boldsymbol{B}_{\beta}\boldsymbol{y}\big|\boldsymbol{y}=\boldsymbol{Ax},\boldsymbol{x}\in F^n\right\}$
  • $=\left\{\boldsymbol{B}_{\beta}\boldsymbol{y}\big|\boldsymbol{y}\in\mathscr{R}(\boldsymbol{A})\right\}$
• 由此容易验证 $\mathscr{R}(\boldsymbol{A})$ 与 $\mathscr{R}(T)$ 同构.
• 设 $\left\{\boldsymbol{y}_1,...,\boldsymbol{y}_{r}\right\}$ 是 $\mathscr{R}(\boldsymbol{A})$ 的基，可以证明 $\left\{\boldsymbol{B}_{\beta}\boldsymbol{y}_1,...,\boldsymbol{B}_{\beta}\boldsymbol{y}_{r}\right\}$ 也是 $\mathscr{R}(T)$ 的基. (自行练习)

---

求零空间与值空间的基与维数

例 $\mathbb{R}^{2 \times 2}$ 上的线性变换 $T$ 定义为

$$T \boldsymbol{X}=\boldsymbol{CX}-\boldsymbol{XC}, \quad \boldsymbol{X} \in \mathbb{R}^{2 \times 2},$$

其中 $\boldsymbol{C}=\left[\begin{array}{ll}{1} & {0} \\ {1} & {1}\end{array}\right]$ .

(1) 求 $T$ 的零度和零空间的基;

(2) 求 $T$ 的秩和值空间的基.

---

提示： 先求零度和秩

• 取 $\mathbb{R}^{2\times 2}$ 的基
  
  • $\boldsymbol{B}=\left\{\left[\begin{array}{ll}{1} & {0} \\ {0} & {0}\end{array}\right], \left[\begin{array}{ll}{0} & {1} \\ {0} & {0}\end{array}\right], \left[\begin{array}{ll}{0} & {0} \\ {1} & {0}\end{array}\right], \left[\begin{array}{ll}{0} & {0} \\ {0} & {1}\end{array}\right]\right\}$
• $T$ 在基 $\boldsymbol{B}$ 下的矩阵为 $\boldsymbol{A}=\left[\begin{array}{cccc}{0} & {-1} & {0} & {0} \\ {0} & {0} & {0} & {0} \\ {1} & {0} & {0} & {-1} \\ {0} & {1} & {0} & {0}\end{array}\right]$
• $\mathrm{null}(T)=4-\mathrm{rank}(\boldsymbol{A})=2$
• $\mathrm{rank}(T)=\mathrm{rank}(\boldsymbol{A})=2$

---

求零空间的基

• 解出 $\boldsymbol{Ax}=\boldsymbol{0}$ 的基础解系：
  
  • $\boldsymbol{x}_{1}=\left[\begin{array}{llll}{0} & {0} & {1} & {0}\end{array}\right]^{\mathrm{T}}$,
  • $\boldsymbol{x}_{2}=\left[\begin{array}{llll}{1} & {0} & {0} & {1}\end{array}\right]^{\mathrm{T}}$
• 相应地，$\mathscr{N}(T)$ 的基
  
  • $\boldsymbol{\alpha}_{1}=\boldsymbol{Bx}_1=\left[\begin{array}{ll}{0} & {0} \\ {1} & {0}\end{array}\right]$，
  • $\boldsymbol{\alpha}_{2}=\boldsymbol{Bx}_2=\left[\begin{array}{ll}{1} & {0} \\ {0} & {1}\end{array}\right]$

---

求值空间的基

• 利用除列交换之外的初等列变换，将 $\boldsymbol{A}$ 化为最简列阶梯型，例如：$\left[\begin{array}{cccc}{0} & {-1} & {0} & {0} \\ {0} & {0} & {0} & {0} \\ {1} & {0} & {0} & {0} \\ {0} & {1} & {0} & {0}\end{array}\right]$ ，最后剩余的非零列对应于 $T\boldsymbol{B}$ 中的极大无关组
• $\mathscr{R}(T)$ 的基可以取为 $\left\{ T\left(\left[\begin{array}{cc}{1} & {0} \\ {0} & {0}\end{array}\right]\right),T\left(\left[\begin{array}{cc}{0} & {1} \\ {0} & {0}\end{array}\right]\right)\right\}$
  
  • 也即 $\left\{ \left[\begin{array}{cc}{0} & {0} \\ {1} & {0}\end{array}\right],\left[\begin{array}{cc}{-1} & {0} \\ {0} & {1}\end{array}\right]\right\}$

---

另一种解法

• 设 $\boldsymbol{X}=\begin{bmatrix}x_1 & x_2 \\ x_3 & x_4\end{bmatrix}$，其中 $x_1,x_2,x_3,x_4\in\mathbb{R}$.
• $T\boldsymbol{X}=\begin{bmatrix}1 & 0 \\ 1 & 1\end{bmatrix}\begin{bmatrix}x_1 & x_2 \\ x_3 & x_4\end{bmatrix}-\begin{bmatrix}x_1 & x_2 \\ x_3 & x_4\end{bmatrix}\begin{bmatrix}1 & 0 \\ 1 & 1\end{bmatrix}=\begin{bmatrix}-x_2 & 0 \\ x_1-x_4 & x_2\end{bmatrix}$
• 令 $T\boldsymbol{X}=\boldsymbol{0}$，解得 $x_2=0,\;x_1=x_4$
• 由此可取 $\left\{\begin{bmatrix}0 & 0 \\ 1 & 0\end{bmatrix},\;\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}\right\}$ 为 $T\boldsymbol{X}=\boldsymbol{0}$ 的基础解系，也即 $\mathscr{N}(T)$ 的基，进而 $\mathrm{null}(T)=2$.

---

• 又 $T\boldsymbol{X}=\begin{bmatrix}-x_2 & 0 \\ x_1-x_4 & x_2\end{bmatrix}=x_2\begin{bmatrix}-1 & 0 \\ 0 & 1\end{bmatrix}+(x_1-x_4)\begin{bmatrix}0 & 0 \\ 1 & 0\end{bmatrix}$
• 由此可知 $\mathscr{R}(T)$ 中的向量均可被 $\left\{\begin{bmatrix}-1 & 0 \\ 0 & 1\end{bmatrix},\;\begin{bmatrix}0 & 0 \\ 1 & 0\end{bmatrix}\right\}$ 线性表示，注意到该向量组线性无关，故其为 $\mathscr{R}(T)$ 的基.
• 进而 $\mathrm{rank}(T)=2$.

---

求零空间的基的一般步骤

设 $T$ 是 $V^n\to V^m$ 的线性变换，$V^n$ 与 $V^m$ 的基分别是

$$\boldsymbol{B}_{{\alpha}}=\left\{\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{n}\right\}, \boldsymbol{B}_{{\beta}}=\left\{\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2}, \cdots, \boldsymbol{\beta}_{m}\right\}$$

1. 求出 $T$ 在基偶 $\{\boldsymbol{B}_{{\alpha}},\boldsymbol{B}_{{\beta}}\}$ 下的矩阵 $\boldsymbol{A}$;
2. 求 $\boldsymbol{Ax}=\boldsymbol{0}$ 的基础解系： $\{\boldsymbol{x}_1,\boldsymbol{x}_2,\ldots,\boldsymbol{x}_{n-r}\}$;
3. $\{\boldsymbol{B}_{{\alpha}}\boldsymbol{x}_1,\boldsymbol{B}_{{\alpha}}\boldsymbol{x}_2,\ldots,\boldsymbol{B}_{{\alpha}}\boldsymbol{x}_{n-r}\}$ 即为 $\mathscr{N}(T)$ 的基.

---

求值空间的基的一般步骤

设 $T$ 是 $V^n\to V^m$ 的线性变换，$V^n$ 与 $V^m$ 的基分别是

$$\boldsymbol{B}_{{\alpha}}=\left\{\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \cdots, \boldsymbol{\alpha}_{n}\right\}, \boldsymbol{B}_{{\beta}}=\left\{\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2}, \cdots, \boldsymbol{\beta}_{m}\right\}$$

1. 求出 $T$ 在基偶 $\{\boldsymbol{B}_{{\alpha}},\boldsymbol{B}_{{\beta}}\}$ 下的矩阵 $\boldsymbol{A}$;
2. 利用除列交换外的初等列变换将 $\boldsymbol{A}$ 化为非零列最少的形式;
3. 在 $\boldsymbol{A}$ 化简得到的矩阵中，设非零列对应的列号为 $i_1,\ldots,i_r$，则 $\{T\boldsymbol{\alpha}_{i_1},\ldots,T\boldsymbol{\alpha}_{i_r}\}$ 即为 $\mathscr{R}(T)$ 的基.

---

补充例题

例 定义 $\mathbb{R}^n$ 上的线性变换 $T$

$$T \boldsymbol{\alpha}=\left[\begin{array}{ccccc} {0} & {0} & {\cdots} & {0} & {0} \\ {1} & {0} & {\cdots} & {0} & {0} \\ {0} & {1} & {\cdots} & {0} & {0} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} & {\vdots} \\ {0} & {0} & {\cdots} & {1} & {0} \end{array}\right] \boldsymbol{\alpha}, \quad \left(\boldsymbol{\alpha}\in \mathbb{R}^{n}\right)$$

(1) 证明对任意 $\boldsymbol{\alpha}\in \mathbb{R}^{n}$， $T^n\boldsymbol{\alpha}=\boldsymbol{0}$ ;

(2) 求 $T$ 的零空间和值空间的基与维数.

---

提示：(1) 证明 $T^n=0$

• 任取 $\boldsymbol{\alpha}=[x_1\;x_2\;\ldots\;x_n]^{\mathrm{T}}\in\mathbb{R}^n$
  
  • $T\boldsymbol{\alpha}=[0\;x_1\;\ldots\;x_{n-1}]^{\mathrm{T}}$
• 类推可知， $T^n\boldsymbol{\alpha}=\boldsymbol{0}$
• 注： 此时通常记 $T^n=0$
  
  • 此处的 $0$ 可以称为零变换，即任何向量在其作用下都将化为零向量
  • 类似地，常用 $I$ 表示恒等变换，即任何向量在其作用下都保持不变

---

提示：(2) 求 $T$ 的零空间和值空间的基与维数

• 取 $\mathbb{R}^n$ 的基 $\boldsymbol{\alpha}_{1}=\left[\begin{array}{l}{1} \\ {0} \\ {0} \\ {\vdots} \\ {0}\end{array}\right], \boldsymbol{\alpha}_{2}=\left[\begin{array}{c}{0} \\ {1} \\ {0} \\ {\vdots} \\ {0}\end{array}\right], \boldsymbol{\alpha}_{3}=\left[\begin{array}{c}{0} \\ {0} \\ {1} \\ {\vdots} \\ {0}\end{array}\right], \cdots, \boldsymbol{\alpha}_{n}=\left[\begin{array}{c}{0} \\ {0} \\ {0} \\ {\vdots} \\ {1}\end{array}\right]$
• $T \boldsymbol{\alpha}_{1}=\boldsymbol{\alpha}_{2}, T \boldsymbol{\alpha}_{2}=\boldsymbol{\alpha}_{3}, T \boldsymbol{\alpha}_{3}=\boldsymbol{\alpha}_{4}, \cdots, T \boldsymbol{\alpha}_{n-1}=\boldsymbol{\alpha}_{n}, T \boldsymbol{\alpha}_{n}=\boldsymbol{0}$
• $\{\boldsymbol{\alpha}_2,\boldsymbol{\alpha}_3,\ldots,\boldsymbol{\alpha}_n\}$ 线性无关，恰好构成 $\mathscr{R}(T)$ 的基，$\mathrm{rank}(T)=n-1$.
• $\mathrm{null}(T)=1$ ，而 $T\boldsymbol{\alpha}_n=\boldsymbol{0}$ ，故 $\{\boldsymbol{\alpha}_{n}\}$ 是 $\mathscr{N}(T)$ 的基.

---

例 设 $T$ 是 $V^4$ 上的线性变换， $T$ 在基 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\boldsymbol{\alpha}_3,\boldsymbol{\alpha}_4$ 下的矩阵为

$$\boldsymbol{A}=\left[\begin{array}{rrrr}{-1} & {2} & {1} & {3} \\ {1} & {0} & {2} & {1} \\ {1} & {2} & {5} & {5} \\ {2} & {-2} & {1} & {-2}\end{array}\right]$$

1. 求 $T$ 在 $\boldsymbol{\beta}_{1}=\boldsymbol{\alpha}_{1}-2 \boldsymbol{\alpha}_{2}+\boldsymbol{\alpha}_{4}, \boldsymbol{\beta}_{2}=3 \boldsymbol{\alpha}_{2}-\boldsymbol{\alpha}_{3}-\boldsymbol{\alpha}_{4},$ $\boldsymbol{\beta}_{3}=\boldsymbol{\alpha}_{3}+\boldsymbol{\alpha}_{4}, \boldsymbol{\beta}_{4}=2 \boldsymbol{\alpha}_{4}$ 下的矩阵;
2. 求 $T$ 的零空间和值空间的基与维数.

---

提示

• $\boldsymbol{B}_{{\beta}}=\boldsymbol{B}_{{\alpha}}\left[\begin{array}{rrrr}{1} & {0} & {0} & {0} \\ {-2} & {3} & {0} & {0} \\ {0} & {-1} & {1} & {0} \\ {1} & {-1} & {1} & {2}\end{array}\right]=\boldsymbol{B}_{{\alpha}}\boldsymbol{B}$
• $T\boldsymbol{B}_{{\beta}}=T\boldsymbol{B}_{{\alpha}}\boldsymbol{B}=\boldsymbol{B}_{{\alpha}}\boldsymbol{AB}=\boldsymbol{B}_{{\beta}}\boldsymbol{B}^{-1}\boldsymbol{AB}$

---

例 给定线性空间 $V$，且

$$W_1\oplus W_2=V,$$

证明：存在 $V$ 上的线性变换 $T$，使得

$$\mathscr{R}(T)=W_1,\;\;\mathscr{N}(T)=W_2.$$

---

提示

• 设 $\mathrm{dim}(V)=n,\;\mathrm{dim}(W_1)=r$.
• 取 $\{\boldsymbol{\alpha}_1,...,\boldsymbol{\alpha}_r\}$，$\{\boldsymbol{\alpha}_{r+1},...,\boldsymbol{\alpha}_n\}$ 分别为 $W_1,W_2$ 的基，则 $\boldsymbol{B}=\{\boldsymbol{\alpha}_1,...,\boldsymbol{\alpha}_n\}$ 是 $V^n$ 的基.
• 令 $\boldsymbol{A}=\left[\begin{array}{ll}\boldsymbol{I}_r & \\ & \boldsymbol{O}_{n-r}\end{array}\right]$，其中 $\boldsymbol{O}_{n-r}$ 表示 $n-r$ 阶零方阵.
• 令 $T\boldsymbol{B}=\boldsymbol{BA}$ ，即为所求.

---

例 设 $T_1,T_2$ 均为线性空间 $V$ 上的线性变换，满足

$$T_{1}^{2}=T_{1}, \quad T_{2}^{2}=T_{2}.$$

证明： $\mathscr{R}(T_1)=\mathscr{R}(T_2)$ 当且仅当

$$T_{1} T_{2}=T_{2}, \quad T_{2} T_{1}=T_{1}.$$

---

提示：必要性( $\Rightarrow$ )

• 已知 $\boldsymbol{R}=\mathscr{R}(T_1)=\mathscr{R}(T_2)$ ，设 $\{\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\ldots,\boldsymbol{\beta}_r\}$ 是 $\boldsymbol{R}$ 的基
• 记 $T_1\boldsymbol{\alpha}_i=\boldsymbol{\beta}_i,\;i=1,2,\ldots,r$ ，由 $T_1^2=T_1$ ， $T_1\boldsymbol{\beta}_i=T_1T_1\boldsymbol{\alpha}_i=T_1\boldsymbol{\alpha}_i=\boldsymbol{\beta}_i$ ，从而 $(T_1-I)\boldsymbol{\beta}_i=\boldsymbol{0}$ ， $i=1,2,\ldots,r$
• 同理可证 $T_2\boldsymbol{\beta}_i=\boldsymbol{\beta}_i,\;i=1,2,\ldots,r$
• $\forall\boldsymbol{\xi}\in V$ ，可记 $T_2\boldsymbol{\xi}=\sum\limits_{i=1}^rk_i\boldsymbol{\beta}_i$ ， $(T_1-I)T_2\boldsymbol{\xi}=\sum\limits_{i=1}^rk_i(T_1-I)\boldsymbol{\beta}_i=\boldsymbol{0}$
• 从而必有 $(T_1-I)T_2=0$ ，也即 $T_1T_2=T_2$

---

提示：充分性( $\Leftarrow$ )

• 设 $\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\ldots,\boldsymbol{\beta}_r$ 是 $\mathscr{R}(T_1)$ 的基，记 $T_1\boldsymbol{\alpha}_i=\boldsymbol{\beta}_i,\;i=1,2,\ldots,r$
• 由 $T_1^2=T_1$ ， $T_1\boldsymbol{\beta}_i=T_1T_1\boldsymbol{\alpha}_i=T_1\boldsymbol{\alpha}_i=\boldsymbol{\beta}_i$
• 由 $T_1=T_2T_1$ ， $\boldsymbol{\beta}_i=T_1\boldsymbol{\beta}_i=T_2T_1\boldsymbol{\beta}_i=T_2\boldsymbol{\beta}_i$
• $\forall\boldsymbol{\xi}\in V$ ，因 $T_1T_2\boldsymbol{\xi}\in\mathscr{R}(T_1)$ ，故可设 $T_1T_2\boldsymbol{\xi}=\sum\limits_{i=1}^rk_i\boldsymbol{\beta}_i$
• $T_2\boldsymbol{\xi}=T_1T_2\boldsymbol{\xi}=\sum\limits_{i=1}^rk_i\boldsymbol{\beta}_i$ ，由此即知 $\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\ldots,\boldsymbol{\beta}_r$ 也是 $\mathscr{R}(T_2)$ 的基

---

1.2.4 线性变换矩阵的相似化简

---

线性变换在不同基偶下的矩阵

假设 $T$ 是 $V^n\to V^m$ 的线性变换

• $\boldsymbol{B}_{{\alpha}},\boldsymbol{B}_{\tilde{{\alpha}}}$ 是 $V^n$ 的两组基， $\boldsymbol{B}_{{\beta}},\boldsymbol{B}_{\tilde{{\beta}}}$ 是 $V^m$ 的两组基
• $T\boldsymbol{B}_{{\alpha}}=\boldsymbol{B}_{{\beta}}\boldsymbol{A}$ ， $T\boldsymbol{B}_{\tilde{{\alpha}}}=\boldsymbol{B}_{\tilde{{\beta}}}\boldsymbol{B}$
• 设 $\boldsymbol{B}_{{\alpha}}$ 到 $\boldsymbol{B}_{\tilde{{\alpha}}}$ 的过渡矩阵是 $\boldsymbol{P}$ ，即 $\boldsymbol{B}_{\tilde{{\alpha}}}=\boldsymbol{B}_{{\alpha}}\boldsymbol{P}$
• 设 $\boldsymbol{B}_{{\beta}}$ 到 $\boldsymbol{B}_{\tilde{{\beta}}}$ 的过渡矩阵是 $\boldsymbol{Q}$ ，即 $\boldsymbol{B}_{\tilde{{\beta}}}=\boldsymbol{B}_{{\beta}}\boldsymbol{Q}$
• 则有 $\boldsymbol{A}=\boldsymbol{QBP}^{-1}$
• 可否通过选择适当的基偶，使得线性变换对应的矩阵具有比较简单的形式？

---

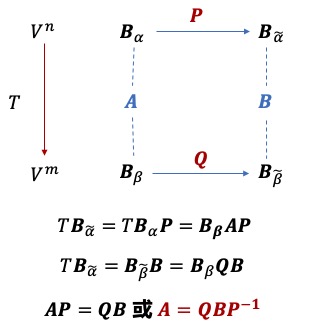
变换矩阵的相似关系

特别地，设 $T$ 是 $V^n\to V^n$ 的线性变换（此时称 $T$ 是 $V^n$ 上的线性变换），且取 $\boldsymbol{B}_{\beta}=\boldsymbol{B}_{\alpha}$，$\boldsymbol{B}_{\tilde{\beta}}=\boldsymbol{B}_{\tilde{\alpha}}$，则有 $\boldsymbol{P}=\boldsymbol{Q}$，进而

$$\boldsymbol{A}=\boldsymbol{PBP}^{-1}.$$

• 也即：$V^n$ 上的线性变换在不同基下对应的矩阵是相似（Similar）的.

---

线性变换的不变子空间

设 $T$ 是 $V^n$ 上的线性变换， $W$ 是 $V^n$ 的子空间，若对 $\forall\boldsymbol{\alpha}\in W$ 有 $T\boldsymbol{\alpha}\in W$ ，则称 $W$ 是 $T$ 的不变子空间 (Invariant Subspace)

• $T$ 的零空间 $\mathscr{N}(T)$ 和值空间 $\mathscr{R}(T)$ 都是 $T$ 的不变子空间

---

不变子空间的判定

引理 $W=\operatorname{span}\left\{\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \ldots, \boldsymbol{\alpha}_{r}\right\}$ 是 $T$ 的不变子空间，当且仅当：对任意 $i=1,2,...,r$，

$${T} \boldsymbol{\alpha}_{i} \in {W}.$$

---

不变子空间与分块对角阵

定理 $\boldsymbol{B}=\left\{\boldsymbol{\alpha}_{11}, \cdots, \boldsymbol{\alpha}_{1 n_{1}} , \boldsymbol{\alpha}_{21}, \cdots, \boldsymbol{\alpha}_{2 n_{2}} , \cdots , \boldsymbol{\alpha}_{s 1}, \cdots, \boldsymbol{\alpha}_{s n_{s}}\right\}$ 是 $V^n$ 的基，线性变换 $T$ 在 $\boldsymbol{B}$ 下的矩阵 $\boldsymbol{A}$ 是分块对角阵

$$\boldsymbol{A}=\operatorname{diag}\left\{\boldsymbol{A}_{1}, \boldsymbol{A}_{2}, \cdots, \boldsymbol{A}_{s}\right\}$$

其中 $\boldsymbol{A}_k$ 是 $n_k$ 阶方阵，$k=1,...,s$，当且仅当

$$W_{k}=\operatorname{span}\left\{\boldsymbol{\alpha}_{k 1}, \cdots, \boldsymbol{\alpha}_{k n_{k}}\right\} \quad(k=1,2, \cdots, s)$$

均是 $T$ 的不变子空间.

---

证明思路：必要性（ $\Rightarrow$ ）

• 设 ${T} \boldsymbol{B}=\left\{T \boldsymbol{\alpha}_{11}, \cdots, T \boldsymbol{\alpha}_{1 n_{1}} , \cdots , T \boldsymbol{\alpha}_{s 1} \cdots, T \boldsymbol{\alpha}_{s{n}_s}\right\}=\boldsymbol{BA}$
  
  • 其中 $\boldsymbol{A}=\operatorname{diag}\left\{\boldsymbol{A}_{1}, \boldsymbol{A}_{2}, \cdots, \boldsymbol{A}_{s}\right\}$，$\boldsymbol{A}_k=\left[a_{ij}^{(k)}\right]_{n_k\times n_k}$, $k=1,2,...,s$.
• 于是，对任意 $k=1,2,...,s$ 和 $j=1,...,n_k$，
  
  • $T \boldsymbol{\alpha}_{k j}=\sum_{i=1}^{n_k} a_{ij}^{(k)}\boldsymbol{\alpha}_{ki}$.
• 由此可知 $T \boldsymbol{\alpha}_{kj} \in W_{k}=\operatorname{span}\left\{\boldsymbol{\alpha}_{k1}, \cdots, \boldsymbol{\alpha}_{k n_{k}}\right\}$.
• 故 $W_k\;(k=1,...,s)$ 均为 $T$ 的不变子空间.

---

充分性（ $\Leftarrow$ ）：设 $W_k(k=1,...,s)$ 均是 $T$ 的不变子空间.

• 对任意 $k=1,2,...,s$ 和 $j=1,...,n_k$，存在 $a_{1j}^{(k)},...,a_{n_kj}^{(k)}$，使得 $T \boldsymbol{\alpha}_{k j}=\left\{\boldsymbol{\alpha}_{k 1}, \cdots, \boldsymbol{\alpha}_{k n_{k}}\right\}\left[\begin{array}{c}{a_{1 j}^{(k)}} \\ {\vdots} \\ {a_{n_k j}^{(k)}}\end{array}\right]$.
• $\boldsymbol{A}_k=\left[a_{ij}^{(k)}\right]_{n_k\times n_k}$, $k=1,2,...,s$.
  
  • 则 $T\left\{\boldsymbol{\alpha}_{k 1}, \cdots, \boldsymbol{\alpha}_{k n_{k}}\right\}=\left\{\boldsymbol{\alpha}_{k 1}, \cdots, \boldsymbol{\alpha}_{k n_{k}}\right\} \boldsymbol{A}_{k}$
• 进而 ${T} \boldsymbol{B}=\left\{T \boldsymbol{\alpha}_{11}, \cdots, T \boldsymbol{\alpha}_{1 n_{1}} , \cdots , T \boldsymbol{\alpha}_{s 1} \cdots, T \boldsymbol{\alpha}_{s n_{s}}\right\}=\boldsymbol{B}\,\mathrm{diag}\{\boldsymbol{A}_1,\boldsymbol{A}_2,...,\boldsymbol{A}_s\}$.

---

推论 设 $\boldsymbol{B}=\left\{\boldsymbol{\alpha}_{1}, \cdots, \boldsymbol{\alpha}_{n}\right\}$ 是 $V^n$ 的基，则 $T$ 在 $\boldsymbol{B}$ 下的矩阵 $\boldsymbol{A}$ 是对角阵

$$\boldsymbol{A}=\operatorname{diag}\left\{\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}\right\}$$

的充要条件是

$$T \boldsymbol{\alpha}_{i}=\lambda_{i} \boldsymbol{\alpha}_{i} \quad(i=1,2, \cdots, n).$$

---

提示

• $T\boldsymbol{B}=[T\boldsymbol{\alpha_1}\;T\boldsymbol{\alpha_2}\;...\;T\boldsymbol{\alpha_n}]$
  
  • $=[\lambda_1T\boldsymbol{\alpha_1}\;\lambda_2T\boldsymbol{\alpha_2}\;...\;\lambda_nT\boldsymbol{\alpha_n}]$
  • $=[\boldsymbol{\alpha_1}\;\boldsymbol{\alpha_2}\;...\;\boldsymbol{\alpha_n}]\begin{bmatrix}\lambda_1 \\ & \lambda_2 \\ && \ddots \\ &&& \lambda_n\end{bmatrix}$
  • $=\boldsymbol{B}\ \mathrm{diag}\left\{\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}\right\}$

---

1.2.5 线性变换的特征值与特征向量

设 $T$ 是 $V$ 上的线性变换，若存在 $\lambda\in F$ ，以及非零向量 $\boldsymbol{\xi}\in V$ ，使得

$$T\boldsymbol{\xi}=\lambda\boldsymbol{\xi}$$

则称 $\lambda$ 为 $T$ 的 特征值(Eigenvalue)，称 $\boldsymbol{\xi}$ 为 $T$ 关于 $\lambda$ 的 特征向量(Eigenvector)

• ${V}_{\lambda}=\left\{{\boldsymbol{\xi}} \in {V} | {T} {\boldsymbol{\xi}}=\lambda \boldsymbol{\xi}\right\}$ 是 $V$ 的子空间，称为 $T$ 关于特征值 $\lambda$ 的 特征子空间(Eigensubspace)，记为 $V_{\lambda}$
• $\mathrm{dim}V_{\lambda}$ 称为 $\lambda$ 的几何重数(Geometric Multiplicity)

---

线性变换的特征值和特征向量的基本性质

• 不同特征值对应的特征向量线性无关
• 不同特征值对应的特征子空间的和空间为直和
• $T$ 的特征子空间是它的不变子空间
• 设 $T$ 在基 $\boldsymbol{B}$ 下的矩阵为 $\boldsymbol{A}$，则
  
  • $\bbox[yellow]{\boldsymbol{Ax}=\lambda\boldsymbol{x}\quad\Leftrightarrow\quad T\boldsymbol{\boldsymbol{\xi}}=\lambda\boldsymbol{\xi},\;(\boldsymbol{\xi}=\boldsymbol{Bx})}$
  • 即：$T$ 和 $\boldsymbol{A}$ 具有相同的特征值，且特征向量一一对应.

---

线性变换的特征值和特征向量的求解步骤

• 任取 $V^n$ 的基 $\boldsymbol{B}=\{\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\ldots,\boldsymbol{\alpha}_n\}$；
• 计算 $T$ 在 $\boldsymbol{B}$ 下的矩阵(方阵) $\boldsymbol{A}$；
• 求出 $\boldsymbol{A}$ 的特征值 $\lambda_i$ 和对应的特征向量 $\boldsymbol{x}_i$；
• $\lambda_i$ 就是 $T$ 的特征值；
• $\boldsymbol{\beta}_i=\boldsymbol{B}\boldsymbol{x}_i$ 就是 $T$ 的与 $\lambda_i$ 对应的特征向量.

---

例 定义 $P_2(t)\to P_2(t)$ 的线性变换 $T$

$$T p(t)=p(t)+(t+1) \frac{\mathrm{d}}{\mathrm{d} t} p(t)$$

试求其特征值与特征向量.

---

提示

• 取 $P_2(t)$ 的基 $\boldsymbol{B}=\{1,t,t^2\}$ ， $T$ 在 $\boldsymbol{B}$ 下的矩阵 $\boldsymbol{A}=\left[\begin{array}{lll}{1} & {1} & {0} \\ {0} & {2} & {2} \\ {0} & {0} & {3}\end{array}\right]$.
• $\boldsymbol{A}$ 的特征值： $\lambda_{1}=1, \lambda_{2}=2, \lambda_{3}=3$ ，即 $T$ 的特征值.
• $\boldsymbol{A}$ 的特征向量：
  
  • $\boldsymbol{x}_{1}=[1 \quad 0 \quad 0]^{\mathrm{T}}, \quad \boldsymbol{x}_{2}=[1 \quad 1 \quad 0]^{\mathrm{T}}, \quad \boldsymbol{x}_{3}=[1 \quad 2 \quad 1]^{\mathrm{T}}$.
• $T$ 的特征向量：$\boldsymbol{\xi}_{1}=\boldsymbol{B}\boldsymbol{x}_{1}=1,\quad\boldsymbol{\xi}_{2}=\boldsymbol{B} \boldsymbol{x}_{2}=1+t$，$\boldsymbol{\xi}_{3}=\boldsymbol{B} \boldsymbol{x}_{3}=1+2t+t^2$.

---

1.2.6 线性变换的对角化

设 $T$ 是 $V^n$ 上的线性变换，若存在 $V^n$ 上的一个基 $\boldsymbol{B}$ ，使得 $T$ 在该基下的矩阵是对角阵，则称 $T$ 可对角化 (Diagonalizable).

• 定理 $T$ 可对角化，当且仅当下列等价条件之一成立

  1. $T$ 有 $n$ 个线性无关的特征向量;
  2. $n=\sum\limits_{i=1}^s\dim V_{\lambda_i}$，其中 $\lambda_i,i=1,2,...,s$ 是 $T$ 的全部特征值.

• 推论 设 $T$ 是 $V^n$ 上的线性变换，若 $T$ 可有 $n$ 个不同的特征值，则 $T$ 可对角化.

---

可对角化的判定

例 设 $\boldsymbol{B}=\{\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\boldsymbol{\alpha}_3\}$ 是 $V^3$ 的基， $T$ 是 $V^3$ 上的线性变换， $T$ 在基 $\boldsymbol{B}$ 下的矩阵为

$$\boldsymbol{A}=\left[\begin{array}{rrr} {0} & {1} & {0} \\ {-4} & {4} & {0} \\ {-2} & {1} & {2} \end{array}\right]$$

试判断， $T$ 是否可对角化？

---

解：

$$|\lambda \boldsymbol{I}-\boldsymbol{A}|=\left|\begin{array}{ccc}{\lambda} & {-1} & {0} \\ {4} & {\lambda-4} & {0} \\ {2} & {-1} & {\lambda-2}\end{array}\right|=(\lambda-2)^{3}$$

所以 $T$ 的特征值为 $\lambda=2$ （三重根）.

又 $\operatorname{rank}(2 \boldsymbol{I}-\boldsymbol{A})=1$，故 $\operatorname{dim} V_{\lambda}=2<3$ ，所以 $T$ 不可对角化.

---

对角化的计算过程

例 定义线性变换 $T: \boldsymbol{TX}=\boldsymbol{XC}, \forall \boldsymbol{X}\in\mathbb{R}^{2\times 2}$ ，其中

$$\boldsymbol{C}=\left[\begin{array}{ll}{1} & {1} \\ {1} & {1}\end{array}\right]$$

(1) 求 $T$ 的特征值与特征向量；

(2) 判断 $T$ 是否可对角化？若能对角化，试求 $\mathbb{R}^{2\times 2}$ 的基 $\boldsymbol{B}$ , 使得 $T$ 在 $\boldsymbol{B}$ 下的矩阵是对角阵。

---

提示：

• 取 $\mathbb{R}^{2\times 2}$ 的基 $\boldsymbol{B}_{{\alpha}}=\{\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\boldsymbol{\alpha}_3,\boldsymbol{\alpha}_4\}=\left\{\left[\begin{array}{ll}{1} & {0} \\ {0} & {0}\end{array}\right], \left[\begin{array}{ll}{0} & {1} \\ {0} & {0}\end{array}\right], \left[\begin{array}{ll}{0} & {0} \\ {1} & {0}\end{array}\right], \left[\begin{array}{ll}{0} & {0} \\ {0} & {1}\end{array}\right]\right\}$.
• 求出 $T$ 在 $\boldsymbol{B}_{{\alpha}}$ 下的矩阵 $\boldsymbol{A}=\left[\begin{array}{llll}{1} & {1} & {0} & {0} \\ {1} & {1} & {0} & {0} \\ {0} & {0} & {1} & {1} \\ {0} & {0} & {1} & {1}\end{array}\right]$.

---

• $|\lambda \boldsymbol{I}-\boldsymbol{A}|=\left|\begin{array}{cccc}{\lambda-1} & {-1} & {0} & {0} \\ {-1} & {\lambda-1} & {0} & {0} \\ {0} & {0} & {\lambda-1} & {-1} \\ {0} & {0} & {-1} & {\lambda-1}\end{array}\right|=\lambda^{2}(\lambda-2)^{2}$
• 求得 $\boldsymbol{A}$ 的特征值： $\lambda_{1}=\lambda_{2}=0, \quad \lambda_{3}=\lambda_{4}=2$
• 进一步求得对应的特征向量
  
  • $\boldsymbol{x}_{1}=[1\;\;-1\;\;0\;\;0]^{\mathrm{T}},\; \boldsymbol{x}_{2}=[0\;\;0\;\;1\;\;-1]^{\mathrm{T}},$
  • $\boldsymbol{x}_{3}=[1\;\;1\;\;0\;\;0]^{\mathrm{T}},\; \boldsymbol{x}_{4}=[0\;\;0\;\;1\;\;1]^{\mathrm{T}}$

---

• 进而，$T$ 的特征向量
  
  • $\boldsymbol{\beta}_{1}=\boldsymbol{B}_{{\alpha}}\boldsymbol{x}_1=\left[\begin{array}{rr}{1} & {-1} \\ {0} & {0}\end{array}\right], \boldsymbol{\beta}_{2}=\boldsymbol{B}_{{\alpha}}\boldsymbol{x}_2=\left[\begin{array}{rr}{0} & {0} \\ {1} & {-1}\end{array}\right]$
  • $\boldsymbol{\beta}_{3}=\boldsymbol{B}_{{\alpha}}\boldsymbol{x}_3=\left[\begin{array}{ll}{1} & {1} \\ {0} & {0}\end{array}\right], \quad \boldsymbol{\beta}_{4}=\boldsymbol{B}_{{\alpha}}\boldsymbol{x}_4=\left[\begin{array}{ll}{0} & {0} \\ {1} & {1}\end{array}\right]$
• 因为 $T$ 有四个线性无关的特征向量，所以可对角化
• $T$ 在基 $\left\{\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2}, \boldsymbol{\beta}_{3}, \boldsymbol{\beta}_{4}\right\}$ 下的矩阵为 $\left[\begin{array}{llll}{0} & {0} & {0} & {0} \\ {0} & {0} & {0} & {0} \\ {0} & {0} & {2} & {0} \\ {0} & {0} & {0} & {2}\end{array}\right]$.

---

例 已知 $\boldsymbol{B}=\left[\begin{array}{ll}{1} & {1} \\ {0} & {1}\end{array}\right]$ ，线性空间

$$V=\left\{\left[\begin{array}{ll}{a_{11}} & {a_{12}} \\ {a_{21}} & {a_{22}}\end{array}\right] \in \mathbb{R}^{2 \times 2} \bigg| a_{11}+a_{22}=0\right\},$$

定义 $V$ 上的线性变换 $T$ 为

$$T \boldsymbol{X}=\boldsymbol{B}^{\mathrm{T}} \boldsymbol{X}-\boldsymbol{X}^{\mathrm{T}} \boldsymbol{B}, \quad \boldsymbol{X} \in \mathbb{R}^{2 \times 2}$$

能否找到 $V$ 上的一组基 $\boldsymbol{B}_{{\beta}}$ ，使得 $T$ 在 $\boldsymbol{B}_{{\beta}}$ 下为对角阵？

---

提示

• 取 $V$ 的基 $\boldsymbol{B}_{{\alpha}}=\{\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\boldsymbol{\alpha}_3\}=\left\{\left[\begin{array}{cc}{1} & {0} \\ {0} & {-1}\end{array}\right], \; \left[\begin{array}{cc}{0} & {0} \\ {1} & {0}\end{array}\right], \; \left[\begin{array}{cc}{0} & {1} \\ {0} & {0}\end{array}\right]\right\}$
• 求得 $T$ 在 $\boldsymbol{B}_{{\alpha}}$ 下的矩阵 $\boldsymbol{A}=\left[\begin{array}{ccc}{0} & {0} & {0} \\ {1} & {1} & {-1} \\ {-1} & {-1} & {1}\end{array}\right]$

---

• 令 $|\lambda \boldsymbol{I}-\boldsymbol{A}|=\left|\begin{array}{ccc}{\lambda} & {0} & {0} \\ {-1} & {\lambda-1} & {1} \\ {1} & {1} & {\lambda-1}\end{array}\right|=\lambda^{2}(\lambda-2)=0$
• 解得 $\boldsymbol{A}$ 的特征值： $\lambda_{1}=\lambda_{2}=0, \; \lambda_{3}=2$
• 进一步求得对应的特征向量：$\boldsymbol{x}_1=\begin{bmatrix}1\\ 0 \\ 1\end{bmatrix},\;\boldsymbol{x}_2=\begin{bmatrix}0\\ 1 \\ 1\end{bmatrix},\;\boldsymbol{x}_3=\begin{bmatrix}0\\ 1 \\ -1\end{bmatrix}$

---

• 令 $\boldsymbol{P}=\left[\begin{array}{lll}{\boldsymbol{x}_{1}} & {\boldsymbol{x}_{2}} & {\boldsymbol{x}_{3}}\end{array}\right]=\left[\begin{array}{ccc}{1} & {0} & {0} \\ {0} & {1} & {1} \\ {1} & {1} & {-1}\end{array}\right]$
• 取基 $\boldsymbol{B}_{{\beta}}=\boldsymbol{B}_{{\alpha}}\boldsymbol{P}=\left\{\begin{bmatrix}1 & 1 \\ 0 & -1\end{bmatrix},\begin{bmatrix} 0 & 1 \\ 1 & 0\end{bmatrix},\begin{bmatrix} 0 & -1 \\ 1 & 0\end{bmatrix}\right\}$
• 则 $T$ 在 $\boldsymbol{B}_{{\beta}}$ 下的矩阵为 $\boldsymbol{C}=\boldsymbol{P}^{-1} \boldsymbol{A P}=\left[\begin{array}{lll}{0} & {0} & {0} \\ {0} & {0} & {0} \\ {0} & {0} & {2}\end{array}\right]$.

---

小结

• 线性变换的定义与判定
• 线性变换的矩阵表示
  
  • 不同基偶之下的矩阵之间的关系
• 不变子空间
  
  • 零空间与值空间
  • 特征子空间
• 线性变换的对角化 $\Leftrightarrow$ 对应矩阵的相似对角化

---

投影变换的特征值与特征向量

设 $V=V_1\oplus V_2$，定义投影变换如下：对任意 $\boldsymbol{\xi}\in V$，有唯一分解式 $\boldsymbol{\xi}=\boldsymbol{\alpha}+\boldsymbol{\beta}$，其中 $\boldsymbol{\alpha}\in V_1$，$\boldsymbol{\beta}\in V_2$，$T\boldsymbol{\xi}=\boldsymbol{\alpha}$.

• $T$ 具有两个特征值 $0,1$
• $\forall\boldsymbol{\alpha}\in V_1$，$T\boldsymbol{\alpha}=\boldsymbol{\alpha}$：$V_1$ 是 $T$ 的特征值 $1$ 对应的特征子空间
• $\forall\boldsymbol{\beta}\in V_2$，$T\boldsymbol{\beta}=\boldsymbol{0}$：$V_2$ 是 $T$ 的特征值 $0$ 对应的特征子空间
• 注： 投影变换也称为幂等变换，既：$T(T\boldsymbol{\xi})=T\boldsymbol{\xi},\;(\forall\boldsymbol{\xi}\in V)$

---

补充例题

例 设 $T$ 是线性空间 $V^3$ 上的线性变换，其在基 $\{\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\boldsymbol{\alpha}_3\}$ 下的矩阵为

$$\boldsymbol{A}=\left[\begin{array}{rrr} {1} & {a} & {b} \\ {} & {1} & {c} \\ {} & {} & {-1} \end{array}\right]$$

给出 $T$ 可相似对角化的条件，并在此条件下求 $V^3$ 的一个基，使得 $T$ 在该基下的矩阵是对角阵.

---

提示

• $\boldsymbol{A}$ 的特征值： $\lambda_1=\lambda_2=1,\lambda_3=-1$
• $\boldsymbol{A}-\boldsymbol{I}=\left[\begin{array}{rrr}{0} & {a} & {b} \\ {} & {0} & {c} \\ {} & {} & {-2} \end{array}\right]\to\left[\begin{array}{ccc}{0} & {a} & {0} \\ {} & {0} & {1} \\ {} & {} & {0} \end{array}\right]$
  
  • $a=0$ 时 $\boldsymbol{A}$ 可对角化
  • 特征向量： $\boldsymbol{x}_1=[1\;\;0\;\;0]^{\mathrm{T}},\boldsymbol{x}_2=[0\;\;1\;\;0]^{\mathrm{T}}$
• $\boldsymbol{A}+\boldsymbol{I}=\left[\begin{array}{ccc}{2} & {0} & {b} \\ {} & {2} & {c} \\ {} & {} & {0} \end{array}\right]\to\left[\begin{array}{ccc}{1} & {0} & {b/2} \\ {} & {1} & {c/2} \\ {} & {} & {0} \end{array}\right]$
  
  • 特征向量： $\boldsymbol{x}_3=[b\quad c\;-2]^{\mathrm{T}}$

---

例 设 $T$ 是线性空间 $V^n$ 上的线性变换，其在基 $\{\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\ldots,\boldsymbol{\alpha}_n\}$ 下的矩阵为

$$\boldsymbol{A}=\left[\begin{array}{ccccc} {\lambda} & {1} & {} & {} & {} \\ {} & {\lambda} & {\ddots} & {} & {} \\ & & {\ddots} & {\ddots}\\ {} & {} & {} & {\lambda} & {1} \\ {} & {} & {} & {} & {\lambda} \end{array}\right]$$

1. 证明 $\boldsymbol{\alpha}_1$ 属于 $T$ 的任意一个非零不变子空间;
2. 证明 $V^n$ 不能分解成为 $T$ 的两个非零不变子空间的直和.

---

提示

• 证明对任意 $i=1,2,\ldots,n$ ， $\mathrm{span}\{\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\ldots,\boldsymbol{\alpha}_i\}$ 都是 $T$ 的不变子空间
• 证明任意不含 $\boldsymbol{\alpha}_1$ 的向量组 $\{\boldsymbol{\alpha}_{i_1},\boldsymbol{\alpha}_{i_2},\ldots,\boldsymbol{\alpha}_{i_m}\}$, $(1< i_1<i_2<\ldots<i_m\leq n)$ 所张成的空间都不是 $T$ 的不变子空间
  
  • 事实上， $T\boldsymbol{\alpha}_{i_1}=\boldsymbol{\alpha}_{i_1-1}+\lambda\boldsymbol{\alpha}_{i_1}$ 无法被 $\{\boldsymbol{\alpha}_{i_1},\ldots,\boldsymbol{\alpha}_{i_m}\}$ 线性表出
• 设 $W$ 是 $T$ 的非零不变子空间，取它的基 $\{\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\ldots,\boldsymbol{\beta}_s\}$
• 证明 $\{\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\ldots,\boldsymbol{\beta}_s\}$ 必可以被某一组 $\{\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\ldots,\boldsymbol{\alpha}_r\}$ 线性表出

---

• 显然 $W$ 是 $\mathrm{span}\{\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\ldots,\boldsymbol{\alpha}_r\}$ 的不变子空间
• 记 $W=\mathrm{span}\{\boldsymbol{\alpha}_{i_1},\boldsymbol{\alpha}_{i_2},\ldots,\boldsymbol{\alpha}_{i_m}\}$,
  
  • $(1\leq i_1<i_2<\ldots<i_m\leq r)$
• 若 $\{\boldsymbol{\alpha}_{i_1},\boldsymbol{\alpha}_{i_2},\ldots,\boldsymbol{\alpha}_{i_m}\}$ 中不包含 $\boldsymbol{\alpha}_1$ ，则 $\mathrm{span}\{\boldsymbol{\alpha}_{i_1},\boldsymbol{\alpha}_{i_2},\ldots,\boldsymbol{\alpha}_{i_m}\}$ 不是 $T$ 的不变子空间
• 因此，必有 $\boldsymbol{\alpha}_1\in W$
• 任取 $T$ 的两个非零不变子空间 $W_1,W_2$ ，必有 $\boldsymbol{\alpha}_1\in W_1\cap W_2$ ，故 $W_1+W_2$ 不是直和