7.1 参数假设检验

高等工程数学 讲义 2024AU

---

---

第七章 假设检验

---

假设检验关注的问题

提出某种假设，然后利用统计数据判断其真伪.

• 需要回答的问题：
  
  1. 如何（定量地）表达假设？
  2. 真伪的标准是什么？
  3. 用什么样的方法进行判定？
  4. 如何理解检验的结果？

---

两类假设检验问题

1. 参数假设检验
   
   • 总体分布形式 $F(x; \theta)$ 已知，对总体分布中的参数 $\theta$ 进行检验.
   • 例如：次品率(均值检验)、质量对比(方差检验)、...
2. 非参数假设检验
   
   • 总体的分布未知，对总体的分布或总体间的关系进行检验.
   • 例如：判断总体的分布(拟合优度检验)、判断两随机变量是否独立(独立性检验)、...

---

7.1 参数假设检验

---

7.1.1 基本概念

例（产品质量检验） 某车间用一台自动包装机装化肥，每袋的标称重量规定为 $50$ kg. 某日开工后随机抽检 $9$ 袋产品，测得净重如下(单位:kg)

$$49.6, 48.4, 50, 48.6, 50.6, 49.8, 50.2, 49.2, 49.$$

设每袋化肥的实际重量服从正态分布，标准差为 $0.75$ kg，试问该日包装机工作是否正常？

---

统计推断的出发点

• 理论上讲，只有完整地了解了整个总体之后，才能对其有关特性做出准确无误的判断，但这在实际中常常是不可能的.
• 很多情况下，只能根据样本进行 推断.
• 由于样本未必能够严格反映总体的完整特征，最终推理得到的结论也可能是错误的！
• 因此，统计推断的结果，只能说是在一定的概率下正确.

---

例（产品质量检验） 某车间用一台自动包装机装化肥，每袋的标称重量规定为 $50$ kg. 某日开工后随机抽检 $9$ 袋产品，测得净重如下(单位:kg)

$$49.6, 48.4, 50, 48.6, 50.6, 49.8, 50.2, 49.2, 49.$$

设每袋化肥的实际重量服从正态分布，标准差为 $0.75$ kg，试问该日包装机工作是否正常？

• 分析： 样本均值 $\overline{x}=49.489<50$.
• 从以上的数据来看，均值(平均重量)没有达标.
• 疑问： 考虑到设备和测量可能存在的误差，这样的结果是否一定不可接受？

---

提出假设检验问题

• 已知条件：每袋化肥重量的分布 $N(\mu,(0.75)^2)$，理论上，包装机工作正常，当且仅当 $\mu=50$.
• 待检验的假设
  
  • 原假设（零假设，Null Hypothesis）：$H_0$：$\mu=50$，即：包装机工作正常
  • 备择假设（Alternative Hypothesis）：$H_1$：$\mu\ne 50$，即：包装机工作不正常
• 可能的结论
  
  • 拒绝 $H_0$，认为包装机工作不正常.
  • 接受 $H_0$，认为包装机工作正常.

---

假设检验的思想出发点

• 小概率事件在一次试验中是不会发生的.
• 统计推断的目的应该是证伪，即证明备择假设成立.
  
  • 不能证伪，则接受原假设.
• “接受”或“拒绝”一个假设，并不是要从逻辑或理论上“证明”或“证否”该命题，而只是基于给定的样本对该命题给出一种态度或处理行为上的判断.
  
  • 由于样本是随机的，因此作出的判断可能错误，假设检验的方法应该将犯错误的概率控制在可接受的范围内.

---

错误与风险

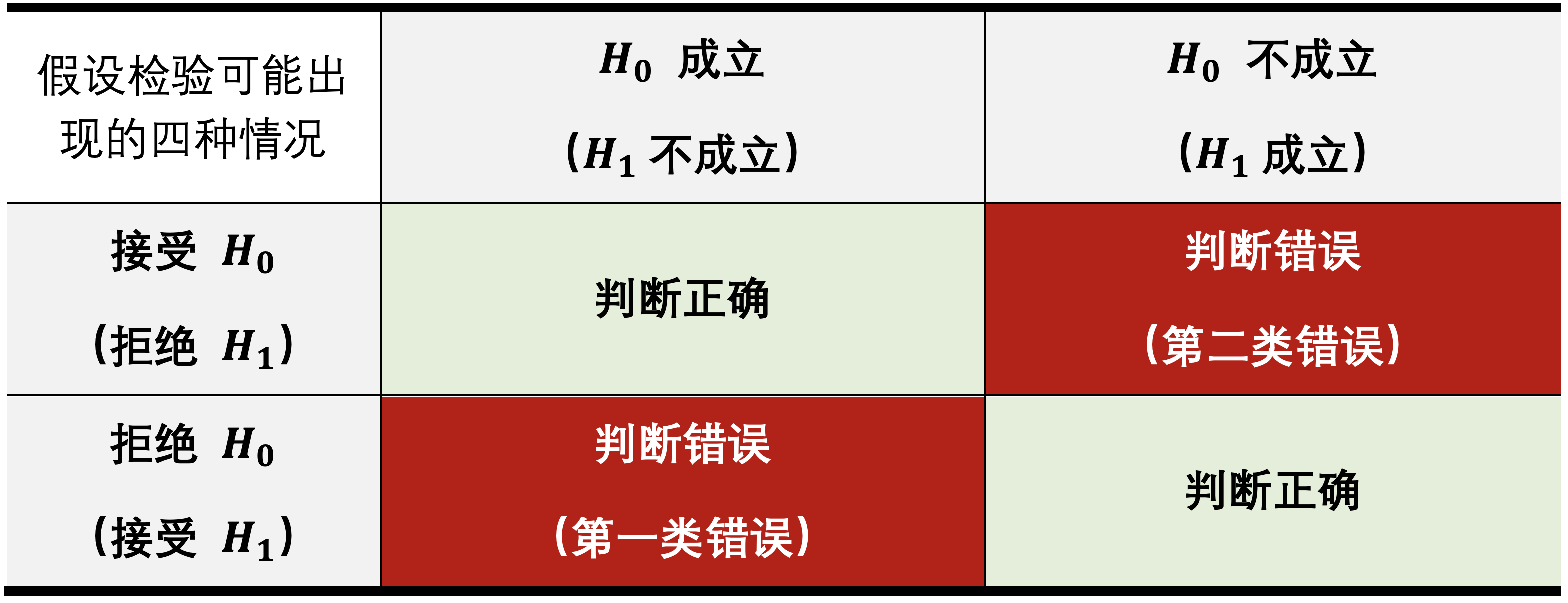
• I 类错误 (False Negative) $H_0$ 为真，却拒绝 $H_0$，
  
  • I 类风险： $P\{\text{拒绝}H_0| H_0\text{为真}\}$
• II 类错误 (False Positive) $H_0$ 为假，却接受 $H_0$
  
  • II 类风险： $P\{\text{接受}H_0| H_1\text{为真}\}$

---

产品质量检验问题的分析

• 提出假设： $H_0:\;\mu=\mu_0=50;\quad H_1:\; \mu\ne\mu_0=50$.
  
  • 根据所获得的样本观测值，决定是否接受 $H_0$.
• 分析：因为 $\mu$ 的无偏估计是 $\overline{X}$，也即 $\mu\approx\overline{x}$.
  
  • 若 $H_0$ 成立，$\left|\overline{x}-\mu_{0}\right|$ 应该较小. 反之，若 $\left|\overline{x}-\mu_{0}\right|$ 较大，则有理由认为 $H_0$ 不成立
• 检验规则：确定某个阈值 $C$
  
  • 当 $\left|\overline{x}-\mu_{0}\right|>C$ 时，拒绝原假设 $H_0$. 当 $\left|\overline{x}-\mu_{0}\right|\leq C$ 时，接受原假设 $H_0$
• 问题：如何确定 $C$？

---

假设检验原则

• 检验原则一：不轻易拒绝原假设，除非有极其充足的理由.
  
  • 即：犯 I 类错误的概率要足够小.
  • 对给定的 $\alpha\in(0,1)$ (显著性水平, Level of Significance),
  • 使得: $\bbox[yellow]{P\{\text{拒绝}H_0| H_0\text{为真}\}\leq\alpha.}$
• 检验原则二： 在满足原则一的条件下，使 II 类风险尽可能小.

---

产品质量检验

分析：根据题设，需要检验假设

$$H_0:\;\mu=\mu_0;\quad H_1:\; \mu\ne\mu_0$$

• 总体均值 $\mu$ 的无偏估计是 $\overline{X}$.
• 若 $H_0$ 成立，则 $|\overline{x}-\mu_0|$ 应较小.
• 若 $|\overline{x}-\mu_0|$ 偏大，则有理由认为 $H_0$ 不成立.
  
  • 即当 $|\overline{x}-\mu_0|\geq C$ 时，则认为 $H_0$ 不成立.

---

• 根据假设检验原则一
  
  • $\bbox[yellow]{P\{\text{拒绝}H_0| H_0\text{为真}\}\leq\alpha}$
  • $\Leftrightarrow P\left\{\left|\overline{X}-\mu_{0}\right| \geq C \bigg| \mu=\mu_{0}\right\} \leq \alpha$
  • $\Leftrightarrow P\left\{\left|\displaystyle \frac{\overline{X}-\mu_{0}}{\sigma / \sqrt{n}}\right| \geq \dfrac{C}{\sigma / \sqrt{n}} \bigg| \mu=\mu_{0}\right\} \leq \alpha$

• $H_0$ 成立时，$X\sim N(\mu_0,\sigma^2)$，故 $\displaystyle \frac{\overline{X}-\mu_{0}}{\sigma / \sqrt{n}}\sim N(0,1)$

• 任取 $C\geq\displaystyle \frac{\sigma}{\sqrt n}u_{1-\alpha/2}$ 即可满足假设检验原则一.

---

解：检验假设

$$H_0:\;\mu=\mu_0=50;\quad H_1:\; \mu\ne\mu_0=50.$$

拒绝域（即拒绝的条件）为

$$W_1=\left\{(x_1,x_2,...,x_n)\bigg|\left|\overline{x}-\mu_{0}\right| \geq C=\frac{\sigma}{\sqrt{n}} u_{1-\alpha / 2}\right\}.$$

取 $\alpha=0.05$，计算得到: $\overline{x}=49.489$, $C=0.49$.

因为 $|\overline{x}-\mu_0|=0.511>0.49$，即 $(x_1,x_2,...,x_n)\in W_1$，故应拒绝 $H_0$，也即认为今天的设备运转不正常.

---

设备真的不正常吗？

• 准确的结论：认为设备运行不正常而实际设备运行正常的可能性不超过 $5\%$.
• 不拒绝原假设可能有两种含义:
  
  1. 原假设的确是正确的，应当接受.
  2. 样本提供的信息不足以拒绝原假设，只好保留原假设.
• 从这个意义上说，假设检验的基本原则可以理解为：优先保护（不随意否定）原假设.

---

司法中的“无罪推定原则” (Presumption of Innocence)

• “未经人民法院依法判决，对任何人都不得确定有罪”
• 控方需要列举证据证明嫌疑人有罪.
• 如果证据确凿，则推翻无罪假设，嫌疑人被判有罪.
• 如果证据不足，则维持无罪判定，宣布嫌疑人无罪.
  
  1. 关在监狱中的人基本上都是有罪的.
  2. 监狱外面的人并不全是好人!

---

假设检验的基本步骤

1. 提出待检验的假设：原假设 $H_0$ vs 备择假设 $H_1$.
2. 分析得到拒绝域的形式.
3. 选择 检验统计量，根据显著性水平确定拒绝域.
4. 根据样本数据进行计算，作出判断.

---

注：1. 待检验的假设

$$\bbox[yellow]{H_0:\theta\in\Theta_0,\quad H_1:\theta\in\Theta_1.}$$

• 其中 $\Theta_0\cap\Theta_1=\varnothing$，但不要求一定有 $\Theta_0\cup\Theta_1=\Theta$.
• 如果 $\Theta_0$(或 $\Theta_1$) 只含有一个点，则对应假设称为 简单假设，否则称为 复合假设.
• 注意：
  
  1. 原假设中须包含等号.
  2. 通常情况下，应该将不应该/不希望轻易加以否定的假设作为原假设.
  3. 在保护倾向不明的情况下，一般选择与事实相反的命题作为原假设.

---

单边假设与双边假设

• 设原假设为 $H_0:\theta=\theta_0$，可能的备择假设通常有三种
  
  1. $H_1':\theta\ne\theta_0.$
  2. $H_1'':\theta<\theta_0.$
  3. $H_1''':\theta>\theta_0.$
• $H_0$ vs $H_1'$ 称为 双侧(边)假设.
• $H_0$ vs $H_1''$ 或 $H_0$ vs $H_1'''$ 称为 单侧(边)假设.

---

注：2. 拒绝域

• 假设检验等价于把样本空间划分为两个不相交的部分 $W_1$ 和 $\overline{W}_1$，其中 $W_1$ 称为 拒绝域 (Rejection Region).
• 当样本 $(x_1,...,x_n)\in W_1$ 时，则拒绝 $H_0$，否则接受 $H_0$.
• 拒绝域确定了，检验的判断准则也就确定了.
• 假设检验就是要证伪（尝试证明备择假设），因此拒绝域的形式完全由备择假设决定.

---

注：3. 检验统计量

• 结合总体信息，选择合适的检验统计量.
• 根据对 I 类风险的要求，由检验统计量的分布确定分位点.
• 检验统计量不具有唯一性，拒绝域也不具有唯一性.

---

注：4. 检验的结论

• 不同的显著性水平可能意味着不同的检验结论.
  
  • 通常情况下，显著性水平越高，拒绝域越大
• 注意：交换原假设和备择假设可能导致判断的结论相反.

---

例：交换原假设和备择假设（1）

某工厂规定特定产品的质量不能低于 $50$ kg，否则视为不合格. 已知该产品的质量服从 $N(\mu,0.25)$. 现抽检 100 件样品，测得样本均值 $\overline{x}=50.05$，试判断该批产品是否达到质量标准. $(\alpha=0.05)$

• $\bbox[lightgreen]{H_0:\mu\geq 50,\quad H_1:\mu<50}$
• 拒绝域 $W_1=\left\{(x_1,x_2,...,x_n)\big|\overline{x}<\mu_0+u_{\alpha}\displaystyle \frac{\sigma}{\sqrt{n}}=49.91\right\}$.
• 结论：接受 $H_0$，认为该批产品合格.

---

例：交换原假设和备择假设（2）

某工厂规定特定产品的质量不能低于 $50$ kg，否则视为不合格. 已知该产品的质量服从 $N(\mu,0.25)$. 现抽检 100 件样品，测得样本均值 $\overline{x}=50.05$，试判断该批产品是否达到质量标准. $(\alpha=0.05)$

• $\bbox[lightblue]{H_0:\mu\leq 50,\quad H_1:\mu>50}$
• 拒绝域 $W'_1=\left\{(x_1,x_2,...,x_n)\big|\overline{x}>\mu_0+u_{1-\alpha}\displaystyle \frac{\sigma}{\sqrt{n}}=50.08\right\}$
• 结论：接受 $H_0$，认为该批产品不合格.

---

检验的 p 值

例 某厂生产的合金强度服从正态分布 $N(\mu,16)$，其中的设计值为不低于 $110$ (Pa). 为保证质量，该厂每天都要对生产情况做例行检查，以判断生产是否正常进行. 某天从生产的产品中随机抽取 $25$ 块合金，测得其强度值均值为 $\overline{x}=108.2$ (Pa)，问当日生产是否正常？

• $H_0:\mu\geq 110,\quad H_1:\mu<110$
• $W_1=\left\{(x_1,x_2,...,x_n)\big|u=\displaystyle \frac{\overline{x}-110}{\sqrt{16}/\sqrt{25}} < u_{\alpha}\right\}$
• 观测结果 $u=-2.25$.

---

不同显著性水平之下的检验结论

$$\boxed{\begin{array}{c|cc} \quad \quad \text{显著性水平} \quad \quad & \quad \quad \text{拒绝域} \quad \quad & \quad \quad \text{对应的结论}(u=-2.25)\quad \quad \\ \hline \alpha=0.1 & u\leq -1.282 & \text{拒绝}H_0\\ \alpha=0.05 & u\leq -1.645 & \text{拒绝}H_0\\ \alpha=0.025 & u\leq -1.96 & \text{拒绝}H_0\\ \alpha=0.01 & u\leq -2.326 & \text{接受}H_0\\ \alpha=0.005 & u\leq -2.576 & \text{接受}H_0 \end{array}}$$

• 检验的 p 值 是指在一个假设检验问题中，利用样本观测值能够做出拒绝原假设的最小的显著性水平. 以上例子中，$p=P\{u\leq -2.25\}=\Phi(-2.25)=0.0122$.

---

p 值与检验的显著性

• $p$ 值最初由 R. A. Fisher 提出和使用，常常用来判定假设检验的结果.
• $p$ 值也可以理解为：当原假设为真时，比所得到的样本观察结果更极端的结果出现的概率
  
  • 上例中，$u_p=-2.25$，也即 $p=P\{u\leq -2.25\}$.
• 如果 $p$ 值很小，说明在原假设成立的前提下，样本对应的情况发生的概率很小，这是应该考虑拒绝原假设.
• $p$ 值越小，拒绝原假设的理由越充分，或者说，结果越显著

---

置信区间与假设检验的关系

• 设 $X_1,...,X_n$ 是来自总体 $X$ 的样本，$\Theta$ 是总体参数 $\theta$ 的取值范围.
• 设 $\bbox[lightgreen]{(\underline{\theta}(X_1,...,X_n),\overline{\theta}(X_1,...,X_n))}$ 是参数 $\theta$ 的一个置信水平为 $1-\alpha$ 的置信区间. 也即：对任意 $\theta\in\Theta$，有 $P_{\theta}\left\{ \underline{\theta}(X_1,...,X_n)<\theta<\overline{\theta}(X_1,...,X_n) \right\}\geq 1-\alpha$
• 考虑显著性为 $\alpha$ 的双边检验：$\bbox[yellow]{H_0:\theta=\theta_0,\;H_1:\theta\ne\theta_0.}$
• 注意到 $P_{\theta_0}\left\{ \underline{\theta}(X_1,...,X_n)<\theta_0<\overline{\theta}(X_1,...,X_n) \right\}\geq 1-\alpha.$
• 故拒绝域可以取为 $W_1:\theta_0\notin\bbox[lightgreen]{(\underline{\theta}(x_1,...,x_n),\overline{\theta}(x_1,...,x_n))}.$

---

利用置信区间进行假设检验

对于显著性为 $\alpha$ 的双边检验：

$$H_0:\theta=\theta_0,\quad H_1:\theta\ne\theta_0.$$

1. 先求出 $\theta$ 的置信水平为 $1-\alpha$ 的置信区间 $(\underline{\theta},\overline{\theta})$.

2. 判断 $\theta_0$ 是否落在 $(\underline{\theta},\overline{\theta})$ 中.若 $\theta_0\in(\underline{\theta},\overline{\theta})$，则接受 $H_0$. 反之，拒绝 $H_0$.

   • 类似地，可以通过求以上假设检验问题的拒绝域来求得 $\theta$ 的 $1-\alpha$ 置信区间.

---

7.1.2 正态参数总体假设检验

---

假设检验问题的进一步讨论

回顾：设总体 $X\sim N(\mu,\sigma^2)$，其中 $\sigma^2$ 已知，检验假设

$$H_0:\mu=\mu_0,\quad H_1:\mu\ne\mu_0.$$

• 拒绝域：$\bbox[yellow]{W_1=\left\{(x_1,x_2,...,x_n)\bigg||\overline{x}-\mu_0|>u_{1-\frac{\alpha}{2}}\dfrac{\sigma}{\sqrt{n}}\right\}.}$
• $H_0$ 成立时，检验统计量 $\bbox[yellow]{U=\dfrac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\sim N(0,1).}$

---

进一步的讨论

设总体 $X\sim N(\mu,\sigma^2)$，其中 $\sigma^2$ 已知，检验假设

$$H_0:\mu=\mu_0,\quad \bbox[lightgreen]{H'_1:\mu<\mu_0.}$$

• 拒绝域：$\bbox[lightgreen]{W'_1=\left\{(x_1,x_2,...,x_n)\bigg|\;\overline{x}-\mu_0<u_{\alpha}\dfrac{\sigma}{\sqrt{n}}\right\}.}$
• $H_0$ 成立时，检验统计量 $\bbox[yellow]{U=\dfrac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\sim N(0,1).}$

---

再进一步

设总体 $X\sim N(\mu,\sigma^2)$，其中 $\sigma^2$ 已知，检验假设

$$\bbox[lightblue]{H'_0:\mu\geq\mu_0,}\quad \bbox[lightgreen]{H'_1:\mu<\mu_0.}$$

• 拒绝域：$\bbox[lightgreen]{W'_1=\left\{(x_1,x_2,...,x_n)\bigg|\;\overline{x}-\mu_0<u_{\alpha}\dfrac{\sigma}{\sqrt{n}}\right\}.}$
• $H_0$ 成立时，检验统计量 $\require{enclose}\bbox[yellow]{U=\dfrac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\sim \enclose{horizontalstrike}{N(0,1).}}$

---

为什么使用相同的检验统计量？

$${H'_0:\mu\geq\mu_0,}\quad {H'_1:\mu<\mu_0.}$$

• 由 $\mu\geq\mu_0$ 可得 $U=\dfrac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\geq U'=\dfrac{\overline{X}-\mu}{\sigma/\sqrt{n}}$.
• 进而可得对任意 $C$，总有 $P\{U<C\}\leq P\{U'<C\}$.
• 因为 $U'\sim N(0,1)$，故取 $C=u_{\alpha}$ 即可满足 $P\{U'<C\}\leq\alpha$.
• 进而 $P\{U<u_{\alpha}\}\leq P\{U'<u_{\alpha}\}\leq \alpha$.

---

小结

1. 对于同样的备择假设（$H'_1:\mu<\mu_0$），无论原假设是什么（$H_0:\mu=\mu_0$，$H'_0:\mu\geq\mu_0$），都有相同的拒绝域.

2. 当原假设不是简单假设时，使用的检验统计量与简单假设时相同.

   • 使用简单假设时 $U=\dfrac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\sim N(0,1).$

   • 使用非简单假设时 $\require{enclose}U\sim \enclose{horizontalstrike}{N(0,1).}$

   • 对于任意的假设检验问题，总可以把原假设视为简单假设来处理.

---

单正态总体均值的检验（方差未知）

设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim N(\mu,\sigma^2)$ 的简单随机样本，$\mu,\sigma^2$ 均未知，在显著水平 $\alpha$ 下，检验假设

$$H_0:\;\mu=\mu_0;\quad H_1:\; \mu\ne\mu_0.$$

• 检验统计量： $T=\dfrac{\overline{X}-\mu_{0}}{S / \sqrt{n-1}}=\dfrac{\overline{X}-\mu_{0}}{\tilde{S} / \sqrt{n}}\stackrel{\mu=\mu_0}{\sim}t(n-1)$.
• 拒绝域： $W_1=\left\{(x_1,x_2,...,x_n)\bigg||t|=\dfrac{\left|\overline{x}-\mu_{0}\right|}{s / \sqrt{n-1}}>t_{1-\alpha / 2}(n-1)\right\}$.

---

单正态总体均值的单边检验（方差未知）

设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim N(\mu,\sigma^2)$ 的简单随机样本，$\mu,\sigma^2$ 均未知，$\mu_0$ 已知，在显著水平 $\alpha$ 下，检验假设

$$H_0:\;\mu\leq\mu_0;\quad H_1:\; \mu>\mu_0.$$

• 检验统计量： $T=\dfrac{\overline{X}-\mu_{0}}{S / \sqrt{n-1}}=\dfrac{\overline{X}-\mu_{0}}{\tilde{S} / \sqrt{n}}\stackrel{\mu=\mu_0}{\sim}t(n-1)$.
• 拒绝域： $W_1=\left\{(x_1,x_2,...,x_n)\bigg|t=\dfrac{\overline{x}-\mu_{0}}{s / \sqrt{n-1}}>t_{1-\alpha}(n-1)\right\}$.

---

单正态总体均值的检验：检验统计量与拒绝域

$$\boxed{\begin{array}{c|c|c} H_0 \quad\text{vs}\quad H_1 & \sigma^2\text{ 已知} & \sigma^2\text{ 未知}\\[1em] \hline \text{检验统计量及其分布}& \displaystyle U=\frac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\stackrel{\mu=\mu_0}{\sim} N(0,1) & \displaystyle T=\frac{\overline{X}-\mu_0}{\tilde{S}/\sqrt{n}}\stackrel{\mu=\mu_0}{\sim} t(n-1)\\[1em] \hline \mu=\mu_0,\quad \mu\ne\mu_0 & |u|>u_{1-\frac{\alpha}{2}} & |t|>t_{1-\frac{\alpha}{2}}(n-1)\\[1em] \hline \mu\leq\mu_0,\quad \mu>\mu_0 & u>u_{1-\alpha} & t>t_{1-\alpha}(n-1)\\[1em] \hline \mu\geq\mu_0,\quad \mu<\mu_0 & u<u_{\alpha} & t<t_{\alpha}(n-1) \end{array}}$$

---

例：污水处理问题

某地环保部门规定，废水处理后其中某有毒物质的平均浓度不得超过 $10$ mg/l. 现从某废水处理厂随机抽取了 $15$ 份样本，测得样本均值 $\overline{x}=9.5$ mg/l ，样本标准差 $s=2.5$ mg/l . 假设废水处理后有毒物质的浓度服从正态分布. 试在显著性水平 $0.05$ 下，分析该厂处理后的水是否达标？

---

解

• 由已知，废水处理后有毒物质的浓度 $X\sim N(\mu,\sigma^2)$.
• 检验假设: $H_0:\;\mu\geq10,\quad H_1:\; \mu<\mu_0.$
• 检验统计量：$T=\dfrac{\overline{X}-\mu_{0}}{S / \sqrt{n-1}}$.
• 拒绝域为：$T=\dfrac{\overline{X}-\mu_{0}}{S / \sqrt{n-1}}<-t_{0.95}(14)=-1.761$.
• 查表计算得到 $t=\dfrac{9.5-10}{2.5 / \sqrt{14}}=-0.7483>-1.7613$.
• 接受原假设，认为该废水处理厂处理的废水没有达标.

---

单正态总体方差的检验：检验统计量与拒绝域

$$\boxed{\begin{array}{c|c|c} H_0 \quad\text{vs}\quad H_1 & \mu\text{ 已知} & \mu\text{ 未知}\\[1em] \hline \text{检验统计量及其分布}& \displaystyle \chi^2=\sum\limits_{i=1}^n\left(\frac{X_i-\mu}{\sigma_0}\right)^2\stackrel{\sigma^2=\sigma_0^2}{\sim}\chi^2(n) & \displaystyle \chi^2=\sum\limits_{i=1}^n\left(\frac{X_i-\overline{X}}{\sigma_0}\right)^2\stackrel{\sigma^2=\sigma_0^2}{\sim}\chi^2(n-1)\\[1em] \hline \sigma^2=\sigma^2_0,\quad \sigma^2\ne\sigma^2_0 & \chi^2\notin\left(\chi^2_{\frac{\alpha}{2}}(n),\chi^2_{1-\frac{\alpha}{2}}(n)\right) & \chi^2\notin\left(\chi^2_{\frac{\alpha}{2}}(n-1),\chi^2_{1-\frac{\alpha}{2}}(n-1)\right)\\[1em] \hline \sigma^2\leq\sigma^2_0,\quad \sigma^2>\sigma^2_0 & \chi^2>\chi^2_{1-\alpha}(n) & \chi^2>\chi^2_{1-\alpha}(n-1)\\[1em] \hline \sigma^2\geq\sigma^2_0,\quad \sigma^2<\sigma^2_0 & \chi^2<\chi^2_{\alpha}(n) & \chi^2<\chi^2_{\alpha}(n-1) \end{array}}$$

---

例：产品质量检验

某切割机若正常工作，切割出的金属棒平均长度为 $10$ cm, 标准差不超过 $0.25$ cm. 现从一批产品中随机抽取 $15$ 段，测量得到数据如下:

$$9.9, 10.1, 9.8, 9.9, 10, 9.8, 9.8, 9.9,10.1, 10.1, 10, 10, 9.9, 10, 10.1$$

假设金属棒的长度 $X$ 服从正态分布. 在显著性水平 $\alpha=0.01$ 下，问该切割机是否工作正常？

---

解

• 记切割的金属棒的长度 $X\sim N(\mu,\sigma^2)$，以下分别对 $\sigma^2$ 和 $\mu$ 进行检验.
• 检验假设： ${H}_{0}:\; \sigma \geq {0 . 2 5}, \quad {H}_{1}:\; \sigma<{0 . 2 5}.$
• 检验统计量： $\chi^{2}=15 S^{2} / (0.25)^{2}$.
• 拒绝域：$15 S^{2} / (0.25)^{2}<\chi_{0.01}^{2}(14)$.
• 计算得到：$\dfrac{n S^{2}}{(0.25)^{2}}=\dfrac{15 \times 0.0117333}{0.0625}=2.816<\chi_{0.01}^{2}(14)=4.660$.
• 拒绝原假设，即认为金属棒的加工精度达到了要求.

---

• 检验假设：$H_0:\;\mu=10,\quad H_1:\;\mu\ne10$.
• 检验统计量：$T=\dfrac{\overline{X}-10}{S / \sqrt{14}}$.
• 拒绝域：$|T|=\dfrac{\left|\overline{X}-10\right|}{S / \sqrt{14}}>t_{0.995}(14)$.
• 计算得到：$|t|=1.382<t_{0.995}(14)=2.9763$.
• 接受原假设，即认为切割的金属棒长度的平均长度是 $10$ cm.
• 综上，金属棒的长度均值和方差都符合要求，故认为切割机工作正常.

---

双正态总体均值差的假设检验

设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim N(\mu_1,\sigma^2)$ 的简单随机样本, $Y_1, Y_2, ..., Y_m$ 是来自总体 $Y\sim N(\mu_2,\sigma^2)$ 的简单随机样本, 其中 $\mu_1,\mu_2,\sigma^2$ 均未知，在显著水平 $\alpha$ 下，检验假设

$$H_0:\;\mu_1=\mu_2,\quad H_1:\;\mu_1\ne\mu_2.$$

• 检验统计量 $T=\dfrac{\overline{X}-\overline{Y}}{S_{\omega} \sqrt{1 / n+1 / m}}\sim t(n+m-2).$
  
  • 其中 $S_{\omega}^{2}=\dfrac{n S_{1}^{2}+m S_{2}^{2}}{m+n-2}$, $S_1,S_2$ 分别为 $X_1, X_2, ..., X_n$ 和 $Y_1, Y_2, ..., Y_m$ 的样本方差.

---

双正态总体均值差的检验：检验统计量与拒绝域

$$\boxed{\begin{array}{c|c|c} H_0\quad\text{vs}\quad H_1 & \sigma_1^2,\sigma_2^2\text{ 已知} & \sigma_1^2=\sigma_2^2=\sigma^2\text{ 但未知}\\[1em] \hline \text{检验统计量及其分布} & U=\displaystyle \frac{(\overline{X}-\overline{Y})-\delta}{\sqrt{\dfrac{\sigma_1^2}{m}+\dfrac{\sigma_2^2}{n}}}\stackrel{\mu_1-\mu_2=\delta}{\sim} N(0,1) & T=\displaystyle \frac{(\overline{X}-\overline{Y})-\delta}{S_{\omega}\sqrt{\dfrac{1}{m}+\dfrac{1}{n}}}\stackrel{\mu_1-\mu_2=\delta}{\sim} t(m+n-2)\\[1em] && S^2_{\omega}=\displaystyle\frac{1}{m+n-2}\left[\sum\limits_{i=1}^m(X_i-\overline{X})^2+\sum\limits_{j=1}^n(Y_j-\overline{Y})^2\right]\\ \hline \mu_1-\mu_2=\delta,\quad \mu_1-\mu_2\ne\delta & |u|>u_{1-\frac{\alpha}{2}} & |t|>t_{1-\frac{\alpha}{2}}(m+n-2)\\[1em] \hline \mu_1-\mu_2\le\delta,\quad \mu_1-\mu_2>\delta & u>u_{1-\alpha} & t>t_{1-\alpha}(m+n-2)\\[1em] \hline \mu_1-\mu_2\ge\delta,\quad \mu_1-\mu_2<\delta & u<u_{\alpha} & t<t_{\alpha}(m+n-2)\\[1em] %\hline \end{array}}$$

---

例：NBA 球队胜率比较

右表是马刺队和湖人队历年常规赛成绩，问马刺队的胜率是否明显高于湖人队？($\alpha=0.05$)

$$\begin{array}{c|cc|cc} \hline &\text{马刺队}&&\text{湖人队}&\\ \hline \text{赛季}&\text{胜场}&\text{负场}&\text{胜场}&\text{负场}\\ \hline 2014-2015 & 55 & 27 & 21 & 61\\ 2013-2014 & 62 & 20 & 27 & 55\\ 2012-2013 & 58 & 24 & 45 & 37\\ 2011-2012 & 50 & 16 & 41 & 25\\ 2010-2011 & 61 & 21 & 57 & 25\\ 2009-2010 & 50 & 32 & 57 & 25\\ 2008-2009 & 54 & 28 & 65 & 17\\ 2007-2008 & 56 & 26 & 57 & 25\\ 2006-2007 & 58 & 24 & 42 & 40\\ 2005-2006 & 63 & 19 & 45 & 37\\ 2004-2005 & 59 & 23 & 34 & 48\\ 2003-2004 & 57 & 25 & 56 & 26\\ 2002-2003 & 60 & 22 & 50 & 32\\ 2001-2002 & 58 & 24 & 58 & 24\\ 2000-2001 & 58 & 24 & 56 & 26\\ 1999-2000 & 53 & 29 & 67 & 15\\ 1998-1999 & 53 & 29 & 67 & 15\\ \hline \end{array}$$

---

分析

• 设马刺、湖人两队的常规赛胜率分别为 $X,Y$.
• 设 $X\sim N(\mu_1,\sigma^2),\;Y\sim N(\mu_2,\sigma^2)$.
• 检验假设 $H_0:\;\mu_1\leq\mu_2,\quad H_1:\mu_1>\mu_2$.
• 计算得到
  
  • $\overline{x}=0.700813008,\quad \overline{y}=0.599186992$.
  • $s_{1}^{2}=0.001682861, \quad s_{2}^{2}=0.025041972$.
  • $s_{\omega}^{2}=\frac{n s_{1}^{2}+m s_{2}^{2}}{n+m-2}=0.014316875$.
  • $t=\frac{\overline{x}-\overline{y}}{s_{\omega} \sqrt{1 / n+1 / m}}=2.326>t_{0.95}(28)=1.7011$.
• 拒绝原假设，即认为马刺队的常规赛胜率明显高于湖人队.

---

注： 以上解答过程中存在的问题

1. 二者胜率的方差相等吗？
   
   • 未知！
2. 二者胜率服从正态分布吗？
   
   • 未知！
3. 二者的胜率相互独立吗？
   
   • 未知！

---

例 设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim N(\mu_1,\sigma_1^2)$ 的简单随机样本, $Y_1, Y_2, ..., Y_m$ 是来自总体 $Y\sim N(\mu_2,\sigma_2^2)$ 的简单随机样本, 其中 $\mu_1,\mu_2,$ $\sigma_1^2,\sigma_2^2$ 均未知，在显著水平 $\alpha$ 下，检验假设

$H_0:\;\sigma_1^2=\sigma_2^2,\quad H_0:\;\sigma_1^2\ne\sigma_2^2.$

• 检验统计量 $F=\frac{\tilde{S}_{1}^{2}}{\tilde{S}_{2}^{2}}\sim F(n-1,m-1)$.
• 拒绝域 $F<F_{\frac{\alpha}{2}}(m-1,n-1)$ 或 $F>F_{1-\frac{\alpha}{2}}(m-1,n-1)$.

---

回到前面的例子，比较两队胜率的稳定性

• 记马刺队和湖人队的常规赛胜率分别为 $X,Y$，并作如下假设：
  
  1. $X\sim N(\mu_1,\sigma_1^2),\;Y\sim N(\mu_2,\sigma_2^2)$.
  2. $X,Y$ 相互独立.
• 检验假设：$H_0:\;\sigma_1^2\geq\sigma_2^2,\quad H_1:\sigma_1^2<\sigma_2^2$.
• 计算得到
  
  • $s_{1}^{2}=0.001682861, \quad s_{2}^{2}=0.025041972$,
  • $F=\frac{n s_{1}^{2} /(n-1)}{m s_{2}^{2} /(m-1)}=0.0672<F_{0.05}(14,14)=\frac{1}{F_{0.95}(14,14)}=\frac{1}{2.48}=0.4032$.
• 拒绝原假设，即认为马刺队的常规赛胜率更稳定.

---

双正态总体方差比的检验：检验统计量与拒绝域

$$\boxed{\begin{array}{c|c|c} H_0\quad\text{vs}\quad H_1 & \mu_1,\mu_2\text{已知} & \mu_1,\mu_2\text{均未知}\\[1em] \hline %\text{检验统计量} &\text{及其分布} \text{检验统计量及其分布} & \displaystyle F=\dfrac{\dfrac{1}{m}\sum\limits_{i=1}^m(X_i-\mu_1)^2}{\dfrac{1}{n}\sum\limits_{j=1}^n(Y_j-\mu_2)^2}\stackrel{\sigma_1^2=\sigma_2^2}{\sim} F(m,n) & \displaystyle F=\dfrac{\dfrac{1}{m-1}\sum\limits_{i=1}^m(X_i-\overline{X})^2}{\dfrac{1}{n-1}\sum\limits_{j=1}^n(Y_j-\overline{Y})^2}\stackrel{\sigma_1^2=\sigma_2^2}{\sim} F(m-1,n-1)\\[1em] \hline \sigma_1^2=\sigma_2^2,\quad \sigma_1^2\ne\sigma_2^2 & F\notin\left(F_{\frac{\alpha}{2}}(m,n),F_{1-\frac{\alpha}{2}}(m,n)\right) & F\notin\left(F_{\frac{\alpha}{2}}(m-1,n-1),F_{1-\frac{\alpha}{2}}(m-1,n-1)\right)\\[1em] \hline \sigma_1^2\leq\sigma_2^2,\quad \sigma_1^2>\sigma_2^2 & F>F_{1-\alpha}(m,n) & F>F_{1-\alpha}(m-1,n-1)\\[1em] \hline \sigma_1^2\geq\sigma_2^2,\quad \sigma_1^2<\sigma_2^2 & F<F_{\alpha}(m,n) & F<F_{\alpha}(m-1,n-1)\\[1em] \end{array}}$$

---

7.1.3 非正态总体大样本参数检验

• 在正态总体参数检验中，由于检验统计量都有精确分布，因而对样本大小没有过多限制.
• 对于非正态总体，往往难以找到具有精确分布的检验统计量.
• 当样本容量 $n$ 较大时，可以用检验统计量的渐近分布代替它的精确分布，从而得到近似的拒绝域.
• 中心极限定理: $X_1,X_2,\ldots,X_n$ 独立同分布，总体的期望和方差分别为 $\mu,\sigma^2$，则当 $n$ 较大时， $\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}$ 近似服从 $N(0,1)$.

---

例 某县早稻收割面积为 100 万亩，现随机抽取 150 亩，得到平均亩产量 $\overline{x}=320$ kg，样本的标准差 $s=100$ kg，问在显著性水平 $\alpha=0.05$ 下，能否预计这 100 万亩早稻的平均亩产量为 340 kg?

• 提示：设 $X$ 表示早稻的亩产量.
• 检验假设：${H}_{0}: E(X)=340, \quad {H}_{1} : E(X) \neq 340$.
• 由于 $n=150$ 较大，若 $H_0$ 成立，则近似地有 $\sqrt{n} \frac{\overline{X}-340}{S} \sim N(0 , 1)$.
• 检验的拒绝域为 $\sqrt{150} \frac{|\bar{x}-340|}{s}>u_{1-\alpha / 2}$.

---

例 在两种工艺条件下纺出一批细纱，现随机地各抽取 $100$ 个样品测试其能承受的最大拉力（单位：N）. 经计算得到在这两种工艺条件下样本均值和样本标准差为

• 甲工艺：$\overline{x}=2.80, \quad{s}_1=0.280$
• 乙工艺：$\overline{y}=2.86, \quad{s}_2=0.285$

问在 $\alpha=0.05$ 下，两种工艺条件纺出的细纱的平均强度有无显著差异？

---

解: 设 $X,Y$ 分别表示甲、乙两种工艺条件纺出的细纱总体. 检验假设

$$H_0:E(X)=E(Y),\quad H_1:E(X)\ne E(Y).$$

取统计量 $U=\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{S_{1}^{2}}{m}+\frac{S_{2}^{2}}{n}}}$. 当 $H_0$ 成立时，$U$ 的渐近分布为 $N(0,1)$. 在显著性水平 $\alpha$ 下，拒绝域为 $u>u_{1-\alpha / 2}$.

根据观测值进行计算得到 $u=1.5018<1.96=u_{0.975}$. 因而不能拒绝 $H_0$，即认为在这两种工艺条件下纺出的细纱的平均强力无显著差异.

---

7.1.4 功效函数与最大功效检验

---

例 设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim N(\mu,1)$ 的样本，$\mu$ 未知，在显著水平 $\alpha$ 下，检验假设问题

$H_0:\;\mu=0;\quad H_1:\; \mu\ne0.$

1. 检验1：$W_1:|\overline{x}| >\frac{u_{1-\alpha / 2}}{\sqrt{n}}.$
2. 检验2：$W_1':\overline{x} <\frac{u_{\alpha / 3}}{\sqrt{n}}$ 或 $\overline{x} >\frac{u_{1-2 \alpha / 3}}{\sqrt{n}}.$

3. 检验3：$W_1'':|\overline{x}| >\frac{u_{1-\alpha / 3}}{\sqrt{n}}.$

   • 都满足了 I 类风险要求的情况下，哪一个检验(拒绝域)更好？
   • 或者说，如何量化地比较不同的检验？

---

功效函数

对假设检验问题

$$H_0:\;\theta\in\Theta_0,\quad H_1:\;\theta\in\Theta_1$$

的一个检验 $\phi$ (拒绝域为 $W_1$)，称

$$\beta(\theta)=P\left\{\left(X_{1}, X_{2}, \ldots, X_{n}\right) \in W_1|\theta\right\},\quad (\theta\in\Theta_0\cup\Theta_1)$$

为该检验的 功效函数（势函数, Power Function）.

• 特别地，对 $\theta\in\Theta_1$ 称 $\beta(\theta)$ 为检验 $\phi$ 对于备择假设 $H_1$ 在 $\theta$ 处的 功效 (Power).

---

注： $\boldsymbol{x}=(x_1,x_2,\ldots,x_n)\in W_1\Leftrightarrow$ 拒绝 $H_0$.

1. 若 $\theta\in\Theta_0$，$H_0$ 成立.
   
   • $\beta(\theta)=P\{\boldsymbol{x}\in W_1|\theta\}$ 等于犯第 I 类错误的概率，即 I 类风险.
   • 检验准则一：$\bbox[lightgreen]{\beta(\theta)\leq \alpha}$.
2. 若 $\theta\in\Theta_1$，$H_1$ 成立.
   
   • $\beta(\theta)$ 等于根据样本观测值作出拒绝原假设的判断是正确的概率.
   • $1-\beta(\theta)=P\{\boldsymbol{x}\notin W_1|\theta\}$ 等于犯第 II 类错误的概率，即 II 类风险.
   • 检验准则二：满足 $\beta(\theta)\leq \alpha$ 的同时，使得 $\bbox[yellow]{1-\beta(\theta)}$ 尽可能小（或 $\beta(\theta)$ 尽可能大）.

---

例：功效函数的计算

设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim N(\mu,1)$ 的简单随机样本，其中 $\mu\in(-\infty,+\infty)$ 未知. 在显著水平 $\alpha$ 下，检验假设

$$H_0:\mu=\mu_0,\quad H_1:\mu\ne\mu_0,$$

得到的拒绝域为

$$W_{1}=\left\{\left(x_{1}, x_{2}, \cdots, x_{n}\right)|\sqrt{n}| \overline{x}-\mu_{0} |>u_{1-\alpha / 2}\right\}$$

试求该检验的功效函数 $\beta(\mu)$.

---

解：

• $\beta(\mu)=P_{\mu}\left\{\left(X_{1}, X_{2}, \cdots, X_{n}\right) \in W_{1}\right\}$
  
  • $=P_{\mu}\left\{\sqrt{n}\left|\overline{X}-\mu_{0}\right|>u_{1-\alpha / 2}\right\}$
  • $=P_{\mu}\left\{\sqrt{n}\left(\overline{X}-\mu_{0}\right)<-u_{1-\alpha / 2}\right\}+P_{\mu}\left\{\sqrt{n}\left(\overline{X}-\mu_{0}\right)>u_{1-\alpha / 2}\right\}$
  • $=P_{\mu}\left\{\sqrt{n}\left(\overline{X}-\mu\right)<-u_{1-\alpha / 2}+\sqrt{n}(\mu_0-\mu)\right\}+P_{\mu}\left\{\sqrt{n}\left(\overline{X}-\mu\right)>u_{1-\alpha / 2}+\sqrt{n}(\mu_0-\mu)\right\}$
  • $=\Phi\left(-u_{1-\alpha / 2}+\sqrt{n}(\mu_0-\mu)\right)+\Phi\left(-u_{1-\alpha / 2}-\sqrt{n}(\mu_0-\mu)\right)$
  • $=\Phi\left(u_{\alpha / 2}+\sqrt{n}(\mu_0-\mu)\right)+\Phi\left(u_{\alpha / 2}-\sqrt{n}(\mu_0-\mu)\right)$
• 其中 $\Phi(x)$ 为标准正态分布的分布函数

---

分析： 本例中

$$\beta(\mu)=\Phi\left(u_{\alpha / 2}+\sqrt{n}\left(\mu-\mu_{0}\right)\right)+\Phi\left(u_{\alpha / 2}-\sqrt{n}\left(\mu-\mu_{0}\right)\right)$$

1. $\beta(\mu)$ 的图形关于 $\mu=\mu_0$ 对称.
2. $\mu\ne\mu_0$ 时，$\beta(\mu)>\alpha$.
3. $\beta\left(\mu_{0}\right)=\alpha$ 是 $\beta(\mu)$ 的最小值.

---

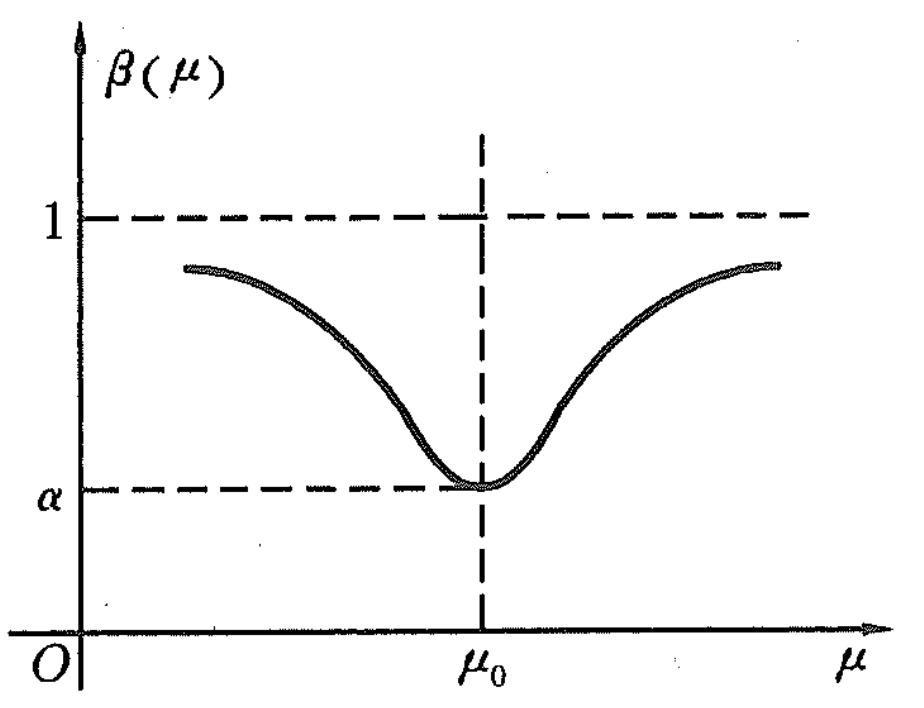
II 类风险的控制

• 本例中，若固定样本容量 $n$，
  
  1. $\mu$ 离 $\mu_0$ 越远，$\beta(\mu)$ 越接近 $1$，检验效果越好.
  2. 若 $\mu\approx\mu_0$，则 $1-\beta(\mu)\approx1-\alpha$.
• 这意味着无法同时使两类风险都很小！
• 一般来说，在 I 类风险可控的前提下，可以通过增加样本容量来降低 II 类风险.

---

增大样本容量以降低 II 类风险

本例中，若已知 $|\mu-\mu_0|\geqslant\delta>0$ ，对于给定的 $\beta\in(0,1)$，要使 II 类风险不超过 $\beta$，$n$ 应该取多大？

• 分析：当 $n$ 较大时，$\Phi\left(u_{a / 2}-\sqrt{n}|\mu-\mu_0|\right) \approx 0$.
• 只需 $\Phi\left(u_{a / 2}+\sqrt{n}|\mu-\mu_0|\right)\geq \Phi\left(u_{a / 2}+\sqrt{n} \delta\right)\geq 1-\beta$，即可满足对 II 类风险的要求.
• 上式后一部分也即 $\Phi\left(-u_{a / 2}-\sqrt{n} \delta\right)\leq \beta$.
• 由此最终可解得 $n \geqslant\left(\frac{u_{1-\alpha / 2}-u_{\beta}}{\delta}\right)^{2}$.

---

例：单边检验的功效函数

设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim N(\mu,\sigma_0^2)$ 的简单随机样本，其中 $\sigma_0^2$ 已知，$\mu$ 未知. 在显著水平 $\alpha$ 下，检验假设

$$H_0:\mu\leq\mu_0,\quad H_1:\mu>\mu_0.$$

采用 $u$ 检验，试求该检验的功效函数 $\beta(\mu)$.

---

分析

• 检验的拒绝域 $\frac{\overline{X}-\mu_{0}}{\sigma_{0} / \sqrt{n}}>u_{1-\alpha}$.
• $\beta(\mu)=P_{\mu}\left\{\frac{\overline{X}-\mu_{0}}{\sigma_{0} / \sqrt{n}}>u_{1-\alpha}\right\}$
  
  • $=P_{\mu}\left\{\frac{\overline{X}-\mu}{\sigma_{0} / \sqrt{n}}>u_{1-\alpha}+\frac{\mu_{0}-\mu}{\sigma_{0} / \sqrt{n}}\right\}$
  • $=1-P_{\mu}\left\{\frac{\overline{X}-\mu}{\sigma_{0} / \sqrt{n}} \leq u_{1-\alpha}+\frac{\mu_{0}-\mu}{\sigma_{0} / \sqrt{n}}\right\}$
  • $=1-\Phi\left(u_{1-\alpha}+\frac{\mu_{0}-\mu}{\sigma_{0} / \sqrt{n}}\right)$.
• $\beta(\mu)$ 关于 $\mu$ 单调增加.

---

• II 类风险: $1-\beta(\mu)=\Phi\left(u_{1-\alpha}+\frac{\mu_{0}-\mu}{\sigma_{0} / \sqrt{n}}\right).$
• 设 $\mu_0=0,\sigma_0=1,\alpha=0.05$，要使 $\mu\geq1$ 时，该检验的 II 类风险不大于 $0.10$，则令
  
  • $\Phi\left(u_{0.95}-\sqrt{n}(1-0)\right) \leqslant 0.1$
  • $\Rightarrow\sqrt{n} \geqslant u_{0.95}+u_{0.90}$.
  • $\Rightarrow n\geqslant 8.57$.
• 结论：样本容量至少为 $9$ 才能使这个检验的 II 类风险不大于 $0.10$.

---

例：工厂产品质量抽验方案

• 设有一大批产品，产品质量指标 $X\sim N(\mu,\sigma^2)$，以 $\mu$ 小者为佳.
• 厂方要求所确定的验收方案对高质量的产品 $(\mu\leq\mu_0)$ 能以高于概率 $1-\alpha$ 为买方所接受.
• 买方则要求低质产品 $(\mu\geq\mu_0+\delta,\;\delta>0)$ 能以高于概率 $1-\beta$ 被拒绝.
• $\alpha,\beta$ 由厂方与买方协商给出，并采取一次抽样以确定该批产品是否为买方所接受.
• 已知 $\mu_0=120,\delta=20$, 且由工厂长期经验知 $\sigma^2=900$. 又经商定 $\alpha,\beta$ 均取为 $0.05$.
• 应该怎样安排抽样方案？

---

提示：

• 考虑显著性水平为 $\alpha$ 的检验问题：$H_0:\mu\leq\mu_0,\;H_1:\mu>\mu_0$.
• 且要求当 $\mu\geq\mu_0+\delta$ 时 II 类风险不超过 $1-\beta(\mu)\leq\beta$.
• 拒绝域 $W_1:\frac{\overline{x}-\mu_0}{\sigma/\sqrt{n}}\geq u_{1-\alpha}$.
• $\beta(\mu)=P_{\mu}\left\{ \frac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\geq u_{1-\alpha} \right\}$
• $=P_{\mu}\left\{ \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\geq u_{1-\alpha}-\frac{\mu-\mu_0}{\sigma/\sqrt{n}} \right\}=\Phi\left(\frac{\mu-\mu_0}{\sigma/\sqrt{n}}-u_{1-\alpha} \right).$

---

• $\beta(\mu)=\Phi\left(\frac{\mu-\mu_0}{\sigma/\sqrt{n}}-u_{1-\alpha} \right).$
• 现要求当 $\mu\geq\mu_0+\delta$ 时 $1-\beta(\mu)\leq \beta$.
• 也即 $\beta(\mu)\geq 1-\beta$，由此解得 $n\geq\left[ \frac{(u_{1-\alpha}+u_{1-\beta})\sigma}{\delta} \right]^2.$
• 代入数据计算得 $n\geq 24.35$.
• 结论： 取 $n=25$，当 $\frac{\overline{x}-120}{30/\sqrt{5}}\geq u_{0.05}$，也即 $\overline{x}\geq 129.87$ 时，买方就拒绝这批产品；否则，若 $\overline{x}<129.87$，则买方应接受这批产品.

---

N-P准则

• 对于同一个假设检验问题，在相同的显著性水平 $\alpha$ 下可以给出不同的检验，这些检验的功效函数是不同的.
• 1930s, Neyman- Pearson（N-P准则）：在 I 类风险满足显著性水平 $\alpha$ 的前提下，使 II 类风险尽可能小，即要求这个检验的功效函数 $\beta(\theta)$ 满足：
  
  • $\left\{\begin{array}{l}\beta(\theta)\leqslant\alpha,& \theta\in\Theta_0\\ \beta(\theta)\text{尽可能大}, & \theta\in\Theta_1\end{array}\right.$

---

最大功效检验（MPT）

对显著水平为 $\alpha$ 的假设检验问题

$$H_0:\theta\in\Theta_0,\quad H_1:\theta\in\Theta_1.$$

如果检验 $\phi^*$，使得对于任意一个检验 $\phi$，均有

$$\beta_{\phi^*}(\theta)\geqslant\beta_{\phi}(\theta),\quad (\theta\in\Theta_1)$$

则称 $\phi^*$ 为这个假设检验问题在显著性水平 $\alpha$ 下的 一致最大功效检验（UMPT, Uniformly Most Powerful Test）. 当 $H_1$ 为简单假设时，称为 最大功效检验（MPT）

---

Neyman-Pearson 引理

设总体 $X$ 的概率密度为 $f(x; \theta)$, 对显著水平为 $\alpha$ 的假设检验问题 $H_0:\theta=\theta_0, H_1:\theta=\theta_1$, 如果存在临界值 $k$, 使

$$P_{\theta_{0}}\left\{\frac{\prod_{i=1}^{n} f\left(X_{i} ; \theta_{1}\right)}{\prod_{i=1}^{n} f\left(X_{i} ; \theta_{0}\right)}>k\right\}=\alpha$$

那么，以

$$W_{1}^{*}=\left\{\left(x_{1}, x_{2}, \cdots, x_{n}\right) \Bigg| \frac{\prod_{i=1}^{n} f\left(x_{i} ; \theta_{1}\right)}{\prod_{i=1}^{n} f\left(x_{i} ; \theta_{0}\right)}>k\right\}$$

为拒绝域的检验 $\phi^*$ 是该假设检验问题的 MPT.

---

似然比

$$l\left(\boldsymbol{x}\right)=\frac{\prod_{i=1}^{n} f\left(x_{i} ; \theta_{1}\right)}{\prod_{i=1}^{n} f\left(x_{i} ; \theta_{0}\right)}=\frac{L(\theta_1;\boldsymbol{x})}{L(\theta_0;\boldsymbol{x})},\quad \boldsymbol{x}=(x_1,x_2,...,x_n).$$

• 称为 似然比 (Likelihood Ratio)，也即似然函数 $L(\theta;\boldsymbol{x})$ 在 $\theta_1,\theta_0$ 处的取值之比.
• Neyman-Pearson 引理给出的检验也称为 似然比检验.
• 似然函数 $L(\theta;\boldsymbol{x})$ 刻画了样本落在 $(x_1,x_2,\ldots,x_n)$ 附近的可能性的大小.
  
  • $H_0$ 成立时，$l\left(\boldsymbol{x}\right)$ 应该较小；反之，$l\left(\boldsymbol{x}\right)$ 则应该较大.

---

证明：

• 设 $W_1$ 为任一其他检验的拒绝域，于是 $P(W_1|\theta_0)\leq\alpha= P(W_1^*|\theta_0)$.
• $P(W_1^*|\theta)=P(W_1^* W_1|\theta)+P(W_1^*-W_1|\theta)$；
• $P(W_1|\theta)=P(W_1^* W_1|\theta)+P(W_1-W_1^*|\theta)$，
• 由此即知 $P(W_1^*-W_1|\theta_0)\geq P(W_1-W_1^*|\theta_0)$.
• 两个检验的功效分别为 $P(W_1^*|\theta_1)$ 和 $P(W_1|\theta_1)$，
• 以下证明 $P(W_1^*|\theta_1)\geq P(W_1|\theta_1)$.

---

• 要证明 $P(W_1^*|\theta_1)\geq P(W_1|\theta_1)$，只须证明 $P(W_1^*-W_1|\theta_1)\geq P(W_1-W_1^*|\theta_1)$.
• $\displaystyle P(W_1^*-{W_1}|\theta_1)=\int_{W_1^*-{W_1}}L(\theta_1;\boldsymbol{x})\mathrm{d}\boldsymbol{x}$
  
  • $\displaystyle \geq k\int_{W_1^*-{W_1}}L(\theta_0;\boldsymbol{x})\mathrm{d}\boldsymbol{x}=kP(W_1^*-{W_1}|\theta_0)$
  • $\displaystyle \geq kP(W_1-W_1^*|\theta_0)=k\int_{W_1-W_1^*}L(\theta_0;\boldsymbol{x})\mathrm{d}\boldsymbol{x}$
  • $\displaystyle >\int_{W_1-W_1^*}L(\theta_1;\boldsymbol{x})\mathrm{d}\boldsymbol{x}=P(W_1-W_1^*|\theta_1)$.

---

例：求最大功效检验

设 $X_1, X_2, \ldots, X_n$ 是取自总体 $X\sim N (\mu;1)$ 的简单随机样本，其中 $\mu$ 未知，要检验

$$H_0:\mu=\mu_0,\quad H_1:\mu=\mu_1.$$

其中 $\mu_0<\mu_1$，在显著性水平 $\alpha$ 下，求最大功效检验的拒绝域.

---

解：

• $\prod_{i=1}^{n} f\left(x_{i} ; \mu\right)=(2 \pi)^{-\frac{n}{2}} \exp \left[-\frac{1}{2} \sum_{i=1}^{n}\left(x_{i}-\mu\right)^{2}\right].$
• $l\left(x_{1}, x_{2}, \cdots, x_{n}\right)=\exp \left[n\left(\mu_{1}-\mu_{0}\right) \overline{x}-\frac{n}{2}\left(\mu_{1}^{2}-\mu_{0}^{2}\right)\right].$
• 由 Neyman-Pearson 定理，MPT 的拒绝域形如
  
  • $W_{1}^{*}=\left\{\left(x_{1}, x_{2}, \cdots, x_{n}\right) | l\left(x_{1}, x_{2}, \cdots, x_{n}\right)>k\right\}$
    
    • $=\left\{\left(x_{1}, x_{2}, \cdots, x_{n}\right) | \overline{x}>k_{1}\right\}$
    • $=\left\{\left(x_{1}, x_{2}, \cdots, x_{n}\right) | \sqrt{n}\left(\overline{x}-\mu_{0}\right)>k_{0}\right\}.$
  • 其中 $k_{1}=\left[\ln k+\frac{n}{2}\left(\mu_{1}^{2}-\mu_{0}^{2}\right)\right] / n\left(\mu_{1}-\mu_{0}\right)$，$k_{0}=\sqrt{n}\left(k_{1}-\mu_{0}\right)$.

---

• $H_0$ 成立时，$\sqrt{n}\left(\overline{X}-\mu_{0}\right) \sim N(0 ; 1)$.
• 取临界值 $k_0=u_{1-\alpha}$，则 $P_{\mu_{0}}\left\{\sqrt{n}\left(\overline{X}-\mu_{0}\right)>u_{1-a}\right\}=\alpha$.
• 故所求 MPT 的拒绝域为 $W_{1}^{*}=\left\{\left(x_{1}, x_{2}, \cdots, x_{n}\right) | \sqrt{n}\left(\overline{x}-\mu_{0}\right)>u_{1-\alpha}\right\}.$

---

例：求一致最大功效检验

设 $X_1, X_2,\ldots, X_n$ 是取自 $X\sim N (\mu;1)$ 的样本，其中 $\mu$ 未知，证明对于单侧假设检验问题

$H_0:\mu\leqslant\mu_0,\quad H_1:\mu>\mu_0.$

前例给出的拒绝域为

$$W_{1}^{*}=\left\{\left(x_{1}, x_{2}, \cdots, x_{n}\right) | \sqrt{n}\left(\overline{x}-\mu_{0}\right)>u_{1-\alpha}\right\}$$

的 $u$-检验 $\phi^*$ 是显著性水平 $\alpha$ 下的一致最大功效检验(UMPT).

---

证明：

• 由前例：任给 $\mu_1>\mu_0$, 对检验 $H'_0:\mu=\mu_0,\;H'_1:\mu=\mu_1$，$\phi^*$ 是显著性水平 $\alpha$ 下的最大功效检验.
• 由于 $W_1^*$ 与 $\mu_1$ 的取值无关，所以对于检验 $H'_0:\mu=\mu_0,\;\bbox[lightgreen]{H''_1:\mu>\mu_0}$，$\phi^*$ 是显著性水平 $\alpha$ 下的一致最大功效检验.
• 设 $\phi$ 是原假设问题 $H_0:\mu\leqslant\mu_0,\; H_1:\mu>\mu_0$ 的显著性水平 $\alpha$ 下的任意一个检验，拒绝域为 $W_1$.
  
  • 当 $H_0:\mu\leqslant\mu_0$ 成立时，$P_{\mu}\left\{\left(X_{1}, X_{2}, \cdots, X_{n}\right) \in W_{1}\right\} \leqslant \alpha$.
  • 显然 $\phi$ 也是假设检验问题 $H'_0\;\mathrm vs\; H''_1$ 的一个显著性水平 $\alpha$ 的检验.

---

• $\phi^*$ 是检验问题 $H'_0\;\mathrm vs\; H''_1$ 的一致最大功效检验，故当$\mu>\mu_0$ 时，必有 $\beta_{\phi^*}(\mu) \geqslant \beta_{\phi}(\mu)$.
• 可以验证 $\phi^*$ 是原假设问题的一个显著性水平 $\alpha$ 下的检验.
• 因此，$\phi^*$ 也是原假设检验问题的一直最大功效检验.

---

小结

• 参数假设检验
  
  • 问题的提法
  • 统计量的选择
  • 结果的理解
• 正态总体参数的假设检验
  
  • 单正态总体
  • 双正态总体