1.3 内积空间

高等工程数学 讲义 2024AU

---

---

1.3.1 内积的定义与性质

设 $V$ 是实线性空间，若对任意的 $\boldsymbol{\alpha},\boldsymbol{\beta}\in V$ ，都有一个实数与之对应，记该实数为 $\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle$ ，且满足

1. 对称性： $\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle =\langle \boldsymbol{\beta},\boldsymbol{\alpha}\rangle$
2. 可加性： $\langle \boldsymbol{\alpha}+\boldsymbol{\beta},\boldsymbol{\xi}\rangle =\langle \boldsymbol{\alpha},\boldsymbol{\xi}\rangle +\langle \boldsymbol{\beta},\boldsymbol{\xi}\rangle ,\;\boldsymbol{\xi}\in V$
3. 齐次性： $\langle k\boldsymbol{\alpha},\boldsymbol{\beta}\rangle =k\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle ,\;k\in\mathbb{R}$
4. 正定性： $\langle \boldsymbol{\alpha},\boldsymbol{\alpha}\rangle \geq 0$ ，且 $\langle \boldsymbol{\alpha},\boldsymbol{\alpha}\rangle =0\Rightarrow\boldsymbol{\alpha}=0$

则称 $\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle$ 为 $\boldsymbol{\alpha}$ 与 $\boldsymbol{\beta}$ 的 内积 (Inner Product)

• 定义了内积的实线性空间称为 欧氏空间 (Eculidean Space)

---

欧式空间中的内积

例 设 $\boldsymbol{x},\boldsymbol{y}\in\mathbb{R}^n,\;\boldsymbol{A}\in\mathbb{R}^{n\times n}$ ，以下 $\langle \boldsymbol{x},\boldsymbol{y}\rangle$ 是内积吗？

• $\langle \boldsymbol{x}, \boldsymbol{y}\rangle \triangleq \boldsymbol{x}^{\mathrm{T}} \boldsymbol{y}=\boldsymbol{y}^{\mathrm{T}} \boldsymbol{x}=\sum_{i=1}^{n} x_{i} y_{i}$
  
  • 是的.

• $\langle \boldsymbol{x}, \boldsymbol{y}\rangle \triangleq \boldsymbol{x}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{y}=\boldsymbol{y}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{x}=\sum_{i=1}^{n} \sum_{j=1}^{n} x_{i} a_{i j} y_{j}$

  • 不是！除非 $\boldsymbol{A}$ 是正定矩阵！

• 同一个线性空间可以定义不同的内积

---

函数空间上的内积

例 记 $C_{[a,b]}$ 表示定义在 $[a,b]$ 区间上的连续函数全体. 令

$$\langle f, g\rangle \triangleq \int_{a}^{b} f(x) g(x) \mathrm{d} x, \quad \forall f, g \in C_{[a, b]}$$

可验证 $\langle f,g\rangle$ 是内积.

---

酉空间

设 $V$ 是复线性空间，若对任意的 $\boldsymbol{\alpha},\boldsymbol{\beta}\in V$ ，都有一个复数与之对应，记该复数为 $\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle$ ，且满足

1. 共轭对称性： $\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle =\overline{\langle \boldsymbol{\beta},\boldsymbol{\alpha}\rangle }$
2. 可加性： $\langle \boldsymbol{\alpha}+\boldsymbol{\beta},\boldsymbol{\xi}\rangle =\langle \boldsymbol{\alpha},\boldsymbol{\xi}\rangle +\langle \boldsymbol{\beta},\boldsymbol{\xi}\rangle ,\;\boldsymbol{\xi}\in V$
3. 齐次性： $\langle k\boldsymbol{\alpha},\boldsymbol{\beta}\rangle =k\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle ,\;k\in\mathbb{C}$

4. 正定性： $\langle \boldsymbol{\alpha},\boldsymbol{\alpha}\rangle \geq 0$ ，且 $\langle \boldsymbol{\alpha},\boldsymbol{\alpha}\rangle =0\Rightarrow\boldsymbol{\alpha}=0$

   • 则称 $\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle$ 为 $\boldsymbol{\alpha}$ 与 $\boldsymbol{\beta}$ 的 内积
   • 定义了内积的复线性空间称为 酉空间 (Unitary Space)

---

酉空间上的内积

例 对任意 $\boldsymbol{x},\boldsymbol{y}\in\mathbb{C}^n$ ，

$$\langle \boldsymbol{x}, \boldsymbol{y}\rangle \triangleq \boldsymbol{x}^{\mathrm{T}} \overline{\boldsymbol{y}}=\sum_{i=1}^{n} x_{i} \overline{y}_{i}$$

是内积

• 以上的内积也可以写为：$\langle \boldsymbol{x}, \boldsymbol{y}\rangle \triangleq \boldsymbol{y}^{\mathrm{H}} \boldsymbol{x}$

• $\boldsymbol{A}^{\mathrm{H}}=\overline{\boldsymbol{A}^{\mathrm{T}}}$ 表示 $\boldsymbol{A}$ 的 共轭转置 (Conjugate Transpose)

---

酉空间上内积的性质

对 $\forall\boldsymbol{\alpha},\boldsymbol{\beta},\boldsymbol{\alpha}_i,\boldsymbol{\beta}_j\in V(\mathbb{C}),\;\forall k,x_i,y_j\in\mathbb{C}$，

1. $\langle \boldsymbol{\alpha},\boldsymbol{0}\rangle =\langle \boldsymbol{0},\boldsymbol{\alpha}\rangle =0$
2. $\langle \boldsymbol{\alpha},k\boldsymbol{\beta}\rangle =\overline{k}\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle$
3. $\bbox[yellow]{\displaystyle\left\langle \sum_{i=1}^{n} x_{i} \boldsymbol{\alpha}_{i}, \sum_{j=1}^{m} y_{j} \boldsymbol{\beta}_{j}\right\rangle =\sum_{i=1}^{n} \sum_{j=1}^{m} x_{i}\left\langle \boldsymbol{\alpha}_{i}, \boldsymbol{\beta}_{j}\right\rangle \overline{y}_{j}}$
   
   • 记 $\boldsymbol{A}=\left[\left\langle \boldsymbol{\alpha}_{i}, \boldsymbol{\beta}_{j}\right\rangle\right]_{n\times m}$，则上式右端可写为 $\boldsymbol{x}^{\mathrm{T}}\boldsymbol{A}\overline{\boldsymbol{y}}$ 或 $\boldsymbol{y}^{\mathrm{H}}\boldsymbol{A}^{\mathrm{T}}{\boldsymbol{x}}$.

---

向量的长度

设 $V$ 是 $n$ 维内积空间， $\forall\boldsymbol{\alpha}\in V$ ，

$$|\boldsymbol{\alpha}| \triangleq \left({\langle \boldsymbol{\alpha}, \boldsymbol{\alpha}\rangle }\right)^{1/2}$$

称为 $\boldsymbol{\alpha}$ 的 长度

• 单位向量(Unit Vector)：长度为 $1$ 的向量
• 单位化向量(Normalized Vector)： $\boldsymbol{\alpha}^{0} \triangleq \frac{\boldsymbol{\alpha}}{|\boldsymbol{\alpha}|}$ ，其中 $\boldsymbol{\alpha}\ne\boldsymbol{0}$

---

长度的性质

1. 非负性： $|\boldsymbol{\alpha}| \geq {0} ; \quad|\boldsymbol{\alpha}|=0 \Leftrightarrow \boldsymbol{\alpha}=0$
2. 齐次性： $|k\boldsymbol{\alpha}|=|k||\boldsymbol{\alpha}|,\;k\in\mathbb{C}$
3. Cauchy-Schwartz不等式： $|\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle |\leq|\boldsymbol{\alpha}||\boldsymbol{\beta}|$
   
   • 且 $|\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle |=|\boldsymbol{\alpha}||\boldsymbol{\beta}|\Leftrightarrow\boldsymbol{\alpha},\boldsymbol{\beta}$ 线性相关
   • 例：在 $\mathbb{R}^n$ 中， $\left|\sum_{i=1}^{n} x_{i} y_{i}\right| \leq \sqrt{\sum_{i=1}^{n} x_{i}^{2}} \cdot \sqrt{\sum_{i=1}^{n} y_{i}^{2}}$
   • 例：在 $C_{[a,b]}$ 中 $\left|\int_{a}^{b} f(x) g(x) d x\right| \leq \sqrt{\int_{a}^{b} f^{2}(x) d x} \cdot \sqrt{\int_{a}^{b} g^{2}(x) d x}$
4. 三角不等式： $|\boldsymbol{\alpha}+\boldsymbol{\beta}|\leq|\boldsymbol{\alpha}|+|\boldsymbol{\beta}|$

---

Cauchy-Schwartz不等式的证明（欧式空间）

• 对任意 $x\in\mathbb{R}$ ， $\langle x\boldsymbol{\alpha}+\boldsymbol{\beta},x\boldsymbol{\alpha}+\boldsymbol{\beta}\rangle \geq 0$
  
  • 即$|\boldsymbol{\alpha}|^2x^2+2\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle x+|\boldsymbol{\beta}|^2\geq0$
• 由根的判别式，须 $\Delta=(2\langle \boldsymbol{\alpha}, \boldsymbol{\beta}\rangle )^{2}-4|\boldsymbol{\alpha}|^{2}|\boldsymbol{\beta}|^{2} \leq 0$
• 又若 $\boldsymbol{\alpha}=k\boldsymbol{\beta}$ ，显然 $|\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle |=|\boldsymbol{\alpha}||\boldsymbol{\beta}|$
• 若 $|\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle |=|\boldsymbol{\alpha}||\boldsymbol{\beta}|$
  
  • $\boldsymbol{\alpha}=\boldsymbol{0}$ 时，显然 $\boldsymbol{\alpha},\boldsymbol{\beta}$ 线性相关
  • $\boldsymbol{\alpha}\ne\boldsymbol{0}$ 时，令 $x=-\frac{\langle \boldsymbol{\alpha}, \boldsymbol{\beta}\rangle }{|\boldsymbol{\alpha}|^{2}}$ ，则 $\langle x\boldsymbol{\alpha}+\boldsymbol{\beta},x\boldsymbol{\alpha}+\boldsymbol{\beta}\rangle =0$
  • 于是 $x\boldsymbol{\alpha}+\boldsymbol{\beta}=0$ ，即二者线性相关

---

Cauchy-Schwartz不等式的证明（酉空间）

• 对任意 $x\in\mathbb{C}$ ， $\langle x\boldsymbol{\alpha}+\boldsymbol{\beta},x\boldsymbol{\alpha}+\boldsymbol{\beta}\rangle \geq 0$
• 即 $|x|^2|\boldsymbol{\alpha}|^2+2\mathrm{Re}(x\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle )+|\boldsymbol{\beta}|^2\geq0$
  
  • $\mathrm{Re}(x)$ 表示取 $x$ 的实部
• 注意到，对任意 $x,y\in\mathbb{C}$，$\mathrm{Re}(xy)\leq|x||y|$ （请自行验证）
  
  • 故 $\mathrm{Re}(x\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle )\leq|x||\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle |$
• 从而 $|\boldsymbol{\alpha}|^2|x|^2+2|\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle ||x|+|\boldsymbol{\beta}|^2\geq0$
• 上式任意 $x\in\mathbb{C}$成立，须
  
  • $\Delta=4|\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle |-4|\boldsymbol{\alpha}|^2|\boldsymbol{\beta}|^2\leq0$
• 剩余部分的证明参考欧式空间对应的证明即可

---

度量矩阵

设 $\boldsymbol{B}=\{\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\ldots,\boldsymbol{\alpha}_n\}$ 是内积空间 $V^n$ 的基

• 对任意 $\boldsymbol{\alpha}=\boldsymbol{B}\boldsymbol{x},\boldsymbol{\beta}=\boldsymbol{B}\boldsymbol{y}\in V^n$
  
  • 其中 $\boldsymbol{x}=[x_1\;\;x_2\;...\;x_n]^{\mathrm{T}},\boldsymbol{y}=[y_1\;\;y_2\;...\;y_n]^{\mathrm{T}}$
• $\langle\boldsymbol{\alpha},\boldsymbol{\beta}\rangle=\left\langle\sum\limits_{i=1}^nx_i\boldsymbol{\alpha}_i,\sum\limits_{j=1}^ny_j\boldsymbol{\alpha}_j\right\rangle=\sum\limits_{i=1}^n\sum\limits_{j=1}^nx_i\langle\boldsymbol{\alpha}_i,\boldsymbol{\alpha}_j\rangle \overline{y}_j$
• 定义 $\boldsymbol{B}$ 的度量矩阵(Metric Matrix)： $\boldsymbol{G}=[\langle \boldsymbol{\alpha}_i,\boldsymbol{\alpha}_j\rangle ]_{n\times n}$
  
  • 则 $\langle\boldsymbol{\alpha},\boldsymbol{\beta}\rangle=\boldsymbol{x}^{\mathrm{T}}\boldsymbol{G}\overline{\boldsymbol{y}}$
• 对任意非零向量 $\boldsymbol{x}\in \mathbb{C}^n$，$\boldsymbol{x}^{\mathrm{T}}\boldsymbol{G}\overline{\boldsymbol{x}}=\langle \boldsymbol{B}\boldsymbol{x},\boldsymbol{B}\boldsymbol{x}\rangle=|\boldsymbol{B}\boldsymbol{x}|^2> 0$
  
  • 由此可知 $\boldsymbol{G}$ 是正定矩阵

---

欧式空间中的度量矩阵

设 $V^n$ 是欧式空间，$\boldsymbol{B}$ 是 $V^n$ 的基.

• 若定义 $V^n$ 上的内积为 $\langle\boldsymbol{\alpha},\boldsymbol{\beta}\rangle=\boldsymbol{\alpha}^{\mathrm{T}}\boldsymbol{\beta},(\boldsymbol{\alpha},\boldsymbol{\beta}\in V^n)$，则
• $\boldsymbol{G}=\boldsymbol{B}^{\mathrm{T}}\boldsymbol{B}$
• 若 $\boldsymbol{G}=\boldsymbol{I}$
  
  • 对 $\boldsymbol{\alpha}=\boldsymbol{B}\boldsymbol{x},\boldsymbol{\beta}=\boldsymbol{B}\boldsymbol{y}$，$\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle=\boldsymbol{x}^{\mathrm{T}}\boldsymbol{G}\boldsymbol{y}=\boldsymbol{x}^{\mathrm{T}}\boldsymbol{y}$
• $\boldsymbol{G}=\boldsymbol{I}$ 意味着什么？
  
  • 或者说，什么情况下 $\boldsymbol{G}=\boldsymbol{I}$？

---

1.3.2 向量的正交与 Schmidt 正交化

设 $V$ 是内积空间， $\boldsymbol{\alpha},\boldsymbol{\beta}\in V$

• $\boldsymbol{\alpha},\boldsymbol{\beta}$ 正交(Orthogonal)，是指： $\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle =0$
  
  • 记为 $\boldsymbol{\alpha}\perp\boldsymbol{\beta}$
• 勾股定理(Pythagorean Theorem)
  
  • $\boldsymbol{\alpha}\perp\boldsymbol{\beta}\Leftrightarrow|\boldsymbol{\alpha}+\boldsymbol{\beta}|^2=|\boldsymbol{\alpha}|^2+|\boldsymbol{\beta}|^2$

---

例 求 $\mathbb{R}^4$ 中的单位向量 $\boldsymbol{\alpha}$ ，使之与如下向量均正交

$$\boldsymbol{\alpha}_1=\left[\begin{array}{r}1\\1\\-1\\1\end{array}\right],\quad \boldsymbol{\alpha}_2=\left[\begin{array}{r}1\\-1\\-1\\1\end{array}\right],\quad \boldsymbol{\alpha}_3=\left[\begin{array}{r}2\\1\\1\\3\end{array}\right]$$

---

提示

• 设所求向量为 $\boldsymbol{\alpha}=[x_1\;x_2\;x_3\;x_4]^{\mathrm{T}}$
• 则 $\left\{\begin{array}{l}{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}=1} \\ {x_{1}+x_{2}-x_{3}+x_{4}=0} \\ {x_{1}-x_{2}-x_{3}+x_{4}=0} \\ {2 x_{1}+x_{2}+x_{3}+3 x_{4}=0}\end{array}\right.$
• 联立后三个方程，解得基础解系 $[4\;\;0\;\;1\;\;-3]^{\mathrm{T}}$
• 单位化可得 $\boldsymbol{\alpha}=\frac{1}{\sqrt{26}}[4\;\;0\;\;1\;\;-3]^{\mathrm{T}}$

---

正交向量组

设 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\ldots,\boldsymbol{\alpha}_r$ 是 $n$ 维内积空间 $V^n$ 中的非零向量，若其中的向量两两正交，则称其为 正交向量组.

• $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\ldots,\boldsymbol{\alpha}_r$ 是正交向量组 $\Rightarrow \boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\ldots,\boldsymbol{\alpha}_r$ 线性无关.
• $V^n$ 中的正交向量组 $\boldsymbol{B}=\{\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\ldots,\boldsymbol{\alpha}_n\}$ 称为 $V^n$ 的 正交基.
  
  • 若以上 $\boldsymbol{B}$ 中的向量均为单位向量，则称 $\boldsymbol{B}$ 为 $V^n$ 的 标准正交基 (Normal Orthogonal Basis)

---

标准正交基的判定

定理 以下条件等价：

1. $\boldsymbol{B}=\{\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\ldots,\boldsymbol{\alpha}_n\}$是 $V^n$ 的标准正交基
2. $\langle \boldsymbol{\alpha}_{i}, \boldsymbol{\alpha}_{j}\rangle =\delta_{i j}=\left\{\begin{array}{ll}{1,} & {i=j} \\ {0,} & {i \neq j}\end{array} \;i,j=1,2, \cdots, n\right.$
3. $\boldsymbol{B}$ 的度量矩阵是单位阵
4. $\forall\boldsymbol{\beta}\in V^n$ ， $\displaystyle\boldsymbol{\beta}=\sum_{i=1}^{n}\langle \boldsymbol{\beta}, \boldsymbol{\alpha}_{i}\rangle \boldsymbol{\alpha}_{i}$
   
   • 或 $\boldsymbol{\beta}=\boldsymbol{B}\;\left[\langle \boldsymbol{\beta}, \boldsymbol{\alpha}_{1}\rangle\;\;\langle \boldsymbol{\beta}, \boldsymbol{\alpha}_{2}\rangle ... \langle \boldsymbol{\beta}, \boldsymbol{\alpha}_{n}\rangle\right]^{\mathrm{T}}$

---

Schmidt 正交化

设 $\{\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\ldots,\boldsymbol{\alpha}_n\}$ 是 $n$ 维内积空间 $V^n$ 的基，利用如下的方法可以得到 $V^n$ 的一组标准正交基 $\{\boldsymbol{\varepsilon}_1,\boldsymbol{\varepsilon}_2,\ldots,\boldsymbol{\varepsilon}_n\}$

1. 令 $\boldsymbol{\beta}_1=\boldsymbol{\alpha}_1$ ， $\boldsymbol{\varepsilon}_1=\displaystyle\frac{\boldsymbol{\beta}_1}{|\boldsymbol{\beta}_1|}$
2. 令 $\boldsymbol{\beta}_2=\boldsymbol{\alpha}_2-\langle \boldsymbol{\alpha}_2,\boldsymbol{\varepsilon}_1\rangle \boldsymbol{\varepsilon}_1$ ， $\boldsymbol{\varepsilon}_2=\displaystyle\frac{\boldsymbol{\beta}_2}{|\boldsymbol{\beta}_2|}$
3. 令 $\boldsymbol{\beta}_{3}=\boldsymbol{\alpha}_{3}-\langle \boldsymbol{\alpha}_{3}, \boldsymbol{\varepsilon}_{2}\rangle \boldsymbol{\varepsilon}_{2}-\langle \boldsymbol{\alpha}_{3}, \boldsymbol{\varepsilon}_{1}\rangle \boldsymbol{\varepsilon}_{1}$ ， $\boldsymbol{\varepsilon}_3=\displaystyle\frac{\boldsymbol{\beta}_3}{|\boldsymbol{\beta}_3|}$
4. 依此类推， $\displaystyle\boldsymbol{\beta}_{m}=\boldsymbol{\alpha}_{m}-\sum_{i=1}^{m-1}\langle \boldsymbol{\alpha}_{m}, \boldsymbol{\varepsilon}_{i}\rangle \boldsymbol{\varepsilon}_{i}$ ， $\boldsymbol{\varepsilon}_m=\displaystyle\frac{\boldsymbol{\beta}_m}{|\boldsymbol{\beta}_m|}$ ， $m=2,3,\ldots,n$

---

正交化对应的过渡矩阵

$\left\{\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \ldots, \boldsymbol{\varepsilon}_{n}\right\}$ 到 $\left\{\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \ldots, \boldsymbol{\alpha}_{n}\right\}$ 的过渡矩阵

$$\boldsymbol{P}=\left[\begin{array}{cccc} \left|\boldsymbol{\beta}_{1}\right| & \langle \boldsymbol{\alpha}_{2}, {\boldsymbol{\varepsilon}_{1}\rangle } & \langle \boldsymbol{\alpha}_{3}, {\boldsymbol{\varepsilon}_{1}\rangle } & \cdots & \langle \boldsymbol{\alpha}_{n}, \boldsymbol{\varepsilon}_{1}\rangle \\ &{\left|\boldsymbol{\beta}_{2}\right|} & \langle \boldsymbol{\alpha}_{3}, {\boldsymbol{\varepsilon}_{2}\rangle } & {\cdots} & {\langle \boldsymbol{\alpha}_{n}, \boldsymbol{\varepsilon}_{2}\rangle } \\ && |\boldsymbol{\beta}_3|& \cdots & \langle \boldsymbol{\alpha}_{n}, {\boldsymbol{\varepsilon}_{3}\rangle }\\ &{} & {} & {\ddots}& \vdots\\ &{} & {} & & {\left|\boldsymbol{\beta}_{n}\right|}\end{array}\right]$$

• $\left\{\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \ldots, \boldsymbol{\alpha}_{n}\right\}=\left\{\boldsymbol{\varepsilon}_{1}, \boldsymbol{\varepsilon}_{2}, \ldots, \boldsymbol{\varepsilon}_{n}\right\} \boldsymbol{P}$

---

Schmidt 正交化的计算过程

例 设 $\mathbb{R}^3$ 的基

$$\boldsymbol{B}=\left\{\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\boldsymbol{\alpha}_3\right\}=\left\{\left[\begin{array}{l}{0} \\ {0} \\ {2}\end{array}\right], \left[\begin{array}{l}{4} \\ {3} \\ {1}\end{array}\right], \left[\begin{array}{r}{2} \\ {1} \\ {-2}\end{array}\right]\right\},$$

用 Schmidt 正交化方法求 $\mathbb{R}^3$ 的标准正交基.

---

提示

• $\boldsymbol{\beta}_{1}=\boldsymbol{\alpha}_{1}=\left[\begin{array}{l}{0} \\ {0} \\ {2}\end{array}\right],\left|\boldsymbol{\beta}_{1}\right|=2, \quad \boldsymbol{\varepsilon}_{1}=\frac{\boldsymbol{\beta}_{1}}{\left|\boldsymbol{\beta}_{1}\right|}=\left[\begin{array}{l}{0} \\ {0} \\ {1}\end{array}\right]$
• $\boldsymbol{\beta}_{2}=\boldsymbol{\alpha}_{2}-\langle \boldsymbol{\alpha}_{2}, \boldsymbol{\varepsilon}_{1}\rangle \boldsymbol{\varepsilon}_{1}=\left[\begin{array}{l}{4} \\ {3} \\ {0}\end{array}\right]$ ， $\boldsymbol{\varepsilon}_{2}=\frac{\boldsymbol{\beta}_{2}}{\left|\boldsymbol{\beta}_{2}\right|}=\frac{1}{5}\left[\begin{array}{l}{4} \\ {3} \\ {0}\end{array}\right]$
• $\boldsymbol{\beta}_{3}=\boldsymbol{\alpha}_{3}-\langle \boldsymbol{\alpha}_{3}, \boldsymbol{\varepsilon}_{2}\rangle \boldsymbol{\varepsilon}_{2}-\langle \boldsymbol{\alpha}_{3}, \boldsymbol{\varepsilon}_{1}\rangle \boldsymbol{\varepsilon}_{1}=\frac{1}{25}\left[\begin{array}{r}{6} \\ {-8} \\ {0}\end{array}\right]$ ， $\boldsymbol{\varepsilon}_{3}=\frac{\boldsymbol{\beta}_{3}}{\left|\boldsymbol{\beta}_{3}\right|}=\frac{1}{5}\left[\begin{array}{r}{3} \\ {-4} \\ {0}\end{array}\right]$
• $\left\{\boldsymbol{\varepsilon}_1,\boldsymbol{\varepsilon}_2,\boldsymbol{\varepsilon}_3\right\}=\left\{\left[\begin{array}{l}{0} \\ {0} \\ {1}\end{array}\right], \left[\begin{array}{c}{4 / 5} \\ {3 / 5} \\ {0}\end{array}\right], \left[\begin{array}{r}{3 / 5} \\ {-4 / 5} \\ {0}\end{array}\right]\right\}$

---

1.3.3 正交补空间

设 $W_1,W_2$ 都是内积空间 $V$ 的子空间，若对任意的 $\boldsymbol{\alpha}\in W_1,\boldsymbol{\beta}\in W_2$ ，都有 $\boldsymbol{\alpha}\perp\boldsymbol{\beta}$ ，则称 $W_1$ 与 $W_2$ 正交，记为 $W_1\perp W_2$ .

• 若 $W_1\perp W_2$ ，则 $W_1+W_2=W_1\oplus W_2$;
• 思考 在 $\mathbb{R}^3$ 中，两个过原点且相互垂直的平面，分别对应子空间 $W_1,W_2$ ，是否意味着 $W_1\perp W_2$ ？
  
  • 否！
  • 几何意义上的垂直和线性空间的正交不是严格等价的.

---

内积空间的正交直和分解

设 $W_1,W_2$ 都是内积空间 $V$ 的子空间，若有 $W_1\perp W_2$ ，且 $V=W_1\oplus W_2$ ，则称 $W_1$ 与 $W_2$ 互为 正交补空间 (Orthogonal Complementary Space)

• 记为$W_1=W_2^{\perp},\quad W_2=W_1^{\perp}$ .
• 称 $V=W_{1} \oplus W_{1}^{\perp}=W_{2} \oplus W_{2}^{\perp}$ 为 $V$ 的 正交直和分解 (Orthogonal Direct Sum Decomposition)

---

定理 内积空间的任一子空间都有唯一的正交补.

---

证明思路：

• 存在性
  
  • 设 $W_1\subset V^n$，$\mathrm{dim}(W_1)=r<n$.
  • 取 $\{\boldsymbol{\varepsilon}_1,\boldsymbol{\varepsilon}_2,...,\boldsymbol{\varepsilon}_r\}$ 为 $W_1$ 的标准正交基.
  • 利用基扩张定理，将 $W_1$ 的基扩充为 $V$ 的基 $\{\boldsymbol{\varepsilon}_1,...,\boldsymbol{\varepsilon}_r,\boldsymbol{\alpha}_{r+1},...,\boldsymbol{\alpha}_n\}$.
  • 保持前 $r$ 个向量不变，对以上的基从第 $r+1$ 个向量开始施以 Schmit 正交化，得到标准正交基 $\{\boldsymbol{\varepsilon}_{r+1},...,\boldsymbol{\varepsilon}_n\}$.
  • 记 $W_2=\mathrm{span}\{\boldsymbol{\varepsilon}_{r+1},...,\boldsymbol{\varepsilon}_n\}$，则 $W_2=W_1^{\perp}$

---

• 唯一性
  
  • 需要证明：$\forall\boldsymbol{\alpha}\notin W_1$，若满足 $\forall\boldsymbol{\beta}\in W_2,\;\langle\boldsymbol{\alpha},\boldsymbol{\beta}\rangle=0$，则必有 $\boldsymbol{\alpha}\in W_2$.
  • 反证法：若 $\boldsymbol{\alpha}\notin W_2$，则可将其分解为 $\boldsymbol{\alpha}=\boldsymbol{\alpha}_1+\boldsymbol{\alpha}_2$，其中 $\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2$ 分别为 $W_1,W_2$ 中的非零向量.
  • $\langle\boldsymbol{\alpha},\boldsymbol{\alpha}_2\rangle=\langle\boldsymbol{\alpha}_1+\boldsymbol{\alpha}_2,\boldsymbol{\alpha}_2\rangle=\langle\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2\rangle+\langle\boldsymbol{\alpha}_2,\boldsymbol{\alpha}_2\rangle=|\boldsymbol{\alpha}_2|^2>0$
  • 与假设矛盾.

---

求空间的正交补

例 设 $\boldsymbol{B}=\{\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3,\boldsymbol{e}_4,\boldsymbol{e}_5\}$ 是欧氏空间 $V^5$ 的标准正交基，令

$$\begin{align*} &\boldsymbol{\alpha}_{1}=\boldsymbol{e}_{1}+\boldsymbol{e}_{5},\\ &\boldsymbol{\alpha}_{2}=\boldsymbol{e}_{1}-\boldsymbol{e}_{2}+\boldsymbol{e}_{4},\\ &\boldsymbol{\alpha}_{3}=2 \boldsymbol{e}_{1}+\boldsymbol{e}_{2}+\boldsymbol{e}_{3}. \end{align*}$$

(1) 求 ${W}=\operatorname{span}\left\{\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}\right\}$ 的标准正交基;
(2) 求 $W$ 的正交补.

---

提示 (1) 利用 Schmit 正交化方法及勾股定理

• $|\boldsymbol{\alpha}_1|=|\boldsymbol{e}_1+\boldsymbol{e}_5|=\sqrt{|\boldsymbol{e}_1|^2+|\boldsymbol{e}_5|^2}=\sqrt{2}$
• 从而 $\boldsymbol{\varepsilon}_1=\frac{\boldsymbol{\beta}_1}{|\boldsymbol{\beta}_1|}=\frac{\boldsymbol{\alpha}_1}{|\boldsymbol{\alpha}_1|}=\frac{1}{\sqrt{2}}(\boldsymbol{e}_1+\boldsymbol{e}_5)$
• $\langle\boldsymbol{\alpha}_2,\boldsymbol{\varepsilon}_1\rangle=\left\langle\boldsymbol{e}_{1}-\boldsymbol{e}_{2}+\boldsymbol{e}_{4},\frac{1}{\sqrt{2}}(\boldsymbol{e}_1+\boldsymbol{e}_5)\right\rangle$
  
  • $=\frac{1}{\sqrt{2}}\bigg(\langle\boldsymbol{e}_1,\boldsymbol{e}_1\rangle+\langle\boldsymbol{e}_1,\boldsymbol{e}_5\rangle-\langle\boldsymbol{e}_2,\boldsymbol{e}_1\rangle-\langle\boldsymbol{e}_2,\boldsymbol{e}_5\rangle+\langle\boldsymbol{e}_4,\boldsymbol{e}_1\rangle+\langle\boldsymbol{e}_4,\boldsymbol{e}_5\rangle\bigg)$
  • $={1}/{\sqrt{2}}$

---

• $\boldsymbol{\beta}_2=\boldsymbol{\alpha}_2-\langle\boldsymbol{\alpha}_2,\boldsymbol{\varepsilon}_1\rangle\boldsymbol{\varepsilon}_1$
  
  • $=\boldsymbol{e}_{1}-\boldsymbol{e}_{2}+\boldsymbol{e}_{4}-\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\boldsymbol{e}_1+\boldsymbol{e}_5)$
  • $=\frac{1}{2}(\boldsymbol{e}_1-2\boldsymbol{e}_2+2\boldsymbol{e}_4-\boldsymbol{e}_5)$
• $|\boldsymbol{\beta}_2|=\frac{1}{2}\sqrt{|\boldsymbol{e}_1|^2+4|\boldsymbol{e}_2|^2+4|\boldsymbol{e}_4|^2+|\boldsymbol{e}_5|^2}=\frac{\sqrt{10}}{2}$
• 于是 $\boldsymbol{\varepsilon}_2=\frac{\boldsymbol{\beta}_2}{|\boldsymbol{\beta}_2|}=\frac{1}{\sqrt{10}}(\boldsymbol{e}_1-2\boldsymbol{e}_2+2\boldsymbol{e}_4-\boldsymbol{e}_5)$
• 同理计算可得，$\boldsymbol{\varepsilon}_{3}=\frac{1}{2}\left(\boldsymbol{e}_{1}+\boldsymbol{e}_{2}+\boldsymbol{e}_{3}-\boldsymbol{e}_{5}\right)$

---

• (2) 设 $\boldsymbol{\beta}\in W^{\perp}$ ， $\boldsymbol{\beta}=x_{1} \boldsymbol{e}_{1}+x_{2} \boldsymbol{e}_{2}+x_{3} \boldsymbol{e}_{3}+x_{4} \boldsymbol{e}_{4}+x_{5} \boldsymbol{e}_{5}$
• 由 $\langle \boldsymbol{\beta}, \boldsymbol{\varepsilon}_{i}\rangle =0, \quad i=1,2,3$
  
  • $\left\{\begin{array}{l}{\frac{1}{\sqrt{2}} x_{1}+\frac{1}{\sqrt{2}} x_{5}=0} \\ {\frac{1}{\sqrt{10}} x_{1}-\frac{2}{\sqrt{10}} x_{2}+\frac{2}{\sqrt{10}} x_{4}-\frac{1}{\sqrt{10}} x_{5}=0} \\ {\frac{1}{2} x_{1}+\frac{1}{2} x_{2}+\frac{1}{2} x_{3}-\frac{1}{2} x_{5}=0}\end{array}\right.$
  • $\left[\begin{array}{ccccc}{1} & {0} & {0} & {0} & {1} \\ {1} & {-2} & {0} & {2} & {-1} \\ {1} & {1} & {1} & {0} & {-1}\end{array}\right] \rightarrow\left[\begin{array}{ccccc}{1} & {0} & {0} & {0} & {1} \\ {0} & {1} & {0} & {-1} & {1} \\ {0} & {0} & {1} & {1} & {-3}\end{array}\right]$
  • 基础解系： $\left[\begin{array}{lllll}{-1} & {-1} & {3} & {0} & {1}\end{array}\right]^{\mathrm{T}}$ ， $\left[\begin{array}{lllll}{0} & {1} & {-1} & {1} & {0}\end{array}\right]^{\mathrm{T}}$
• $W^{\perp}=\mathrm{span}\{-\boldsymbol{e}_{1}-\boldsymbol{e}_{2}+3 \boldsymbol{e}_{3}+\boldsymbol{e}_{5},\boldsymbol{e}_{2}-\boldsymbol{e}_{3}+\boldsymbol{e}_{4}\}$

---

Gram–Schmidt Process[1]

• The method is named after Jørgen Pedersen Gram(1850-1916) and Erhard Schmidt(1876-1959), but Pierre-Simon Laplace(1749-1827) had been familiar with it before Gram and Schmidt. In the theory of Lie group decompositions it is generalized by the Iwasawa(1917-1998) decomposition(岩泽分解).

---

1.3.4 正交变换与对称变换

---

正交变换

设 $T$ 是欧式空间 $V^n$ 上的线性变换，若对任意的 $\boldsymbol{\alpha},\boldsymbol{\beta}\in V^n$ ，有

$$\langle T\boldsymbol{\alpha},T\boldsymbol{\beta}\rangle =\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle$$

称 $T$ 为 $V^n$ 上的 正交变换 (Orthogonal Transformation)

---

正交变换的判定

定理 1.3.5 设 $T$ 是欧式空间 $V^n$ 上的线性变换，则下列条件等价：

1. $T$ 是正交变换;
2. $T$ 保持向量长度不变，即对任意的 $\boldsymbol{\alpha}\in V^n$ ，有 $|T\boldsymbol{\alpha}|=|\boldsymbol{\alpha}|$ ;
3. $T$ 将标准正交基映射为标准正交基;
4. $T$ 在标准正交基下的矩阵为正交矩阵.
   
   • $\boldsymbol{A}$ 为正交阵，当且仅当 $\boldsymbol{A}\boldsymbol{A}^{\mathrm{T}}=\boldsymbol{I}$ 或 $\boldsymbol{A}^{\mathrm{T}}\boldsymbol{A}=\boldsymbol{I}$.
   • 正交矩阵的行（列）向量两两正交，且均为单位向量.

---

证明

• $\bbox[lightgrey]{1.\Rightarrow2.}$ $\langle {T} {\boldsymbol{\alpha}}, {T} {\boldsymbol{\alpha}}\rangle =\langle {\boldsymbol{\alpha}}, {\boldsymbol{\alpha}}\rangle$ ，即 $|T\boldsymbol{\alpha}|=|\boldsymbol{\alpha}|$
• $\bbox[lightgrey]{2.\Rightarrow3.}$ 设 $\{\boldsymbol{\varepsilon}_1,\boldsymbol{\varepsilon}_2,\ldots,\boldsymbol{\varepsilon}_n\}$ 是标准正交基.
  
  • $\left|{T} \boldsymbol{\varepsilon}_{i}+{T} \boldsymbol{\varepsilon}_{j}\right|=\left|{T}\left(\boldsymbol{\varepsilon}_{i}+\boldsymbol{\varepsilon}_{j}\right)\right|=\left|\boldsymbol{\varepsilon}_{i}+\boldsymbol{\varepsilon}_{j}\right|=\left\{\begin{array}{cc}2,& i=j\\ \sqrt{2},& i\ne j\end{array}\right.$
  • $\left|{T} \boldsymbol{\varepsilon}_{i}+{T} \boldsymbol{\varepsilon}_{j}\right|^2= \langle T\boldsymbol{\varepsilon}_i+T\boldsymbol{\varepsilon}_j,T\boldsymbol{\varepsilon}_i+T\boldsymbol{\varepsilon}_j\rangle$
    
    • $=|T\boldsymbol{\varepsilon}_i|^2+|T\boldsymbol{\varepsilon}_j|^2+2\langle T\boldsymbol{\varepsilon}_i,T\boldsymbol{\varepsilon}_j\rangle=2+2\langle T\boldsymbol{\varepsilon}_i,T\boldsymbol{\varepsilon}_j\rangle$
  • 故 $\langle {T} \boldsymbol{\varepsilon}_{i}, {T} \boldsymbol{\varepsilon}_{j}\rangle =\delta_{i j}=\left\{\begin{array}{ll}{1,} & {i=j} \\ {0,} & {i \neq j}\end{array}\right.$
  • 这说明 $\{T\boldsymbol{\varepsilon}_1,T\boldsymbol{\varepsilon}_2,\ldots,T\boldsymbol{\varepsilon}_n\}$ 也是标准正交基.

---

• $\bbox[lightgrey]{3.\Rightarrow1.}$
  
  • $\bbox[lightgrey]{3.\Rightarrow1.}$
  • 设 $\boldsymbol{B}$ 是标准正交基，则 $T\boldsymbol{B}$ 也是标准正交基
  • 二者的度量矩阵均为 $\boldsymbol{G}=\boldsymbol{I}$
  • $\forall\boldsymbol{\alpha}=\boldsymbol{Bx},\boldsymbol{\beta}=\boldsymbol{By}\in V^n$
  • $\langle\boldsymbol{\alpha},\boldsymbol{\beta}\rangle=\boldsymbol{x}^{\mathrm{T}}\boldsymbol{G}\boldsymbol{y}=\boldsymbol{x}^{\mathrm{T}}\boldsymbol{y}$
  • $\langle T\boldsymbol{\alpha},T\boldsymbol{\beta}\rangle=\langle T\boldsymbol{Bx},T\boldsymbol{By}\rangle=\langle (T\boldsymbol{B})\boldsymbol{x},(T\boldsymbol{B})\boldsymbol{y}\rangle=\boldsymbol{x}^{\mathrm{T}}\boldsymbol{G}\boldsymbol{y}=\boldsymbol{x}^{\mathrm{T}}\boldsymbol{y}=\langle\boldsymbol{\alpha},\boldsymbol{\beta}\rangle$

---

• $\bbox[lightgrey]{3.\Leftrightarrow 4.}$
  
  • 设 $\boldsymbol{B}=\{\boldsymbol{\varepsilon}_1,\boldsymbol{\varepsilon}_2,\ldots,\boldsymbol{\varepsilon}_n\}$ 是标准正交基，$T$ 在 $\boldsymbol{B}$ 下的矩阵为 $\boldsymbol{A}$
  • 记 $\boldsymbol{A}=[\boldsymbol{A}_1\;\;\boldsymbol{A}_2\;...\;\boldsymbol{A}_n]$
    
    • $T\boldsymbol{\varepsilon_i}=\boldsymbol{BA}_i$，$i=1,...,n$
  • $\langle T\boldsymbol{\varepsilon}_i,T\boldsymbol{\varepsilon}_j\rangle=\left\langle \boldsymbol{BA}_i,\boldsymbol{BA}_j\right\rangle=\boldsymbol{A}_i^{\mathrm{T}}\boldsymbol{A}_j$
  • $\langle T\boldsymbol{\varepsilon}_i,T\boldsymbol{\varepsilon}_j\rangle=\delta_{ij}$，当且仅当 $\boldsymbol{A}_i^{\mathrm{T}}\boldsymbol{A}_j=\delta_{ij}$
  • 故 $T\boldsymbol{B}$ 是标准正交基等价于 $\boldsymbol{A}$ 是正交阵.

---

常用的正交变换：旋转变换

---

二维平面上的旋转

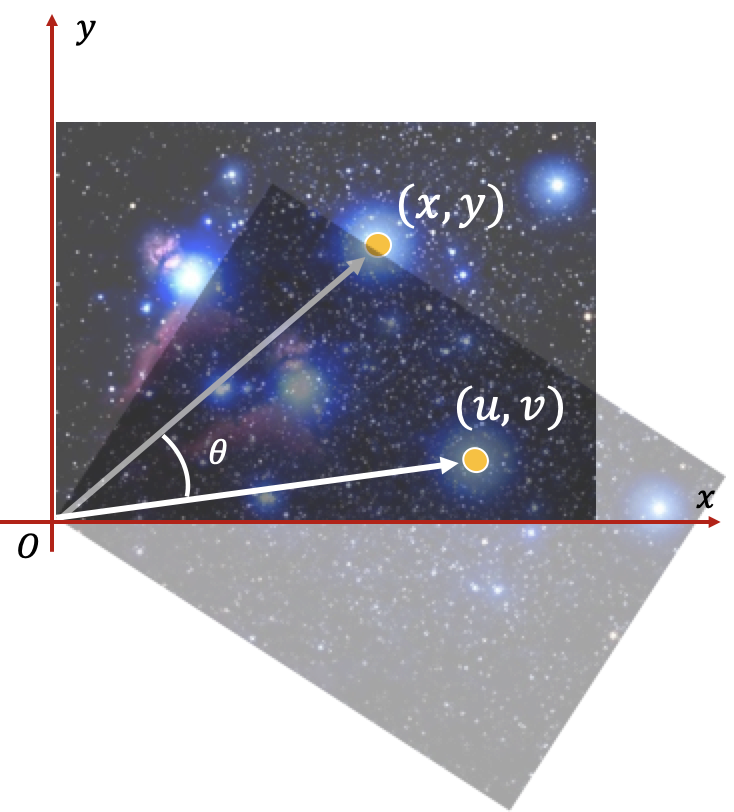
设 $\begin{bmatrix} x \\ y\end{bmatrix}=r\begin{bmatrix} \cos\phi \\ \sin\phi\end{bmatrix}$ ，

• $\begin{bmatrix} u \\ v\end{bmatrix}=r\begin{bmatrix} \cos(\phi-\theta) \\ \sin(\phi-\theta)\end{bmatrix}= \begin{bmatrix} x\cos\theta+y\sin\theta \\ y\cos\theta-x\sin\theta\end{bmatrix}=\left[\begin{array}{cc}{\cos \theta} & {\sin \theta} \\ {-\sin \theta} & {\cos \theta}\end{array}\right]\left[\begin{array}{l}{x} \\ {y}\end{array}\right]$

---

二维欧式空间中的旋转变换

取定二维欧式空间中的标准正交基 $\boldsymbol{B}=\{\boldsymbol{\varepsilon}_1,\boldsymbol{\varepsilon}_2\}$ ，绕零向量顺时针旋转 $\theta$ 角的线性变换 $T$ 在 $\boldsymbol{B}$ 下的矩阵为

$$T(\theta)=\left[\begin{array}{cc}{\cos \theta} & {\sin \theta} \\ {-\sin \theta} & {\cos \theta}\end{array}\right]$$

• 顺时针方向 由 $\boldsymbol{\varepsilon}_2$ 指向 $\boldsymbol{\varepsilon}_1$ 的方向
• 绕零向量逆时针旋转 $T(-\theta)=\left[\begin{array}{cc}{\cos \theta} & {-\sin \theta} \\ {\sin \theta} & {\cos \theta}\end{array}\right]$
• $[T(\theta)]^{\mathrm{T}}=T(-\theta)=[T(\theta)]^{-1}$
  
  • 从而已知 $[T(\theta)]^{\mathrm{T}}T(\theta)=T(\theta)[T(\theta)]^{\mathrm{T}}=I$

---

高维空间中的旋转变换

取定 $V^n$ 的标准正交基 $\boldsymbol{B}=\{\boldsymbol{\varepsilon}_1,\ldots,\boldsymbol{\varepsilon}_n\}$，子空间 $\mathrm{span}\{\boldsymbol{\varepsilon}_i,\boldsymbol{\varepsilon}_j\}$ 中绕零向量顺时针旋转 $\theta$ 角的变换称为 初等旋转变换，其在 $\boldsymbol{B}$ 下的矩阵为

$$T_{ij}(\theta)=\left[\begin{array}{cccccccccc} 1\\ &\ddots\\ &&1\\ &&&\cos\theta &&&&&\sin\theta \\ &&&&1\\ &&&&&&\ddots\\ &&&&&&&1\\ &&&-\sin\theta &&&&&\cos\theta &&&\\ &&&&&&&&&1\\ &&&&&&&&&&\ddots\\ &&&&&&&&&&&1 \end{array}\right] \begin{array}{cc} \\ \\ \\ \leftarrow & \text{第}i\text{行} \\ \\ \\ \\ \leftarrow & \text{第}j\text{行} \\ \\ \\ \\ \end{array}$$

---

常用的正交变换：镜像变换（Householder Reflection）

• 取定过原点的一条直线 $l$
  
  • 取 $\boldsymbol{\omega}$ 为与 $l$ 垂直的单位向量
• 任取向量 $\boldsymbol{\alpha}$
• $\boldsymbol{\alpha}$ 关于直线 $l$ 对称的向量
  
  • $T\boldsymbol{\alpha}=\boldsymbol{\alpha}-2\langle\boldsymbol{\omega},\boldsymbol{\alpha}\rangle\boldsymbol{\omega}$
• 几何上， $\langle\boldsymbol{\omega},\boldsymbol{\alpha}\rangle$ 表示 $\boldsymbol{\alpha}$ 在 $\boldsymbol{\omega}$ 上的投影长度

---

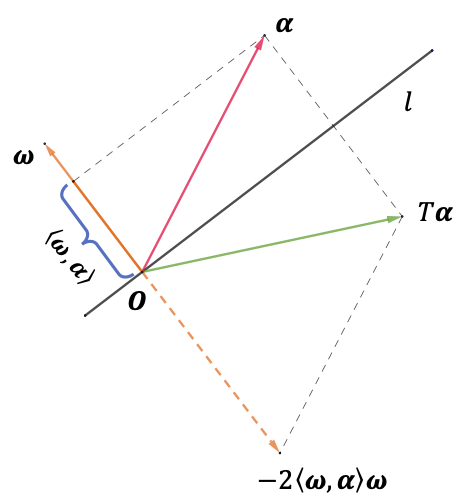
镜像变换对应的矩阵

在欧式空间中 $\mathbb{R}^n$ 中，若定义 $\langle\boldsymbol{\alpha},\boldsymbol{\beta}\rangle=\boldsymbol{\alpha}^{\mathrm{T}}\boldsymbol{\beta}$，则镜像变换可表示为

$$\boldsymbol{H}_{\boldsymbol{\omega}}\boldsymbol{\alpha}=(\boldsymbol{I}-2\boldsymbol{\omega}\boldsymbol{\omega}^{\mathrm{T}})\boldsymbol{\alpha}$$

• $\boldsymbol{H}_{{\omega}}^{\mathrm{T}}=\boldsymbol{H}_{{\omega}}$
• $\boldsymbol{H}_{{\omega}}^2=\boldsymbol{I}$
• $\boldsymbol{H}_{{\omega}}$ 是正交阵

---

例 已知向量

$$\boldsymbol{\alpha}=\begin{bmatrix}1 \\ 2 \\ 0\end{bmatrix},\quad \boldsymbol{\beta}=\begin{bmatrix}0 \\ 2 \\ 4\end{bmatrix}$$

求 Householder 变换矩阵 $\boldsymbol{H}$，使得 $\boldsymbol{H\alpha}=k\boldsymbol{\beta}$，其中 $k$ 为正实数，给出 $k$ 的值.

---

解 将 $\boldsymbol{\alpha},\boldsymbol{\beta}$ 分别单位化 $\boldsymbol{\alpha}_0=\dfrac{1}{\sqrt{5}}[1\;\;2\;\;0]^{\mathrm{T}}$，$\boldsymbol{\beta}_0=\dfrac{1}{\sqrt{5}}[0\;\;1\;\;2]^{\mathrm{T}}$.

令 $\boldsymbol{\omega}=\dfrac{\boldsymbol{\beta}_0-\boldsymbol{\alpha}_0}{|\boldsymbol{\beta}_0-\boldsymbol{\alpha}_0|}=\dfrac{1}{\sqrt{6}}[-1\;\;-1\;\;2]^{\mathrm{T}}$.

$\boldsymbol{H}=\boldsymbol{I}_3-2\boldsymbol{\omega}\boldsymbol{\omega}^{\mathrm{T}}=\dfrac{1}{3}\begin{bmatrix} 2 & -1 & 2 \\ -1 & 2 & 2 \\ 2 & 2 & -1\end{bmatrix}$，即为所求 Householder 矩阵.

$\boldsymbol{H\alpha}=[0\;\;1\;\;2]^{\mathrm{T}}=\dfrac{1}{2}\boldsymbol{\beta}$，故 $k=\dfrac{1}{2}$.

---

注： 任意两个向量 $\boldsymbol{x},\boldsymbol{y}$，只要 $|\boldsymbol{x}|=|\boldsymbol{y}|$，则一定存在 Householder 矩阵 $\boldsymbol{H}$，使得 $\boldsymbol{y}=\boldsymbol{H}\boldsymbol{x}$.

• 事实上，因为 $\boldsymbol{x}^{\mathrm{T}}\boldsymbol{x}=|\boldsymbol{x}|^2=|\boldsymbol{y}|^2=\boldsymbol{y}^{\mathrm{T}}\boldsymbol{y}$
• 易得 $(\boldsymbol{x}-\boldsymbol{y})^{\mathrm{T}}(\boldsymbol{x}+\boldsymbol{y})=0$
• 故 $\displaystyle\frac{\boldsymbol{x}-\boldsymbol{y}}{|\boldsymbol{x}-\boldsymbol{y}|}$ 就是 Householder 所需变换指向 $\boldsymbol{x}$ 一侧的单位法向量
• 进而，由 Householder 矩阵的构造公式计算可得 $\displaystyle\boldsymbol{H}=\boldsymbol{I}-\frac{2(\boldsymbol{x}-\boldsymbol{y})(\boldsymbol{x}-\boldsymbol{y})^{\mathrm{T}}}{|\boldsymbol{x}-\boldsymbol{y}|^2}=\boldsymbol{I}-\frac{2(\boldsymbol{x}-\boldsymbol{y})(\boldsymbol{x}-\boldsymbol{y})^{\mathrm{T}}}{(\boldsymbol{x}-\boldsymbol{y})^{\mathrm{T}}(\boldsymbol{x}-\boldsymbol{y})}$

---

对称变换

设 $T$ 是欧氏空间 $V$ 上的线性变换，若 $\forall\boldsymbol{\alpha},\boldsymbol{\beta}\in V$ 有

$$\langle T\boldsymbol{\alpha},\boldsymbol{\beta}\rangle =\langle \boldsymbol{\alpha},T\boldsymbol{\beta}\rangle$$

则称 $T$ 为 对称变换.(Symmetry Transform)

---

对称变换对应的矩阵

• 定理1.3.6 $T$ 是对称变换，当且仅当 $T$ 在标准正交基下的矩阵是对称矩阵.
• 对称矩阵的不同特征值对应的特征向量是正交的.
  
  • 对称矩阵的特征子空间两两正交.
  • 对称矩阵的全部特征子空间构成了内积空间的正交直和分解.

---

注： 对称矩阵的不同特征值对应的特征向量是正交的

• 设 $\boldsymbol{A}=\boldsymbol{A}^{\mathrm{T}}$，$\lambda_1,\lambda_2$ 为 $\boldsymbol{A}$ 的特征值，$\lambda_1\ne\lambda_2$， $\boldsymbol{\xi}_1,\boldsymbol{\xi}_2$ 分别为 $\lambda_1,\lambda_2$ 对应的特征向量
• $\lambda_1\langle \boldsymbol{\xi}_1,\boldsymbol{\xi}_2\rangle =\langle \lambda_1\boldsymbol{\xi}_1,\boldsymbol{\xi}_2\rangle =\langle A\boldsymbol{\xi}_1,\boldsymbol{\xi}_2\rangle=\langle \boldsymbol{\xi}_1,A\boldsymbol{\xi}_2\rangle =\langle \boldsymbol{\xi}_1,\lambda_2\boldsymbol{\xi}_2\rangle =\lambda_2\langle \boldsymbol{\xi}_1,\boldsymbol{\xi}_2\rangle$
• $\lambda_1\ne\lambda_2$，故必有$\langle \boldsymbol{\xi}_1,\boldsymbol{\xi}_2\rangle =0$

---

例 在 $\mathbb{R}^{2\times 2}$ 中定义内积

$$\displaystyle\langle \boldsymbol{A}, \boldsymbol{B}\rangle =\sum_{i=1}^{2} \sum_{j=1}^{2} a_{i j} b_{i j}, \quad \boldsymbol{A}=\left[a_{ij}\right]_{2\times 2}, \quad \boldsymbol{B}=\left[b_{ij}\right]_{2\times 2}$$

考虑 $\mathbb{R}^{2\times2}$ 的子空间 $V=\left\{\left[\begin{array}{ll}{x_{1}} & {x_{2}} \\ {x_{3}} & {x_{4}}\end{array}\right] \bigg| x_{3}-x_{4}=0\right\}$ 及其上的线性变换 $T$ ：

$$\boldsymbol{T X}=\boldsymbol{X}\left[\begin{array}{ll}{1} & {2} \\ {2} & {1}\end{array}\right]$$

(1) 求 $V$ 上的一个标准正交基;
(2) 证明 $T$ 是对称变换;
(3) 求 $V$ 上的标准正交基，使得 $T$ 在该基下的矩阵是对角阵.

---

提示

• 取标准正交基：
  
  • $\boldsymbol{E}_{1}=\left[\begin{array}{ll}{1} & {0} \\ {0} & {0}\end{array}\right], \boldsymbol{E}_{2}=\left[\begin{array}{ll}{0} & {1} \\ {0} & {0}\end{array}\right],\boldsymbol{E}_{3}=\frac{1}{\sqrt{2}}\left[\begin{array}{ll}{0} & {0} \\ {1} & {1}\end{array}\right]$
• $T$ 在 $\{\boldsymbol{E}_1,\boldsymbol{E}_2,\boldsymbol{E}_3\}$ 下的矩阵： $\boldsymbol{A}=\left[\begin{array}{lll}{1} & {2} & {0} \\ {2} & {1} & {0} \\ {0} & {0} & {3}\end{array}\right]$

---

• 求 $\boldsymbol{A}$ 的特征值和特征向量
  
  • $|\lambda \boldsymbol{I}-\boldsymbol{A}|=\left|\begin{array}{ccc}{\lambda-1} & {-2} & {0} \\ {-2} & {\lambda-1} & {0} \\ {0} & {0} & {\lambda-3}\end{array}\right|=(\lambda+1)(\lambda-3)^{2}$
  • $\boldsymbol{A}$ 的特征值： $\lambda_{1}=-1, \quad \lambda_{2}=\lambda_{3}=3$
  • 对应的特征向量： $\boldsymbol{X}_{1}=\frac{1}{\sqrt{2}}\left[\begin{array}{c}{1} \\ {-1} \\ {0}\end{array}\right],\quad \boldsymbol{X}_{2}=\frac{1}{\sqrt{2}}\left[\begin{array}{l}{1} \\ {1} \\ {0}\end{array}\right], \quad \boldsymbol{X}_{3}=\left[\begin{array}{l}{0} \\ {0} \\ {1}\end{array}\right]$
• $V$ 的标准正交基： $\boldsymbol{\varepsilon}_i=\{\boldsymbol{E}_1,\boldsymbol{E}_2,\boldsymbol{E}_3\}\boldsymbol{X}_i,\;i=1,2,3$
  
  • $\boldsymbol{\varepsilon}_1=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}{1} & {-1} \\ {0} & {0}\end{array}\right],\quad \boldsymbol{\varepsilon}_2=\frac{1}{\sqrt{2}}\left[\begin{array}{ll}{1} & {1} \\ {0} & {0}\end{array}\right], \quad\boldsymbol{\varepsilon}_3= \frac{1}{\sqrt{2}}\left[\begin{array}{ll}{0} & {0} \\ {1} & {1}\end{array}\right]$
• $T$ 在 $\{\boldsymbol{\varepsilon}_1,\boldsymbol{\varepsilon}_2,\boldsymbol{\varepsilon}_3\}$ 下的矩阵为 $\mathrm{diag}\{-1,3,3\}$

---

1.3.5 酉变换与酉对称变换

设 $T$ 是酉空间 $V$ 上的线性变换，若 $\forall\boldsymbol{\alpha},\boldsymbol{\beta}\in V$ 有

$$\langle T\boldsymbol{\alpha},T\boldsymbol{\beta}\rangle =\langle \boldsymbol{\alpha},\boldsymbol{\beta}\rangle$$

则称 $T$ 为 酉变换.(Unitary Transformation)

• 设 $\boldsymbol{A}$ 是 $n$ 阶复方阵，若$\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}=\boldsymbol{AA}^{\mathrm{H}}=\boldsymbol{I}$，则称 $\boldsymbol{A}$ 为 酉矩阵.(Unitary Matrix)
• 酉变换和酉矩阵是分别是欧式空间中的正交变换和正交矩阵的推广

---

酉变换的判定

定理 1.3.5' 设 $T$ 是酉空间 $V^n$ 上的线性变换，则下列条件等价：

1. $T$ 是酉变换;
2. $T$ 保持向量长度不变，即对任意的 $\boldsymbol{\alpha}\in V^n$ ，有 $|T\boldsymbol{\alpha}|=|\boldsymbol{\alpha}|$ ;
3. $T$ 将标准正交基映射为标准正交基;
4. $T$ 在标准正交基下的矩阵为酉矩阵.

---

酉对称变换

设 $T$ 是酉空间 $V$ 上的线性变换，若 $\forall\boldsymbol{\alpha},\boldsymbol{\beta}\in V$ 有

$$\langle T\boldsymbol{\alpha},\boldsymbol{\beta}\rangle =\langle \boldsymbol{\alpha},T\boldsymbol{\beta}\rangle$$

则称 $T$ 为 酉对称变换.

• 设 $\boldsymbol{A}$ 是 $n$ 阶复方阵，若 $\boldsymbol{A}^{\mathrm{H}}=\boldsymbol{A}$，则称 $\boldsymbol{A}$ 为 Hermite 矩阵.
• 定理1.3.6' $T$ 是酉对称变换，当且仅当 $T$ 在标准正交基下的矩阵是 Hermite 矩阵.

---

Schur定理

设 $\boldsymbol{A}$ 是 $n$ 阶复方阵，则存在一酉矩阵 $\boldsymbol{U}$ ，使得 $\boldsymbol{U}^{-1}\boldsymbol{AU}$ 是上三角矩阵，即

$$\boldsymbol{U}^{-1}\boldsymbol{AU}=\boldsymbol{U}^{\mathrm{H}}\boldsymbol{AU}=\left[ \begin{array}{cccc} {\lambda_{1}} & {*} & {\cdots} & {*} \\ & {\lambda_{2}} & {\cdots} & {*} \\ & & {\ddots} & {\vdots} \\ & & & {\lambda_{n}} \end{array} \right]$$

其中 $\lambda_1,\lambda_2,\ldots,\lambda_n$ 是 $\boldsymbol{A}$ 的特征值.

---

证明思路 (数学归纳法)

• 设 $\boldsymbol{A}\boldsymbol{u}_1=\lambda_1\boldsymbol{u}_1$，其中 $\boldsymbol{u}_1$ 为单位向量.
• 将 $\boldsymbol{u}_1$ 扩张成 $\mathbb{C}^n$ 的标准正交基 $\{\boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_n\}$
  
  • 则 $\boldsymbol{U}_1=[\boldsymbol{u}_1\;\boldsymbol{u}_2\;\ldots\;\boldsymbol{u}_n]$ 是酉矩阵
• $\boldsymbol{A U}_{1}=\left[\boldsymbol{A} \boldsymbol{u}_{1}\; \boldsymbol{A} \boldsymbol{u}_{2} \cdots \boldsymbol{A} \boldsymbol{u}_{n}\right]$
  
  • $=[\boldsymbol{u}_1\;\boldsymbol{u}_2\;\ldots\;\boldsymbol{u}_n]\left[\begin{array}{cc}{\lambda_{1}} & {*} \\ \boldsymbol{0} & {\boldsymbol{A}_{1}}\end{array}\right]=\boldsymbol{U}_{1}\left[\begin{array}{cc}{\lambda_{1}} & {*} \\ \boldsymbol{0} & {\boldsymbol{A}_{1}}\end{array}\right]$
  • $\boldsymbol{A}_1$ 为 $n-1$ 阶方阵
• 以下使用数学归纳法证明.

---

• $n=1$ 时，$\boldsymbol{U}_1^{-1} \boldsymbol{A U}_1=\boldsymbol{U}_1^{\mathrm{H}} \boldsymbol{A U}_1=[\lambda_1]$ 为上三角阵，结论成立.
• $n>1$ 时，假设对 $n-1$ 阶方阵 $\boldsymbol{A}_1$ ，存在 $n-1$ 阶酉矩阵 $\boldsymbol{V}$ ，使得 $\boldsymbol{B}=\boldsymbol{V}^{-1}\boldsymbol{A}_1\boldsymbol{V}=\boldsymbol{V}^{\mathrm{H}}\boldsymbol{A}_1\boldsymbol{V}$ 为上三角阵.
• 令 $\boldsymbol{U}_{2}=\left[\begin{array}{ll}{1} & \boldsymbol{0} \\ \boldsymbol{0} & {\boldsymbol{V}}\end{array}\right]$，则 $\boldsymbol{U}=\boldsymbol{U}_1\boldsymbol{U}_2$ 也是酉矩阵
• $\boldsymbol{A U}=\boldsymbol{A}\boldsymbol{U}_1\boldsymbol{U}_2=\boldsymbol{U}_1\left[\begin{array}{cc}{\lambda_{1}} & {*} \\ \boldsymbol{0} & {\boldsymbol{A}_{1}}\end{array}\right]\left[\begin{array}{ll}{1} & \boldsymbol{0} \\ \boldsymbol{0} & {\boldsymbol{V}}\end{array}\right]=\boldsymbol{U}_1\left[\begin{array}{cc}{\lambda_{1}} & {*} \\ \boldsymbol{0} & \boldsymbol{A}_1\boldsymbol{V}\end{array}\right]$
  
  • $=\boldsymbol{U}_1\left[\begin{array}{cc}{\lambda_{1}} & {*} \\ \boldsymbol{0} & \boldsymbol{VB}\end{array}\right]=\boldsymbol{U}_1\boldsymbol{U}_2\left[\begin{array}{cc}{\lambda_{1}} & {*} \\ \boldsymbol{0} & \boldsymbol{B}\end{array}\right]=\boldsymbol{U}\left[\begin{array}{cc}{\lambda_{1}} & {*} \\ \boldsymbol{0} & \boldsymbol{B}\end{array}\right]$
• 即 $\boldsymbol{U}^{-1} \boldsymbol{A U}=\boldsymbol{U}^{\mathrm{H}} \boldsymbol{A U}=\left[\begin{array}{cc}{\lambda_{1}} & {*} \\ \boldsymbol{0} & \boldsymbol{B}\end{array}\right]$ 为上三角阵.

---

• 下面说明 $\left[\begin{array}{cc}{\lambda_{1}} & {*} \\ \boldsymbol{0} & \boldsymbol{B}\end{array}\right]$ 的对角元为 $\lambda_1,\lambda_2,...,\lambda_n$.
• 这等价于说明 $\lambda_2,...,\lambda_n$ 恰为 $\boldsymbol{B}$ 的特征值.
• 事实上，注意到 $\boldsymbol{A}\sim \left[\begin{array}{cc}{\lambda_{1}} & {*} \\ \boldsymbol{0} & \boldsymbol{B}\end{array}\right]$，故有
  
  • $|\lambda\boldsymbol{I}_n-\boldsymbol{A}|=\mathrm{det}\left(\left[\begin{array}{cc}{\lambda_{1}} & {*} \\ \boldsymbol{0} & \boldsymbol{B}\end{array}\right]\right)=(\lambda-\lambda_1)|\lambda\boldsymbol{I}_{n-1}-\boldsymbol{B}|$
• 上式意味着等式两边的根相同，由此可知 $\boldsymbol{B}$ 的特征多项值恰为为 $\boldsymbol{A}$ 的特征值 $\lambda_2,...,\lambda_n$.

---

Hermite 矩阵必可以相似对角化

推论 若 $\boldsymbol{A}$ 是 Hermite 矩阵，则存在一酉矩阵 $\boldsymbol{U}$ ，使得

$$\boldsymbol{U}^{-1} \boldsymbol{A U}=\boldsymbol{U}^{\mathrm{H}} \boldsymbol{A U}=\left[ \begin{array}{cccc} {\lambda_{1}} & & & \\ & {\lambda_{2}} & & \\ & & {\ddots} & \\ & & & {\lambda_{n}} \end{array} \right]$$

其中 $\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}$ 均为实数是 $\boldsymbol{A}$ 的全部特征值.

---

实对称矩阵必可以相似对角化

推论 若 $\boldsymbol{A}$ 是实对称矩阵，则存在一正交矩阵 $\boldsymbol{Q}$ ，使得

$$\boldsymbol{Q}^{-1} \boldsymbol{A Q}=\boldsymbol{Q}^{\mathrm{T}} \boldsymbol{A Q}=\left[ \begin{array}{cccc} {\lambda_{1}} & & & \\ & {\lambda_{2}} & & \\ & & {\ddots} & \\ & & & {\lambda_{n}} \end{array} \right]$$

其中 $\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}$ 均为实数是 $\boldsymbol{A}$ 的全部特征值.

• 定理 对称变換(酉对称变换)一定可以对角化，且其特征值均为实数.

---

附注：实方阵的正交相似化简

定理 任意 $n$ 阶实方阵 $\boldsymbol{A}$ 都正交相似于一个 $n$ 阶上 Hessenberg 实矩阵.

---

上 Hessenberg 实矩阵

$i>j+1$ 时，矩阵的元素 $a_{ij}=0$，其中 $i=1,...,n;j=1,...,n-1$，形如

$$\left[\begin{array}{cccccc} * & * & * & \cdots & * & *\\ * & * & * & \cdots & * & *\\ & * & * & \cdots & * & *\\ & & * & \ddots & \vdots & \vdots\\ & & & \ddots & * & *\\ & & & & * & *\\ \end{array}\right]$$

---

Hessenberg 矩阵的性质

• 上 Hessenberg 矩阵与上三角矩阵的乘积是上 Hessenberg 矩阵
• 若上 Hessenberg 矩阵矩阵的下次对角线上出现零元素，则可按此零元素所在位置将其分为两个子块，每个子块均为上 Hessenberg 矩阵，例如

$$\left[\begin{array}{rrr:rr} -1 & 2 & 3 & 1 & -1\\ 1 & -1 & 4 & -7 & 0\\ 0 & 1 & 2 & -1 & 2\\ \hdashline 0 & 0 & 0 & 1 & -1\\ 0 & 0 & 0 & 2 &3 \end{array}\right]$$

---

推论 实对阵矩阵正交相似于三对角线矩阵.

---

小结

• 欧式空间和酉空间
  
  • 内积、向量的长度
• 度量矩阵与正交化
  
  • Gram-Schimdt 正交化
  • 空间的正交补
• 正交变换、对称变换（酉变换、酉对称变换）
  
  • 正交矩阵、对称矩阵（酉矩阵、Hermite 矩阵）
• 旋转变换与 Householder 变换

---

正交投影变换

例 设 $W$ 是欧式空间 $V^n$ 的子空间，则对任意 $\boldsymbol{\xi}\in V^n$ ，有唯一分解：

$$\boldsymbol{\xi}=\boldsymbol{\alpha}+\boldsymbol{\beta}, \quad \boldsymbol{\alpha} \in W, \quad \boldsymbol{\beta} \in W^{\perp}$$

定义 $V^n$ 上的映射 $T$ ： $T\boldsymbol{\xi}=\boldsymbol{\alpha}$ .

(1) 证明 $T$ 是线性变换
(2) 设 $\boldsymbol{\xi}\in V^n$ ， $\boldsymbol{\xi}\notin W$ ，则 $|\boldsymbol{\xi}-T \boldsymbol{\xi}| \leq|\boldsymbol{\xi}-\boldsymbol{\gamma}|, \quad \forall \boldsymbol{\gamma} \in W$

---

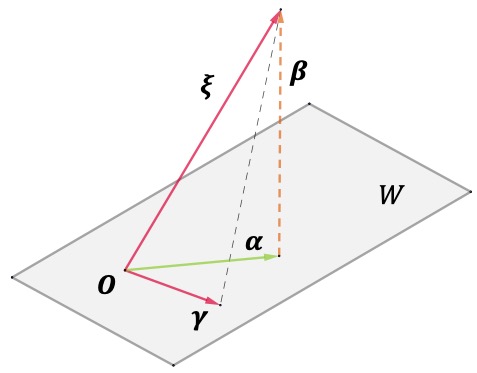
提示

• (1) 验证定义即可
• (2) 设 $\boldsymbol{\xi}\in V^n$ ， $\boldsymbol{\xi}\notin W$
  
  • $\boldsymbol{\xi}=\boldsymbol{\alpha}+\boldsymbol{\beta}, \quad \boldsymbol{\alpha} \in W, \quad \boldsymbol{\beta} \in W^{\perp}, \quad \boldsymbol{\beta} \neq\boldsymbol{0}$
• 对任意 $\boldsymbol{\gamma}\in W$ ， $\boldsymbol{\beta}\perp T\boldsymbol{\xi}-\boldsymbol{\gamma}$
• 由勾股定理
  
  • $|\boldsymbol{\xi}-\boldsymbol{\gamma}|^{2}=|\boldsymbol{\beta}+(T \boldsymbol{\xi}-\boldsymbol{\gamma})|^{2}$
    
    • $=|\boldsymbol{\beta}|^2+|(T \boldsymbol{\xi}-\boldsymbol{\gamma})|^{2}\geq|\boldsymbol{\beta}|^2=|\boldsymbol{\xi}-T\boldsymbol{\xi}|^2$

---

正交投影变换与投影矩阵

• 在标准正交基下，正交投影变换对应的矩阵称为投影矩阵.
• 注意到投影映射具有幂等性（$T^2=T$），容易验证其对应的矩阵也具有幂等性（$\boldsymbol{A}^2=\boldsymbol{A}$），因此也称为幂等矩阵（Idempotent Matrix）.
• 可以证明 (自行验证)
  
  • 幂等矩阵的特征值只能是 $0$ 或 $1$.
  • 如果 $\boldsymbol{A}$ 是幂等矩阵，则 $\boldsymbol{I}-\boldsymbol{A}$ 也是.

---

酉空间中的 Householder 变换

定理 设 $\boldsymbol{e} \in \mathbb{C}^{n}$ 是一给定的单位向量，则对任意的向量 $\boldsymbol{x} \in \mathbb{C}^{n}$ ，存在 $n$ 阶 Householder 矩阵 $\boldsymbol{H}$ ，使得

$$\boldsymbol{H}\boldsymbol{x}=a\boldsymbol{e}$$

其中 $a\in\mathbb{C}$ ，$|a|=|\boldsymbol{x}|$ 且 ${a} {\boldsymbol{x}}^{\mathrm{H}}{\boldsymbol{e}}\in\mathbb{R}$.

• 即：Householder变换（镜像变换）可以将任意一个向量正交变换到指定方向.

---

证明：

• 若 $\boldsymbol{x}=\boldsymbol{0}$ ，令 $a=0$ ，则对任意 Householder 矩阵 $\boldsymbol{H}$ ，都有 $\boldsymbol{Hx}=\boldsymbol{0}=0\boldsymbol{e}$.

• 考虑 $\boldsymbol{x}\ne\boldsymbol{0}$, 不妨设 $\boldsymbol{x}$ 与 $\boldsymbol{e}$ 线性无关（否则取 $\boldsymbol{H}=\boldsymbol{I}$）.

• 取 $a=\frac{\overline{\langle\boldsymbol{e},\boldsymbol{x}\rangle}}{|\langle\boldsymbol{e},\boldsymbol{x}\rangle|}|\boldsymbol{x}|\in\mathbb{C}$ ，则:

  • $|a|=|\boldsymbol{x}|$

  • $a\boldsymbol{x}^{\mathrm{H}}\boldsymbol{e}=a\langle\boldsymbol{e},\boldsymbol{x}\rangle=\frac{\overline{\langle\boldsymbol{e},\boldsymbol{x}\rangle}}{|\langle\boldsymbol{e},\boldsymbol{x}\rangle|}|\boldsymbol{x}|\langle\boldsymbol{e},\boldsymbol{x}\rangle=|\langle\boldsymbol{e},\boldsymbol{x}\rangle||\boldsymbol{x}|\in\mathbb{R}$

---

• 令 $\boldsymbol{\omega}=\frac{\boldsymbol{x}-a\boldsymbol{e}}{|\boldsymbol{x}-a \boldsymbol{e}|}$，$\boldsymbol{H}=\boldsymbol{I}-{2}\boldsymbol{\omega}{\boldsymbol{\omega}}^{\mathrm{H}}$.

• $\boldsymbol{H}\boldsymbol{x}=\left(\boldsymbol{I}-{2} {\boldsymbol{\omega}} {\boldsymbol{\omega}}^{\mathrm{H}}\right)\boldsymbol{x}=\boldsymbol{x}-2 \boldsymbol{\omega} \boldsymbol{\omega}^{\mathrm{H}}\boldsymbol{x}$

  • $=\boldsymbol{x}-2 \boldsymbol{\omega}^{\mathrm{H}}\boldsymbol{x}\boldsymbol{\omega}$

  • $=\boldsymbol{x}-2 \frac{(\boldsymbol{x}-a \boldsymbol{e})^{\mathrm{H}}}{|\boldsymbol{x}-a \boldsymbol{e}|} \boldsymbol{x}\frac{(\boldsymbol{x}-a \boldsymbol{e})}{|\boldsymbol{x}-a \boldsymbol{e}|}$

  • $=\boldsymbol{x}- \frac{2(\boldsymbol{x}-a \boldsymbol{e})^{\mathrm{H}} \boldsymbol{x}}{|\boldsymbol{x}-a \boldsymbol{e}|^{2}}(\boldsymbol{x}-a \boldsymbol{e})$.

---

以下证明 $\frac{2(\boldsymbol{x}-a \boldsymbol{e})^{\mathrm{H}} \boldsymbol{x}}{|\boldsymbol{x}-a \boldsymbol{e}|^{2}}=1$.

• 由 $\langle a\boldsymbol{e},\boldsymbol{x}\rangle=a\boldsymbol{x}^{\mathrm{H}}\boldsymbol{e}\in\mathbb{R}$, 故 $\langle \boldsymbol{x},a\boldsymbol{e}\rangle=\overline{\langle a\boldsymbol{e},\boldsymbol{x}\rangle}=\langle a\boldsymbol{e},\boldsymbol{x}\rangle$.
• $|\boldsymbol{x}-a \boldsymbol{e}|^{2}=\langle\boldsymbol{x}-a\boldsymbol{e},\boldsymbol{x}-a\boldsymbol{e}\rangle$
  
  • $=\langle\boldsymbol{x},\boldsymbol{x}\rangle-\langle\boldsymbol{x},a\boldsymbol{e}\rangle-\langle a\boldsymbol{e},\boldsymbol{x}\rangle+\langle a\boldsymbol{e},a\boldsymbol{e}\rangle$
  • $=\langle\boldsymbol{x},\boldsymbol{x}\rangle-2\langle \boldsymbol{x},a\boldsymbol{e}\rangle+|a|^2\langle \boldsymbol{e},\boldsymbol{e}\rangle$
  • $=2(\langle\boldsymbol{x},\boldsymbol{x}\rangle-\langle \boldsymbol{x},a\boldsymbol{e}\rangle)=2\langle \boldsymbol{x},\boldsymbol{x}-a\boldsymbol{e}\rangle$
  • $=2(\boldsymbol{x}-a\boldsymbol{e})^{\mathrm{H}}\boldsymbol{x}$.
• 综上 $\boldsymbol{H} \boldsymbol{x}=\boldsymbol{x}-(\boldsymbol{x}-a\boldsymbol{e})=a\boldsymbol{e}$.

---

例 给定单位向量 $\boldsymbol{e}=[1\;0\;0\;0]^{\mathrm{T}}$ ，对向量

$$\boldsymbol{x}_1=[0\;3\;0\;4]^{\mathrm{T}},\quad \boldsymbol{x}_2=[2\mathrm{i}\;\;0\;\;-\mathrm{i}\;\;2]^{\mathrm{T}}$$

分别求 Householder 矩阵 $\boldsymbol{H}_i$ ，使得

$$\boldsymbol{H}_i\boldsymbol{x}_i=a\boldsymbol{e}\quad(i=1,2) .$$

---

提示：

• 对 $\boldsymbol{x}_1=[0\;3\;0\;4]^{\mathrm{T}}$，令 $a_1=|\boldsymbol{x}_1|=5$.
• $\boldsymbol{\omega}_1=\frac{\boldsymbol{x}_1-a_1 \boldsymbol{e}}{|\boldsymbol{x}_1-a_1 \boldsymbol{e}|}=\frac{1}{5 \sqrt{2}}\left[\begin{array}{c}{-5} \\ {3} \\ {0} \\ {4}\end{array}\right]$.
• $\boldsymbol{H}_1=\boldsymbol{I}-2 \boldsymbol{\omega}_1 \boldsymbol{\omega}_1^{\mathrm{H}}=\frac{1}{25}\left[\begin{array}{cccc}{0} & {15} & {0} & {20} \\ {15} & {16} & {0} & {-12} \\ {0} & {0} & {25} & {0} \\ {20} & {-12} & {0} & {9}\end{array}\right]$.
• 于是 $\boldsymbol{H}_1 \boldsymbol{x}_1=5 \boldsymbol{e}=[5\;0\;0\;0]^{\mathrm{T}}$.

---

• 对 $\boldsymbol{x}_2=[2\mathrm{i}\;\;0\;\;-\mathrm{i}\;\;2]^{\mathrm{T}}$，$|\boldsymbol{x}_2|=3$ ， $\boldsymbol{x}_2^{\mathrm{H}} \boldsymbol{e}=-2\mathrm{i}$.
• 令 $a=3\mathrm{i}$.
• $\boldsymbol{\omega}_2=\frac{\boldsymbol{x}_2-a_2 \boldsymbol{e}}{|\boldsymbol{x}_2-a_2 \boldsymbol{e}|}=\frac{1}{\sqrt{6}}\left[\begin{array}{c}{-\mathrm{i}} \\ {0} \\ {-\mathrm{i}} \\ {2}\end{array}\right]$.
• $\boldsymbol{\omega}_2 \boldsymbol{\omega}_2^{\mathrm{H}}=\frac{1}{\sqrt{6}}\left[\begin{array}{c}{-\mathrm{i}} \\ {0} \\ {-\mathrm{i}} \\ {2}\end{array}\right] \frac{1}{\sqrt{6}}\left[\begin{array}{cccc}{\mathrm{i}} & {0} & {\mathrm{i}} & {2}\end{array}\right]=\frac{1}{6}\left[\begin{array}{cccc}{1} & {0} & {1} & {-2\mathrm{i}} \\ {0} & {0} & {0} & {0} \\ {1} & {0} & {1} & {-2\mathrm{i}} \\ {2\mathrm{i}} & {0} & {2\mathrm{i}} & {4}\end{array}\right]$

---

• 令 $\boldsymbol{H}_2=\boldsymbol{I}-2 \boldsymbol{\omega}_2 \boldsymbol{\omega}_2^{\mathrm{H}}=\frac{1}{3}\left[\begin{array}{rrrr}{2} & {0} & {-1} & {2\mathrm{i}} \\ {0} & {3} & {0} & {0} \\ {-1} & {0} & {2} & {2\mathrm{i}} \\ {-2\mathrm{i}} & {0} & {-2\mathrm{i}} & {-1}\end{array}\right]$.
• 则 $\boldsymbol{H}_2 \boldsymbol{x}_2=3\mathrm{i}\boldsymbol{e}=[3\mathrm{i}\;0\;0\;0]^{\mathrm{T}}$.