3.2 青岛正睿 Day3 博弈

正睿OI

[POI2009]KAM-Pebbles
PA 2009：https://www.lydsy.com/JudgeOnline/problem.php?id=2000
下面的某道类似的例题：https://www.cnblogs.com/SovietPower/p/9879090.html
不平等博弈 例题1：https://www.cnblogs.com/SovietPower/p/9851581.html
不平等博弈 例题2：TCO17 Final 450

图片挂了可以看这里。

某道题

$Description$
给定$n\times m$的网格，给定$(1,i),(i,1)$这些位置是胜还是负。在$(x,y)$位置有一个棋子，两人轮流向左或向上移动这个棋子，直到移到$(1,i)$或$(i,1)$。求谁能赢。
$Solution$
首先暴力算每个格子上的$SG$函数。打表发现，两行两列之后（从第三行第三列开始），每条对角线上的格子上的$SG$函数是相同的。所以暴力求出第二行第二列每个格子的$SG$函数即可。

AGC 002E.Candy Piles(博弈论)

$Description$
给定$n$堆糖，数量分别为$a_i$。Alice和Bob轮流操作。每次可以吃掉最多的一堆，也可以每堆各吃掉一个。无法操作的人输，求谁能赢。
$n\leq10^5,\ a_i\leq10^9$。
$Solution$

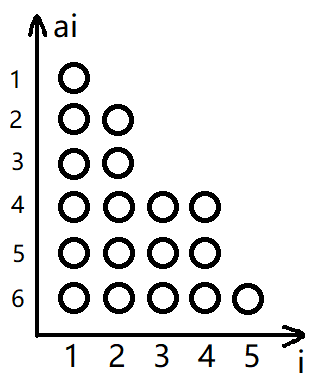
画这图累死了= = 虽然确实有点丑
假设有$5$堆糖，把它画成这样。我们发现每次操作就是拿掉最左边一列或最下边的一行。那么可以看成，初始在$(1,1)$，每次向右或向上走一步。
考虑求$SG$。边界位置的$SG$值显然为$0$，且$SG$只有$01$两种取值表示胜负。其余位置的$SG$都可以求出，但是复杂度会炸。
打表可以发现，除去最边上一层，同一条副对角线上的位置的$SG$值是相同的，即$sg(x,y)=sg(x+1,y+1)$。
考虑若$sg(x+1,y+1)=1$，$(x,y)$的后继的后继会有$(x+1,y+1)$这一必胜态，所以$sg(x,y)=1$；若$sg(x+1,y+1)=0$，则$(x,y)$的后继存在必败态的后继，所以$sg(x,y)=0$。
然后我们就可以找第一个满足$i+1>A_{i+1}$的位置$(i,i)$，求$(i,i)$的$SG$值，即右边上边各有多少个位置有糖即可。
这个结论是很常用的结论：同一条对角线上的$SG$值相同。
https://www.cnblogs.com/SovietPower/p/10473317.html

POJ.3922.A simple stone game(K倍减法游戏 博弈论)

$Description$
有$n$个石子，先手第一次可以取任意个，但不能一次全取完。之后每个人取的个数不能超过另一个人上次取的数量的$k$倍，不能取的人输。求先手是否有必胜策略。如果有，求先手第一次最少需要取多少个。
$Solution$
我竟然做过。。毫无印象，而且牛客提高集训是出了道原题= =。但是思路貌似和下面说的不太一样（本质是一样的吧），可以看这里的C题。

https://blog.csdn.net/ta201314/article/details/44892055
http://www.cnblogs.com/jianglangcaijin/archive/2012/12/19/2825539.html

上面两个都写的不错，我懒得写了。。
大体就是，$k=1$时，可以证明当且仅当石子数为$2^k$时先手必败；$k=2$时，是Fibonacci博弈，可以证明当且仅当是斐波那契数时先手必败。证明过程都类似。
推广到$k\geq3$，同样构造数列，令$A_i=A_{i-1}+A_k,\ A_{k-1}*K\lt A_{i-1}\leq A_k*K$，即令数列中相邻两项的比值不小于$K$。胜负就判断是否存在$A_i=n$即可。
然而$dls$说的是，暴力三方DP->单调性优化到平方->数据结构优化到线性...？但是毕竟还是$O(n)$的。。

五个$SG$函数的小练习

$Description$
1. 有一堆石子，两人轮流取，每次可以取$1\sim k$个，谁不能取谁输。求谁能赢。
2. 有一堆石子，两人轮流取，每次可以取$l\sim r$个，谁不能取谁输。求谁能赢。
3. 有$n$堆石子，两人轮流取，每次可以在一堆石子里选任意多的石头，或者把一堆石头分裂成两堆，谁不能操作谁输。求谁能赢。（$Lasker's\ Nim$）
4. $Nim$游戏，有一个数$n$，每次能拿掉当前数的一个因子（除去它本身，将当前数减掉这个因子）。
5. $Nim$游戏，每次能拿掉与当前数互质的一个数。
$Solution$
1. $SG(i)=i\%(1+k)$
2. $SG(i)=i\%(l+r)/l$
找到规律，再用归纳证明...
3. 一个游戏分裂成两个独立的游戏，$SG$值就是两个游戏的$SG$值异或起来：$SG(i)=\mathbb{mex}\{sg[j],sg[j]^{\wedge}sg[i-j]\}$。
然后打表能发现规律。见这道题。
4. 找规律发现是__builtin_ctz(n)（二进制后缀$0$的个数）。
5. 找规律。发现$SG(n)$是$n$最小质因数的编号。

某道题

$Description$
给定两个字符串$S,T$，$Alice$和$Bob$每次可以删掉$S$最前面或最后面的一个字符。若一个人操作后$S$变成了$T$的子串，该人输。求谁能赢。
$Solution$
我...我个zz忘了啊而且不会（好像没听..）。

CF某题

$Description$
有$1\sim n$共$n$个数字，两个人轮流选一个数字删除，如果$x$被删除了，那么$x^2,x^3,...$也会一起被删除。求谁能赢。
$n\leq10^9$。
$Solution$
我...我又忘了（当时好像也没听...）。

某题...

$Multi-SG$。见链接。

SPOJ COT3.Combat on a tree(博弈论 Trie合并)

$Description$
给定一棵$n$个点的树，每个点是黑色或白色。两个人轮流操作，每次可以选一个白色的点，将它到根节点路径上的所有点染黑。不能操作的人输，求先手是否能赢。如果能，输出第一步选择哪些节点能赢。
$n\leq10^5$。
$Solution$
Orz huzecong。

对于叶子节点，如果能染色，$SG(x)=1$，否则$=0$。
考虑从下往上算每棵子树的$SG$值。设$SG(x)$表示$x$子树的$SG$值，$g(x)$表示对$x$这棵子树操作能得到的后继的$SG$值集合（只考虑$x$子树），那么$SG(x)=\mathbb{mex}\{g(x)\}$。

考虑如何计算$g(x)$。令$sum[x]=sg(v_1)\ \mathbb{xor}\ sg(v_2)\ \mathbb{xor}...,\ v_i\in son[x]$。
若$x$是黑点，假设这次操作选了$v_i$子树中的某个点，那么其它子树状态不变，$v_i$子树的后继状态会变成$g(v_i)$中的某个，所以$g(x)=sum[x]\ \mathbb{xor}\ sg(v_i)\ \mathbb{xor}\ (g(v_i)中的某个值)$。
把子树内每个$g(v_i)$整体$\mathbb{xor}$一个数，合并起来，就可以得到$g(x)$了。
若$x$是白点，多了一种选$x$的后继，选$x$后得到状态的$SG$值就是$sum[x]$。所以在$g(x)$中再插入一个$sum[x]$即可。

还要支持求$\mathbb{mex}$，可以用$01Trie$维护。合并的时候可以启发式合并，$O(n\log^2n)$，也可以类似线段树合并做到$O(n\log n)$。

对于第二问，考虑选择一个节点后局面的$SG$值。容易发现就是除去它到根节点路径上的点的所有点的$SG$值的异或和。
记$up[x]$表示除去$x$到根节点路径上的点外，所有节点的$SG$值异或和，那么$up[x]=up[fa[x]]^{\wedge}sum[fa[x]]^{\wedge}SG(x)$。选择$x$后$x$的各棵子树是独立的，局面的$SG$值就是$up[x]^{\wedge}sum[x]$（$up$也可以直接$DFS$的时候传个参）。
所以如果$up[x]^{\wedge}sum[x]=0$，选这个点就是必胜的。

这个$SG$值的最大值是啥啊...
注意$Trie$要特判叶子的地方（尤其是Merge，注意像线段树合并一样判下叶子）（我怎么老是写错...）。
https://www.cnblogs.com/SovietPower/p/10555664.html

Project Euler 306(打表)

$Description$
$1\times n$的纸条，两人轮流操作，每次拿走相邻的两个，谁不能操作谁输。求$1\sim 10^6$中有多少个数做$n$能使得先手必胜。
$Solution$
打表，然后利用$txt$找循环节（前一两行没规律，后面是循环的）。

Goodbye 2018.H.New Year and the Tricolore Recreation(博弈论 bitset)

$Description$
Alice和Bob玩游戏。给定$n,f$，表示有$n$行的棋盘，每行有三个棋子。Alice每次可以选择一行将该行左边的一个或两个棋子往右移动$d$步，Bob每次可以选择一行将该行右边的一个或两个棋子往左移动$d$步。
要求移动时一个棋子不能跨越另一个棋子，且$d$是质数或两个质数的乘积，且$d\neq f$。求出Alice和Bob分别作为先手时，谁能赢。
$n\leq10^5,\ 坐标绝对值\leq10^5$。
$Solution$
右移一个棋子就是缩小第二三两个棋子之间的距离，右移两个棋子就是缩小一二两个棋子之间的距离。设三个棋子位置为$a,b,c$，每一行实际就是两个棋子数为$c-b-1,b-a-1$的$nim$游戏。
如果能算出棋子数为$x$的游戏的$SG$函数，将$2n$个游戏的$sg$值全异或起来即可。考虑如何算，显然有$sg(x)=\mathbb{mex}_{d\in P}\{sg(x-d)\}$，但是复杂度是$n^2$的。
打个表发现，$sg$值最大不会超过$100$（我也不知道怎么能得出的）。我们开$100$个$bitset\ A[i]$，分别表示每个数字是否存在$sg$值为$i$的后继。再预处理$d\in P$的$bitset\ S$。这样从小到大求$sg(i)$时，就for一遍看它不存在哪个$sg$值的后继；然后$A[sg(i)]|=S<<i$即可（更新上能到$i$的位置）。
复杂度$O(\frac{n^2}{w})$。
https://www.cnblogs.com/SovietPower/p/10209994.html

某道数据结构题（求区间mex）

$Description$
每个点$x$可以走到$[l_x,r_x]$中的某个点，求每个点的$SG$值。
$n\leq10^5$。
$Solution$
就是求区间$\mathbb{mex}$。见BZOJ3585。
先预处理出$1\sim i$区间的$\mathbb{mex}$，更新到线段树上。把询问按左端点排序。考虑从$[l,r]$到$[l+1,r]$时，若$nxt[A_l]>r$，则$[l+1,r]$中$\mathbb{mex}$大于$A_l$的全部会变成$A_l$。给$[l+1,nxt[A_l]-1]$这个区间取$\min$即可。询问就是单点查询。

N阶Nim

$Description$
$N$阶Nim游戏：有$k$堆石子，每堆各有$x_1,x_2,...,x_k$个石子。双方轮流操作，每次可以选$1\sim N$堆石子，从选出的每堆中取走任意个（可以全取完）。取走最后一个石子的人赢。求谁能赢。
$Solution$
结论：当且仅当$x_1,x_2,...,x_k$在二进制表示下的每一位上，$1$的个数和是$N+1$的倍数时，先手必败。否则先手必胜。
证明见这里。

三人Nim游戏

$Description$
有$n$堆石头，三个人玩$Nim$。拿走最后一个的是第一名，倒数第二个拿的是第二名，另一个是第三名。每个人都想使自己的名次最高，求最终三人的名次。
$Solution$
结论：最后一个人必胜，当且仅当把所有数字用二进制表示后，每一位上的数加起来模$3$等于$0$（类似普通$Nim$的异或和）。
判断第一个人是否必胜就可以直接判断能否走到必胜态。
否则就是第二个人赢。
分析比较复杂...我又忘了...

阶梯Nim

$Description$
有$n$堆石子，两个人轮流取。每次可以在第$i$堆中拿若干堆石头放到第$i-1$堆中（$i\geq1$），无法操作的人输。求谁能赢。
$Solution$
把奇数堆石子拿出来做$Nim$游戏，先手必败当且仅当奇数堆石子数异或和为$0$。
因为如果一个人操作偶数堆，另一个人可以将他移动的石子放到下一个偶数堆里去，不影响奇数堆的状态。然后讨论一下就可以得出这个结论了。
一个变形。

翻硬币游戏

$Description$
$n$枚硬币排成一排，有的正面朝上，有的反面朝上。从左到右给硬币进行编号$1...n$。
游戏者根据某些约束反硬币（如：每次只能翻$1$或$2$枚，或者每次只能翻连续的几枚），但他所翻动的硬币中，最右边的必须是从正面翻到反面。谁不能翻谁输。
$Solution$
有个结论：局面的$SG$值为局面中每个正面朝上的棋子单一存在时的$SG$值的异或和。如：SG[0100101]=SG[01]^SG[00001]^SG[0000001]。其中$1$表示正面朝上。（这样就只需要计算有$n$个棋子，只有最后一个是$1$的$SG$值，打表找规律）
连续翻任意个的游戏的$SG$函数，假设局面共$n$个棋子，最右边为正其余为反，那么由上面的结论可以得到$SG(n)=\mathbb{mex}\{SG(0),SG(n-1),SG(n-1)^{\wedge}SG(n-2),...,SG(n-1)^{\wedge}...SG(1)\}$。
具体的见链接吧，很全。不想写了。

CF.494E.Sharti

$Solution$
不想看。最后是个求矩形并。

树上翻硬币

$Description$
给定一棵$n$个节点的有根树，每个节点上有一个硬币。每次可以选择一个正面朝上的硬币，将它以及在它的所有后代中选一个子集翻转。不能操作的人输。求谁能赢。
$Solution$
课件：

每个硬币是独立的，证明见上。
只需要求出每个点的$SG$即可。
通过归纳可得，每个点的$SG$值为$2^{到最深叶子的距离}$。

树上删边游戏

结论：叶节点的$SG$值为$0$，非叶节点的$SG$值为，它所有子节点$SG$值加$1$后的异或和。
具体见链接。

Anti-SG

$Description$
$Anti-SG$游戏：决策集合为空（局面中所有单一游戏的$SG$值为$0$）的游戏者赢，其余规则与$SG$游戏相同。
$Solution$
$SJ$定理：
对于$Anti-SG$游戏，如果我们规定当局面中所有单一游戏的$SG$值为$0$时，游戏结束，则先手必胜当且仅当：
1. 游戏的$SG$函数不为$0$且游戏中某个单一游戏的$SG$函数值大于$1$
2. 游戏的$SG$函数为$0$且没有某个单一游戏的$SG$函数值大于$1$

BZOJ.1115.[POI2009]石子游戏Kam(阶梯博弈)

$Description$
有$n$堆石子。除了第一堆外，每堆石子个数都不少于前一堆的石子个数。两人轮流操作，每次可以从一堆石子中拿掉任意多的石子，但要保证操作后仍然满足初始时的条件。谁没有石子可拿时输。求先手是否必胜。
$Solution$
限制条件就是相邻两个数的差非负。那么记查分数组$d_i=a_i-a_{i-1}$。假设拿走第$i$堆的$x$个石子，影响是$d_i$-=$x$，$d_{i+1}$+=$x$，就相当于从$d_i$中拿$x$个给$d_{i+1}$。
显然原题意和对差分数组做反向的阶梯$Nim$是等价的，然后就做完啦。
https://www.cnblogs.com/SovietPower/p/10555645.html

CF.388C.Fox and Card Game(博弈)

$Description$
有若干排石子，每一排又有若干堆石子。$Alice$每次可以选择一排，取走这排最左边的一堆石子；$Bob$每次可以选择一排，取走这排最右边的一堆石子。两个人都想最大化自己的石子数目，$Alice$先手，求最后两人各有多少石子。
$Solution$
对于一排石子，假设有偶数堆，那么两人会各拿一半。因为$Alice$能保证自己得分$\geq$左边一半的和，$Bob$能保证自己得分$\geq$右边一半的和。（脑补一下好了）
如果是奇数，先手（先操作这一堆的人）可以取到最中间的石子。把所有奇数堆的排的中间那堆拿出来，排个序，两人一定会轮流从大到小取。

BZOJ.2000.[HNOI2010]stone取石头游戏(博弈)

$Description$
有一些数字，被分成若干双端队列（从两边都可以取）和最多两个栈（只能从某一边一个一个取）的形式。两人轮流取这些数字，每个人都想最大化自己取到的数字和，求最后两人各能取到多少。
$n\leq10^6$。
$Solution$
对于最左边的栈，如果有$A_1\geq A_2$，那么先手取了$A_2$，后手一定会取走$A_1$（如果赚，显然后手要取；如果不赚，先手可以取别的最后依旧让后手取走）。同样扩展到左边连续递减的一段，两人都是轮流取的（这样$i$为奇数时，后手取$A_{i-1}$可能就不赚了）。
最右边的栈同理。
然后能发现，谁能取到最左和最右边的数只与数字总个数有关，如果一共奇数个，先手可以同时取走最左和最右，否则后手可以。（nb...感觉真要证会很复杂）
那么我们就可以处理完左右递减的那一段了。剩下的等会再说。

考虑双端队列，如果有$A_{i-1}\leq A_i\geq A_{i+1}$，且先手取走$A_{i-1}$，那么后手一定去取$A_i$，先手一定会取走$A_{i+1}$，所以收益差是固定的，为$A_i-A_{i-1}-A_{i+1}$。这里的先手是指取$A_{i-1}$的人。那么我们就可以将这三个数压成一个数，去求收益差。
那么我们就可以将这种上凸的情况全合并掉，把序列变成只有递减的、递增的、下凸的三种情况，显然这三种一定是从大到小轮流选的。

这样合并两个栈，因为左边递减的已经合并了，也没有上凸情况了，所以只剩下递增情况了。同样和双端队列那些放一起轮流选就行了。

最后求出个差，知道总数就知道答案了。

注意合并后的元素是可能出现$0$的，空位置要再开个数组判。
https://www.cnblogs.com/SovietPower/p/10566210.html

PS:
后面都懒得看咯（也没时间搞这个了）。
还剩下几道（或者十几）题以及$surreal\ number$。如果不退役还会来补哒。

Nim积

$Nim$积有结合律、交换律，对$Nim$和$xor$有分配律。
咕咕了。

小练习 矩形翻硬币

$Description$
翻硬币，可以翻转以这个点为右下角的矩形。
$Solution$
不知道。

Project Euler 459

$Description$
咕咕。
$Solution$
求出每行每列单独的$SG$值，然后乘一下。

$Description$

$Solution$

$Description$

$Solution$

$Description$

$Solution$

$Description$

$Solution$

$Description$

$Solution$