3.2 青岛正睿 Day1 构造

正睿OI

---

---

URAL 1979 Resources Distribution(构造)

$Description$
给定$n$。你需要对一个$n\times n\times n$的立方体，在外表面的$6n^2$个面上写上$1\sim 6n^2$这些数字，使得从任意格子出发向任意一个方向走一圈和都相等。
$n\leq100$。
$Solution$
考虑一个面和其对面同样位置的面，一定会同时出现在某个环中。
所以令任意两个相对的面的和相同。设成$i$和$6n^2+1-i$就好了。

---

CF.226D.The table(构造)

$Description$
给定一个$n\times m$的矩阵$A_{i,j}$，每次可以将一列或一行取负。求一个方案使得若干次操作后，每行每列的和都非负。
$n,m\leq100,\ 元素绝对值|A_{i,j}|\leq100$。
$Solution$
容易想到每次找和为负的一行或一列取负。这样做正确性及复杂度会有啥问题么？
注意到每次取负，所有数的和是单调递增的，所以一定会结束。且每次和至少会增加$2$（$-1\to1$），而所有数的和最小是$-10^6$，最大是$10^6$，所以最多操作$10^6$次，复杂度$O(10^6n)$。
自己写了写，写的真是麻烦。。不需要queue，每次$O(nm)$for一遍反转行列即可。
https://www.cnblogs.com/SovietPower/p/10462907.html

---

Andrew Stankevich Contest 44 (ASC 44) H.Huffman Codes

$Description$
给出$n$个哈夫曼编码的$0/1$个数$u_i,v_i$，问是否存在可能的哈夫曼编码（满足这$n$个数）。
$n\leq100,\ 0\lt u_i+v_i\leq100$。
$Solution$
首先$u_i+v_i$相同的肯定在同一深度，且同一深度一对$0$比另一个数多$1$，$1$比另一个数少$1$的两个数一定匹配，把它们合并即可。这样一直下去直到构造完成或出现矛盾。

---

CF.209C.Trails and Glades(构造 欧拉回路)

$Description$
给定一张$n$个点$m$条边的无向图，允许有自环重边。求最少加多少条边后，其存在从$1$出发最后回到$1$的欧拉回路。
注意，欧拉回路是指要经过所有边，无边（边包括自环）连向的孤立点不需要考虑。但是$1$一定要经过。
$n,m\leq10^6$。
$Solution$
如果图连通，奇度数点两两连边即可。
如果图不连通，对于每个奇度数点需要向外连一条边；没有奇度数点的连通块就随便找一个点往外连两条边。另外强制选$1$即可。
答案是统计的边数除以$2$。
https://www.cnblogs.com/SovietPower/p/10463381.html

---

ZOJ.3823.Excavator Contest(构造)

$Description$
在$n\times n$的网格上，由边界的某个格子出发四连通地经过所有格子恰好一次再回到边界上，要求拐弯的数量至少有$n\times(n-1)-1$次。
$n\leq512$。
$Solution$
嗯...在边界各种绕然后变成规模更小的问题？

---

Latvia U Contest 14 G.Mosaic(构造)

$Description$
有三种颜色的珠子各$a,b,c\leq2^{31}$个。求给出方案铺满若干层的正三角形，且三角形的每层颜色必须相同。
$Solution$
首先$a+b+c$必须是三角形数，否则无解。设$a+b+c=\frac{n(n+1)}{2},\ a<b<c$，即有$n$层。
关于方案构造，第一想法是贪心，每次把最多的放到最下一层去，但显然有反例。尝试做一些修正。
首先可以特判如果存在两个$1$或两个$2$无解。
$n\leq3$时，合法方案有哪些很好判。
$n>3$时，由$a+b+c=\frac{n(n+1)}{2}\gt3(n-1)$，可知$a\geq n$。
考虑枚举每一层$n$，若$n>b$，则放$a$；否则称这一层为可选择的，先放$a$。
这样我们能放到$n\leq 3$。因为$a+b+c=3$或$6$，所以此时不合法的情况只有$1\ 1\ 1$和$2\ 2\ 2$。
若之前存在可选择的层，那么找到最小的可选择层$k$，$k$和$k-1$颜色必然不同，且交换这两层后仍然合法，状态变成$0\ 1\ 2$或$1\ 2\ 3$。这样就$OK$了。
所以除去存在两个$1$或两个$2$的情况，只要$a+b+c$是三角形数，就一定存在合法方案。

---

NEERC2013 K.Kids in a Friendly Class(Erdős–Gallai定理)

$Description$
一张图有黑点和白点，每个黑点有$a$条边与黑点相连、$b$条边与白点相连；每个白点有$c$条边与黑点相连、$d$条边与白点相连。给出$a,b,c,d$，构造一张满足条件的图使得总点数最少。
$a,b,c,d\leq50$。
$Solution$
枚举黑点点数$n$，那么白点有$\frac{bn}{c}$个，黑点白点之间的边可以瞎连，很简单。
对于同色点，问题就是如何连边使得每个点的度数相等。
每次选剩余度数最大的两个点连显然是错的（比如$n=6,dgr=2$）。
每次找一个剩余度数最大的点，向剩余度数次大的若干点连，就OK了。
其实就是Havel–Hakimi算法或者Erdős–Gallai定理。这种方法可用于构造任意给定每个点度数的图。
范围这么小...怎么写都行了。
而且貌似不需要枚举$n$...可以算出来具体的$n$。在这里有代码，懒得看.jpg。

---

Udmurt SU + Izhevsk STU contest J. Cranes(思路 贪心)

$Description$
给定$n,m,k$。你需要把$n$个箱子从$0$移动到$m$。你可以用$k$个机械手，每个机械手同一时刻只能拿一个箱子，可以在一单位时间内向左或向右移动一格，或者不动，机械手提起/放下箱子的时间忽略不计。求将$n$个箱子全部移到$m$的最短时间。
$n,m,k\leq10^6$。
$Solution$
手算一个数据体会一下... $k=3,n=4,m=5$。
$Ans=10,11,12,13,15,20...$都能算出来...答案是$9$。
一种方案（不唯一）：
机械手$A$：把一个送到$5$，回到$3$再拿一个；
机械手$B$：把一个送到$3$，再回到$1$拿一个；
机械手$C$：把一个送到$1$，再回到$0$拿一个。

首先假设机械手数量小于等于箱子数量。每秒对机械手采取这样的贪心操作（先考虑离$m$较近的机械手）：
1. 如果有箱子在自己后面且没有被抓着，扔下手中的箱子往回走一步。
2. 否则当前位置一定有没被抓着的箱子，抓起它向前一步。
证明：这样可以使得所有手往回走的步数最少。

然而我好像还不会线性做法...貌似可以推个式子。

---

Ufa SATU + Bucharest U Contest J. Reverse Sort(归并排序)

$Description$
给定一个长为$n$的序列，每次可以反转一段区间，代价是区间长度。在总代价不超过$6\times10^4$的条件下将该序列排好序。
$n\leq3.2\times10^4$。
$Solution$
就是这道题，那里写的更详细。
假设值域只有$0/1$，可以从小区间到大区间归并排序，代价/复杂度是$O(n\log n)$的（$01$归并还有$0.5$的常数）。
扩展到一般情况。每次取一个$mid$，$\leq mid$的数设成$0$，$>mid$的数设成$1$，每次可以区分两堆数。那么复杂度是$O(0.5n\log^2n)$的。

另外有一种贪心，就是每次交换相邻的两段$01$，比如：10101010->01010101->00101011...。直接这样复杂度是$n^2$的。
考虑仍是每次交换相邻的两段$01$，但间隔一段$01$：10101010->01100110->00011110->00001111。可以发现开头$0$的个数呈几何增长（我没发现），所以复杂度$O(n\log n)$。但是应该比上面那个难写...但是这个思想应该（可能）很常用。

---

Andrew Stankevich Contest 42 C.Comparator Networks(构造)

$Description$
一个比较器$(i,j),\ i<j$会比较$i$和$j$这两个位置的比特$b_i,b_j$，若$b_i>b_j$则将$b_i,b_j$交换。
一个比较器网络是一系列依次执行的设定好参数的比较器。
一个比较器网络对某个比特序列（即一个$01$序列）是排序的，当且仅当输入这个比特序列的输出是单调递增的。
构造一个比较器网络（比较器数量$\leq1000$），使其对于给定的长为$n$的$01$序列$(n\leq10)$是非排序的，且对其他的所有$01$序列都是排序的。无解输出-1。
$Solution$
如果输入序列已经排好序显然无解。否则最前面那个$1$一定在最后面那个$0$前面。
令最后一个$0$的位置是$p_0$，固定$p_0$，把除$p_0$外的任意一对位置放一个比较器，即把其它所有位置排好序。
然后令当前第一个$1$的位置是$p_1$，固定$p_1$，把除$p_1$外的所有位置排好序。
这样对于初始序列，$p_1$位置上的$1$一定在最后面那个$0$的前面，所以是非排序的。
而对于其它任意序列，按$0$的个数和给定序列$0$的个数的大小关系分类讨论，可以发现是能排序的。

---

CodeChef Dec 14.Divide or die

$Description$
给出平面上一个的$n$度角（给三点坐标，$n$是整数）。求一个方案通过尺规作图将其$n$等分。无解输出$-1$。
$Solution$
我粘ppt了...

世界人民熟知不能三等分任意角...？
由大数学知，尺规扩张是最多是二次扩张。而三等分$60$度角需求解的多项式是三次的，故$60$度不可三等分。

考虑尺规直接画能画出什么度数的角。

$1$度/$2$度与$60$度不可三等分矛盾（否则就可以画出$20$度角了）。
若$3$度角可以画出，利用角度的加减法，任何不是$3$的倍数的整数度角都可以被等分，而所有$3$的倍数的角由于可被直接画出必然不能被等分（要利用给定角的两条射线画图）。

考虑怎么画$3$度角。
利用黄金分割三角形$72$度底角！$\sin72^{\circ}=(\sqrt{5}-1)/4$。
$\sqrt{5}$可通过直角边长为$2:1$的直角三角形得到。
$72$度四等分得到$18$度，等边三角形$60$度四等分得到$15$度，相减得到$3$度角。

---

World Finals 2014 A.Baggage

$Description$
初始序列为$BABABA...BA$（长度为$2n\leq200$）.每次可以移动相邻的恰好两个元素到某两个连续空位，求一个方案在最少次数内将其排为$AA...A若干空格BB...B$。序列的最左最右边算有无穷多个空位。
$Solution$
（如果能）最好还是先打个表看看规律...
看图...

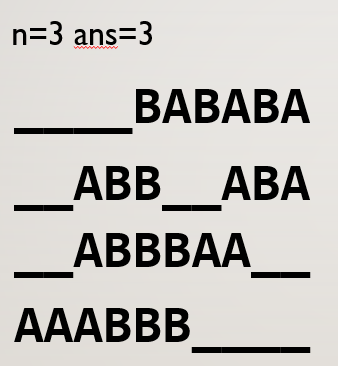
貌似出现$n=3$的时候比较特殊，可能要判一下...

---

CF.468C.Hack it!(构造)

$Description$
令$f(x)$表示整数$x$在十进制下各个数位的数字之和。给定$a$，求两个整数$l,r$，使得$\sum_{i=l}^rf(i)\equiv0\ (\mathbb{mod}\ a)$。
$1\leq a\leq10^{18},\ 1\leq l\leq r\leq10^{200}$，保证存在解。
$Solution$
考虑一个简单的性质：$f(x+10^y)=f(x)+1,\ x\lt10^y$。
不妨令$INF=10^{18}$，设$\sum\limits_{i=0}^{INF-1}f(i)\equiv p\ (\mathbb{mod}\ a)$。
由上面的性质可知，$\sum\limits_{i=1}^{INF}f(i)=p-f(0)+f(INF)=p+1$。
同理还有：$\sum\limits_{i=2}^{INF+1}f(i)=p+2...\ \sum\limits_{i=k}^{INF+k-1}f(i)=p+k$（都是模$a$意义下）。
然后就可以构造出$a=p+a-p=\sum\limits_{i=a-p}^{INF+a-p-1}f(i)$。所以令$l=a-p,\ r=10^{18}+a-p-1$就可以啦。
有个问题是求$\sum_{i=0}^{10^{18}-1}f(i)\ \mathbb{mod}\ a$。展开一下：

$$\begin{aligned}\sum_{i=0}^{10^{18}-1}f(i)&=(1+2+...+9)10^{17}+10\times\sum_{i=0}^{10^{17}-1}f(i)\\&=45\times10^{17}+10(45\times10^{16}+10\times\sum_{i=0}^{10^{15}-1}f(i))\\&=...\\&=18\times45\times10^{17}=81\times10^{18}\end{aligned}$$

这样就做完啦。

还有个做法是，考虑有$\sum\limits_{i=1+x}^{10^y+x}f(i)-\sum\limits_{i=1}^{10^y}f(i)=x,\ x\lt10^y$。枚举$y$，如果有$a-\sum\limits_{i=0}^{10^y}<10^y$，令$x$等于这个数，就有$\sum\limits_{i=1+x}^{10^y+x}f(i)=\sum\limits_{i=0}^{10^y}+a-\sum\limits_{i=0}^{10^y}=a$了。
需要预处理一下$\sum_{i=1}^{10^y}f(i)$，因为是上限$10$的幂所以算一下每个数出现次数即可（或者像上面一样直接算）。
https://www.cnblogs.com/SovietPower/p/10517540.html

---

CF.487C.Prefix Product Sequence(构造)

$Description$
对于一个序列$a_i$，定义其前缀积序列为$a_1\ \mathbb{mod}\ n,\ (a_1a_2)\ \mathbb{mod}\ n,...,(a_1a_2...a_n)\ \mathbb{mod}\ n$。
给定$n$，求一个$n$的排列，使得该排列的前缀积序列是$[0,1,2,...,n-1]$的一个排列。无解输出$NO$。
$n\leq10^5$。
$Solution$
考虑无解的情况。因为$n!\equiv0\ (\mathbb{mod}\ n)$，所以$(n-1)\not\equiv0\ (\mathbb{mod}\ n)$。
$n$为质数显然可以满足。否则设$n=pq$。
若$p\neq q$，那么有$(n-1)!\equiv0\ (\mathbb{mod}\ n)$，GG了。
若$p=q$，当$n>4$时，$2p<n$，所以也有$(n-1)!\equiv0\ (\mathbb{mod}\ n)$，GG。
所以$n$为大于$4$的合数时无解。特判一下$n=4$。

首先$a_1$要填$1$，$a_n$要填$n$。
考虑能不能直接让前缀积序列变成$1,2,...,0$。那么$a_i=\frac{i}{i-1}\ \mathbb{mod}\ n,\ i>1$。
只需要判断是否有$\frac{a}{a-1}=\frac{b}{b-1},\ 1\lt a\neq b\lt n$。
稍微化一下，$\frac{a}{a-1}=1+\frac1a,\ \frac{b}{b-1}=1+\frac1b$，而我们知道每个数的逆元是唯一的，所以这么做就OK啦。
https://www.cnblogs.com/SovietPower/p/10518469.html

---

CF.618F.Double Knapsack(构造 鸽巢原理)

$Description$
给定两个大小为$n$的可重集合$A,B$，集合中的元素都在$[1,n]$内。你需要从这两个集合中各选一个非空子集，使它们的和相等。输出方案。
$n\leq10^6$。
$Solution$
求子集是假的...对两个集合按任意顺序求个前缀和，记为$SA_i,SB_i$。不妨假设$SA_n\leq SB_n$。
那么能发现，对于每个$SA_i\ (0\leq i\leq n)$，找出最大的$SB_j\leq SA_i$的$j$，$SA_i-SB_j$的取值范围是$[0,n-1]$（如果$\geq n$则可以移动$j$），只有$n$种。而$i$的取值有$n+1$种。由鸽巢原理，那么一定存在一对$i,i'\ (i\neq i')$，使得$SA_i-SB_j=SA_{i'}-SB_{j'}$。因为元素大于$0$，所以$j\neq j'$。
那么有$SA_i-SA_{i'}=SB_j-SB_{j'}$，就可以得到答案啦。
https://www.cnblogs.com/SovietPower/p/10519255.html

---

ONTAK2014 SUM(构造)

题面：https://sio2.mimuw.edu.pl/c/wiekuisty_ontak2014/p/sum/
备份：链接: https://pan.baidu.com/s/1Nt3mZUXJpcG_S80i2ky_7w。提取码: nx2d。

$Description$
给定一个大小为$n$的正整数集$A$。你要求一个大小不超过$n$的集合$B$，满足$A$中每个元素都是$B$中某个子集的和，且$B$中所有子集的和两两不同。$B$中每个元素的大小不超过$10^{17}$。
$n\leq21,\ 1\leq A_i\leq 10^{17}$。
$Solution$
考虑将问题缩减到更小规模的方法。
设当前$A$集合中最小的奇数为$k$，将$A$中所有的奇数减去$k$，然后将$k$从集合中删掉。
剩下的数都是偶数，将它们除以$2$后去重，递归下去。
当递归到集合为空时，开始递归回去。
递归回去时每次把$B$中所有元素乘$2$，如果这层删掉过奇数$k$，就在$B$中加入$k$。

考虑这样的过程为什么能满足条件。
每次向$B$中加入的元素都是$A$中的元素，且$A$中删掉的元素一定会被加入到$B$，所以满足第一个条件。
模拟递归回去的过程来证明第二个条件。
当递归到最后时，空集满足条件二。
那么递归回来时$B$是满足条件二的，那么将$B$中每个元素乘$2$，仍满足条件，且此时$B$中全是偶数。
若这一层加进去了奇数$k$，那么新产生的子集和都是奇数，和之前全是偶数的子集和一定不相同。之前的子集和互不相同那么新产生的子集和也互不相同。那么$B$依旧是满足条件的。

---

CF.578E.Walking(构造)

$Description$
给定一个长为$n$的足迹序列（只包含$L,R$两种字符），你需要$LRLRLR...$这样交替在$L$和$R$上走（第一步可以选择$L$也可以选$R$）。当你在$L$时，下一步可以走到任意一个没走过的$R$；在$R$时，下一步可以走到任意一个没走过的$L$。求走完这个$L,R$序列最少需要往回走几次，并输出方案（往回走是指从位置$i$走到位置$j$，$j\lt i$）。保证存在一组可行方案。
$n\leq10^5$。
$Solution$
首先$L,R$数量差大于$1$无解。
如果我们需要往回走$k$次，那么我们可以将序列分成$k+1$个分别合法的子序列。
反过来，如果我们能将序列分成$k$个合法的子序列，小于往回走的次数是不是一定小于$k$？
考虑能否证明。我们将序列分成$LL,RR,LR,RL$四种合法的子序列（第一个字符表示序列开始是什么，第二个字符表示序列末尾是什么，因为只需要关心首尾字符），假设四种子序列分别有$a,b,c,d$个。首先有$|a-b|\leq1$。
然后我们可以用不超过$a+b-1$步将所有$LL,RR$合并成一个序列，这个序列可能是四种中的任意一种。
还可以用不超过$c-1$步将所有$LR$合并成一个$LR$。对$RL$同理。这样我们就得到了一个$LR$和一个$RL$子序列。
如果把其中一个子序列的最后一个字符给另一个，就可以变成一个$LL$和一个$RR$，且不会增加次数。
那么不论刚开始$LL,RR$合并出的子序列是哪种，都可以用不超过两步拼接上剩下的两个子序列。
这样最多使用$a+b-1+c-1+d-1+2=k-1$步。这样就证明了，如果我们能能将序列划分成$k$个合法子序列，一定可以构造方案使得最多往回走$k-1$次。（可是我还是觉得有点迷...）

现在的问题是怎么讲序列划分成尽量少的合法子序列。
我们发现可以跑最小路径覆盖（每个$L/R$向它后面所有$R/L$连边，$n-最大匹配数$就是答案）（图在官方题解里有）。
但还可以发现这个匹配实际上可以直接贪心，每个字符选它能匹配的点中最靠前的匹配即可。因为一定可以调整最大匹配使得满足这种贪心。
那么复杂度就是$O(n)$的了。
具体做的时候，可以拿个栈模拟一下拼接...（菜到不会写.jpg）
https://www.cnblogs.com/SovietPower/p/10523753.html

---

CF.472F.Design Tutorial: Change the Goal(构造 线性基 高斯消元)

$Description$
给定两个长为$n$的数组$x_i,y_i$。每次你可以选定$i,j$，令$x_i=x_i\ \mathbb{xor}\ x_j$（$i,j$可以相等）。要求若干次操作后使得$x$变成$y$，输出方案。操作次数不能多于$10^6$，无解输出$-1$。
$n\leq10^4,\ 0\leq x_i,y_i\leq10^9$。
$Solution$
考虑异或的两个基本性质：
1. 异或是可逆的，逆运算就是它本身。
2. 可以交换两个数：a^=b,b^=a,a^=b。

考虑线性基。构造出$x$的线性基，如果$y$中存在元素不能被$x$表示出来，那么无解。
我们发现对于不在线性基中的元素$x_i$，得到$y_i$是很容易的，只需要求一下在线性基中$\mathbb{xor}$出$y_i$需要异或哪些数。
对于在线性基中的元素，设有$t$个，它们之间不是很好做。把$t$个$x_i$对应的$y_i$需要$\mathbb{xor}$哪些基写成一个$t$位二进制数。由第二个性质，我们可以高斯消元将这个$t\times t$的矩阵消成一个上三角矩阵，这样从高位到低位做不同基之间就互不影响了，我们可以$\mathbb{xor}$出这个矩阵。
而由第一个性质，将高斯消元的过程反过来操作这个上三角矩阵，就可以还原回$y$数组。
https://www.cnblogs.com/SovietPower/p/10528796.html

---

CF.612E.Square Root of Permutation(构造)

$Description$
给定一个$n$的排列$p_i$，求一个排列$q_i$，使得对于任意$1\leq i\leq n$，$q_{q_i}=p_i$。无解输出$-1$。
$1\leq n\leq10^6$。
$Solution$
对排列$q_i$我们建一张图，边为$i\to q_i$。显然这张图是由几个环构成。
发现对于$q_{q_i}$的图，原来$q_i$中的奇环它们还是那样一个奇环，原来偶环的会分裂成两个大小相等的偶环。
所以对$p_i$建图，找出里面的环，是奇环就把相邻点间隔为$2$地插入到环里，是偶环就找到和它一样大的一个合并，找不到就无解。这样就可以得到$q_i$的图了。（每个偶环只能合并一次→_→）
复杂度$O(n)$。
https://www.cnblogs.com/SovietPower/p/10528010.html

---

一个正$n$边形...然而不知道题目名称是啥，$Scape$说的课件修正版咕咕了。

---

CF.715D.Create a Maze(构造)

$Description$
给定$n,m$。在$n\times m$的每次可以从$(x,y)$走到$(x+1,y)$或$(x,y+1)$。现在你需要在图中删去若干条边，使得从$(1,1)$走到$(n,m)$的方案数为$T$。删边是指，可以使某个$(x,y)$不能走到$(x+1,y)$或$(x,y+1)$。
如图：
$n,m\leq300,\ T\leq10^{18}$，删去的边数不能超过$300$。
$Solution$
容易发现如果以$x$的方案数进入某个格子，我们可以花$4$的代价将它隔成$2\times2$的方块，出去时的方案数就是$2x$。
所以可以考虑二进制分解。至于$+1$的实现，就可以从最上面引一条路径到对应位置去。
但是由于限制比较紧，二进制分解是不够的。
考虑用$3\times3$的方块构造。那么就是个$6$进制，我们需要能$+1,+2,...,+5$。

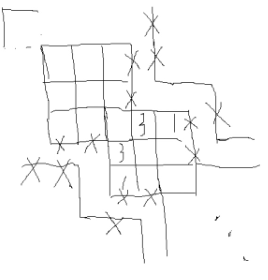
如图，如果我们保留右边第$4$列的横边，可以令方案数$+3$；保留第$5$列的横边，可以令方案数$+1$，这两个互不影响。左边的两条竖边同理。这样我们用一个类似引水渠(?)的构造就可以实现$+1$到$+5$了。

---

CF.566E.Restoring Map(构造)

$Description$
对于一棵树，定义某个点的邻居集合为所有距离它不超过$2$的点的集合（包括它自己）。
给定$n$及$n$个点的邻居集合，要求构造一棵$n$个点的树，使得每个给定的集合都对应一个点。输入保证有解。
$n\leq1000$。
$Solution$
如果两个点的邻居集合大小为$2$，那么交集中的两个点之间一定有边。这样我们就可以$O(\frac{n^3}{w})$确定出非叶节点以及它们之间的连边。
然后考虑叶节点应该挂到哪里。如果一个叶节点的邻居集合，和距离某个非叶节点不超过$1$的点的集合相同，那么这两个点之间有边。对于叶子$x$，所有包含$x$的邻居集合中最小的一定就是$x$的邻居集合。一个点数$\geq3$的树，离某个点距离不超过$1$的点的集合是互不相同的。
需要特判非叶节点只有一个和两个的情况。

官方题解是，找出叶子$x$的邻居集合，如果除去$x$集合大小$\geq3$，那么在集合内度数$>1$的点就是与$x$相邻的。否则集合大小是$2$，这种情况有些难判，但是与$x$相邻的点一定只与一个非叶节点相连。所以我们只需要特判$x-a-b-...$这种情况。
还有种并查集的写法，太傻逼了看不懂了QAQ。
https://www.cnblogs.com/SovietPower/p/10531749.html

---

Special Tour(Asia Hong Kong Regional Contest 2016)

$Description$
给定一个$n\times m$的网格，将曼哈顿距离为$2$或$3$的格子之间连一条边，求一条曼哈顿回路。无解输出$Impossible$。
$n,m\leq100$？
$Solution$
$Scape$没讲，咕咕咕。

---

HDU.4700.Flow(构造 最小割树)

$Description$
给定$n$以及$n$个点任意两点之间的最大流，求一张无向图满足给定条件。
$n\leq100$。
$Solution$
有些类似最小割树（可能）。
我们可以构造一棵树，只要让树上的边成为割边，非树边容量为$0$就可以了。
每次找到当前点集中流量最小的边，设其流量为$c$，然后根据$c$将点集分成两个集合，满足两个集合之间的点对的最大流是$c$，集合内部的点的最大流$>c$。对于集合内部继续递归做即可。
划分集合的时候也是可以先随便找一个点$x$划分到左集合，将$flow[x][i]>c$的点$i$分到左集合，其余的点分到右集合，再判断一下左右集合是否满足之间的最大流$=c$即可。注意右集合为空时也无解（$x\dfrac{>c}{}u\dfrac{\ c\ }{}v\dfrac{>c}{}x$，这样显然不行）。
复杂度$O(n^3)$？
注意$A[i]$别写成$i$。。
https://www.cnblogs.com/SovietPower/p/10533310.html

---

TCO2017 Round3 HiddenRabits(2-SAT 树形DP)

$在以x为根的子树中，LCA(y,z)=k\Leftrightarrow x,y,z在k的三个不同的三叉子树里$...？
（或者$y,z$到达$k$都需要经过$x$？）
网上唯一的题解...

---

$Description$

$Solution$

---