@SovietPower
2018-02-04T02:50:35.000000Z
字数 5048
阅读 2551
数论习题
数学,数论
Codeforces757E.Bash Plays With Functions (积性函数)
首先将的式子化为
即为与的狄利克雷卷积。
因为n的所有质因子之间对的贡献是独立的,所以显然为积性函数(为什么我还是不懂。。),那么也为积性函数。
于是可以对每个质因子单独计算,这样狄利克雷卷积就可以化成求和
(的所有因子即)
同时可以发现,即的值与因子p无关,只与次数有关。
那么DP,用表示,则。
询问时对分解质因数即可。
Code.
BZOJ.2301.[HAOI2011]Problem B (莫比乌斯反演)
求
首先是把下界作为1.可以化为求
说明:
首先要求中有多少,再求[1,j]中有多少,显然这个的上界就分别是,答案就是的数对个数。
现在考虑如何求上面的式子。
由莫比乌斯反演,有
设为满足的对数,其中;
为满足的对数,其中。
显然有
又显然有,那么
令,即,令,则
(本题i就是1。)
上面这个式子还是的。。还是要分块计算。
Code.
HDU.5628.Clarke and math (狄利克雷卷积)
给出,求.
首先狄利克雷卷积(Dirichlet Product):设是两个数论函数,它们的Dirichlet乘积也是一个数论函数,
简记为。
狄利克雷卷积有几个性质:
1. 满足交换律
2. 满足结合律
3. 满足分配率
4. 存在单位元,使得
回到本题。设.
将式子依次展开
,即.
,即.
这样下去可以得到。由于狄利克雷卷积满足结合律,所以的狄利克雷卷积可以用快速幂计算。
计算狄利克雷卷积时,如果对每个都按照定义枚举其约数计算,时间肯定爆炸。所以可以枚举约数,再枚举这些约数可以对哪些值给出贡献,那么计算一次狄利克雷卷积的复杂度就是,总复杂度。
Code.
HDU.5698.function (杜教筛)
求.
参考.
设,那么。
如果狄利克雷卷积中左边的一个函数是待求前缀和的,而另外两个函数的前缀和比较好计算,那么就可以简化计算过程。
像之前一样,试着计算一下:
而
step2同之前,就是换做考虑因数贡献的值。
这样。
预处理就用线筛和莫比乌斯反演 暴力枚举约数。(枚举到多少最适合我也不知道==不过其实挺小了。
Code.
BZOJ.3884.上帝与集合的正确用法 (扩展欧拉定理)
给定p,
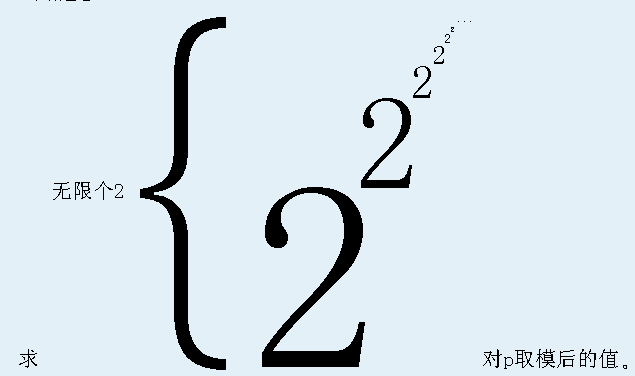
欧拉定理:,则.
扩展欧拉定理: (a为任意整数,b,p为正整数,且(a,p不一定要互质).证明.
指数是无穷的,但是模数是有限的,从不断减小p去考虑。
设,次数是无穷的,所以肯定。根据扩展欧拉定理可得
这样就有了f的递推式,可以直接递归计算。
那么复杂度是多少?
若为偶数,则;若为奇数,则为偶数,转化为偶数的情况。所以最多递归层。
的一个证明:
设,则.
若,则,为偶数。
否则,若,且至少有一个奇素数p,则为偶数(因为两个数都是奇数)。
另官方题解.
Code.
51Nod.1237.最大公约数之和 V3(莫比乌斯反演 杜教筛 欧拉函数)
,求
首先
注意不是!
然后就可以杜教筛了。
最后一步用到
证明:
首先有 (不证了).
设 ,则.
那么
即 .
Code.
