国庆 青岛正睿

正睿OI

Day1

一阶和式？
$n(1+x)^{n-1}=\sum_{i=1}^ni\cdot C_{n,i}\cdot x^{i-1}$

$1\leq p_1\leq p_2\leq\ldots\leq p_k$
$q_i=p_i+i-1$
$1<q_1<q_2<\ldots<q_k$
$p$的个数$\to$满足条件的$q$的个数

第$i$层有$2^i$个节点，要维护的值为$2^i\times\frac{n}{2^i}=O(n)$
$\log$层
通过位运算找到第一个不同的位，就可以找到对应的层。

求所有长度为$k$的区间的乘积。
对$0,k,2k,...$这些点维护前缀积和后缀积。

给定$n$个区间$l_i,r_i$，满足$l_1\leq l_2\leq...\leq l_n,r_1\leq r_2\leq...\leq r_n$，求所有给定区间的乘积和。在线。
令$p=r_1$，往前维护前缀和，对后面跨过$p$的再求后缀和。如果某个区间$i$不再跨过$p$，令$p=r_i$，重新维护前缀和。

Day2

Test：https://www.cnblogs.com/SovietPower/p/9737888.html

我们将开关改变的点设成黑色，不变的点设成白色，将连接不同颜色的点的边的存在性反转（连接同色点的边存在性自然不变）。
这样原题中的每个方案对应一个黑白染色的方案（废话）。
因为连出的边是$O(n^2)$级别的，原图只存在$O(n)$条边，所以不连通的情况非常少，我们考虑算不连通（不合法）的方案数（强行解释?不管了）。

假设按下开关的点为黑点，考虑什么时候某个点为黑点时图不连通。令它在原图上的邻接点为白点，这圈白点之外的全为黑点，那这个点不与任何点有边，即被孤立了。称这个点为孤立点。

题解：考虑两个相邻的同色点，设它们为黑点，那么任何一个白点至少与这两个点之一连通（如果都不连通说明在原图都连通，那就是个环了），即整个白色点集与这两个黑点连通（即白色点不可能成为孤立点）。
那么如果存在黑色点$x$不与这两个黑点连通，则$x$不与任何白点有连边，那么在原树中$x$与所有白点相邻。这样它是一个孤立点。
那么一个点是孤立点当且仅当其相邻点集为整个异色点集。
一个方案合法当且仅当不存在孤立点。

我们发现所有点都可以成为孤立点并使得图不连通，且某个染色方案最多存在一个孤立点（否则两个孤立点都与所有异色点相连，就又不是树了）。
那么我们枚举每个点作为孤立点就可以得到$O(n)$种不合法的染色方案。
因为把所有点颜色取反，所有边的存在性不会改变，所以一个孤立点对应两种不合法的染色

但是某两个点做孤立点时它们的染色方案可能是相同的。
然后我们发现重复的染色情况只可能是叶节点做孤立点。我们把叶节点的情况放到它的邻接点上判就行了（算某个叶子$x$时，如果$fa[x]$标记过，不算再答案；否则标记$fa[x]$算它的答案）。

我们发现还有一种不合法的染色方案，即对一条链交替染色。
当链上有$2,3,4,5$个点时，方案不合法，但都对应某个点是孤立点的情况。
当链上多于$6$个点时，它合法。
当链上有$6$个点时，它仍不合法，但这不对应某个点是孤立点的情况。而且如果是$4$个点的链，链两端各连至少一个叶子（只能是叶子），那么这都是没有被判的不合法情况。
那我们枚举一下边，直接判有没有$4$个点的链且满足它就行了。这样不合法方案数为$(4+2+1)*2=14$种。

上面是神仙rqy的做法。
题解：

再判下特殊情况就完了。
至于为什么只有每个点为孤立点和交替染色这两种方案，或者交替染色只有两种多余不合法方案，不知道。

yjz：你画两分钟图就知道，只有这两种情况了。
...

Day3 AM 图论

https://www.zybuluo.com/SovietPower/note/1304396

Day3 PM DP

预处理$2^0\sim 2^{15}$的表。查$>2^{15}$的数右移$16$位后再查这个表。
就是$O(1)$了。

最小瓶颈生成树

$T(n)=T(\frac n2)+O(n)=O(n)$
同nth_element()。

某题

给定一棵带边权的树。$Q$次询问，每次给定一个数$x$，你需要把一条边的权值改成$x$，求树的最小直径。询问间互不影响。
对于每条边被修改成$x$，有一个函数$\max\{x+C,D\}$，$C$为其两边原直径长度，$D$为两边子树直径的和（常数），函数值为直径长度。
对每条边维护这个函数，对所有的这些函数求个下凸壳或者离线询问或者别的什么的。

某复杂度分析

$T(a+b)=T(a)+T(b)+ab\\\frac{(a+b)^2}{2}=\frac{a^2}{2}+\frac{b^2}{2}+ab$
所以$T(n)=\frac{n^2}{2}$

$O(nV)$的树形依赖背包

决策单调

分治$Solve(l,r,opt_l,opt_r)$。每次选取$mid=(l+r)/2$，找到$opt_{mid}$，递归$Solve(l,mid,opt_l,opt_{mid}),Solve(mid+1,opt_{mid},opt_r)$。
复杂度$O(n\log n)$。
需要可以直接计算DP值（与前面的无关）。

CF 868F

代价可以每次移动当前区间端点算。
端点挪动次数为$O(\sum r-l+opt_r-opt_l)=O(n\log n)$。

BZOJ4709 柠檬

某多重背包

$x个1\to 1个1 \frac x2个2$
$...$
$2x+1个a\to 1个a+x个2a$
$2x+2个a\to 2个a+x个2a$

BZOJ1190 梦幻岛宝珠

把重量表示为$a\times2^b$的形式，然后按$b$排序。
从高到低枚举每一位，$f[i]$表示当前位容量为$i$时的最大价值（容量即$a\times2^{bit}$）。对于同一位，直接$01$背包就行了。
如何转移到下一位？$f[i]$转移到$f[i\times2+\text{W在这一位是否为1}]$即可。注意到每一位的容量不会超过$n\times a_{max}=1000$，所以再对$1000$取$\min$即可。

给定$k$个数，$a_1,a_2,...,a_k$，可以无限用（完全背包），求组成$n$的方案数。
把每个$a_i$拆成$a_i\times 2^0+a_i\times 2^1+...+a_i\times 2^{60}$，按上面的方法做。

某exercise

外面枚举深度，二维状态。

Day4

Test：https://www.cnblogs.com/SovietPower/p/9746504.html

A

用两个单调队列维护前面的最大最小值可以$O(n)$做（一个也可以吧）。这样空间也是$O(n)$的。
注意到数据是随机生成的，一个元素在队列中存在时间的期望为$\frac{1}{n-i+1}$（后面存在比它大/小的元素就出队了）。
所以队列大小只需要$\sum\frac 1i=O(\log n)$就够了。为了方便可以用deque。

B

先考虑$n$个点的有标号生成树怎么计数。
令$f[n]$表示$n$个点的有根树的数量。假设确定根的标号，设除根节点外标号最小的节点所在的子树的大小为$k$（考虑最小标号可以避免重复计数）。
那么$f[n]=n\times\sum_{k=1}^{n-1}f[k]\times\frac{f[n-k]}{n-k}\times C_{n-2}^{k-1}$。
$\frac{1}{n-k}$即，把$n-k$个点的树，根的标号选择方案先除掉（由该树合并上$k$那棵子树）。
$C_{n-2}^{k-1}$即确定根节点标号，且另一个最小标号也确定，从$n-2$个标号中选$k-1$个给$k$的子树（$n-k-1$给另一棵子树)。
最后再乘$n$即根的标号的选择方案。

由上面树的计数，再知道两棵树的最大深度及直径后，我们就可以合并直径了。
令$f[i][j][k]$表示$i$个点，子树最大深度为$j$，直径为$k$，的方案数。
那么$6$个for枚举。$f[n][\max(d_1+1,d_2)][\max(l_1,l_2,d_1+d_2+1)]=n\times\sum_k f[k][d1][l1]\times\frac{f[n-k][d2][l2]}{n-k}\times C_{n-2}^{k-1}$
复杂度$O(n^6)$。

计算直径不超过$k$的树的个数。
令$f[i][j]$表示$i$个点，最大深度为$j$的方案数。
在外层枚举$k$。转移要满足$d_1+d_2+1\leq k$。
$f[n][\max(d_1+1,d_2)]=n\times\sum_k f[k][d1]\times\frac{f[n-k][d2]}{n-k}\times C_{n-2}^{k-1}$
复杂度$O(n^5)$。可以用前缀和优化到$O(n^4)$。

每棵树都有唯一的中心。
如果直径为偶数，那么中心是一个点，否则中心是一条边。
如果中心是一个点，那么中心两旁最大深度的子树至少出现了两次；
否则，直径为奇数，要求合并的两棵子树深度相同。

这样好像就可以得到答案了？
令$f[i][j]$表示$i$个点，深度至多为$j$的方案数。
令$g[i][j]$表示$i$个点，深度恰好为$j$的方案数。
那么
$f[n][i]=n\times\sum_kf[k][i-1]\times\frac{f[n-k][i]}{n-k}\times C_{n-2}^{k-1}$
$g[n][i]=f[n][i]-f[n][i-1]$。

统计答案：
直径为奇数时（设为$2l+1$），枚举直径一边子树大小，同样 令除根外标号最小的点在被合并的子树中。这样根随意确定，根确定后标号最小的点也确定。即方案有$C_{n-1}^{k-1}$种。
即答案为$\sum_kg[k][l]\times g[n-k][l]\times C_{n-1}^{k-1}$。
如图（这图应该在上面就有吧==）：

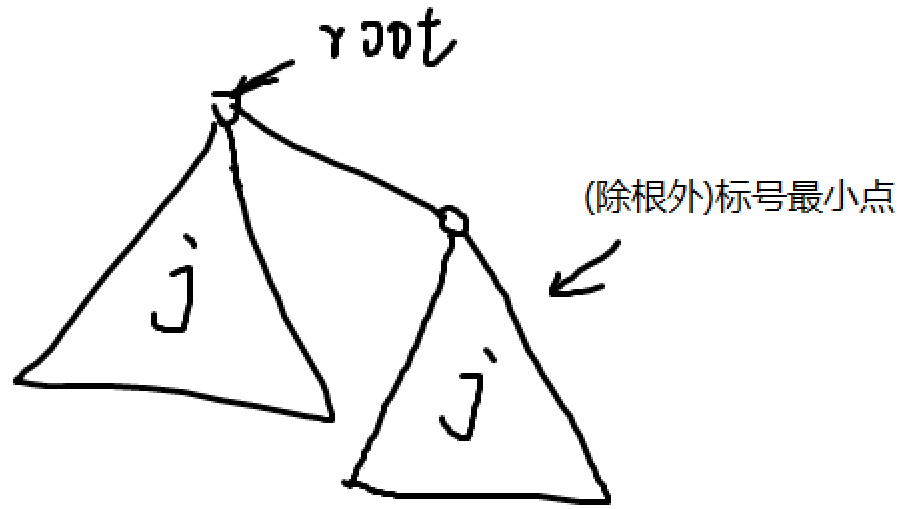
直径为偶数时（设为$2l$），那么答案为有至少两棵深度为$l$的子树的树的方案数。
$g[l][n]$会有不合法情况（最大深度子树只出现了一次）。减掉从$g[l-1][n]$转移到$g[l][n]$时的值就行了（从$l-1$转移到的$l$，最大深度$l$只出现一次）
（即用最大深度为$l$的所有方案，减去某棵最大深度不足$l$的树并上某棵最大深度为$l-1$的树，得到最大深度为$l$的树的方案数）
因为被并上的子树是唯一的（它深度最大（$l-1$）），所以不需要去重，直接分配标号即可（系数为$C_n^k$）。

唯一是指，如图，若$A$子树深度也为$l-1$，那么直接分配标号即可。否则$A$子树深度$<l-1$，肯定不会和$B$相同。

那么答案为$\sum_kg[k][l-1]\times f[n-k][l-1]\times C_{n}^{k}$。

代码实现：
因为直接做常数有点大，只有90分。所以要卡卡常。
组合数要$n^2$预处理。直接用阶乘$O(1)$算还要两次取模。
注意到这个转移（最大深度为第一维，点数为第二维）：f[i][j]=j*Σf[i-1][k]*f[i][j-k]*inv[j-k]*C[j-2][k-1]可以写成f[i][j]=j*fac[j-2]*Σ(f[i-1][k]*ifac[k-1])*(f[i][j-k]*ifac[j-k-1]*inv[j-k])。
我们可以存两个辅助数组f2[i][j]=f[i][j]*ifac[j-1]，f3[i][j]=f[i][j]*ifac[j-1]*inv[j]，这样可以有效减少取模次数。

C

容易看出只要$k$至少为$2$就没有用了。没人住的酒店是合法的当且仅当每个点不是孤立点且它是独立集（之间没有边）。

分数规划，二分答案$x$，求是否存在方案满足$\sum (a[i]-x)\geq0$。
把每个酒店的权值改为$a[i]-x$。这样我们应尽量不选负权值点（即把它们作为没人住的酒店），它需要是独立集。那么我们可以求一个权值和最小的独立集。
负数且求最小权值和很奇怪，反正不妨把权值写成$x-a[i]$，求权值最大的独立集。

$二分图最大权独立集=总权值-最小割$。这样线段树优化建图跑网络流可以得到$60$分。

把所有权值都与$0$取个$\max$。这样就不需要单独考虑负权的了。
考虑对二分图的右侧（右边酒店）DP。令$f[i]$表示到右侧第$i$家酒店且选$i$的最大权值。我们枚举一个$f[j](j<i)$转移，即$j+1\sim i-1$都不选，这样连边区间完全在$j+1\sim i-1$的左侧的点都能选择。
直接枚举是$O(n^3\log v)$的。
可以用前缀和预处理完全包含在区间$[l,r]$内的所有权值和$s[l][r]$。把区间按右端点排序。枚举左端点，然后移动右端点算就行了。
这样就是$O(n^2\log v)$了。

考虑每个区间$[l,r]$的贡献$w$（其实就是个点权），当$j<l,r<i$时，$f[i]=\max\{f[j]+w\}$，即有$w$这个贡献。可以想到区间加。那么线段树维护区间最大值、单点修改、区间加就好了。
复杂度$O(n\log n\log v)$。

Day5 AM 位运算

$2^{31}-1=\sim0u>>1$
自然溢出：对$2^{32}$取模。
对$2^{20}$取模，先自然溢出，最后$Ans\&(2^{20}-1)$。

补码：关于模$2^{32}$同余。$-1=1111...1111=2^{32}-1,-5=2^{32}-5$
$-1$：
原码：$10000001$
反码：$11111110$
补码：$11111111$

$x-=lowbit(x)=x\&(x-1)$

__builtin_popcount(x)，x为int或unsigned int。
__builtin_popcountll(x)，x为long long或unsigned long long。
手写：打$0\sim65535$的表，$ans=cnt[x\&65535]+cnt[x>>16\&65535]$。
__builtin_ffs(x)，判断$n$的二进制末尾最后一个$1$的位置，从$1$开始
__builtin_parity(x)，判断$1$的个数的奇偶性（__builtin_popcount(x)&1）。
__builtin_ctz(x)，__builtin_ctzll(x)，统计$x$末尾$0$的个数（确定最后一个$1$的位置）。
__builtin_clz(x)，__builtin_clzll(x)，前缀$0$的个数。
https://blog.csdn.net/qq_40679299/article/details/80224547

$\lfloor\log_2n\rfloor(n\neq0)=31-\_\_builtin\_popcount(\_clz(x))$。

$(a\oplus b)+((a\&b)<<1)=a+b$
$(a\ \mathbb{and}\ b)+(a\ \mathbb{or}\ b)=a+b$

bitset的访问：$bit[i]==1$。

01卷积 $c[i+j]=OR/XOR\ \ a[i]\&b[j]\to c[i]=OR_{j=0}^ia[n-j]\&b[i-j]\to C=OR_{j=0}^i n(A<<j)\&(B<<j)$
$O(\frac{n^2}{w})$

Day5 PM 树上数据结构

离线的求路径最大值。
DFS+并查集，再把边表反过来，再DFS+并查集。

$k$级祖先。
预处理每个点往上走$1,2,3,...,\sqrt n,2\sqrt n,...n$步到的点。复杂度$O(\sqrt n)$。
查询时先走一步$x\sqrt n$，再走一步$y$。复杂度$O(1)$。
预处理每个点往上走$1,2,3,...,n^{\frac 13},2n^{\frac 13},...n^{\frac 23},2n^{\frac 23},...,n$步到的点。复杂度$O(n^{\frac 43})$。
查询时先走一步大步，再走中步，再走一步小步。复杂度$O(1)$。

离线，维护当前点到每个点的距离。这个可以先求根到所有点的距离，建出线段树。然后每次转移到另一个节点，子树外的所有点到当前点的距离会$+len$，子树内的距离$-len$。线段树区间最大值、区间加就行了。
在线可以可持久化线段树，区间修改可以标记永久化（或者不用）。

每个询问坐标为$(L_u,L_v)$。

欧拉序：每次访问完一个儿子回溯到这个点时要加进去。
括号序：离开这个点时加进去。

ZJOI 大森林
Splay维护括号序。

多次询问求删除$k$条边后树的直径。询问独立。
删除一条边得到的那棵子树，即在DFS序上删掉一段区间。那么$k$条边会把DFS序分成若干区间。用栈维护每个属于某棵被分割的子树的区间。

Day6 AM

$L>1$时取$mid$为几何平均数，即$mid=\sqrt{L\cdot R}$。
相对误差，$0$与$1$之间是相对精度，$>1$为绝对精度。

乘法丢失精度小。

编辑距离

强制端点选 就不会出现重复
枚举第一段在哪转移 就不会重复

Day6 PM

判负环$O(nm)$。

if(dis[v]>dis[u]+w)
    dis[v]=dis[u]+w
    dep[v]=dep[u]+1
    if(dep[v]>n) return;

第一次SPFA预处理$1$到每个点的距离，然后把边权$w(u,v)$改为$w(u,v)+h(u)-h(v)$。
其中$h(u)$为设定的标号，$h(u)=dis[u]$（因为$dis[u]+w(u,v)\geq dis[v]$）

按照反图DFS，出栈序列就是一个合法的拓扑序列。
scc缩点顺序是一个合法拓扑序。