bzoj4017 小Q的无敌异或

bzoj BIT

---

Link:http://www.lydsy.com/JudgeOnline/problem.php?id=4017

题意：有一个长度为 $N$ 的数列，求其

$$\sum 所有子数列异或和$$
以及 $$XORSUM \{子数列求和\}$$

$1 \leq N \leq 10^5,元素 0 \leq A_i \leq 10^6$

Solution

对于第一个子问题，按位计算贡献，即计算ans能加多少个$1 << k$

首先我们计算一下前缀异或和

注：以下就以某一位来讨论

我们维护两个值，$0$ 的个数以及 $1$ 的个数
令当前已经计算了 $k$ 个值的贡献，要计算 $k+1$ 的贡献
如果 $k+1$ 处前缀异或和这一位是 $1$ 则贡献要加上先前 $0$ 的个数，否则要加上 $1$ 的个数 （显然，想要使对最终答案的贡献为 $1$ ，之前一定是 $1 xor 0=1$ 或者 $0 xor 1= 1$）
最后ans直接加上 $(1 << k)\times 贡献值$ 即可

第一问就解决了，时间复杂度 $O(nlog \ max\{A\})$

---

第二个子问题：
答案是异或和，我们不妨按位来考虑，看什么时候会使 $ans$ 的某一位变成 $1$
显然，由异或的性质可知，第 $k$ 位 有奇数个 $1$ 出现时，最终答案的第 $k$ 位才为 $1$
形式化的，我们有

$$(sum(r)-sum(l-1)) mod 2^{k+1} \geq 2^k (r \geq l)$$
此时这题复杂度已经比纯暴力好了非常多，对于每一个 $r$ 统计出所有满足上式的 $l-1$ 的个数，但仍然很高
不过由上面的操作统计先前满足条件的个数，想到可以使用树状数组或线段树来维护， $logn$ 查询

上述式子可以进一步展开，

$$\begin{cases}{sum(l-1)mod2^{k+1}\leq sum(r) mod 2^{k+1}-2^k}\quad\quad(sum(r) mod 2^{k+1}\geq sum(l-1)mod2^{k+1})\\{sum(l-1)mod2^{k+1}\leq sum(r) mod 2^{k+1}+2^k}\quad\quad(sum(r) mod 2^{k+1} < sum(l-1)mod2^{k+1})\end{cases}$$

可以用树状数组分别查询
代码里会看到查询三个值，很诡异，原因见下图

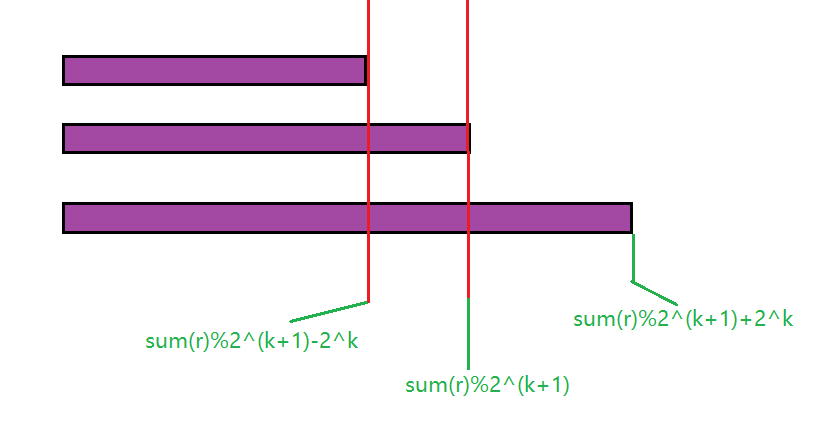
由之前推的两个式子可知，两条红线之间夹的是不可取的地方，我们需要左右两边的值，如果用BIT存奇偶性，查找三个绿色处的前缀，异或起来就可以了(中间部分有两遍异或，相当与不存在)

最后，每一位统计最终的奇偶性，若为奇数，则 $ans|=(1 << k)$

---

ps: $\quad$ $a\ mod \ 2^{k+1}$ 等价于 $a \ \& \ (2^{k+1}-1)$ //二进制考虑一下

---

First Code(奇偶性):

#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
#define MAXN 100010
#define MOD 998244353
using namespace std;
LL n;
LL sum[MAXN];
LL xsum[MAXN];
LL p[MAXN];
LL ans;
bool tree[MAXN];
int lowbit(int x){
    return (x)&(-x);
}
void change(LL pos){
    pos++;
    if(pos==0)
        return;
    LL i;
    for(i=pos;i<=n+1;i+=lowbit(i))
        tree[i]^=1;
}
LL getnum(LL pos){
    LL re=0;LL i;
    pos++;
    for(i=pos;i;i-=lowbit(i))
        re^=tree[i];
    return re;
}
LL getloc(LL x){
    LL l=0,r=n;
    LL ans=-1;
    while(l<=r){
        LL mid=(l+r)>>1;
        if(p[mid]<=x){
            l=mid+1;
            ans=mid;
        }
        else
            r=mid-1;
    }
    return ans;
}
void solve1(){
    LL k;
    LL i;
    LL cnt[2];
    for(k=0;k<=30;k++){
        cnt[0]=cnt[1]=0;
        LL tmp=0;
        for(i=0;i<=n;i++){
            bool tt=xsum[i]&(1<<k);
            tmp+=cnt[tt^1];
            cnt[tt]++;
        }
        ans += (1<<k) * tmp%MOD;
        ans%=MOD;
    }
    printf("%lld ",ans);
}
void solve2(){
    ans=0;
    LL i,k;
    for(k = 0;(1LL << k) <= sum[n];k++){
        LL tmp=0;
        for(i=0;i<=n;i++)
            p[i] = sum[i] & ((1LL << (k+1)) - 1);
        sort(p,p+n+1);
        memset(tree,0,sizeof(tree));
        for(i=0;i<=n;i++){
            LL now = sum[i] & ((1LL << (k + 1)) - 1);
            //printf("%lld %lld\n",now,getloc(now));
            LL t1=getnum(getloc(now-(1LL<<k)));
            LL t2=getnum(getloc(now+(1LL<<k)));
            LL t3=getnum(getloc(now));
            change(getloc(now));
            //printf("--%lld %lld %lld\n",now-(1LL<<k),now+(1LL<<k),now);
            //printf("::%lld %lld %lld\n",t1,t2,t3);
            tmp^=t1^t2^t3;
        }
        if(tmp)
            ans |= (1LL<<k);
    }
    printf("%lld\n",ans);
}
int main(){
    scanf("%lld",&n);
    LL i;
    LL x;
    for(i=1;i<=n;i++){
        scanf("%lld",&x);
        xsum[i]=xsum[i-1]^x;
        sum[i]=sum[i-1]+x;
    }
    solve1();
    solve2();
    return 0;
}

---

Second Code(统计个数):

#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
#define MAXN 100010
#define MOD 998244353
using namespace std;
LL n;
LL sum[MAXN];
LL xsum[MAXN];
LL p[MAXN];
LL ans;
int tree[MAXN];
int lowbit(int x){
    return (x)&(-x);
}
void change(LL pos,int v){
    pos++;
    if(pos==0)
        return;
    LL i;
    for(i=pos;i<=n+1;i+=lowbit(i))
        tree[i]+=v;
}
LL getnum(LL pos){
    LL re=0;LL i;
    pos++;
    for(i=pos;i;i-=lowbit(i))
        re+=tree[i];
    return re;
}
LL getloc(LL x){
    LL l=0,r=n;
    LL ans=-1;
    while(l<=r){
        LL mid=(l+r)>>1;
        if(p[mid]<=x){
            l=mid+1;
            ans=mid;
        }
        else
            r=mid-1;
    }
    return ans;
}
void solve1(){
    LL k;
    LL i;
    LL cnt[2];
    for(k=0;k<=30;k++){
        cnt[0]=cnt[1]=0;
        LL tmp=0;
        for(i=0;i<=n;i++){
            bool tt=xsum[i]&(1<<k);
            tmp+=cnt[tt^1];
            cnt[tt]++;
        }
        ans += (1<<k) * tmp%MOD;
        ans%=MOD;
    }
    printf("%lld ",ans);
}
void solve2(){
    ans=0;
    LL i,k;
    for(k = 0;(1LL << k) <= sum[n];k++){
        LL tmp=0;
        for(i=0;i<=n;i++)
            p[i] = sum[i] & ((1LL << (k+1)) - 1);
        sort(p,p+n+1);
        memset(tree,0,sizeof(tree));
        for(i=0;i<=n;i++){
            LL now = sum[i] & ((1LL << (k + 1)) - 1);
            change(getloc(now),1);
            LL t1=getnum(getloc(now-(1LL<<k)));
            LL t2=getnum(getloc(now+(1LL<<k)));
            LL t3=getnum(getloc(now));
            tmp+=t1+t2-t3;
        }
        if(tmp%2)
            ans |= (1LL<<k);
    }
    printf("%lld\n",ans);
}
int main(){
    scanf("%lld",&n);
    LL i;
    LL x;
    for(i=1;i<=n;i++){
        scanf("%lld",&x);
        xsum[i]=xsum[i-1]^x;
        sum[i]=sum[i-1]+x;
    }
    solve1();
    solve2();
    return 0;
}