@zzzc18 2018-01-18T07:41:28.000000Z 字数 5062 阅读 2045

Variable变量——二元关系

网络流

变量（variable）

【题目描述】

有n个变量w1~w[n]，每个变量可以取W或-W。

有q个条件，形如w[x]<=w[y]或w[x]=w[y]或w[x]

最小化 $\sum W_i+\sum H_i$ 。

【输入数据】

第一行一个整数t表示数据组数。

每组数据第一行四个整数n,W,p,q表示节点数。

接下来p行每行九个整数xi,yi,zi,ai,bi,ci,di,ei,fi。

接下来q行每行三个整数x,y,r。

r=0表示w[x]<=w[y]；r=1表示w[x]=w[y]；r=2表示w[x]

保证存在方案。

【输出数据】

每组数据输出一行一个整数表示 $\sum W_i+\sum H_i$ 的最小值。

【样例输入】

1

3 1 1 1

1 2 3 1 1 1 1 1 1 

1 2 2

【样例输出】

【数据范围】

对于30%的数据，n<=15，p,q<=20。

对于100%的数据，t<=10，n<=500，p,q<=1000。

Solution:

首先，由计算 $H_i$ 的式子可以发现两点，只有 $w[x_i],w[y_i]$ 等取不同的值时，才会对 $H_i$ 产生影响；W只是一个系数，可以直接提出来最后算，变量的值为 $1,-1$ 。

这个题满足一个二元关系的形式。

二元关系：

例如：有n个任务，可以选择A任务或者B任务，代价分别是a,b，还有一些三元组关系，[x,y,z]表示如果x任务和y任务选的任务不同，将会有一个额外的代价z，现在分配任务，使总代价最小。

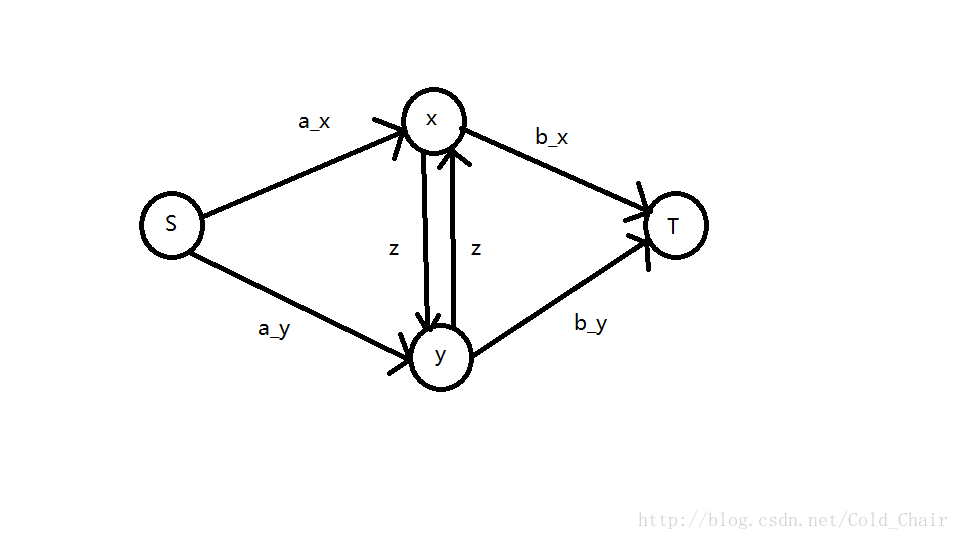
image_1c441t7e314eh1uae1ogf10881nt09.png-24.5kB
图片来源

上面这个图是一个流网络，连到 $S$ 的点表示选择 $A$ 任务，连到 $T$ 的点表示选择 $B$ 任务，其实很形象。
如果要割断 $S,T$ 有两类方法：
1.同时割掉 $a_x,a_y$ 或同时割掉 $b_x,b_y$
2.割掉 $a_x,b_y$ 以及中间的 $z$ ，或者割掉 $a_y,b_x$ 以及中间的 $z$

方案1.就表示 $x,y$ 相同，没有额外代价
方案2.就表示 $x,y$ 不同，有额外代价 $z$

（就说这么多吧，足够这个题了，详见上方的图片来源）

以 $x,y$ 为例（已经将 $W$ 提出）
1.如果 $w[x_i],w[y_i]$ 取不同的值时，答案一定会增加（哪怕增加 $0$ ）
2.如果 $w[x_i]=-1$ ，没有绝对值得部分对答案的贡献为 $-(d-f)-1$ ，同理当 $w[x_i]=1$ 时对答案的贡献为 $(d-f)+1$

由上面的二元关系，直接就可以建图出来。

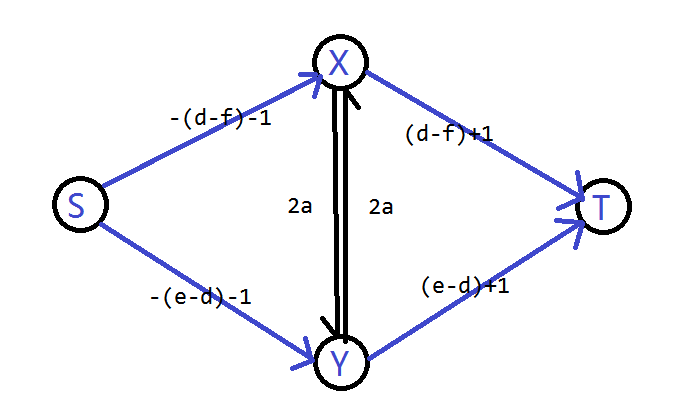
image_1c442o6r18jh1pnb1in01shk1i4mm.png-19.9kB

题目中还有一些其他限制
1.对于 $x<y$ ,连 $x,T$ 边权为 $\infty$ ,连 $S,y$ 边权为 $\infty$ 。表示 $w[x]$ 必须取 $-1$ , $w[x]$ 必须取 $1$ （不然网络割不断）
2.对于 $x=y$ ,连 $x,y$ ， $y,x$ ，边权为 $\infty$
3.对于 $x<=y$ ,连 $x,y$ ，边权为 $\infty$

最后跑最小割即可

注：

1.不要忘了答案最后要乘 W
2.对于负边权，没法跑最小割，有两种解决方法，一种把建图方式改一改，另一种直接把连到 S,T 的边权加上 OFFSET，最后最小割减去 n*OFFSET

//OFFSET法
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 500+9;
int n,W,p,q;
LL val[MAXN];
const LL INF = 2000000000000000LL;
const LL OFFSET = 10000000000LL;
int S,T;
struct E{
    int next,to;
    LL val;
}edge[MAXN*MAXN*20];
int head[MAXN],iter[MAXN];
int edge_num;
int depth[MAXN];
void addedge(int x,int y,LL val){
    edge[++edge_num].next=head[x];
    edge[edge_num].to=y;
    edge[edge_num].val=val;
    head[x]=edge_num;
}
void link(int x,int y,LL val){
    addedge(x,y,val);
    addedge(y,x,0);
}
void Clean_Edge(){
    memset(head,0,sizeof(head));
    edge_num=1;
}
bool BFS(int s,int t){
    static queue<int> que;
    que.push(s);
    memset(depth,-1,sizeof(depth));
    depth[s]=1;
    while(!que.empty()){
        int fro=que.front();que.pop();
        for(int i=head[fro];i;i=edge[i].next){
            if(edge[i].val>0 && depth[edge[i].to]==-1){
                depth[edge[i].to]=depth[fro]+1;
                que.push(edge[i].to);
            }
        }
    }
    return depth[t]!=-1;
}
LL DFS(int x,int goal,LL val){
    if(x==goal){
        return val;
    }
    for(int &i=iter[x];i;i=edge[i].next){
        if(edge[i].val>0 && depth[edge[i].to]==depth[x]+1){
            LL tmp=DFS(edge[i].to,goal,min(val,edge[i].val));
            if(tmp>0){
                edge[i].val-=tmp;
                edge[i^1].val+=tmp;
                return tmp;
            }
        }
    }
    return 0;
}
LL Dinic(int s,int t){
    LL re=0;
    while(BFS(s,t)){
        memcpy(iter,head,sizeof(head));
        while(true){
            LL tmp=DFS(s,t,INF);
            if(tmp==0)break;
            re+=tmp;
        }
    }
    return re;
}
int main(){
    /*solution:blog.csdn.net/u011056504/article/details/78997980*/
    freopen("variable.in","r",stdin);
    freopen("variable.out","w",stdout);
    int kase;
    scanf("%d",&kase);
    while(kase--){
        scanf("%d%d%d%d",&n,&W,&p,&q);
        S=0;T=n+1;
        for(int i=1;i<=n;i++)
            val[i]=0;
        Clean_Edge();
        for(int i=1;i<=p;i++){
            int x,y,z,a,b,c,d,e,f;
            scanf("%d%d%d%d%d%d%d%d%d",&x,&y,&z,&a,&b,&c,&d,&e,&f);
            link(x,y,2*a);link(y,x,2*a);
            link(y,z,2*b);link(z,y,2*b);
            link(x,z,2*c);link(z,x,2*c);
            val[x]+=d-f;
            val[y]+=e-d;
            val[z]+=f-e;
        }
        for(int i=1;i<=q;i++){
            int x,y,r;
            scanf("%d%d%d",&x,&y,&r);
            if(r==0)
                link(x,y,INF);
            if(r==1){
                link(x,y,INF);
                link(y,x,INF);
            }
            if(r==2){
                link(x,T,INF);
                link(S,y,INF);
            }
        }
        LL ans=0;
        for(int i=1;i<=n;i++){
            link(S,i,-val[i]-1+OFFSET);
            link(i,T,val[i]+1+OFFSET);
        }
        ans=Dinic(S,T);
        printf("%lld\n",(ans-n*OFFSET)*W);
    }
    return 0;
}

//另一种方法
#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define inf 1e9
#define L long long
using namespace std;
const int MaxV = 510, MaxE = 20010;
namespace dinic{
    struct edge{
        int to, nxt, cap;
    }e[MaxE]; int cnt = 1, lst[MaxV];
    void ins(int a, int b, int c){ e[++cnt] = (edge){b, lst[a], c}; lst[a] = cnt;}
    void lnk(int a, int b, int c){ ins(a, b, c); ins(b, a, 0);}
    int h[MaxV]; queue<int>q;
    bool bfs(int s, int t){
        memset(h, -1, sizeof(h));
        h[s] = 0; q.push(s);
        while(!q.empty()){
            int c = q.front(); q.pop();
            for(int i=lst[c], b; b = e[i].to, i; i = e[i].nxt){
                if(!~h[b] && e[i].cap > 0){
                    h[b] = h[c] + 1;
                    q.push(b);
                }
            }
        }
        return ~h[t];
    }
    int dfs(int v, int t, int f){
        if(v == t) return f;
        int used = 0, w;
        for(int i = lst[v], b; b = e[i].to, i; i = e[i].nxt)
            if(h[b] > h[v] && e[i].cap > 0){
                w = dfs(b, t, min(f - used, e[i].cap));
                e[i].cap -= w; e[i ^ 1].cap += w;
                if((used += w) == f) return f; 
            }
        if(!used) h[v] = -1;
        return used;
    }
    int max_flow(int s, int t){
        int ans = 0;
        while(bfs(s, t))
        {
            int k=dfs(s, t, 1e9);
            if(k>1e8)
                return -1;
            ans += k;
        }
        return ans;    
    } 
    void clear()
    {
        memset(lst, 0, sizeof(lst)), cnt = 1;
    }
}
using dinic::lnk;
using dinic::max_flow;
using dinic::clear;
int t,n,m,p,q,x,y,z,a,b,c,d,e,f,u[510],ans;
int main()
{
    freopen("variable.in","r",stdin);
    //freopen("variable.out","w",stdout);
    int i;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d%d%d",&n,&m,&p,&q);
        for(i=1;i<=n;i++)
            u[i]=1;
        for(i=1;i<=p;i++)
        {
            scanf("%d%d%d%d%d%d%d%d%d",&x,&y,&z,&a,&b,&c,&d,&e,&f);
            lnk(x,y,2*a);
            lnk(y,x,2*a);
            lnk(y,z,2*b);
            lnk(z,y,2*b);
            lnk(x,z,2*c);
            lnk(z,x,2*c);
            u[x]+=d-f;
            u[y]+=e-d;
            u[z]+=f-e;
        }
        for(i=1;i<=q;i++)
        {
            scanf("%d%d%d",&x,&y,&z);
            if(z==1)
            {
                lnk(x,y,inf);
                lnk(y,x,inf);
            }
            else if(z==2)
            {
                lnk(x,n+1,inf);
                lnk(0,y,inf);
            }
            else
                lnk(x,y,inf);
        }
        for(i=1;i<=n;i++)
        {
            ans-=abs(u[i]);
            if(u[i]>0)
                lnk(i,n+1,2*u[i]);
            else if(u[i]<0)
                lnk(0,i,-2*u[i]);
        }
        for(int i=2;i<=dinic::cnt;i++)
            printf("%d %d\n",dinic::e[i].to,dinic::e[i].cap);
        ans+=max_flow(0,n+1);
        printf("%lld\n",(L)ans*m);
        ans=0;
        clear();
    }
    return 0;
}

Variable变量——二元关系

变量（variable）

Solution:

二元关系：

内容目录