算法概论实验十一

算法概论实验

实验十一
实验目的与要求：
（1） 掌握对无向图的2-连通分量的划分算法。
（2） 理解与掌握在含负权值边的图中求最短路径问题的算法。
1．无向图的双连通分量问题
【问题描述】
给定一个无向图，设计一个算法，判断该图中是否存在关节点，并划分双连通分量。
2．带负权值边的有向图中的最短路径路径问题
【问题描述】
对于一个带负权值边的有向图，实现Bellman-Ford算法，求出从指定顶点s到其余顶点的最短路径，并判断图中是否存在负环。

1．无向图的双连通分量问题

1.1结构化定义

//为了方便输出双联通分量，定义一个结构
struct myedge
{
    int start;
    int end;
    myedge(int a, int b)
    {
        start = a;
        end = b;
    }
};

template<class T>
class MGraph
{
public:
    MGraph(T v[], int n, int e);//无向图的邻接矩阵建立
    MGraph();
    virtual ~MGraph();
    void Print();//打印图
    void print_prepost();//打印prepostback表
    int BiDFS(int v);//关节点
private:
    int vexnum, edgenum;    //vexnum--顶点数 edgenum--边数
    vector<vector<int> > edges;   //邻接矩阵 
    vector<vector<bool> > edges_view;   //领街边判定表
    vector<T> vexs;         //顶点表
    vector<int> pre; 
    vector<int> post;
    vector<int> back;
    vector<int> vex_cnt;  //输出辅助计数器
    stack<myedge> edgeStack;//边集存储
    int clock;
    int gettruenum();   //获取判断表中true数量
    bool getVexV(int v);//判断是否存在未访问边
    myedge getFirstVw(int v);//找到vw边
    vector<vector<int>> show_edge;
};

1.2 关键函数

//Bicomponent Algorithm 
template<class T>
int MGraph<T>::BiDFS(int v)
{
    pre[v] = clock;
    clock++;
    back[v] = pre[v];
    while (getVexV(v))
    {
        myedge t = getFirstVw(v);
        edgeStack.push(t);
        vex_cnt[t.start]++;//辅助保存start出现次数
        if (pre[t.end] == -1)//如果是tree边
        {
            int wBack = BiDFS(t.end);
            if (wBack >= pre[v])
            {
                cout << "双连通分量:" << endl;
                int tmp = edgeStack.top().end;
                if (vex_cnt[tmp] > 0)
                {
                    while (edgeStack.top().start != tmp)
                    {
                        cout << vexs[edgeStack.top().start] << "->" << vexs[edgeStack.top().end] << endl;
                        vex_cnt[edgeStack.top().start]--;
                        edgeStack.pop();
                    }
                }
                cout << vexs[edgeStack.top().start] << "->" << vexs[edgeStack.top().end] << endl;
                vex_cnt[edgeStack.top().start]--;
                edgeStack.pop();
            }
            back[v] = min(back[v], wBack);
        }
        else
        {
            back[v] = min(pre[t.end], back[v]);
        }
    }
    post[v] = clock;
    clock++;
    return back[v];
}

1.3 测试函数

int main()
{
    //char a[] = { '1', '2', '3', '4', '5','6','7','8' };
    char a[] = { 'A', 'B', 'C', 'D', 'E','F','G','H','I','J' };
    MGraph<char> m(a, 10, 14);
    cout << endl << "打印测试：" << endl;
    m.Print();
    cout << endl << "关节点测试测试：" << endl;
    m.BiDFS(9);
    cout << endl;
    cout << "pre/post/back值测试：\n";
    m.print_prepost();
    return 0;
}

1.4 测试截图

2理解与掌握在含负权值边的图中求最短路径问题的算法

简单，易理解 从源点出发，做V-1次大循环，每次对所有边进行松弛更新

2.1BellmanFord

template <class T>
bool MGraph<T>::BellmanFord(int source)
{
    dist[source] = 0;
    for (int i = 1; i <= vexnum - 1; i++)
    {
        for (int u = 0; u < vexnum;u++)
        {
            for (int v = 0; v<vexnum;v++)
            {
                if (edges_view[u][v]==true)
                {
                    update(u, v, edges[u][v]);
                }
            }
        }
    }
    // 判断是否有负环路
    for (int u = 0; u < vexnum; u++)
    {
        for (int v = 0; v < vexnum; v++)
        {
            if (edges_view[u][v] == true)
            {
                if (dist[v] > dist[u] + edges[u][v])
                {
                    return false;
                }
            }
        }
    }
    return true;
}

2.2更新

template <class T>
void MGraph<T>::update(int u, int v, int weight)
{
    if (dist[v] > dist[u] + weight)
        dist[v] = dist[u] + weight;
}

2.3测试函数

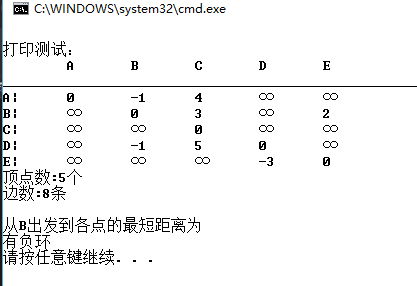
int main()
{
    //char a[] = { 's', '2', '3', '4', '5','6','7','t' };
    //char a[] = { 'A', 'B', 'C', 'D', 'E','F','G','H','I','J' };
    char a[] = { 'A', 'B', 'C', 'D', 'E'};
    MGraph<char> m(a, 5, 8);
    cout << endl << "打印测试：" << endl;
    m.Print();
    m.Print_dist(1);
    return 0;
}

2.4测试截图