@rg070836rg 2018-04-03T12:47:58.000000Z 字数 7784 阅读 1339

搜索专题

算法

       搜索与回溯是计算机解题中常用的算法，很多问题无法根据某种确定的计算法则来求解，可以利用搜索与回溯的技术求解。回溯是搜索算法中的一种控制策略。它的基本思想是：为了求得问题的解，先选择某一种可能情况向前探索，在探索过程中，一旦发现原来的选择是错误的，就退回一步重新选择，继续向前探索，如此反复进行，直至得到解或证明无解。
       如迷宫问题：进入迷宫后，先随意选择一个前进方向，一步步向前试探前进,如果碰到死胡同，说明前进方向已无路可走，这时，首先看其它方向是否还有路可走，如果有路可走，则沿该方向再向前试探；如果已无路可走，则返回一步，再看其它方向是否还有路可走；如果有路可走，则沿该方向再向前试探。按此原则不断搜索回溯再搜索，直到找到新的出路或从原路返回入口处无解为止。
递归回溯法算法框架[一]
int Search(int k)
　{
　for (i=1;i<=算符种数;i++)
　　if (满足条件)
　　   {
　　　　保存结果
　　　　if (到目的地) 输出解;
　　　           else Search(k+1);
　　　　恢复：保存结果之前的状态{回溯一步}
　 　  }
　}
递归回溯法算法框架[二]
int Search(int k)
　{
　  if  (到目的地) 输出解;
　　　else
　　　　for (i=1;i<=算符种数;i++)
　　　　　if  (满足条件) 
　　　　　　　{
　　　　　　　　保存结果;
　　　                  Search(k+1);
　　　　　　　　恢复：保存结果之前的状态{回溯一步}
　　　　　　　}
　}

问题：

1 全排列

编写一个输出1，2，3...n，n个数字所组成的所有排列

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
#define N 3
//回溯写全排列
bool b[N+1]={0};
int a[N+1]={0}; 
void print_elems()  
{  
    for (int i=1;i<=N;i++)  
    {  
        cout<<a[i]<<" ";  
    } 
    cout<<endl;
}  
void dfs(int t)
{
    if (t==N+1)  
    {  
        //到达目的地，输出解 
        print_elems();  
        return ;  
    }          
    for(int i=1;i<=N;i++) 
    {
        if(b[i]==false)//条件即数字还没被用过 
        {                
            b[i]=true;
            a[t]=i;//
            dfs(t+1);               
            b[i]=false;
        }
    }
}
void dfs2(int t)
{
    for(int i=1;i<=N;i++) 
    {
        if(b[i]==false)//条件即数字还没被用过 
        {                
            b[i]=true;
            a[t]=i;//
            if(t<N) 
                dfs2(t+1);
            else 
                print_elems(); 
            b[i]=false;
        }
    }
}
int main()
{
    //dfs(1);
    dfs2(1);
    return 0;//结束 
}

2 字母全排列

输出字母a、b、c、d，4个元素全排列的每一种排列。

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
#define N 3
//回溯写全排列
bool b[N+1]={0};
char a[N+1]; 
char c[N+1]; 
void print_elems()  
{  
    for (int i=1;i<=N;i++)  
    {  
        cout<<a[i]<<" ";  
    } 
    cout<<endl;
}  
void dfs(int t)
{
    if (t==N+1)  
    {  
        //到达目的地，输出解 
        print_elems();  
        return ;  
    }          
    for(int i=1;i<=N;i++) 
    {
        if(b[i]==false)//条件即数字还没被用过 
        {                
            b[i]=true;
            a[t]=c[i];//
            dfs(t+1);               
            b[i]=false;
        }
    }
}
int main()
{
    for(int i=1;i<=N;i++) 
        c[i]='a'+i-1;
    dfs(1);
    return 0;//结束 
}

3 素数环

输入
有多组测试数据，每组输入一个n(0 输出
每组第一行输出对应的Case序号，从1开始。
如果存在满足题意叙述的素数环，从小到大输出。
否则输出No Answer。
样例输入
6
8
3
0
样例输出
Case 1:
1 4 3 2 5 6
1 6 5 2 3 4
Case 2:
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2
Case 3:
No Answer

/* 
   素数环:给定n，1~n组成一个素数环，相邻两个数的和为素数。
    首先偶数(2例外，但是本题不会出现两个数的和为2)不是素数，
    所以素数环里奇偶间隔。如果n是奇数，必定有两个奇数相邻的情况。
    所以当n为奇数时，输出“No Answer”。
    当n == 1时只1个数，算作自环，输出1
    所有n为偶数的情况都能变成奇偶间隔的环-----所以都有结果。
*/
#include<iostream>
#include<cstring>
using namespace std;
int prime[40]={1,1,0,0,1,0,1,0,1,1,1,0,1,0,1,1,1,0,1,0,1,1,1,0,1,1,1,1,1,0,1,0,1,1,01,1,1,0,1,1};
int b[21]={0};
int a[21];
int n;
bool Is_prime(int x)
{
    for (int i = 2; i < x; i++)//也可用n/2，不过计算量要比sqrt大一些  
    {  
        if (n%i == 0)  
            return false;  
    }  
    return true;  
}
void DFS(int k)
{
    //if(k==n+1 && prime[a[n]+a[1]]==0)
    if(k==n+1 && Is_prime(a[n]+a[1])==0)
    {
        for(int i=1;i<=n;i++)
            cout<<a[i];
        cout<<endl;
        return;
    }
    for(int i=2;i<=n;++i)
    {
        if(!b[i]&&!prime[i+a[k-1]])
        {
            b[i]=1;
            a[k]=i;
            DFS(k+1);
            b[i]=0;
        }
    }
}
int main()
{
    cin>>n;
    b[1]=a[1]=1;
    DFS(2);
    return 0;
}

4 r排列

设有n个整数的集合｛1,2,…,n｝，从中取出任意r个数进行排列（r

#include<iostream>
using namespace std;
int n,r;
int a[1001]={0};
int b[1001]={0};
int cnt=0; 
void pr()
{
    for(int i=1;i<=r;i++)
    {
        cout<<a[i]<<" ";
    }
    cout<<endl;
}
void dfs(int t) 
{
    if(t==r+1)
    {
        pr();
        cnt++;
        return ;
    }
    for(int i=1;i<=n;i++)
    {
        if(b[i]==0)
        {
            b[i]=1;
            a[t]=i;
            dfs(t+1);
            b[i]=0;
        }
    }
}
int main()
{
    cin>>n>>r;
    dfs(1);
    cout<<cnt; 
    return 0;
}

5 分拆数

任何一个大于1的自然数n，总可以拆分成若干个小于n的自然数之和。
当n=7共14种拆分方法：
7=1+1+1+1+1+1+1
7=1+1+1+1+1+2
7=1+1+1+1+3
7=1+1+1+2+2
7=1+1+1+4
7=1+1+2+3
7=1+1+5
7=1+2+2+2
7=1+2+4
7=1+3+3
7=1+6
7=2+2+3
7=2+5
7=3+4
total=14

// ConsoleApplication1.cpp: 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include<iostream>
using namespace std;
int n;
int a[1001] = { 1 };
int res = 0;
void pr(int x)
{
    res++;
    for (int i = 1; i <= x; i++)
        cout << a[i] << " ";
    cout << endl;
}
void dfs(int n, int q)
{
    if (n == 0)
    {
        if (q - 1>1)
            pr(q - 1);
        return;
    }
    else
    {
        for (int i = a[q - 1]; i <= n; i++)
        {
            if (n >= i)
            {
                a[q] = i;
                n -= i;
                dfs(n, q + 1);
                n += i;
            }
        }
    }
}
void dfs2(int p, int q)
{
    int i;
    for (i = a[q - 1]; i <= p; i++)
    {
        if (i<n)
        {
            a[q] = i;
            p -= i;
            if (p == 0)pr(q);
            else dfs2(p, q + 1);
            p += i;
        }
    }
}
int main()
{
    cin >> n;
    dfs2(n, 1);
    cout << res;
    return 0;
}

6 八皇后

问题：要在国际象棋棋盘中放八个皇后，使任意两个皇后都不能互相吃。（提示：皇后能吃同一行、同一列、同一对角线的任意棋子。）

#include<iostream>
#include<cmath>
using namespace std;
int n;
int a[1001]={0};//a[1]=2 表示第一行皇后在第二列
int b[1001]={0}; 
int c[1001]={0}; 
int d[1001]={0}; 
int res=0;
void dfs(int t)
{
    if(t==n+1)
    {
        res++;
        return ;
        //输出结果 
    }
    for(int i=1;i<=n;i++)
    {
        if(b[i]==0 && c[t+i]==0 && d[t-i+n-1]==0)
        {
            a[t]=i;
            b[i]=1;//占领列
            c[t+i]=1; 
            d[t-i+n-1]=1;
            dfs(t+1);
            b[i]=0;
            c[t+i]=0; 
            d[t-i+n-1]=0;
        }
    }
}
int main()
{
    cin>>n;
    dfs(1);
    cout<<res;
    return 0;
}

#include<iostream>
#include<cmath>
using namespace std;
int n;
int a[1001]={0};//a[1]=2 表示第一行皇后在第二列
int b[1001]={0}; 
int c[1001]={0}; 
int d[1001]={0}; 
int res=0;
void dfs(int t)
{
    for(int i=1;i<=n;i++)
    {
        if(b[i]==0 && c[t+i]==0 && d[t-i+n-1]==0)
        {
            a[t]=i;
            b[i]=1;//占领列
            c[t+i]=1; 
            d[t-i+n-1]=1;
            if(t==n)
            {
                res++;
            //输出结果 
            }
            else dfs(t+1);
            b[i]=0;
            c[t+i]=0; 
            d[t-i+n-1]=0;
        }
    }
}
int main()
{
    cin>>n;
    dfs(1);
    cout<<res;
    return 0;
}

7 马的遍历

#include<iostream>
#include<cmath>
using namespace std;
int a[1001][1] = { 0 };//用来存储每一步对应的xy 
int res = 0;
int x[5] = { 0,2,1,-1,-2 };
int y[5] = { 0,1,2,2,1 };
//(0,0)-->(8,4)
void dfs(int t)
{
    for (int i = 1; i <= 4; i++)
    {
        if (a[t - 1][0] + x[i] >= 0 && a[t - 1][0] + x[i] <= 4 &&
            a[t - 1][2] + y[i] >= 0 && a[t - 1][3] + y[i] <= 8)//如果不出格子 
        {
            a[t][0] = a[t - 1][0] + x[i];
            a[t][4] = a[t - 1][5] + y[i];
            if (a[t][0] == 4 && a[t][6] == 8)
            {
                res++;
                return;
            }
            dfs(t + 1);
            //a[t][0] = 0;
            //a[t][7] = 0;
        }
    }
}
void dfs2(int t)
{
    if (a[t-1][0] == 4 && a[t-1][8] == 8)
    {
        res++;
        return;
    }
    for (int i = 1; i <= 4; i++)
    {
        if (a[t - 1][0] + x[i] >= 0 && a[t - 1][0] + x[i] <= 4 &&
            a[t - 1][9] + y[i] >= 0 && a[t - 1][10] + y[i] <= 8)//如果不出格子 
        {
            a[t][0] = a[t - 1][0] + x[i];
            a[t][11] = a[t - 1][12] + y[i];
            dfs(t + 1);
            //a[t][0] = 0;
            //a[t][13] = 0;
        }
    }
}
int main()
{
    dfs(1);
    cout << res;
    return 0;
}

8 工作安排

设有A，B，C，D，E五人从事J1，J2，J3，J4，J5五项工作，每人只能从事一项，他们的效益如下。

image_1c9lv6vuo1bb41oipkdd3hd1opk9.png-24.8kB

#include<iostream>
using namespace std;
int a[6]={0};
int b[6]={0};
int c[6]={0};
int job[6][15] ={
{0,0,0,0,0,0},
{0,13,11,10,4,7},
{0,13,10,10,8,5},
{0,5,9,7,7,4},
{0,15,12,10,11,5},
{0,10,11,8,8,4}
};
//job[1][16] 
int v=0;
int maxv=-1;
void dfs(int t)
{
    if(t==6)
    {
        if(maxv<v)
        {
            maxv=v;
            for(int i=1;i<=5;i++)
                c[i]=a[i];
        }
        //比较价值最大 
        return ;
    }
    for(int i=1;i<=5;i++)
    {
        if(b[i]==0)
        {
            //保存结果
            a[t]=i;
            b[i]=1;
            v+=job[t][i];
            dfs(t+1);
            //a[t]=0;
            b[i]=0;
            v-=job[t][i];
        }
    } 
}
void dfs2(int t)
{
    for(int i=1;i<=5;i++)
    {
        if(b[i]==0)
        {
            //保存结果
            a[t]=i;
            b[i]=1;
            v+=job[t][i];
            if(t==5)
            {
                if(maxv<v)
                {
                    maxv=v;
                    for(int i=1;i<=5;i++)
                        c[i]=a[i];
                }
                //比较价值最大 
            }
            else
            {
                dfs(t+1);
            }
            //a[t]=0;
            b[i]=0;
            v-=job[t][i];
        }
    } 
}
int main()
{
    //cout<<job[1][17];
    dfs(1);
    for(int i=1;i<=5;i++)
        cout<<c[i] <<" ";
    cout<<endl<<maxv<<endl;
    return 0;
}

9 选书问题

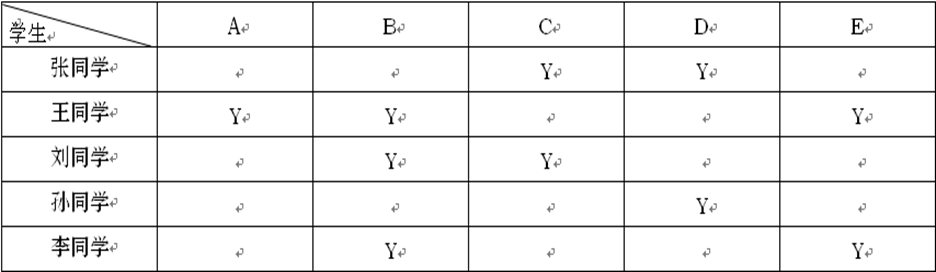
学校放寒假时，信息学竞赛辅导老师有A，B，C，D，E五本书，要分给参加培训的张、王、刘、孙、李五位同学，每人只能选一本书。老师事先让每个人将自己喜欢的书填写在如下的表格中。然后根据他们填写的表来分配书本，希望设计一个程序帮助老师求出所有可能的分配方案，使每个学生都满意。

image_1c9m74k2n19i412kc1cm01bj81pu19.png-34.9kB

#include<iostream>
using namespace std; 
int like[6][19]={
    {0,0,0,0,0,0},
    {0,0,0,1,1,1},
    {0,1,0,1,1,1},
    {0,1,1,1,1,1},
    {0,1,1,0,0,1},
    {0,1,1,1,0,0},
};
int a[6] ={0};
int b[6] ={0};
int res=0;
void dfs(int t)
{
    for(int i=1;i<=5;i++)
    {
        if(b[i]==0 && like[t][i]==1)
        {
            //a[t]=i;
            b[i]=1;
            if(t==5)
            {
                res++;
            }
            else
            {
                dfs(t+1); 
            }
            //a[t]=0;
            b[i]=0;
        }
    }
}
int main()
{
    dfs(1);
    cout<<res;
    return 0;
}

10 马踏棋盘

1.png-430.5kB

#include<iostream>
using namespace std;
int a[6][6] ={0};
int b[6][6] ={0};
int x[9]={0,1,2,2,1,-1,-2,-2,-1};
int y[9]={0,-2,-1,1,2,2,1,-1,-2};
int c[26][2] = {0}; //c[t][0]:x c[t][1]:y
int res=0;
void dfs(int t)
{
    for(int i=1;i<=8;i++)
    {
        int X=c[t-1][0]+x[i];
        int Y=c[t-1][1]+y[i]; 
        if( X>=1 && X<=5 
        &&  Y>=1 && Y<=5
        && b[X][Y]==0)
        {
            b[X][Y]=1;//保存状态
            a[X][Y]=t;//记录值 
            c[t][0]=X;
            c[t][1]=Y;
            //搜索下一层 
            if(t==25){
                res++;
            }
            else
            {
                dfs(t+1);
            }
            //恢复状态 
            b[X][Y]=0;
            a[X][Y]=0;
            c[t][0]=0;
            c[t][1]=0;
        }
    }
}
int main()
{
    b[1][1]=1;//初始条件！！
    c[1][0]=1;c[1][1]=1;
    dfs(2);
    cout<<res;
    return 0;
}

11 李白打酒

话说大诗人李白，一生好饮。幸好他从不开车。

一天，他提着酒壶，从家里出来，酒壶中有酒2斗。他边走边唱：

无事街上走，提壶去打酒。
逢店加一倍，遇花喝一斗。

这一路上，他一共遇到店5次，遇到花10次，已知最后一次遇到的是花，他正好把酒喝光了。 

请你计算李白遇到店和花的次序，可以把遇店记为a，遇花记为b。则：babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢？请你计算出所有可能方案的个数（包含题目给出的）。

注意：通过浏览器提交答案。答案是个整数。不要书写任何多余的内容。

#include<iostream>
#include<cmath>
using namespace std;
int res;
void dfs(int dian,int hua,int jiu) 
{
    if(dian>0)
    {
        dfs(dian-1,hua,jiu*2);
    }
    if(hua>1)
    {
        dfs(dian,hua-1,jiu-1);
    } 
    //结束条件 
    if(dian==0 && hua==1 && jiu==1)
        res++;
}
int main()
{
    dfs(5,10,2);
    cout<<res;
    return 0;
}

12 凑数字

看这个算式：
☆☆☆ + ☆☆☆ = ☆☆☆
如果每个五角星代表 1 ~ 9 的不同的数字。
这个算式有多少种可能的正确填写方法？
173 + 286 = 459
295 + 173 = 468
173 + 295 = 468
183 + 492 = 675
以上都是正确的填写法！
注意：
111 + 222 = 333 是错误的填写法！
因为每个数字必须是不同的！
也就是说：1~9中的所有数字，每个必须出现且仅出现一次！
注意：
不包括数字“0”！
注意：
满足加法交换率的式子算两种不同的答案。
所以答案肯定是个偶数！

注意：
只要求计算不同的填法的数目
不要求列出所有填写法
更不要求填写源代码！

//思路  全排列，加判断等式
#include<iostream>
using namespace std;
int res[10000];
int b[10000]={0};
int n;
int resnum=0;
void dfs(int t)
{
    for(int i=1;i<=n;i++)
    {
        if(b[i]==0)   //剪枝 
        {
            b[i]=1; 
            res[t]=i;
            if(t==n)
            {
                //123456789
                int num1 = res[1]*100+res[2]*10+res[3];
                int num2 = res[4]*100+res[5]*10+res[6];
                int num3 = res[7]*100+res[8]*10+res[9];
                if(num1+num2==num3)
                {
                    cout<<num1<<"+"<<num2<<"="<<num3<<endl;
                    resnum++;
                }
            }
            else
                dfs(t+1);
            b[i]=0;
        }
    } 
}
int main(){
    n=9; 
    dfs(1);
    cout<<resnum;
    return 0;
}