算法概论作业5.26 5.28 5.33

算法概论作业

5.26

以下是程序自动分析中的一个问题。对于一组变量x1,x2,…,xn,给定一些形如“xi=xj”的等式约束和形如“xi≠xj”的不等式约束这些约束能否同时满足？
例如，如下一组约束：x1=x2,x2=x3,x3=x4,x1≠x4，是无法同时满足的，请给出一个有效的算法，判断关于n个变量的m个约束是否可同时满足。

解题思路:

1.先处理相等约束，对相等的变量进行并集操作。
2.检查不等约束，
若不等号两边的变量位于同一个集合，则说明该约束条件是不可满足的，
若所有位于不等号两边的变量都位于不同集合中，即说明该约束条件是可满足的。

5.28

Alice想要举办一个舞会，为此需要决定邀请什么人参加。目前共有n个人可供选择， Alice根据他们之间是否相识列出了一个相互配对的列表。她希望邀请尽可能多的人参加，但同时必须考虑以下两点：在舞会上，每个人至少可以各找到5个相识和5个不相识的人。
请就此问题给出一个高效的算法，以n个人的列表及其相识配对列表为输入，输出最优的被邀请客人名单。并基于变量n估算其运行时间。

思路如下

1、建立无向图G(V,E)，并求出每个顶点的度
2、遍历所有顶点，若满足d(v)<5或者d(v)>6,则将顶点v放入一个待删除队列delete中
3、将待删除顶点删除，更新相关顶点的度，重复2 直至delete队列为空。

算法思路如下：

第一步，建立相识配对列表
第二步：遍历所有顶点，若满足d(v)<5或者d(v)>6,则将顶点v放入一个待删除队列delete
第三步：得出邀请名单

5.33

请说明如何实现一个关于公式长度为线性时间的Horn公式可满足性问题的吝啬算法。

首先读取所有的蕴含生成一张有向图：
对于每一个 Horn clause，将每一个左手边的 literal（后简称为 l-literal）连接到一个中间节点，并利用这个中间节点来记录这些l-literals 的个数，然后将中间节点连接到 r-literial（即右手边的 literal）。
例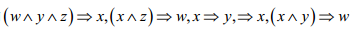以被表示为：

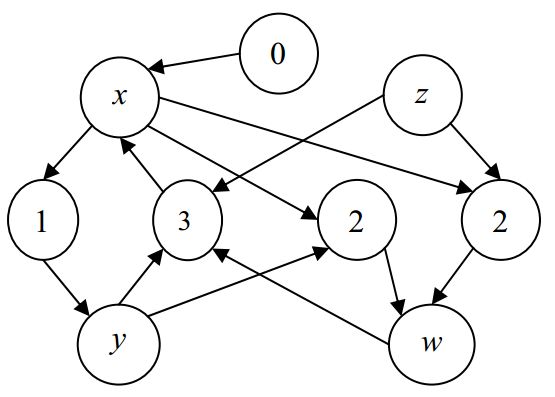
接下来先将所有 literals 的值设为 false ，
然后进行 DFS：从“0”节点出发，将它所连结的literal设为true，
同时将这个literal 所连的中间结点的值减 1，
如果有某个中间结点的值减1后为0，
则继续在这个结点上进行搜索，否则跳出。
DFS 过程结束后再对 negative clauses 进行验证即可。