奥里与属性克制(长郡csp模拟赛)

解题报告

题面大意

有一个元素为 0,1 的序列, 其中 1 的数量为 n, 0 的数量为 m.

一个人会对这个序列的每一位元素进行猜测, 在猜测后, 他会知道自己猜的对不对(也就是知道这个元素是什么).

在猜测的过程中, 他会根据已有的信息来进行最优决策.

求这个人猜对的元素个数的数学期望.

解题思路

以下思路均来自题解

首先, 这个"最优决策"指的是: 每次都猜测剩下更多的那个数.

然后, 这个不确定的序列可以用一个 nm 的网格图来表示

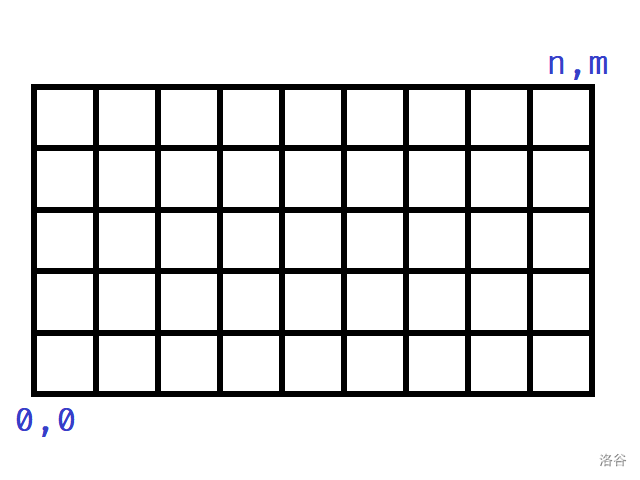
往上走一格, 当前位为 0,
往右走一个, 当前位为 1.
这样, 每一个序列都可以用唯一一条路径来表示.

设图上的点为 $(i,j), 0 \le i \le n, 0 \le j \le m$,
当 $i \not=j$ 时, 这个人猜测的下一个数都是固定的, 所以可以把每个序列的贡献标记为下图

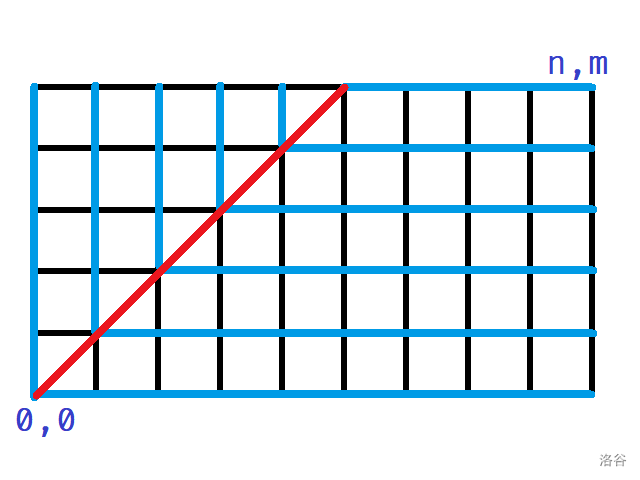
其中, 每经过一条蓝色的边就会得到 1 的贡献,

容易发现, 每个不同的序列都会经过 $n$ 条蓝边
也就是说, 这个人至少能猜中 $n$ 个数

所以, 如果忽略 $i=j$ 的点, 序列的总贡献就为 $n\cdot C(n+m,n)$,

当 $i=j$ 时, 这个人就会随便选一个点, 那么不管当前位是 0 还是 1, 都会有 0.5 的贡献.
所以, 我们只要算出点 $(i,i), 0 < i \le m$ 被经过了多少次, 乘上 0.5, 再加上前面的贡献, 就可以算出所有序列的总贡献,
那么再除上序列总数, 就可以算出期望了, 式子如下( $d$ 为点 $(i,i)$ 被经过的次数)

代码实现

#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
const int N=1000000+7;
const ll mod=998244353;
int ty,n,m;
ll fac[N],invf[N],ans,d;
ll q_pow(ll a,ll p){
    ll res=1;
    while(p){
        if(p&1) res=(res*a)%mod;
        p>>=1;
        a=(a*a)%mod;
    }
    return res;
}
ll inv(ll y){ return q_pow(y,mod-2)%mod; }
ll C(int n,int r){
    if(n==0||r==0) return 1;
    else return fac[n]*invf[r]%mod*invf[n-r]%mod;
}
void pre(){
    fac[0]=1;
    for(int i=1;i<=n+m;i++) fac[i]=(i*fac[i-1])%mod;
    invf[n+m]=inv(fac[n+m]);
    for(int i=n+m-1;i>=0;i--) invf[i]=invf[i+1]*(i+1)%mod;
    for(int i=1;i<=m;i++) d=(d+C(i+i,i)*C(n-i+m-i,m-i)%mod)%mod;
}
void get(){
    ll c=C(m+n,m);
    ans=(c*n%mod+inv(2)*d%mod)%mod;
    ans=ans*inv(c)%mod;
}
int main(){
    //freopen("type.in","r",stdin);
    cin>>ty>>n>>m;
    if(n<m) swap(n,m);
    pre();
    get();
    printf("%lld\n",ans);
    return 0;
}