homework_14真实的弦振动

计算物理
刘星辰

---

---

背景介绍

在一维的情况下，理想的弦振动方程为：

$$\frac{\partial^2y}{\partial t^2}=c^2\frac{\partial^2y}{\partial x^2}$$
实际的弦由于有刚度(stiffness)，而且波的传播过程中有摩擦损耗。其波动方程的形式有所变化。这里仅仅考虑弦刚度的影响，可以得到如下形式的波动方程。
$$\frac{\partial^2y}{\partial t^2}=c^2(\frac{\partial^2y}{\partial x^2}-\varepsilon L^2\frac{\partial^4y}{\partial x^4})$$
其中$\varepsilon$为无量纲的刚度系数，$L$为弦的长度。

---

刚度系数对振动情况的影响

计算程序
初始条件取为:

$$y=e^{-100(x-k)^2}$$
相关参数取值如下：
$$弦长度L=1.9m，波速c=250m/s，r=1/4$$

• 刚度系数$\varepsilon=3.8\times10^{-5},k=1.9/2$

不同时刻的振动情况：

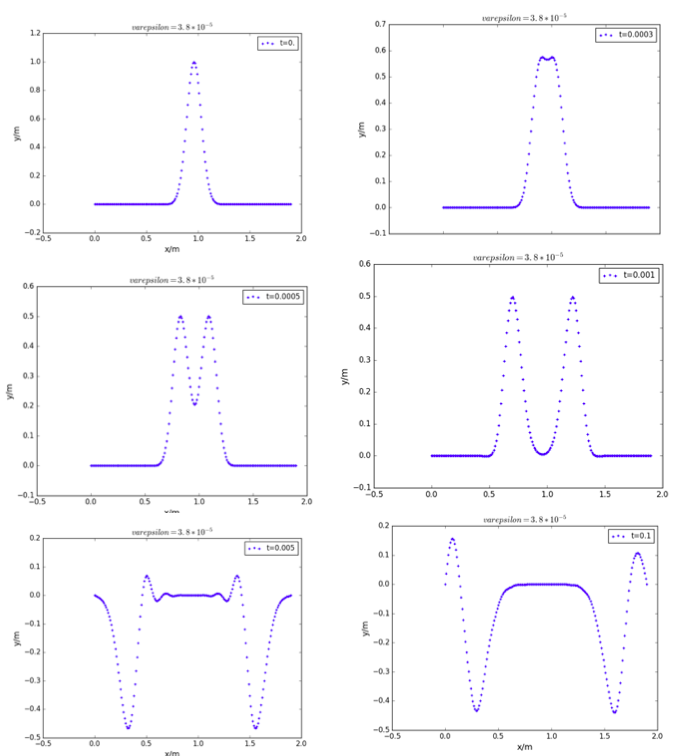
• 刚度系数$\varepsilon=3.8\times10^{-5},k=1.9/3$

不同时刻的振动情况：

• $k=1.9/2$

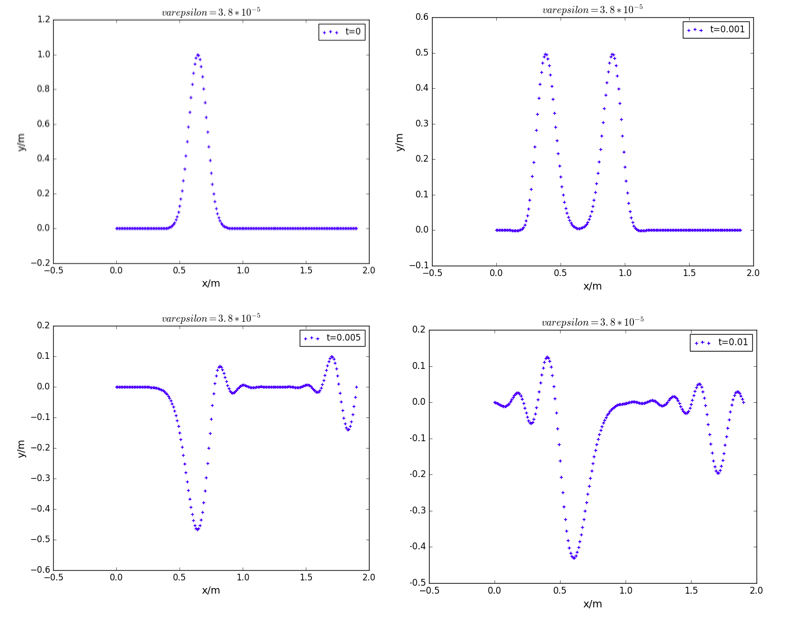
刚度系数取不同值时，$t=0.005$时刻的振动情况

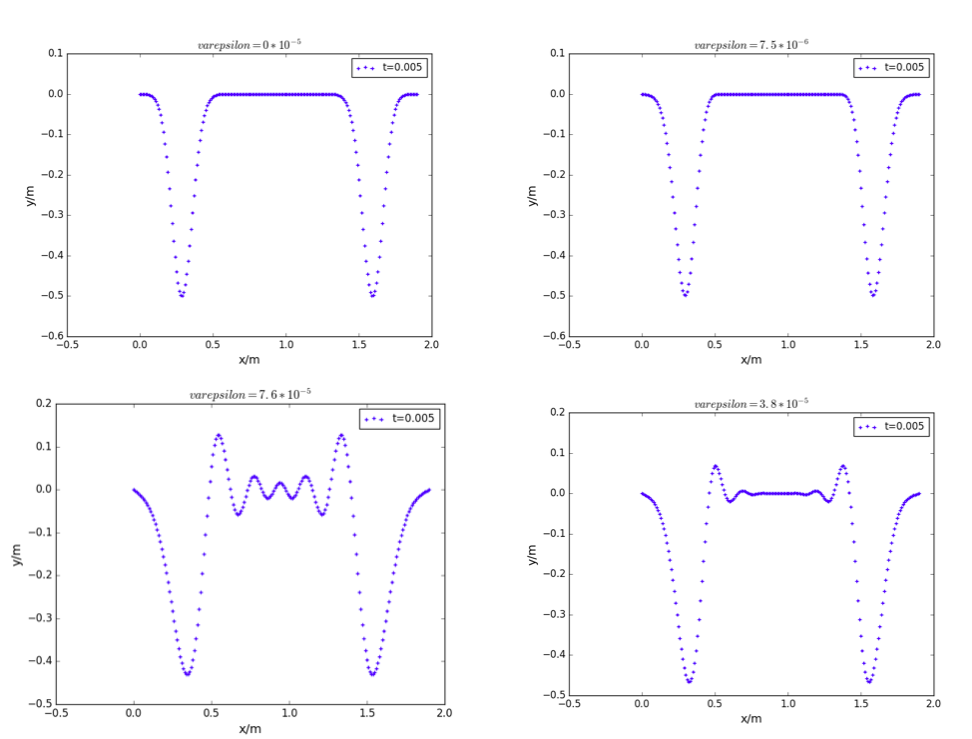
将初始条件改为：

$$y=sin\frac{2\cdot\pi(n+0.5)}{1.9}x$$
相关参数取值如下：
$$弦长度L=1.9m，波速c=250m/s，r=1/4$$

• 刚度系数$\varepsilon=3.8\times10^{-5},n=3$

不同时刻的振动情况

---

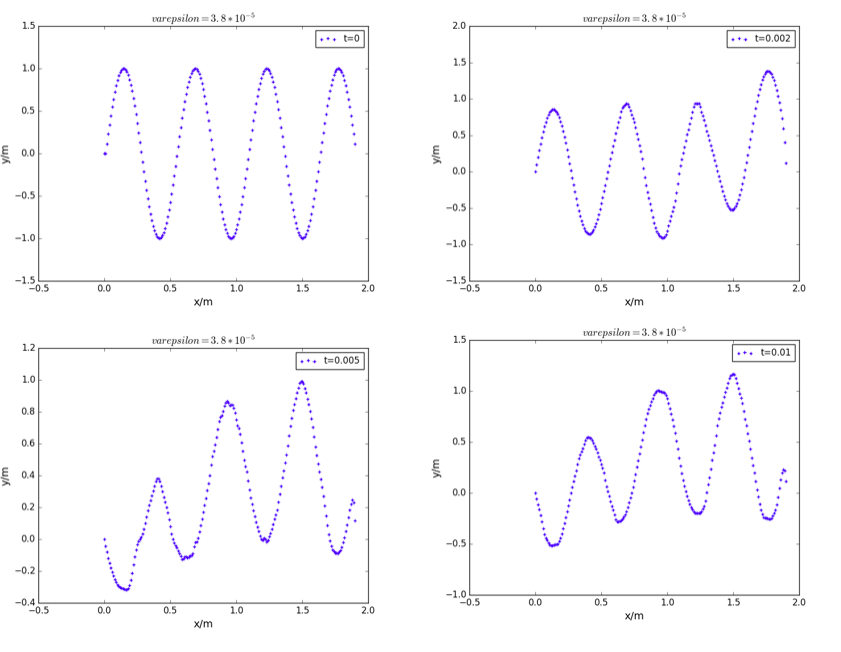
能量谱分析

初始条件取为:

$$y=e^{-100(x-k)^2}$$
相关参数取值如下：
$$弦长度L=1.9m，波速c=250m/s，r=1/4$$

• 刚度系数$\varepsilon=3.8\times10^{-5},k=1.9/2$

弦1/10处的能量谱（纵轴通过取对数单位转换为分贝）：

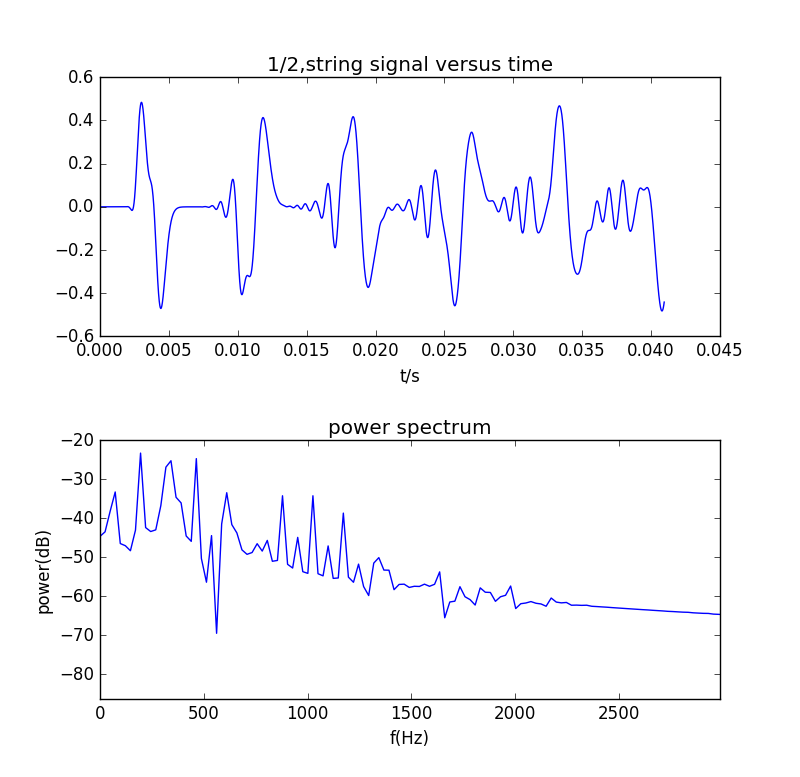
不考虑刚度时：

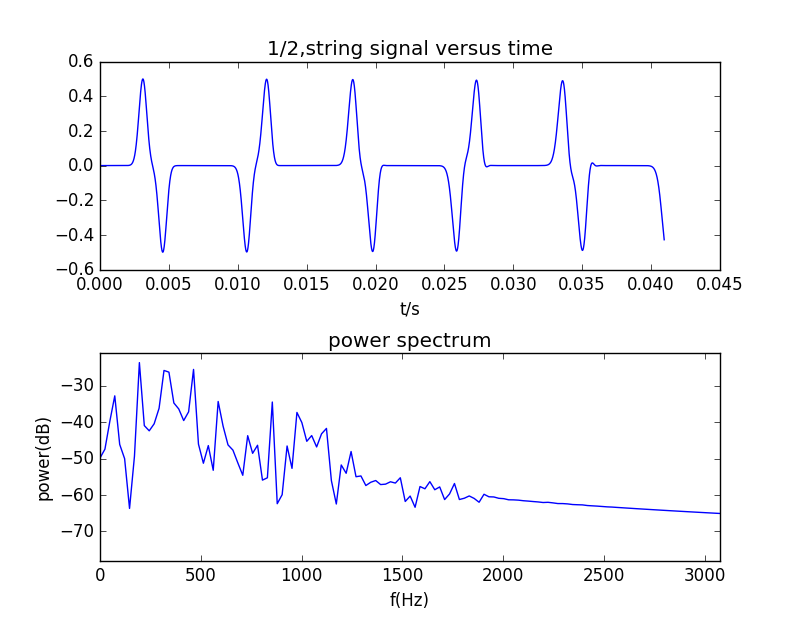
• 刚度系数$\varepsilon=3.8\times10^{-5},k=1.9/2$

弦中点处的能量谱（纵轴通过取对数单位转换为分贝）：

---

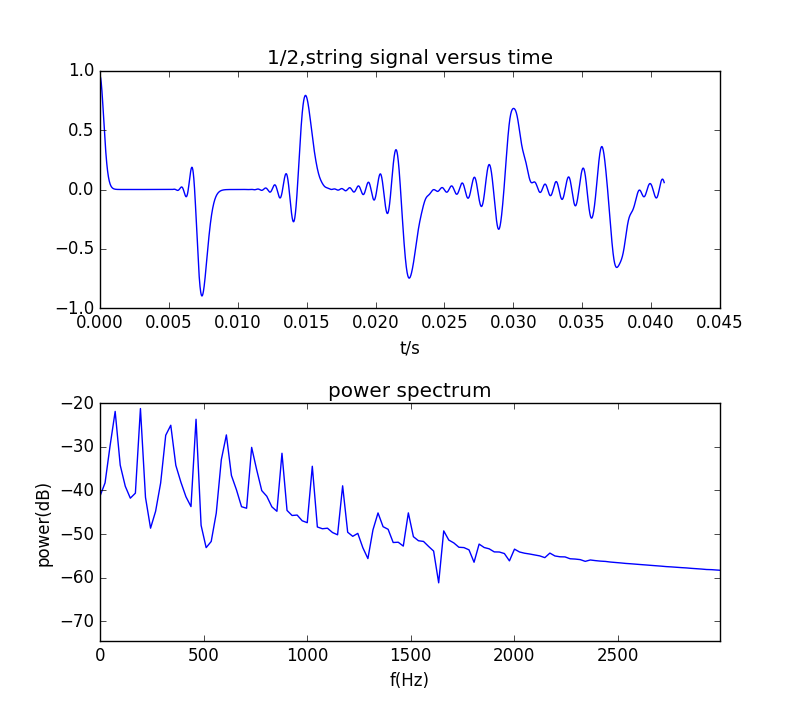
总结

考虑弦的刚度以后，初始条件为波包的情况下，弦的振动过程中会出现两个以上的波包，这在不考虑刚度时是不可能的。出现两个以上波包的原因在与方程中由四阶偏导项使得线性叠加原理失效。通过频谱的分析可以发现考虑刚度以后，弦振动的低频分量会增强。

---

参考文献

1. Computational Physics, Nicholas J. Giordano & Hisao Nakanishi
2. How to think like a computer scientist -- Learning with Python: Interactive Edition 2.0
3. Python图表绘制：matplotlib绘图库入门
4. latex数学符号表
5. 频域信号处理